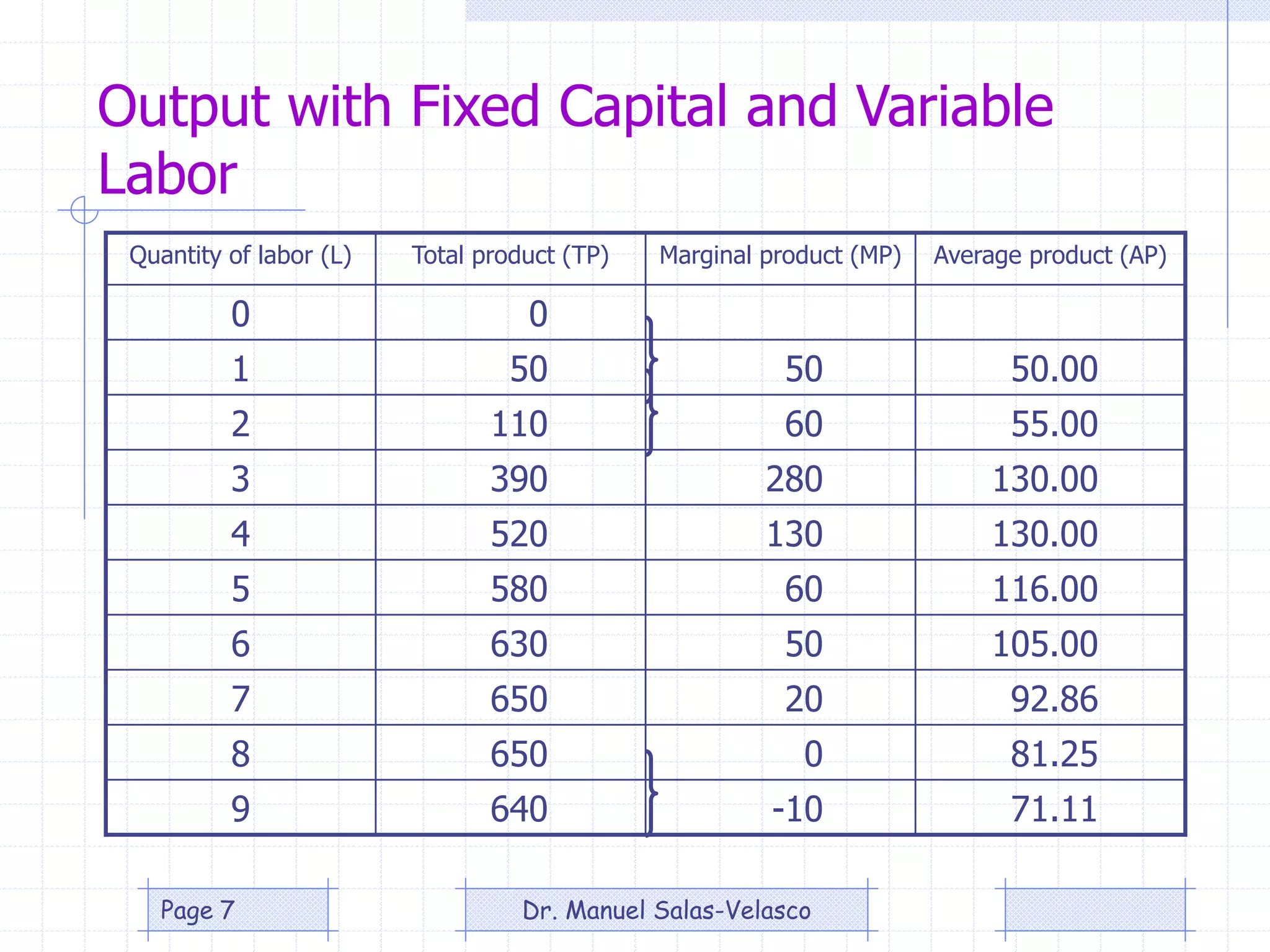
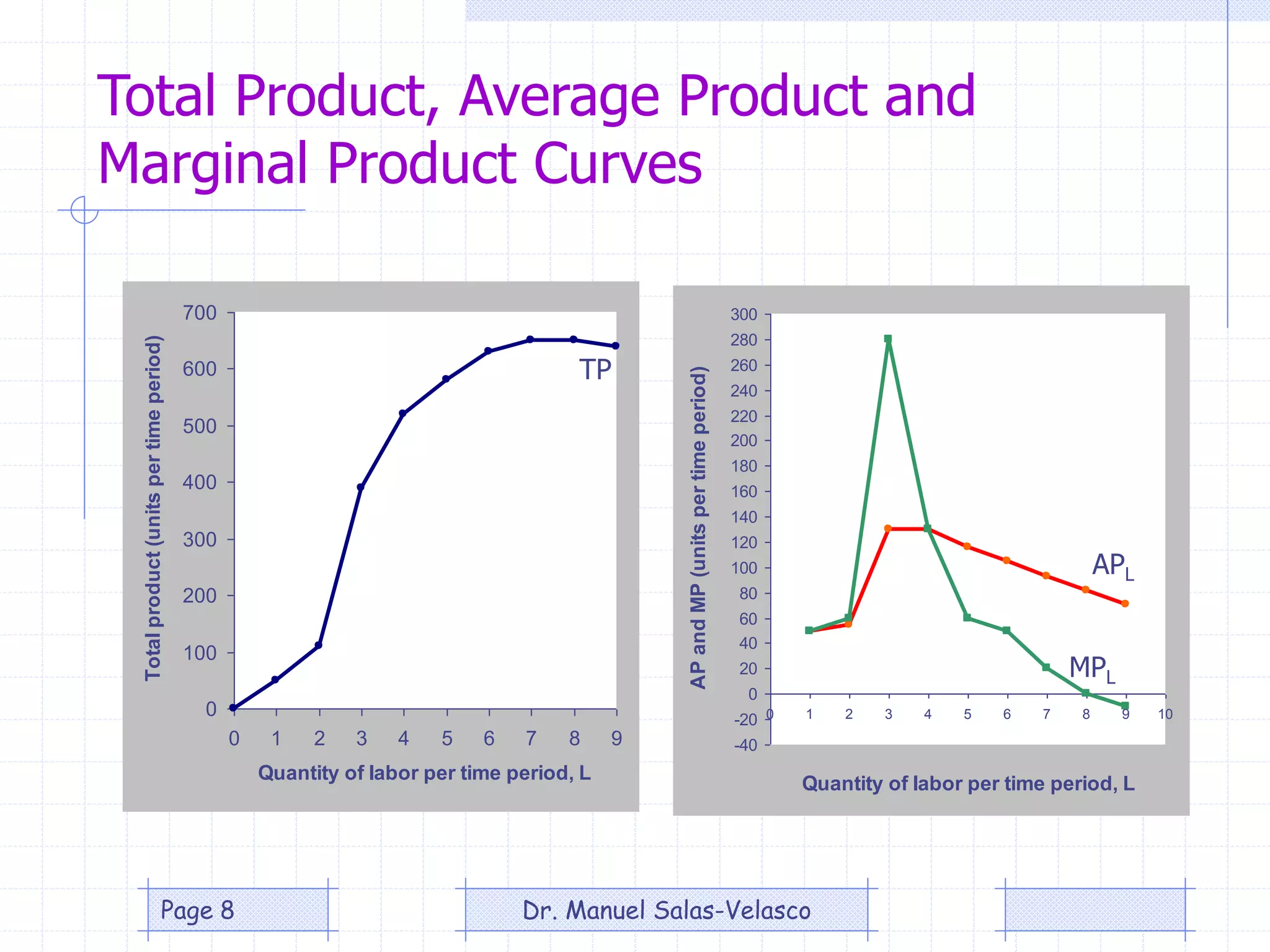
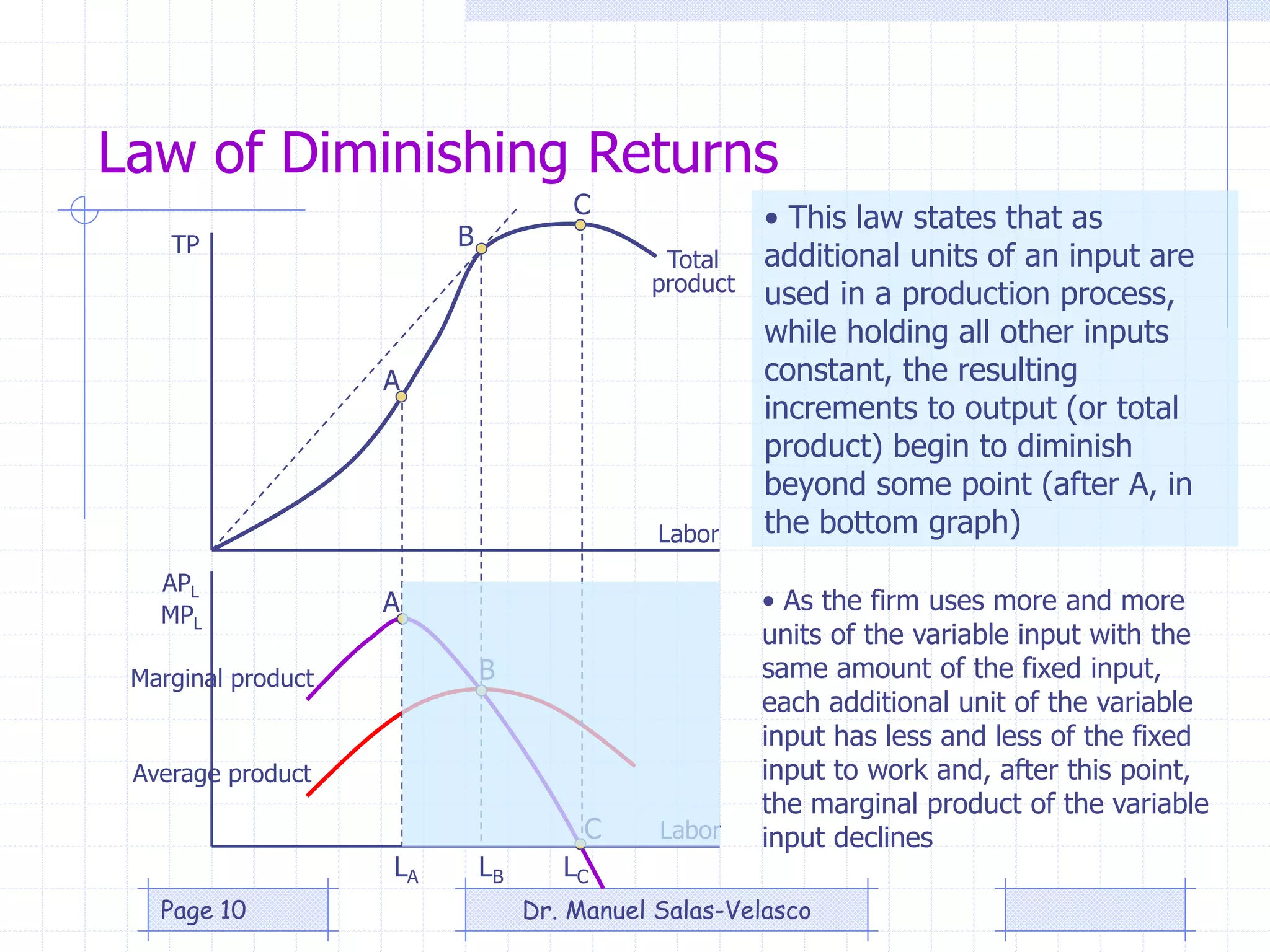
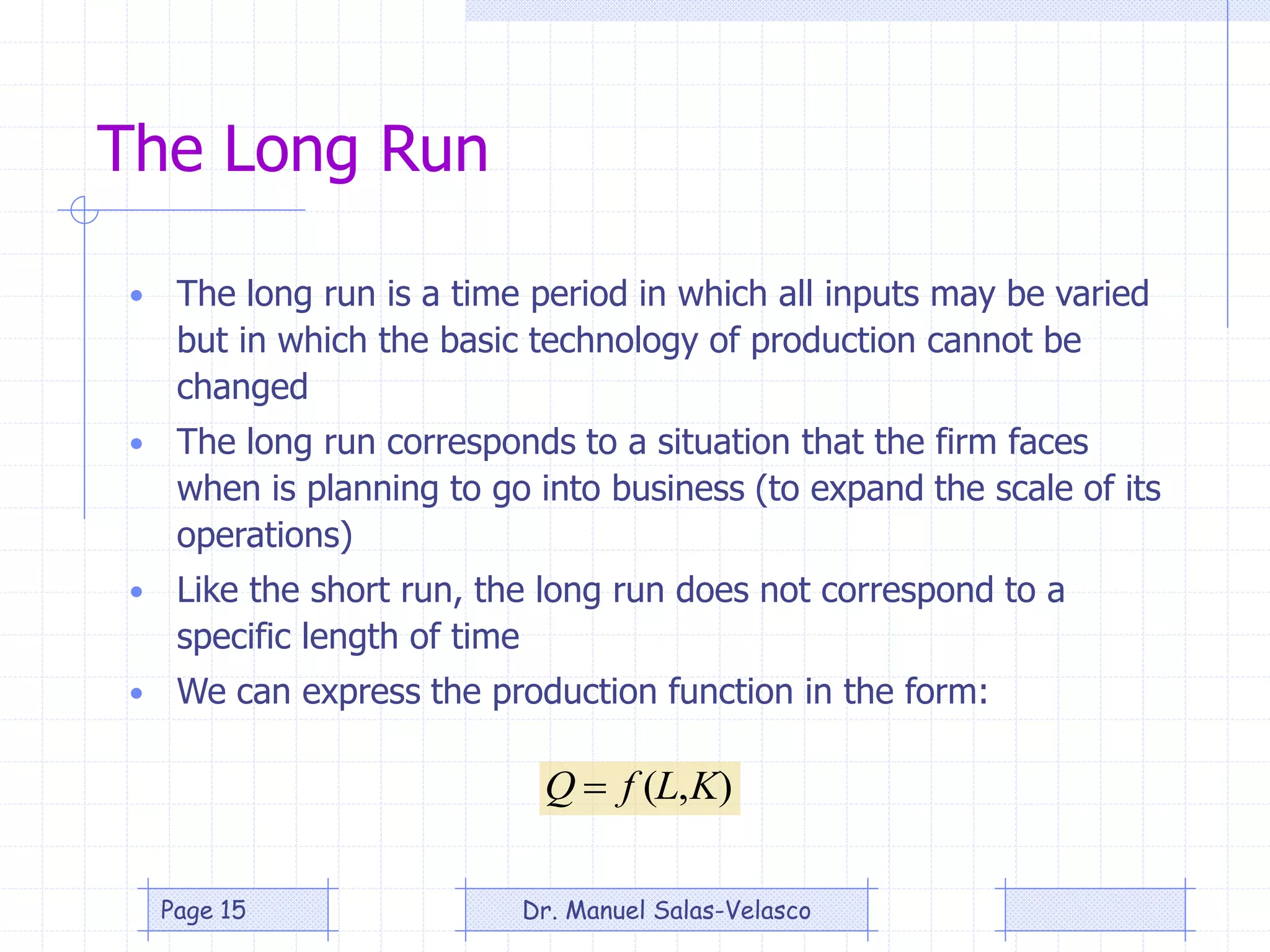
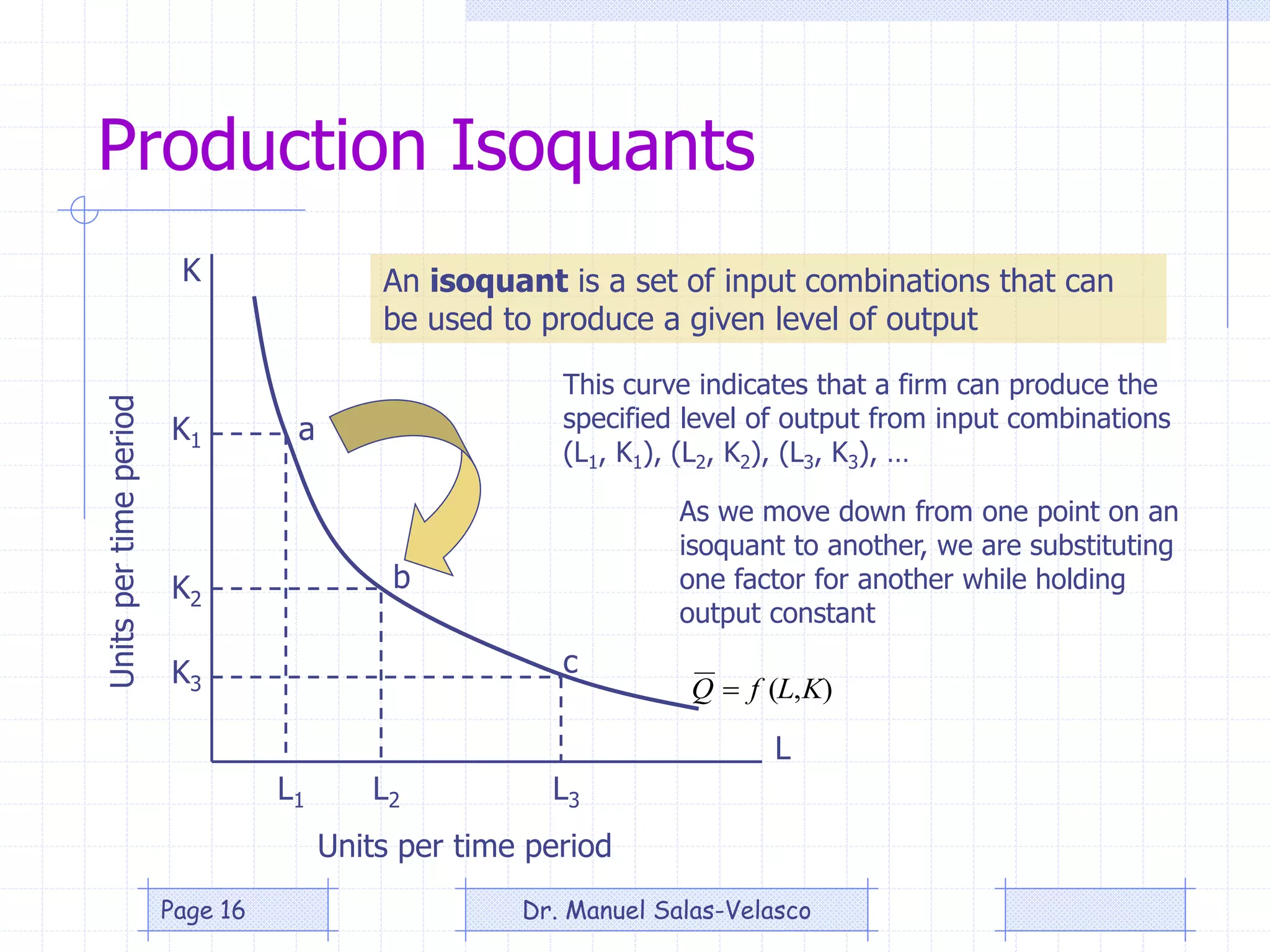
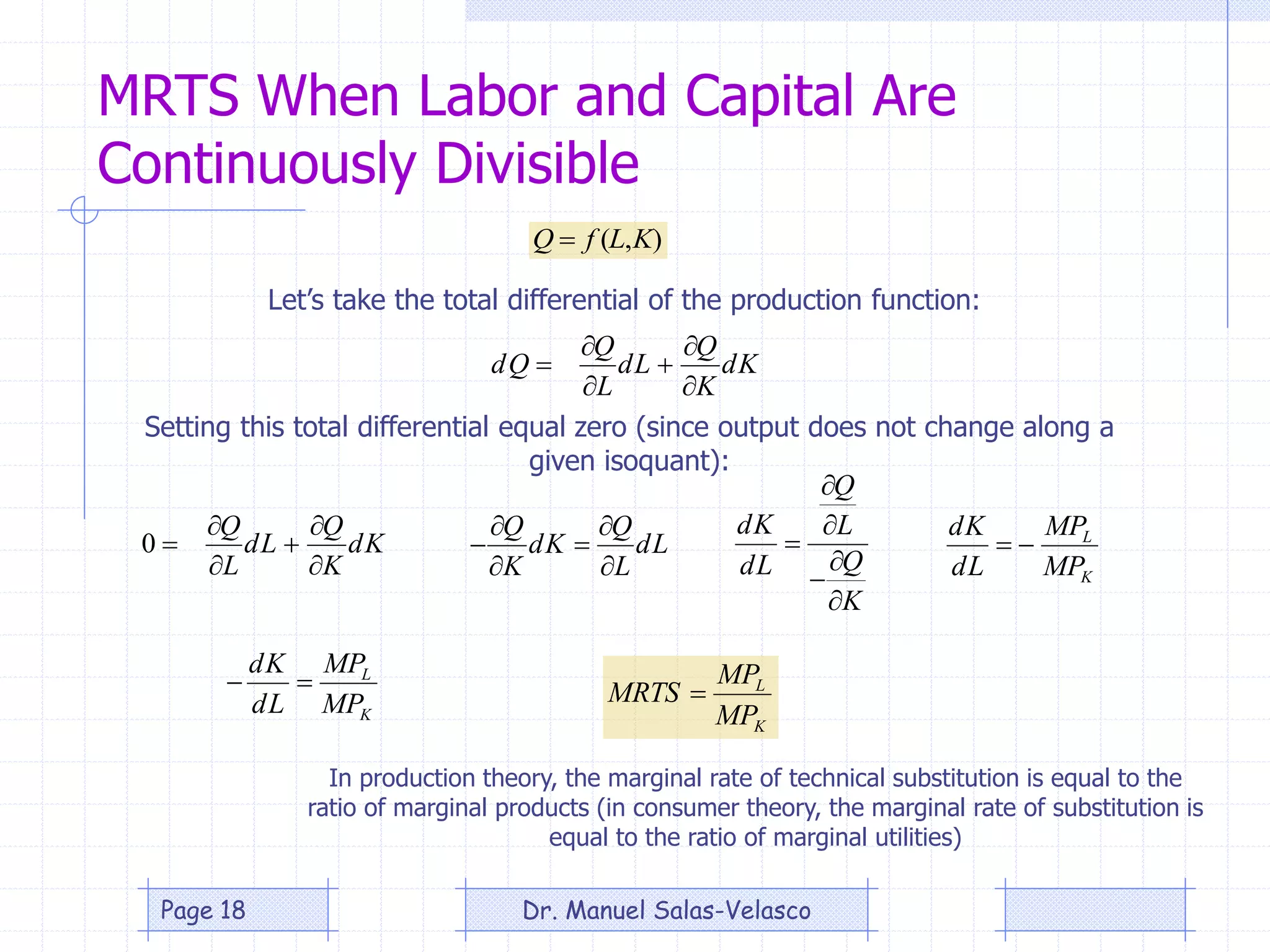
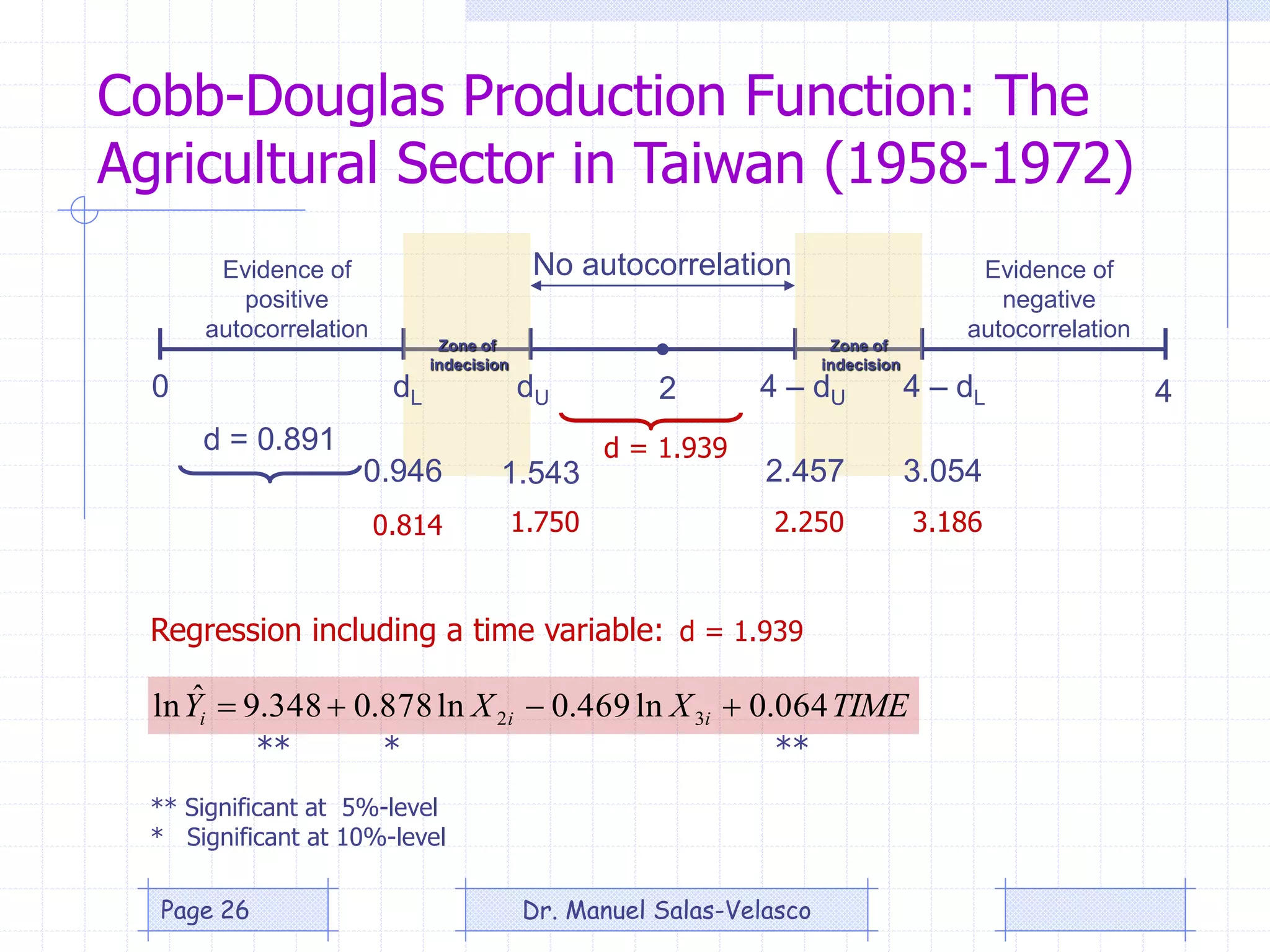
The document provides an overview of production theory, focusing on the production function which describes the relationship between inputs (labor and capital) and output. It discusses concepts like the short-run and long-run production, the law of diminishing returns, and the Cobb-Douglas production function, detailing how different variables affect production and efficiency. Additionally, it covers the econometric analysis of production functions, including the regression analysis challenges and methods to identify heteroscedasticity.