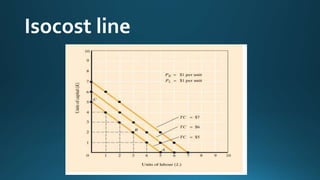
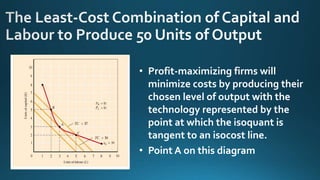
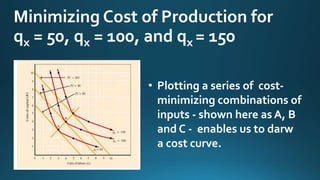
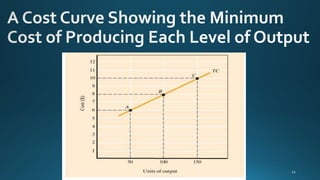
The document discusses isoquants and isocost curves. An isoquant shows the different combinations of two inputs, like labor and capital, that produce the same level of output. An isocost curve shows the combinations of inputs that can be purchased at a given total cost, given input prices. Together, isoquants and isocost curves can be used to find the cost-minimizing combination of inputs for a given level of output. The point where the isoquant is tangent to the isocost curve indicates the lowest cost combination.

1. Isocost Curve & Isoquant
Done by:
Hariharasudhan R
Divya Jothi

2. What is isoquant?
Isoquant is also called as equal product curve or
production indifference curve or constant product curve.
Isoquant indicates various combinations of two factors of
production which give the same level of output per unit
of time.

3. The significance of factors of productive resources is that,
any two factors are substitutable e.g. labor is
substitutable for capital and vice versa. No two factors
are perfect substitutes. This indicates that one factor can
be used a little more and other factor a little less, without
changing the level of output.

4. Assumptions
• There are two factor inputs labor and capital
• The proportions of factor are variable.
• Physical production conditions are given
• The state of technology remains constant

5. Isocost line
Isocost line shows various combinations of inputs that a
firm can purchase or hire at a given cost.
By the use of isocosts and isoquants, a firm can
determine the optimal input combination to maximize
profit.

6. It is a graphical representation of various combinations of
inputs say Labor(L) and capital (K) which give an equal
level of output per unit of time. Output produced by
different combinations of L and K is say, Q, then Q=f (L,
K).
A higher isoquant refers to a larger output, while a lower
isoquant refers to a smaller output.

7. Isocost line
Suppose a firm uses only labor and capital in production.
The total cost or expenditures of the firm can be
represented by:
C = wL + rK

8. Isocost line

9. • Slope of isoquant = - MPL / MPK
• Slope of isocost = - PL / PK
• For cost minimization we set these equal and rearrange to
obtain:
•

10. • Profit-maximizing firms will
minimize costs by producing their
chosen level of output with the
technology represented by the
point at which the isoquant is
tangent to an isocost line.
• Point A on this diagram

11. Minimizing Cost of Production for
qx = 50, qx = 100, and qx = 150
• Plotting a series of cost-minimizing
combinations of
inputs - shown here as A, B
and C - enables us to darw
a cost curve.