This document discusses axioms and their role in formal mathematical systems. It uses Euclid's geometry as an example, outlining his five axioms including the first axiom that there is exactly one straight line between any two points. Definitions are distinguished from axioms. Contradictions to axioms may indicate either a logical error or that a different mathematical system is being described. The document concludes by promising to discuss Euclid's fifth postulate in more depth.

1. Aim of this articleTo define what an axiom is.To give some perspective about axioms, definitions, and the sort.To give examples, and some explanations, mostly with respect to Euclid’s elements.Length: 17 slides

2. What is an axiom?

3. “An axiom is a logical statement that is assumed to be true”– Wikipedia

4. Why do we need axioms?As a basis for a “formal system”.

5. A framework to prove and/or derive further theorems.

6. Essentially, to enable ourselves to do math!Why do we need axioms?As a basis for a “formal system”.

7. A framework to prove and/or derive further theorems.

8. Essentially, to enable ourselves to do math!Axiomatic systems, are like the grammar and language rules for English. One needs those established, before one begins to write essays, or even make new words!Of course, rigor is of far greater importance in math, than in language.

9. Why do we need axioms?As a basis for a “formal system”.

10. A framework to prove and/or derive further theorems.

11. Essentially, to enable ourselves to do math!Due to their beauties, complexities, and other awesomeness, a full length discussion on formal systems is kept due for some time later.

12. What is an axiom? No. Really. What is it? It’s obviously not as simple as this?“An axiom is a logical statement that is assumed to be true”

13. What is an axiom? No. Really. What is it? It’s obviously not as simple as this?“An axiom is a logical statement that is assumed to be true”

14. What is an axiom? No. Really. What is it? It’s obviously not as simple as this?“An axiom is a logical statement that is assumed to be true”Or is it?

15. Okay…What does an axiom look like?Euclidean Geometry was one of the first formally defined axiomatic systems, complete and consistent in itself.That means, using all and only the 5 axioms Euclid used to define his system of geometry, you can prove all the results in geometry that do, or can ever, exist.

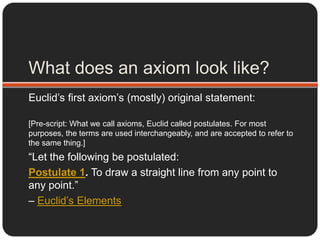
16. What does an axiom look like?Euclid’s first axiom’s (mostly) original statement:[Pre-script: What we call axioms, Euclid called postulates. For most purposes, the terms are used interchangeably, and are accepted to refer to the same thing.]“Let the following be postulated: Postulate 1. To draw a straight line from any point to any point.”– Euclid’s Elements

17. So, an axiom to tell us what a line is?An axiom does not rely on other axioms to be understood. Here, one should know that an axiom and a definition are distinct.Euclid defines:“A line is breadthless length.”And “A point is that which has no part.”

18. The line, the point, and definitionsThe definitions, in themselves, are (impressive) attempts, to provide us with a manifestation of the very abstract concepts of what a line and a point are, in the most vague and general form possible.They don’t have any consequence by themselves, and rely on language, for a comprehension of what is meant by breadth, length, and what a geometric figure, could have a ‘part’ of.

19. The line, the point, and definitionsThe definitions, in themselves, are (impressive) attempts, to provide us with a manifestation of the very abstract concepts of what a line and a point are, in the most vague and general form possible.They don’t have any consequence by themselves, and rely on language, for a comprehension of what is meant by breadth, length, and what a geometric figure, could have a ‘part’ of.Notice, that a line does not even require to be straight by definition!

20. So now, I don’t know what a point or a line is. What about that axiom?The axiom gives us some perspective about how Euclidean Geometry would work.In a more understandable language, the first axiom can be directly restated to say:“There will always be one line joining any two points. ”Something implicit in our experiences so far, and something Euclid chose to not say here explicitly, can be worded as:“One and only one straight line passes through two distinct points.”

21. Why then, must I care about definitions?Definitions are valid across systems.So when one uses a certain term, and clearly violates an axiom we are aware of, either we are faced with a contradiction, or a statement belonging to another system.

22. A contradiction, from outer spaceFor instance:There may be pairs of points through which an infinitude of lines go.This statement is in direct contradiction with Euclid’s First Axiom, especially as rephrased, before.

23. A contradiction, from outer spaceFor instance:There may be pairs of points through which an infinitude of lines go.This statement is in direct contradiction with Euclid’s First Axiom, especially as rephrased, before.“One and only one straight line passes through two distinct points.”

24. A contradiction, from outer space!For instance:There may be pairs of points through which an infinitude of lines go.This statement is in direct contradiction with Euclid’s First Axiom, especially as rephrased, before.“One and only one straight line passes through two distinct points.”

25. A contradiction, from outer spaceThis is possible in two cases:You just did something wrong, to reach that conclusion.You’re working in another system of geometry. The second conclusion can only be made, when one is sure what the words ‘point’ and ‘line’ mean. Which are independent of the system we are talking with regard to.