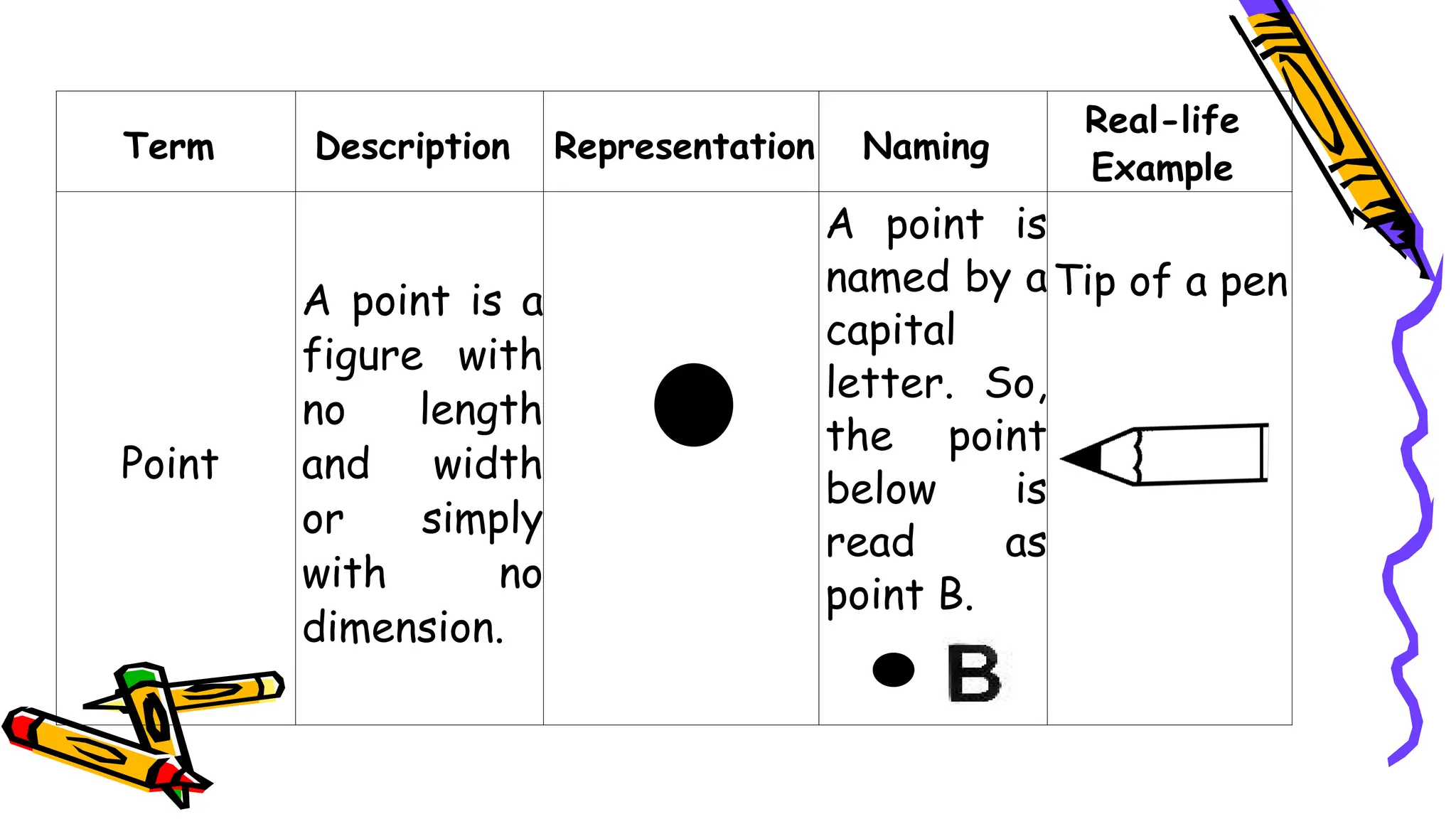
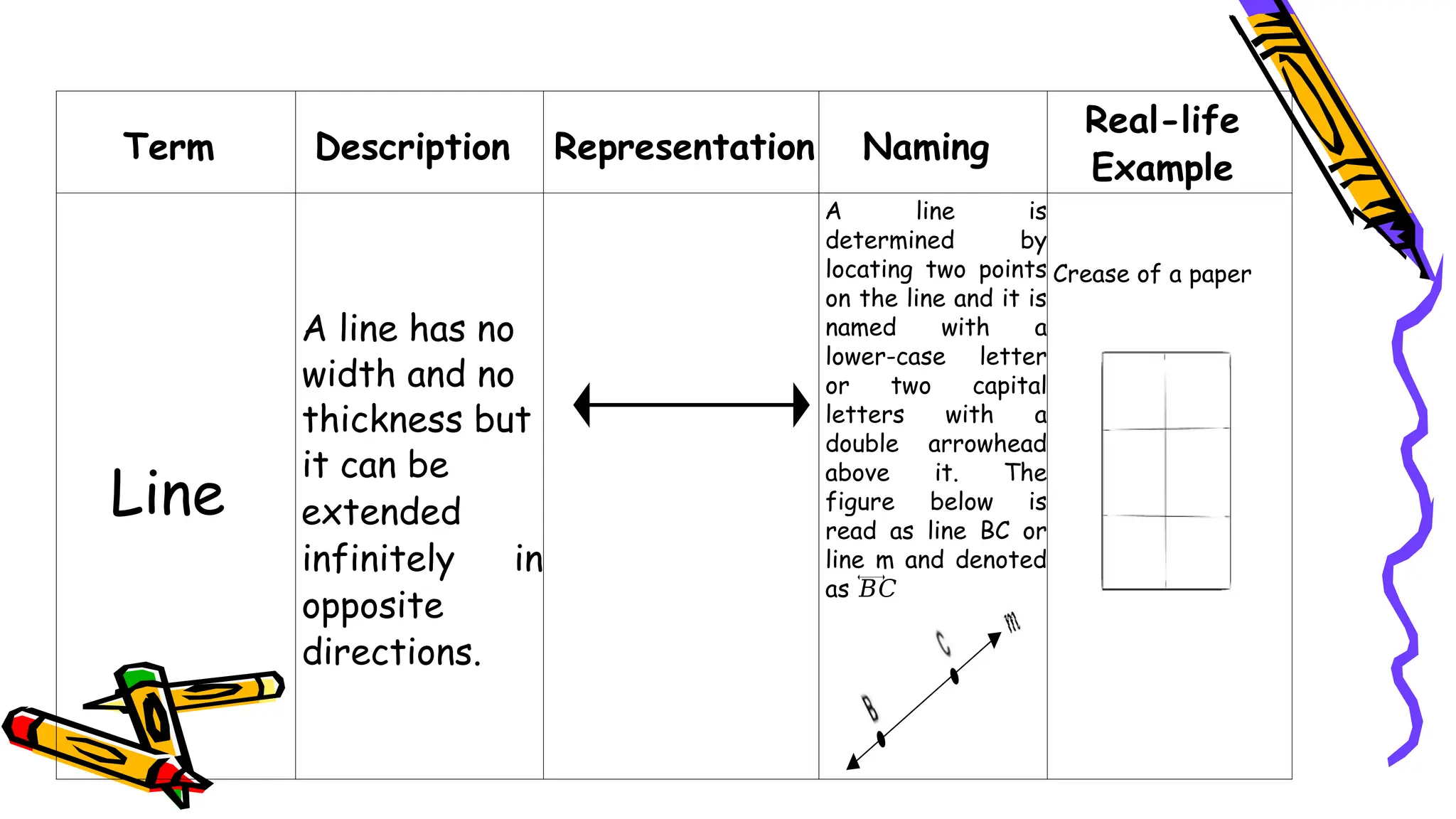
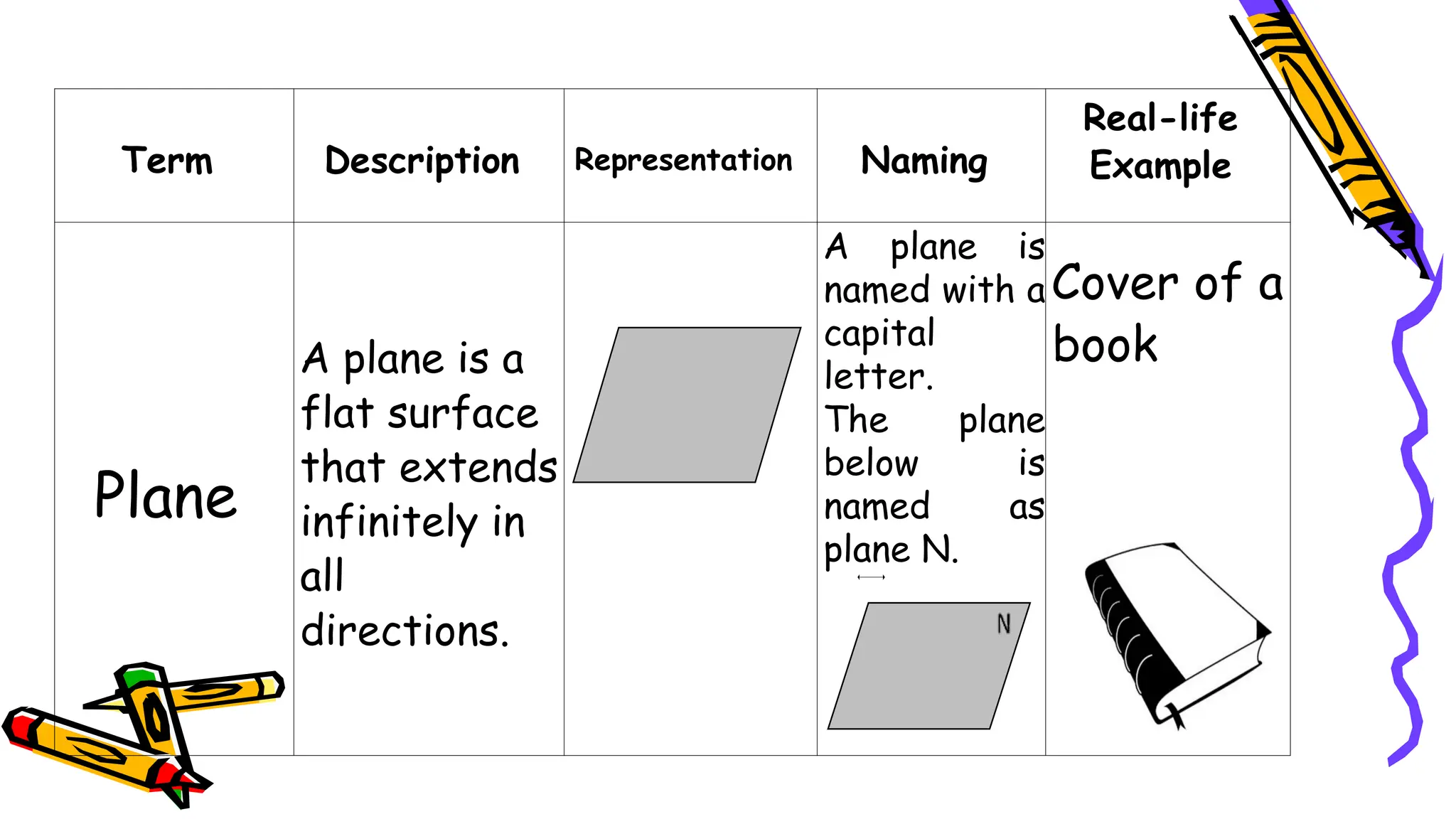
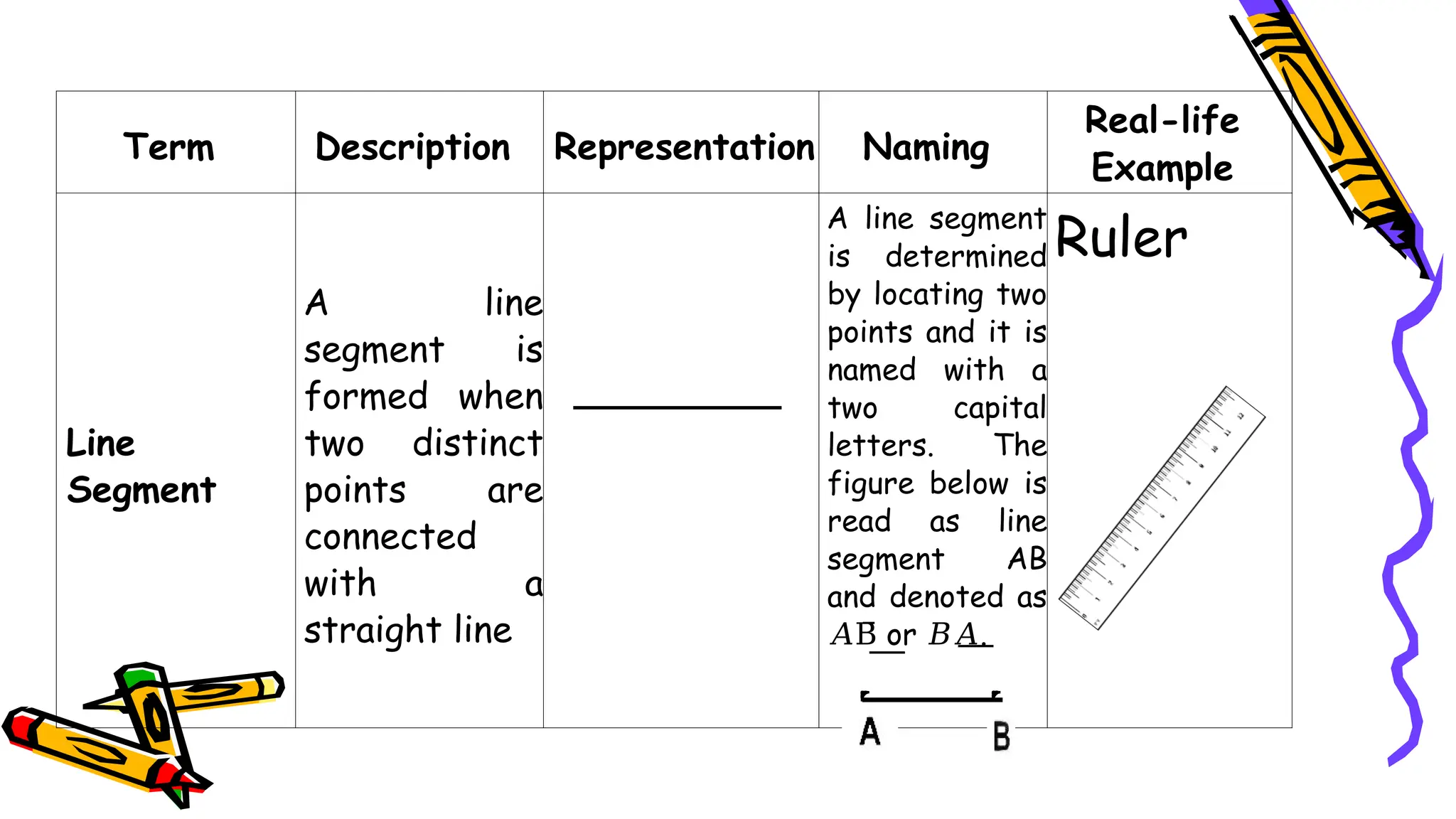
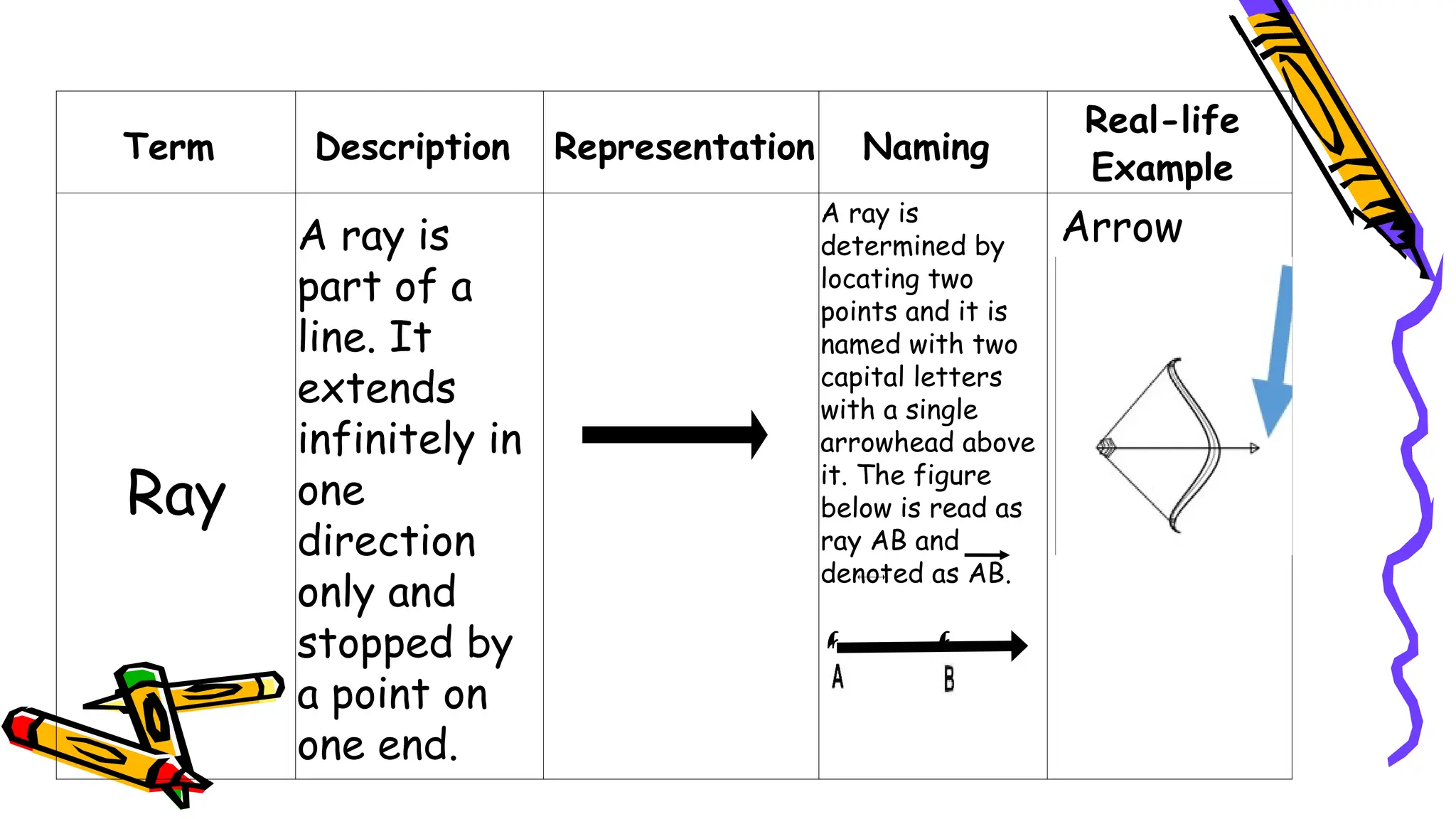
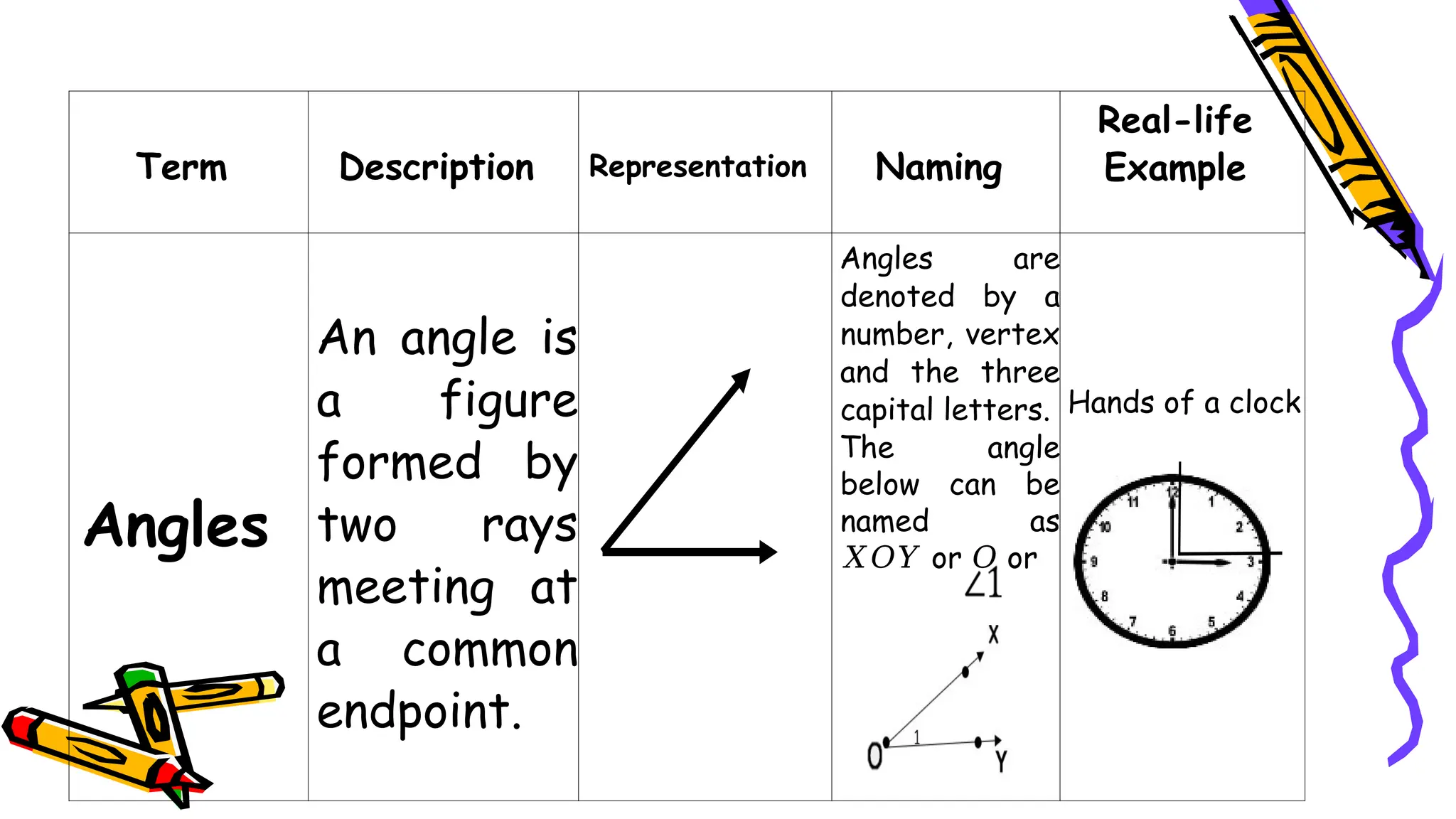
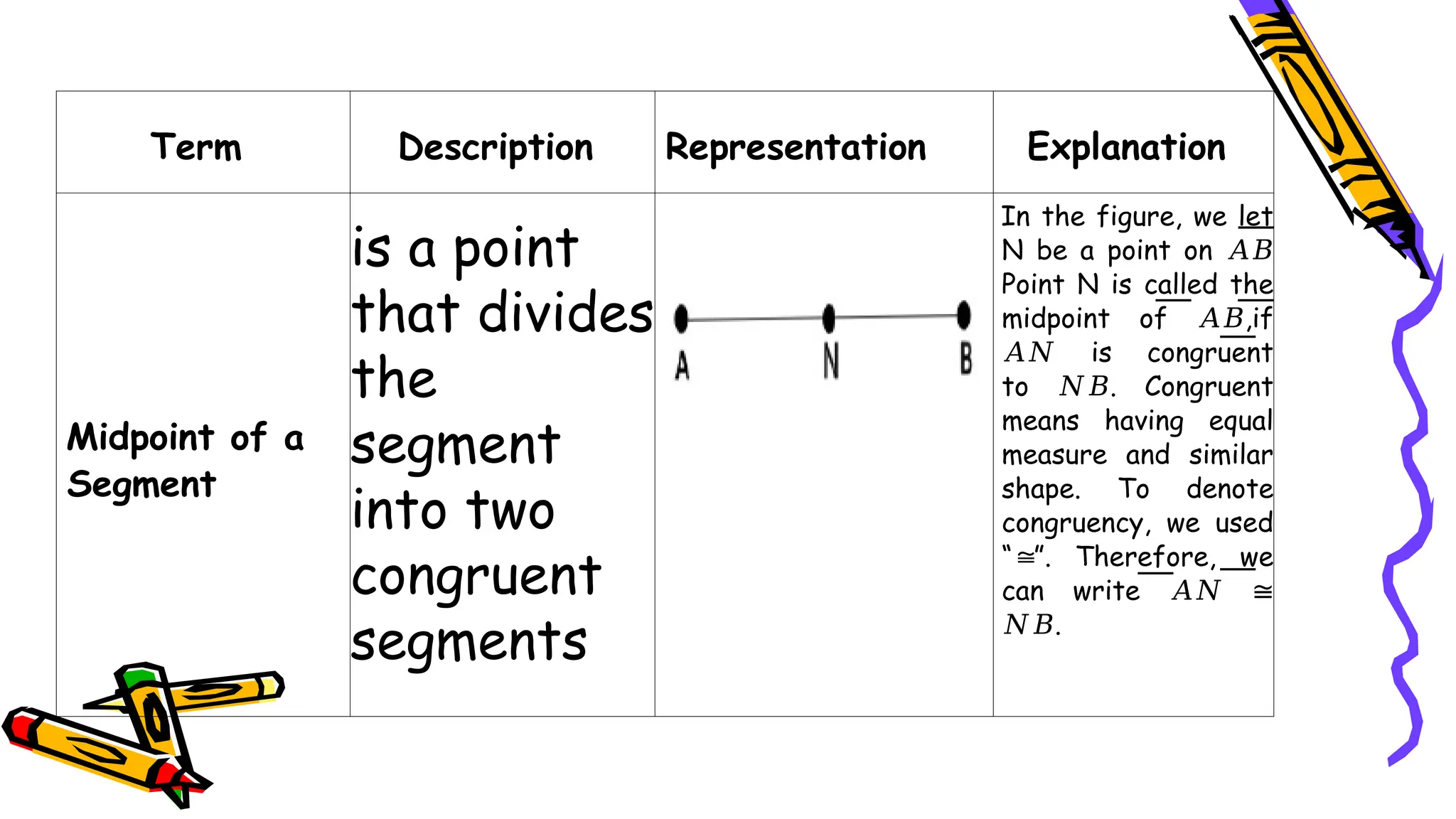
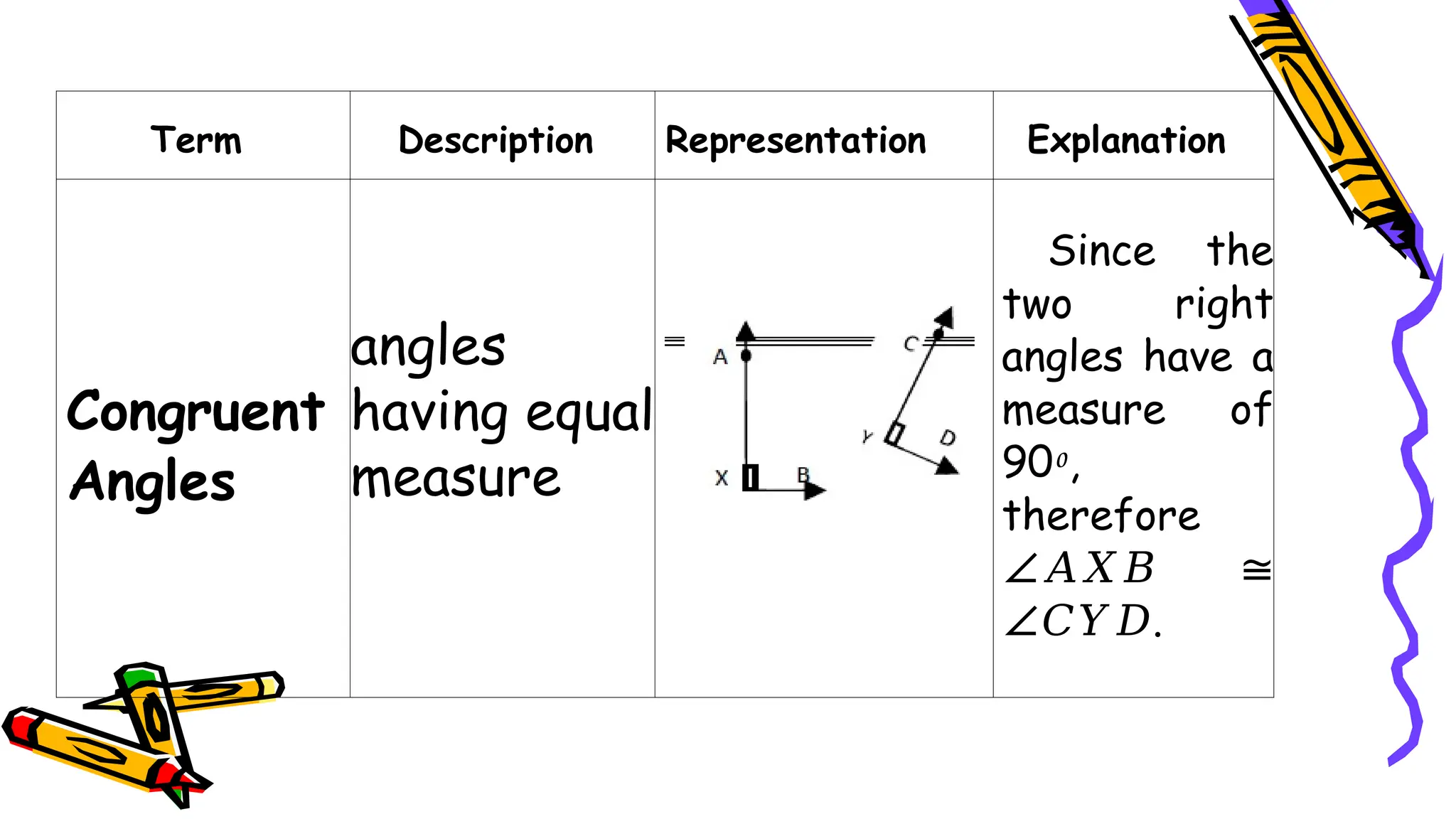
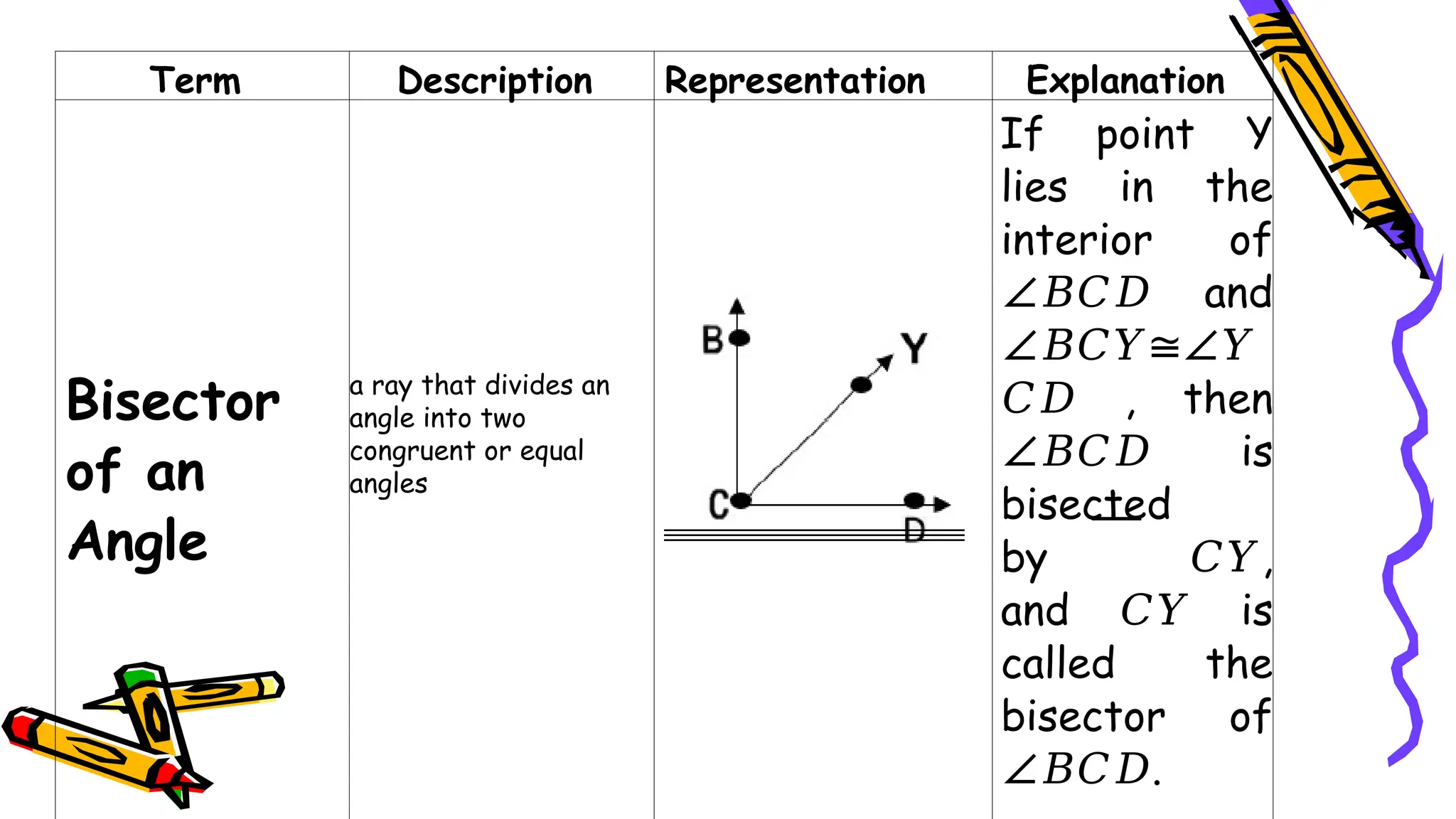
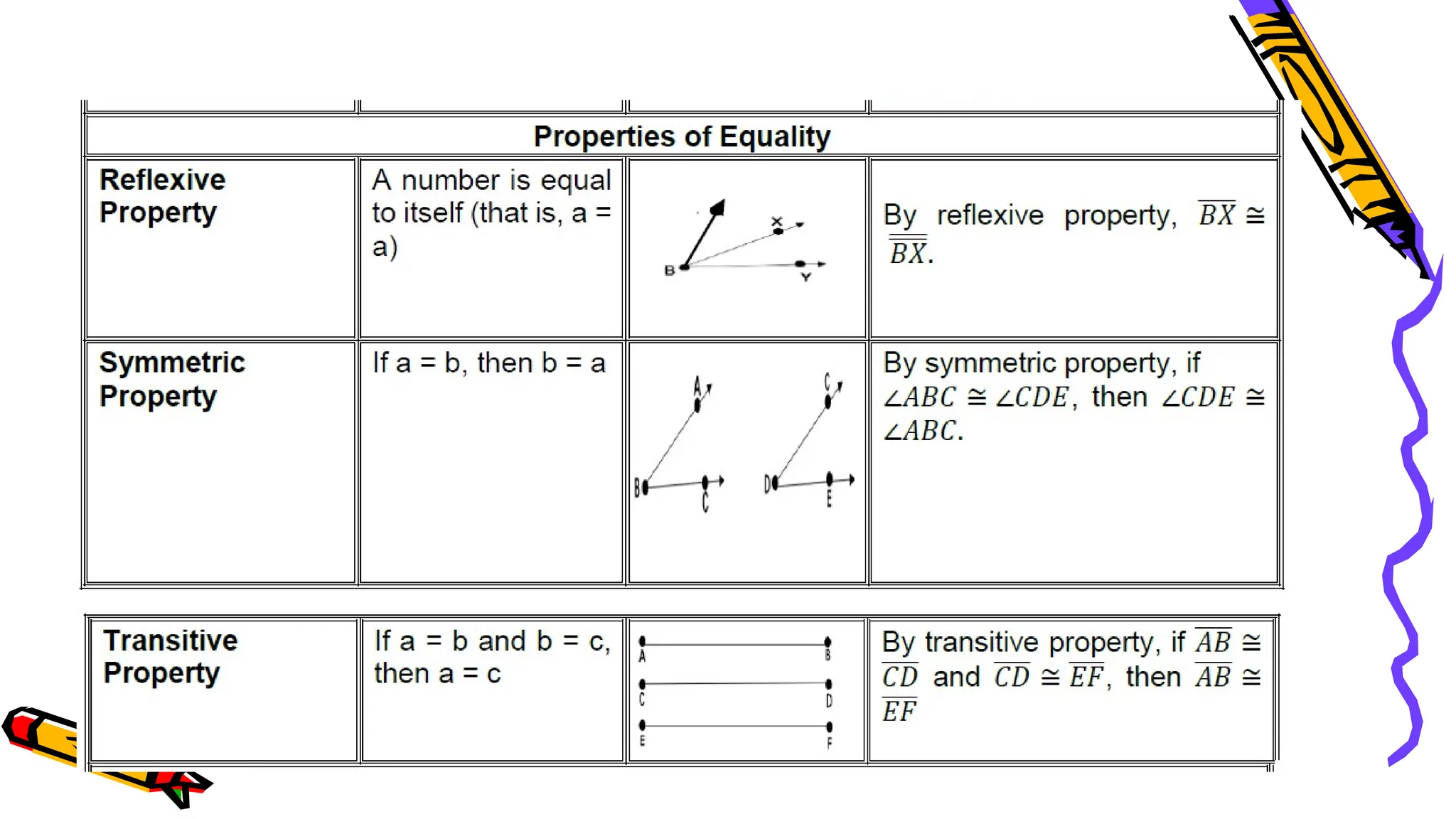
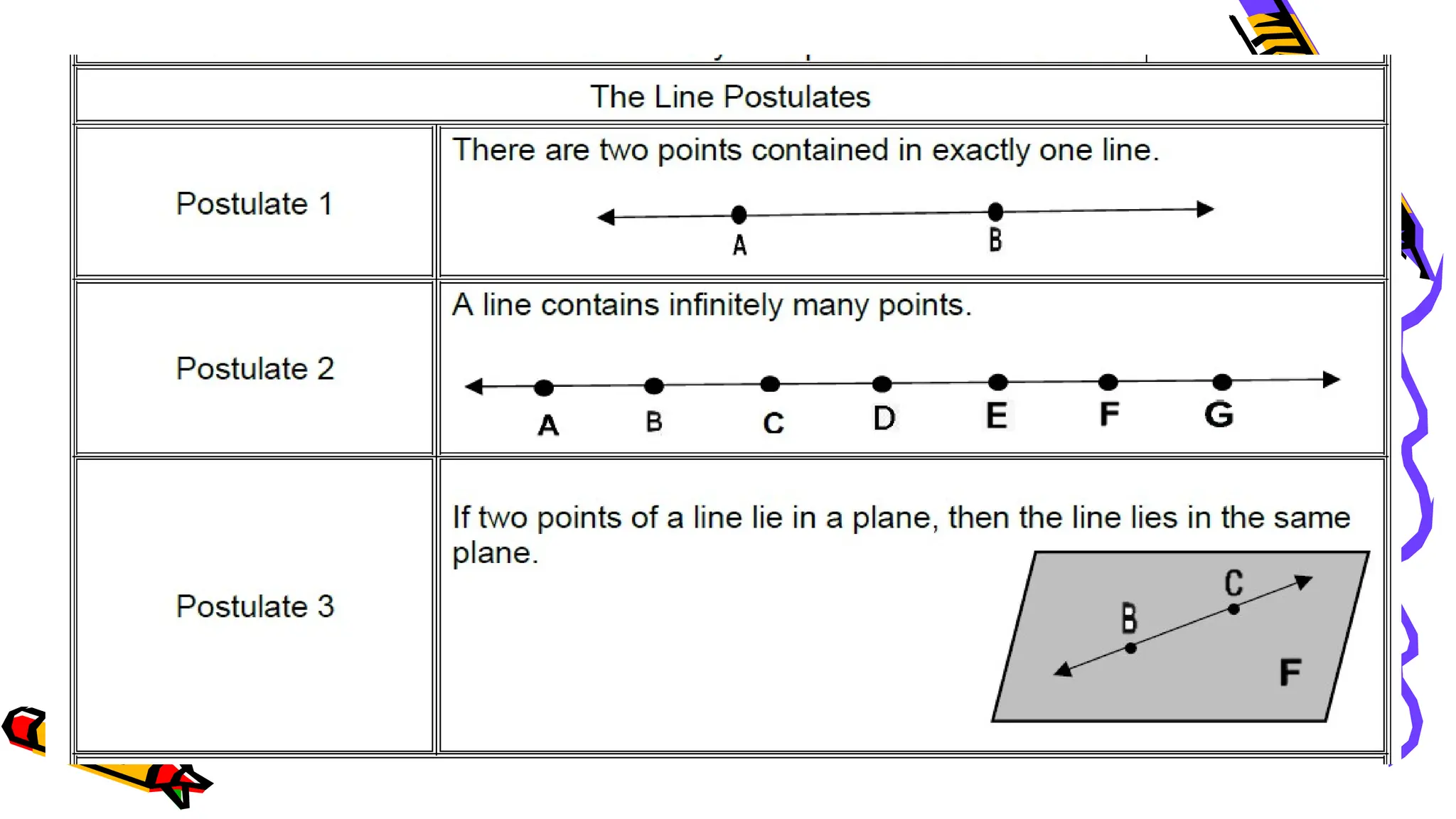
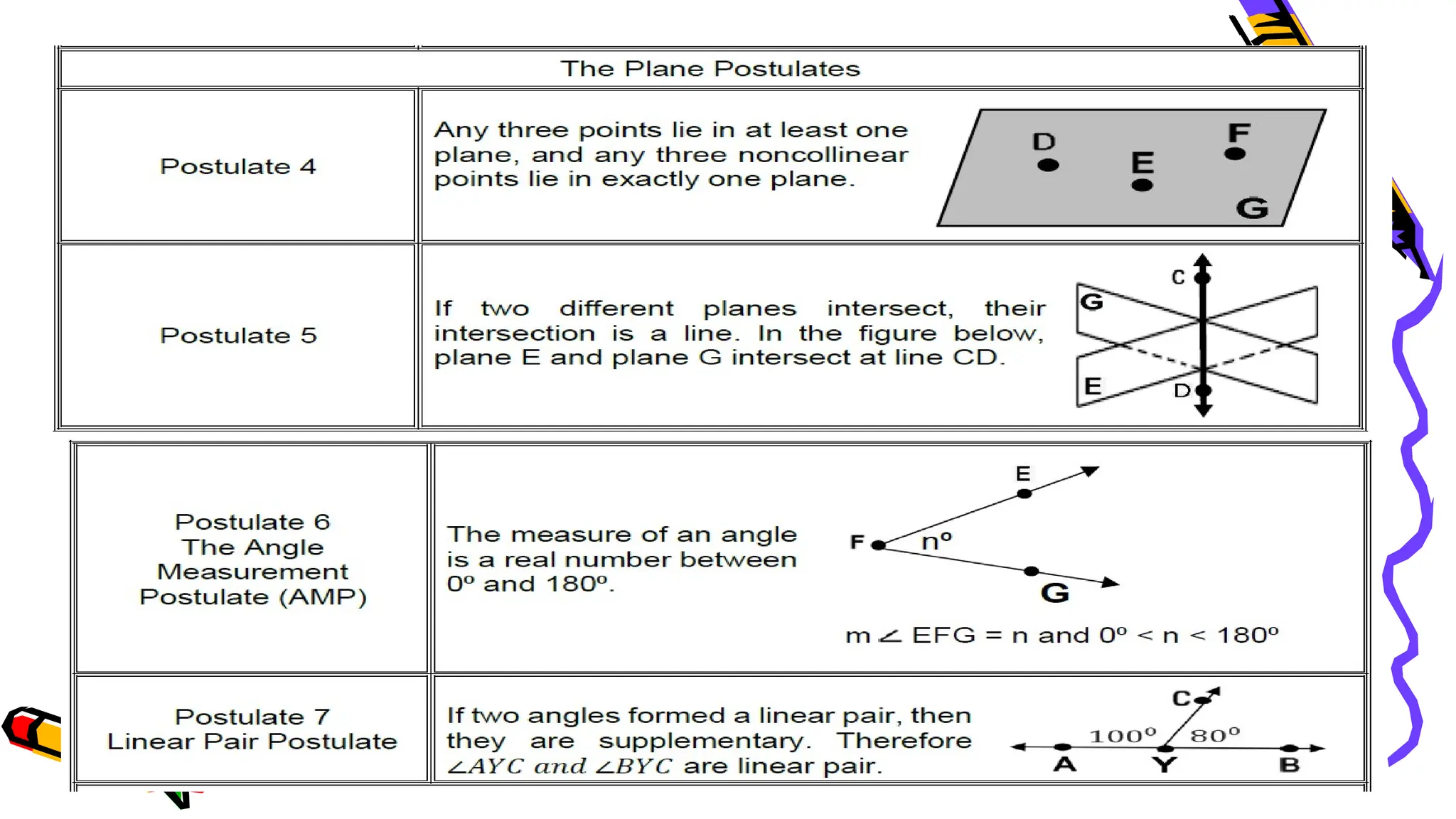
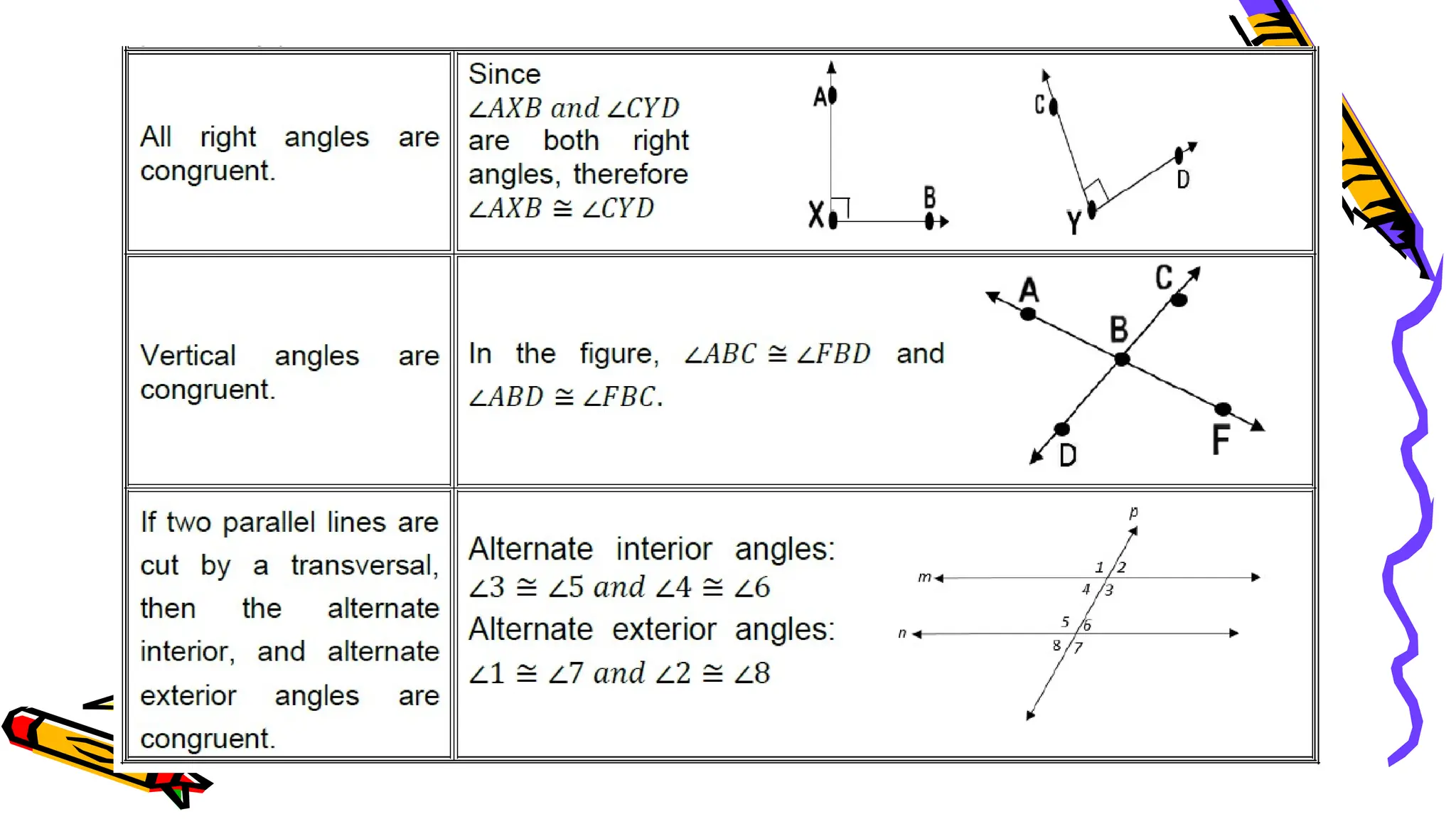
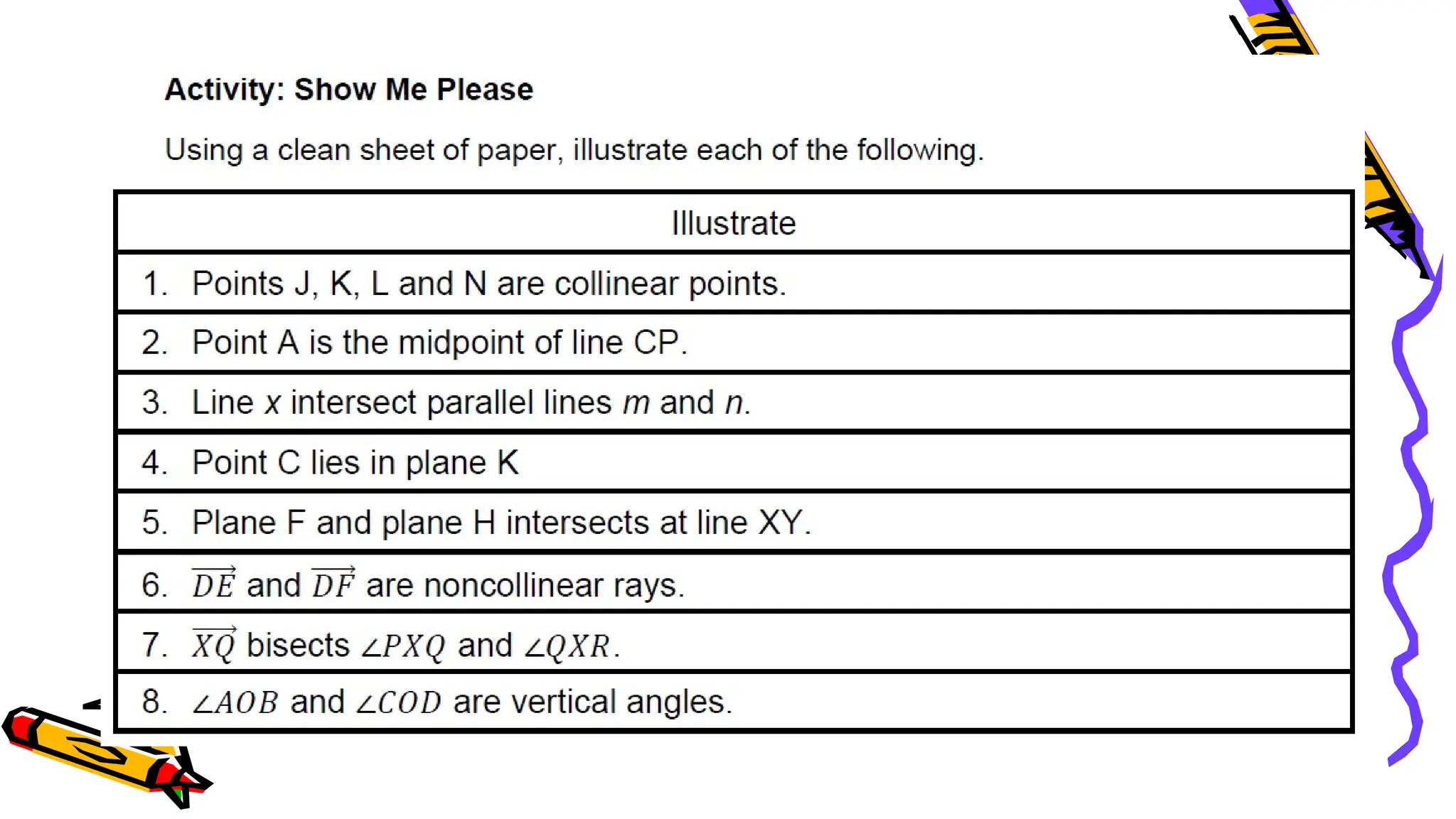
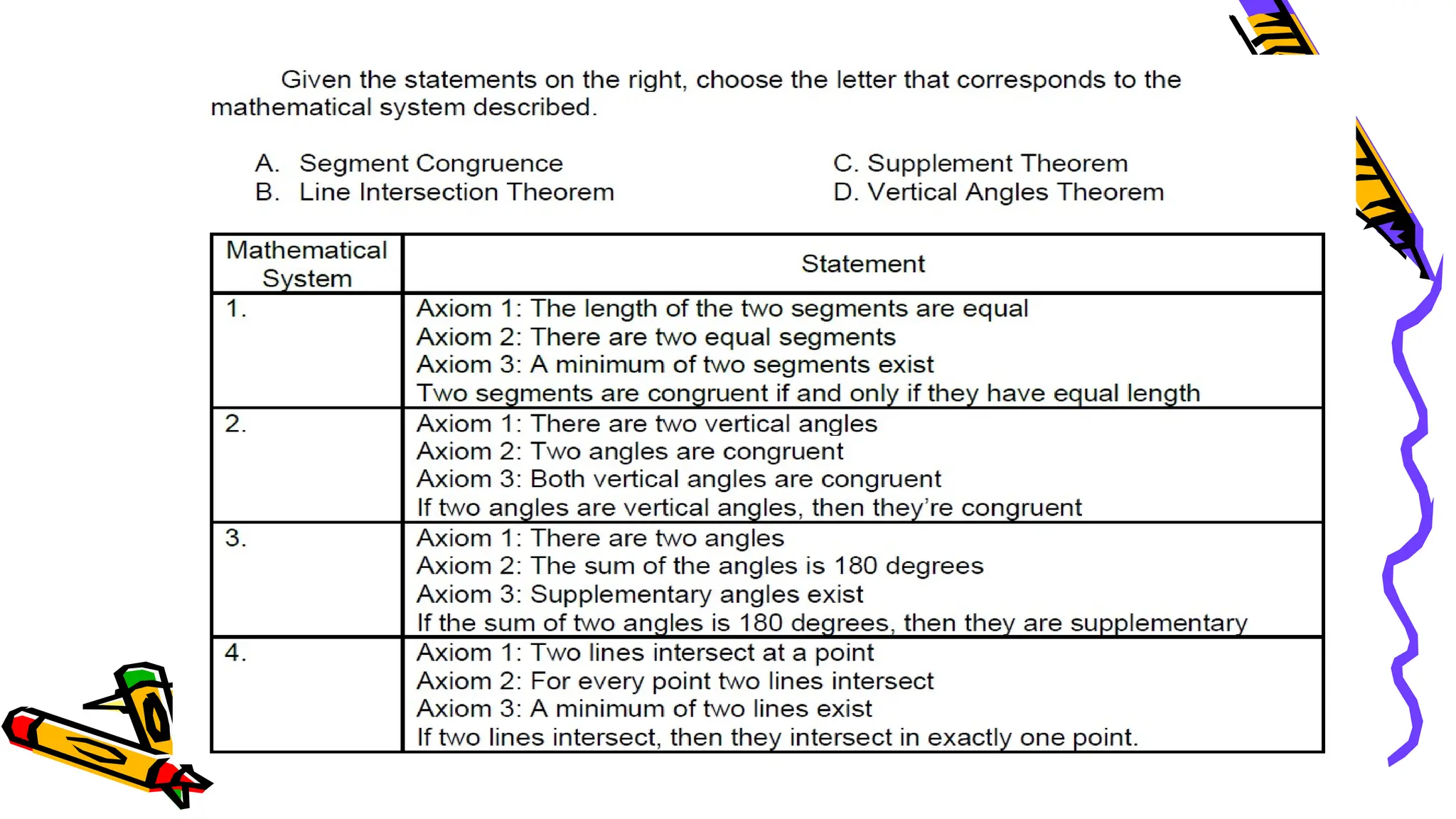
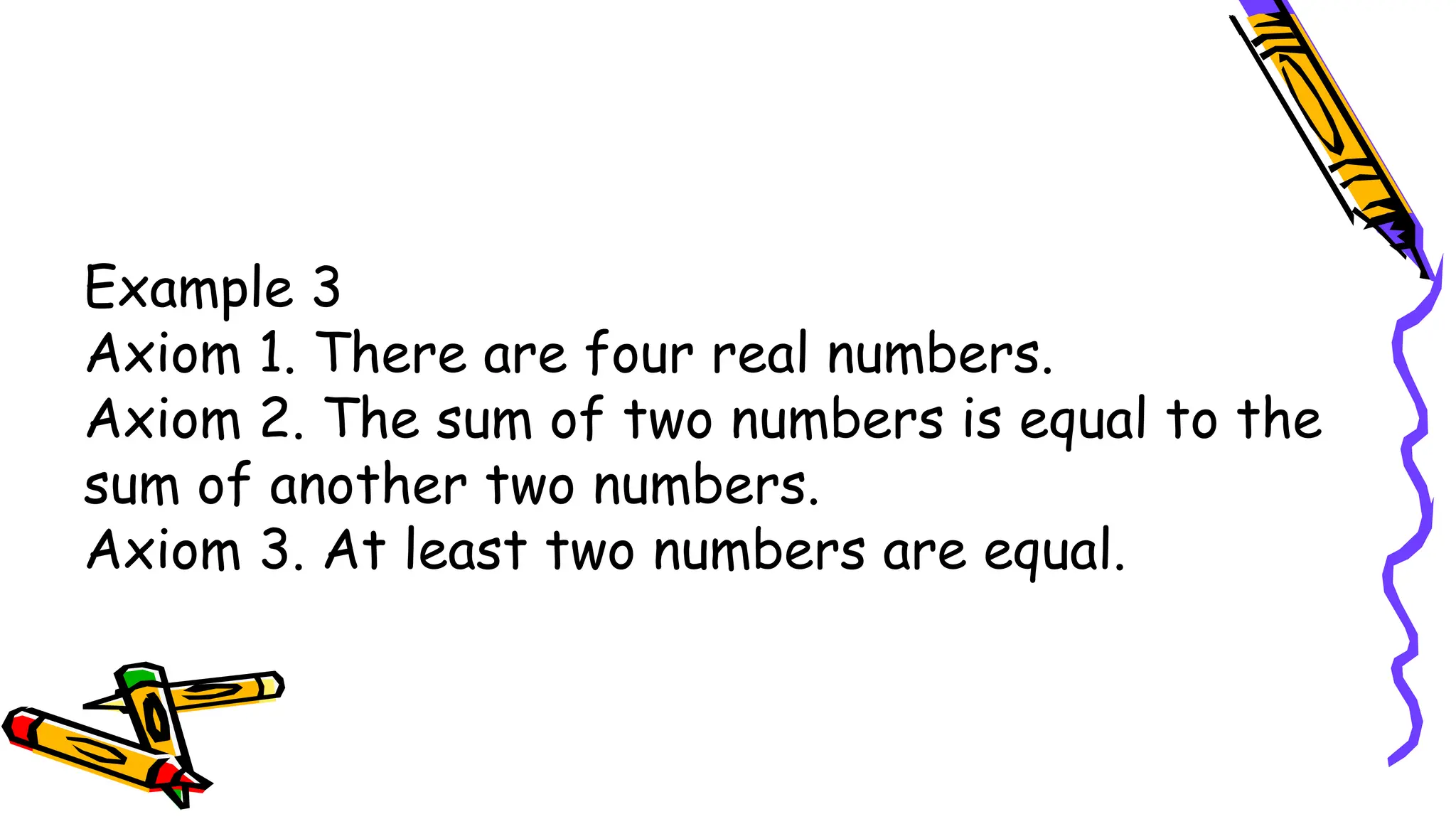The document outlines a mathematics activity focused on understanding basic geometric concepts, including undefined and defined terms, axioms, postulates, and theorems. It includes various activities such as multiple-choice questions, word jumbles, and real-life examples to illustrate points, lines, planes, and angles. The content emphasizes the importance of a systematic approach in geometry, as established by Euclid, to build logical arguments and proofs based on axiomatic structures.