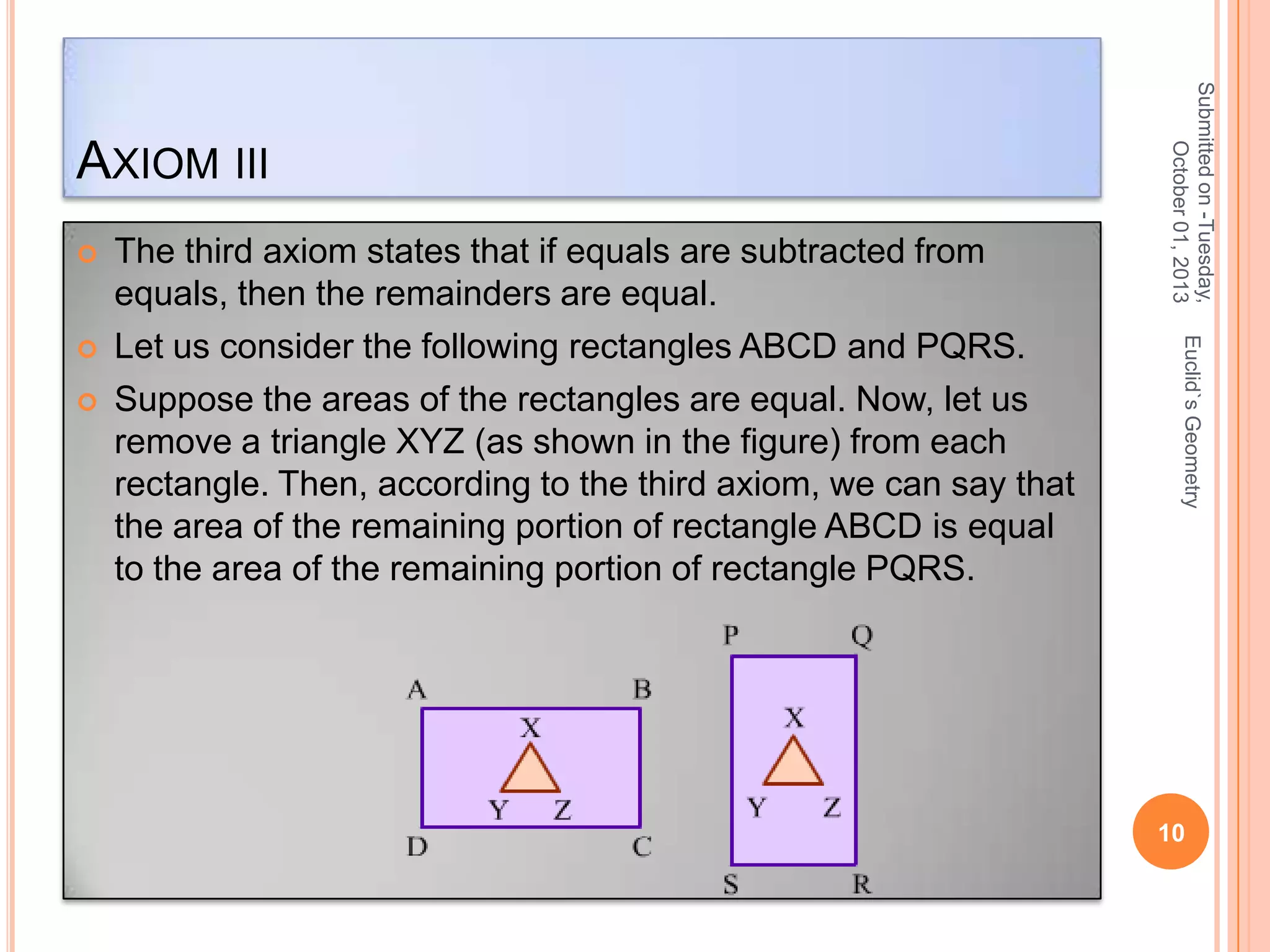
Euclid's Geometry defines basic geometric concepts like points, lines, and planes. It describes 23 definitions put forth by the ancient Greek mathematician Euclid, including the definition of a point as having no parts and of a line as having no breadth. It also explains Euclid's five postulates, such as the ability to draw straight lines between points and the property that straight lines extending infinitely will meet on the inside of two angles summing to less than two right angles. The document aims to explain Euclid's geometry clearly for students to better understand its complicated concepts.

1. INTRODUCTION TO
EUCLID`S GEOMETRY BY
1
Euclid`s Geometry
Mathematics
presentation
Submitted on -Friday, October 04, 2013

2. 
Euclid`s Geometry
Our daily life is filled with geometry—the pure
mathematics of points, lines, curves and surfaces. We
can observe various shapes and angles in the objects
that surround us. Observe, for example, this table and
its rectangular surface; the boomerang and its angular
shape; the bangle and its circular shape.
Submitted on -Tuesday,
October 01, 2013
GEOMETRY AROUND US
Euclid, an ancient Greek mathematician, observed the
various types of objects around him and tried to define
the most basic components of those objects. He
proposed twenty-three definitions based on his studies
of space and the objects visible in daily life. Let us go
through this lesson to learn each of Euclid’s definitions.
2

3. at the explanation of the very complicated Euclid geometry , so that the
students are able to see and understand it in a better way. The entire
work is done by three students of class 9,
Euclid`s Geometry
Euclidean geometry is a mathematical system attributed to the
Alexandrian Greek mathematician Euclid , which he described in his
textbook on geometry : the Elements Euclid's method consists in
assuming a small set of intuitively appealing axioms , and deducing
many other propositions (theorems ) from these. Although many of
Euclid's results had been stated by earlier mathematicians, Euclid
was the first to show how these propositions could fit into a
comprehensive deductive and logical system . The Elements begins
with plane geometry, still taught in secondary school as the first
axiomatic system and the first examples of formal proof . It goes on
to the solid geometry of three dimensions . Much of the Elements
states results of what are now called algebra and number theory
,explained in geometrical language .This entire project aims
Submitted on -Tuesday,
October 01, 2013
PREFACE
3

4. Postulate 2
 Postulate 3
 Postulate 4
 Postulate 5
 Conclusion

Euclid`s Geometry
Definitions of Euclid
 Introduction to axioms
 Axioms
Axiom i and ii

Axiom iii

Axiom iv and v

Axiom vi and vii
 Introduction to
Postulates
 Postulates Postulate 1

Submitted on -Tuesday,
October 01, 2013
CONTENTS
4

5. Euclid gave the definitions of a few very basic attributes of objects that are normally around us. These
definitions are listed below.
1. A point is that which has no part.

2. A line is a breadth-less length.

3. The extremities of a line are called points.

4. A straight line is one that lies evenly with the points on itself.

5. A surface is that which has length and breadth only.

6. The edges of a surface are lines.

Euclid`s Geometry

Submitted on -Tuesday,
October 01, 2013
DEFINITIONS OF EUCLID
7. A plane surface is one that lies evenly with the straight lines on itself.
5

6. 
9. When the lines containing the angle are straight, the angle is
called rectilinear.

10. When a straight line set up on another straight line makes the
adjacent angles equal to each other, each of the equal angles is
right and the straight line standing on the other is called a
perpendicular to that on which it stands.

11. An obtuse angle is an angle greater than the right angle.

12. An acute angle is an angle less than the right angle.

13. A boundary points out the limit or extent of something.

14. A figure is that which is contained by any boundary or
boundaries.
Euclid`s Geometry
8. A plane angle is the inclination to each other of two lines in a
plane, which meet each other and do not lie in a straight line.
Submitted on -Tuesday,
October 01, 2013

6

7. Euclid’s Axioms

Euclid assumed certain properties to be universal truths that
did not need to be proved. He classified these properties as
axioms and postulates. The properties that were not specific
to geometry were referred to as common notions or axioms.

He compiled all the known mathematical works of his time into
the Elements. Each book of the Elements contains a series of
propositions or theorems, varying in number from about ten to
hundred. These propositions or theorems are preceded by
definitions. In Book I, twenty-three definitions are followed by
five postulates. Five common notions or axioms are listed
after the postulates.

In this lesson, we will study some of Euclid’s axioms.
Euclid`s Geometry

Submitted on -Tuesday,
October 01, 2013
INTRODUCTION TO AXIOMS
7

8. Euclid`s Geometry
Things that are equal to the same thing are also
equal to one another (Transitive property of
equality).
 If equals are added to equals, then the wholes are
equal.
 If equals are subtracted from equals, then the
remainders are equal.
 Things that coincide with one another are equal to
one another (Reflexive Property).
 The whole is greater than the part.

Submitted on -Tuesday,
October 01, 2013
AXIOMS:
8

9. 



Now, the second axiom states that if equals are added to
equals, then the wholes are equal.
Let us take a line segment AD in which AB = CD.
Let us add BC to both sides of the above relation (‘equals
are added’). Then, according to the second axiom, we can
say that AB + BC = CD + BC, i.e., AC = BD.
Euclid`s Geometry

Let us start with the first axiom which states that things that
are equal to the same thing are also equal to one another.
Let us suppose the area of a rectangle is equal to the area
of a triangle and the area of that triangle is equal to the area
of a square. Then, according to the first axiom, the area of
the rectangle is equal to the area of the square. Similarly, if
a = b and b = c, then we can say that a = c.
Submitted on -Tuesday,
October 01, 2013
AXIOMS I AND II
9

10. 

Euclid`s Geometry

The third axiom states that if equals are subtracted from
equals, then the remainders are equal.
Let us consider the following rectangles ABCD and PQRS.
Suppose the areas of the rectangles are equal. Now, let us
remove a triangle XYZ (as shown in the figure) from each
rectangle. Then, according to the third axiom, we can say that
the area of the remaining portion of rectangle ABCD is equal
to the area of the remaining portion of rectangle PQRS.
Submitted on -Tuesday,
October 01, 2013
AXIOM III
10

11. The fourth axiom states that things that coincide with one another are
equal to one another.

This axiom is sometimes used in geometrical proofs.

Let us consider a point Q lying between points P and R of a line
segment PR, as is shown in the figure.

We can see that (PQ + QR) coincides with the line segment PR. So,
as per the fourth axiom, we can say that PQ + QR = PR.

Now, the fifth axiom states that the whole is greater than the part.

Let us again consider the line segment PR shown above. We can
see that PQ is a part of PR. So, as per the fifth axiom, we can say
that PR (i.e., the whole) is greater than PQ (i.e., the part).
Mathematically, we write it as PR > PQ.
Euclid`s Geometry

Submitted on -Tuesday,
October 01, 2013
AXIOM IV AND V
11

12. The sixth and seventh axioms are interrelated. The former states that things that are
double of the same things are equal to one another, while the latter states that things that
are halves of the same things are equal to one another.

Let us consider two identical circles with radii r1 and r2. Also, suppose their diameters
are d1 and d2 respectively.

As the circles are identical, their radii are equal.

∴ r1 = r2

Now, as per the sixth axiom, we can say that 2r1 = 2r2

∴ d1 = d2

Hence, we can say that if two circles have equal radii, then their diameters are also
equal.

Now, instead of taking the radii as equal, let us say that the diameters of the two circles
are equal. Then, as per the seventh axiom, we can say that the radii of the two circles are
also equal.
Euclid`s Geometry

Submitted on -Tuesday,
October 01, 2013
AXIOM VI AND VII
12

13. 
Euclid`s Geometry
Certain things are considered universal truths that
need not be proved. Consider, for example, the
following: the sun rises from the east; Sunday
comes after Saturday; March has 31 days. These
things are universally true; hence, they do not need
to be proven.
Similarly, certain geometrical properties are
regarded as universal truths. Euclid identified and
presented such properties in the Elements. The
properties specific to geometry were classified by
him as postulates. In Book I, twenty-three
definitions are followed by five postulates. Let us
learn these postulates in this lesson.
Submitted on -Tuesday,
October 01, 2013
INTRODUCTION TO POSTULATES
13

14. Euclid`s Geometry
"To draw a straight line from any point to any
point."
 "To produce [extend] a finite straight line
continuously in a straight line."
 "To describe a circle with any centre and distance
[radius]."
 "That all right angles are equal to one another."
 The parallel postulates : "That, if a straight line
falling on two straight lines make the interior
angles on the same side less than two right
angles, the two straight lines, if produced
indefinitely, meet on that side on which are the
angles less than the two right angles."

Submitted on -Tuesday,
October 01, 2013
POSTULATES
14

15. 
Postulate 1: A straight line may be drawn from any point to any other point.
Proof: Finally proved only yesterday, we must refer to the third and second postulate in order to fully prove this
one. In order to prevent accusations of lack of rigor, I will use the still incomplete third postulate only in those
cases where it may be applied.
Now any points on the line AB must also be collinear, for otherwise a straight line could not have been drawn.
Hence, it is also possible to draw a line from A to any point upon the line.
Now, let us rotate the line, such that the collinear point A is the centre of the circle so produced.
Now, it is possible to draw a straight line from A to any point in the circle. This is because the radius of the circle
is a straight line, and upon rotation, it covers all the points in the circle, implying that a straight line can be drawn
from all the points covered by the radius to the center of the circle, which is A.
Euclid`s Geometry
Take any two collinear points A and B, where collinear means it is possible to draw a straight line between them.
It is possible therefore to draw a straight line between them.
Submitted on -Tuesday,
October 01, 2013
1ST POSTULATE
Therefore all points in the circle are collinear to A i.e. they produce a straight line to A.
It is easy to show that all points in the plane are collinear: merely extend the radius infinitely, so the resultant
circle encompasses the entire region.
Repeating the above for any point in the circle, we see that it is possible to draw a straight line from that point to
any other point in its circle, and so on.
From the information above, we can deduce that all points are collinear to each other, or
It is possible to draw a straight line from any one point to any other point.
Hence proved.
15

16. 
Postulate 2: A finite straight line may be extended indefinitely.
This implies that there are an infinite number of collinear
points, as any operation with infinity that does not involve
another infinity results in infinity. By collinear, I mean points
between which a straight line may be drawn. ( I clarify this in
order to prevent accusations of using a circular argument with
the first postulate)
This implies that a line may be extended infinitely.
Euclid`s Geometry
Proof: There are an infinite number of points in a region.
Submitted on -Tuesday,
October 01, 2013
2ND POSTULATE
16

17. 
Postulate 3: A circle may be drawn with any center and any radius.
Note: By the term "collinear", I mean that it is possible to draw straight line from it
another specific point.
Taking point A as centre, we may look at the radius as a line. By Postulate 2, we
know that line may be extended indefinitely.
Therefore, the radius may be extended indefinitely.
Euclid`s Geometry
Proof: This is a little trickier to prove, so I divided the problem down into two parts.
I will first prove that a circle may have any radius.
Submitted on -Tuesday,
October 01, 2013
3RD POSTULATE
This implies that a circle may have any radius.
The second part is to prove that a circle may have any center.
Taking any collinear point, we see that it is possible to draw a straight line between
this and any other straight line.
By rotating the line by 360 degrees, we obtain a circle.
This implies that any collinear point may be the center of a circle, as the straight
line that can be drawn may be considered a radius, and rotating the radius
produces a circle.
17

18. 
Postulate 4: All right angles are equal to each other.
Proof: Let us assume that this is not true, and all right angles are not
equal to each other.
Therefore, by reduction ad absurdum, we see that all right angles must be
equal to each other.
Euclid`s Geometry
This instantly leads to a contradiction, as it implies that a triangle may
have more than one right angle.
Submitted on -Tuesday,
October 01, 2013
4TH POSTULATE
Another proof is by looking at the definition of a right angle. A right angle
is any angle equal to 90 degrees.
We know that 90 = 90 = 90 ...
We see therefore that all right angles are equal to 90 degrees and as 90
degrees is equal to 90 degrees,
this implies that all right angles are equal to each other.
Hence proved.
18

19. 
Postulate 5: If a straight line falling on two straight lines makes the interior angles
on the same side less than two right angles, the two straight lines, if produced
indefinitely, meet on that side on which the angles are less than two right angles.
From the diagram, we see that if we extend the lines indefinitely, we eventually get
a triangle.
It has been proved that the sum of the angles of a triangle sum to 180 degrees.
This implies that the two angles formed by the third line which goes through the
other two lines) cannot be equal to 180 degrees, as it would then violate the angle
sum property of that triangle.
The triangle is only possible if the two angles are not equal to 180 degrees or
more. This implies that the lines may only meet on those sides where the angles
together sum up to less than 180 degrees.
Therefore, this implies that no line which produces an obtuse or acute angle may be
parallel to l. Therefore, the only other angle possible is a right angle, which taken in
conjunction with the other interior angle forms 180 degrees, implying that any line
which produces 90 degrees with the perpendicular is always parallel to line l.
Euclid`s Geometry
Proof: This means to say that the two lines meet on the side whose sum is less
than 180 degrees.
Submitted on -Tuesday,
October 01, 2013
5TH POSTULATE
19

20. Euclid`s Geometry
We am thankful to Sir Rabin for contributing their valuable
suggestions in improving this PowerPoint presentation. We are
confident that this presentation would help to provide different
pleasures.
Submitted on -Tuesday,
October 01, 2013
CONCLUSION
20