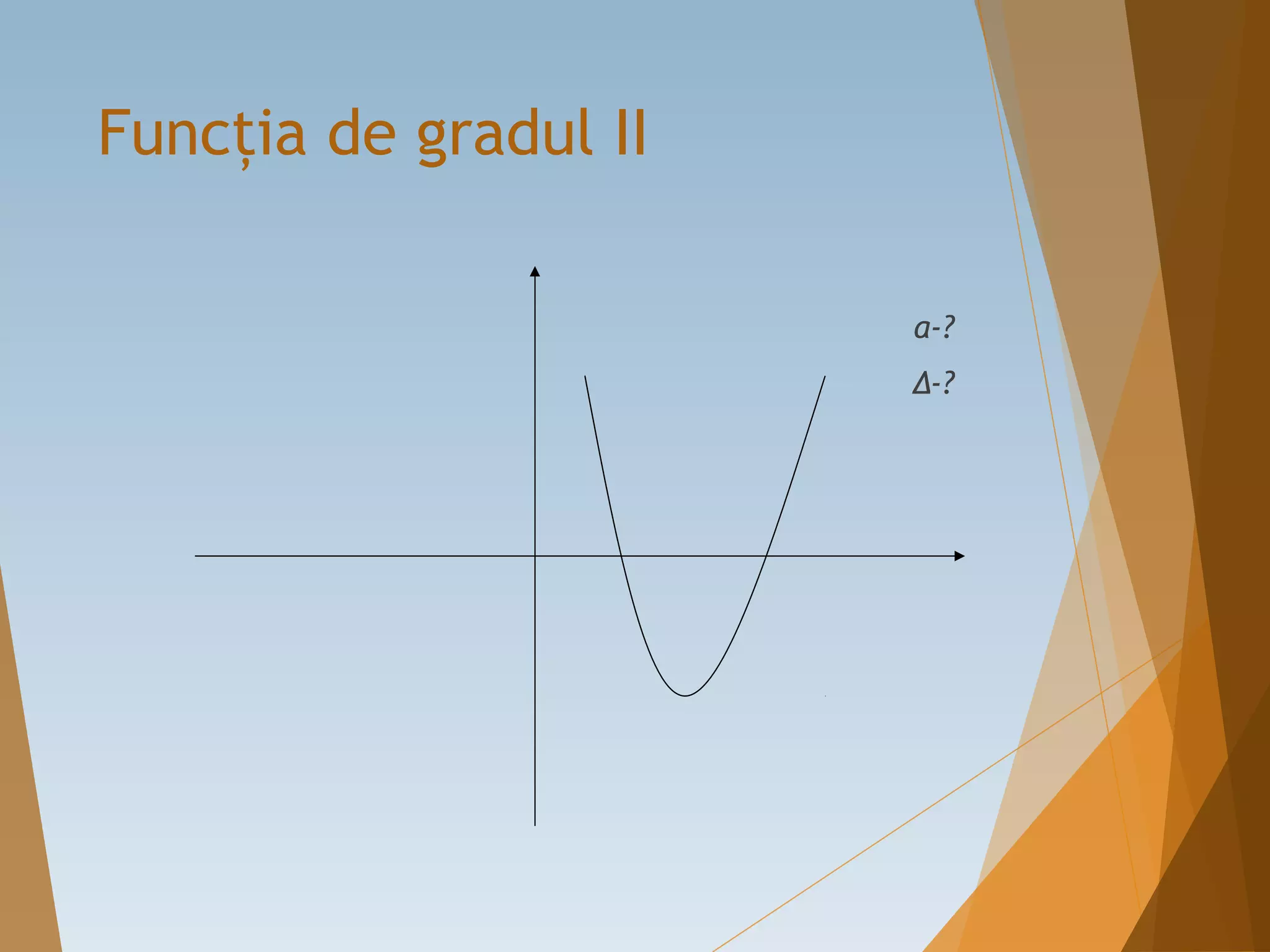
Documentul discută noțiunea de funcție, definind-o ca un triplet care asociază fiecărui element dintr-o mulțime un unic element dintr-o altă mulțime. Se explică diferite tipuri de funcții, cum ar fi funcțiile de gradul I și II, precum și proprietățile lor, precum monotonia și graficele. De asemenea, sunt prezentate exemple de funcții și moduri de a le construi grafic.