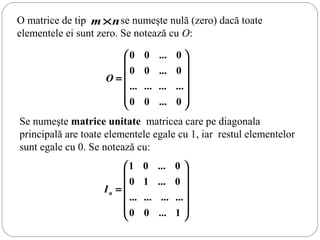
Documentul definește conceptele de matrice, inclusiv tipuri variate, cum ar fi matricele linie, coloană, pătratice, zero și unitate. De asemenea, sunt prezentate operațiile de bază cu matrici, cum ar fi egalitatea, suma și produsul, împreună cu proprietățile acestora. În final, documentul include exerciții pentru a verifica înțelegerea acestor concepte.