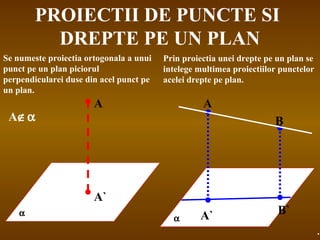
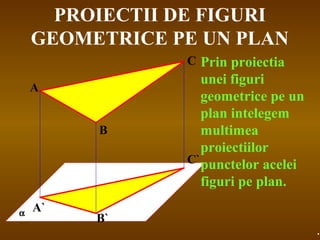
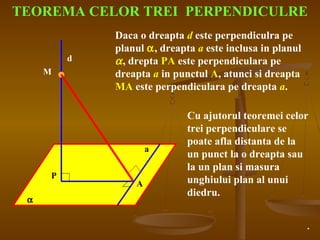
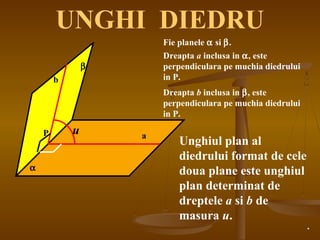
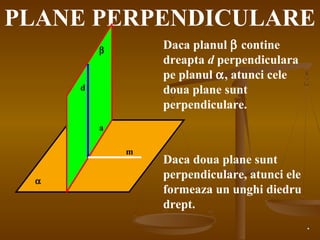
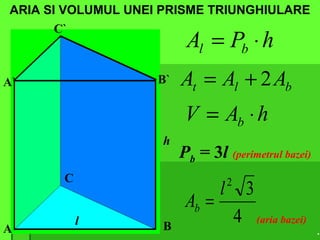
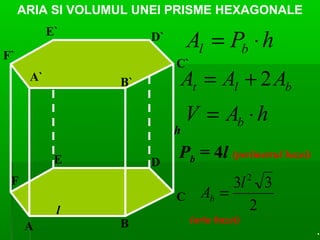
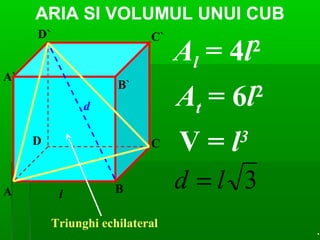
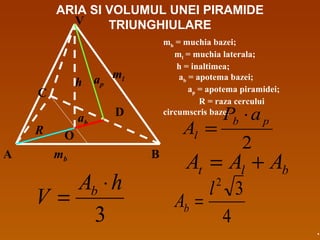
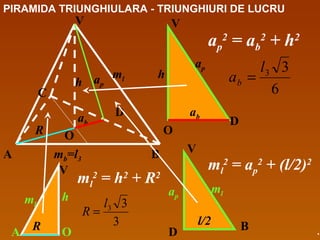
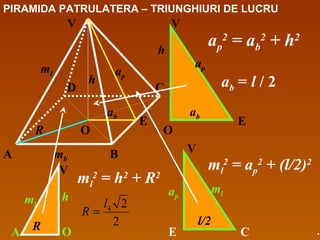
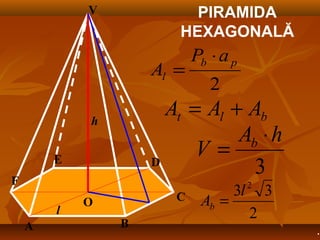
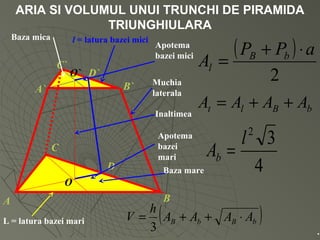
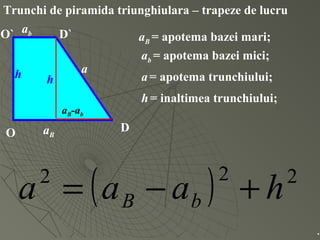
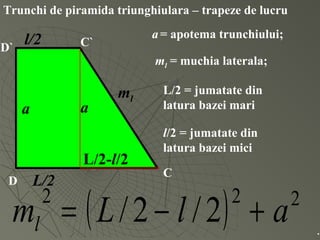
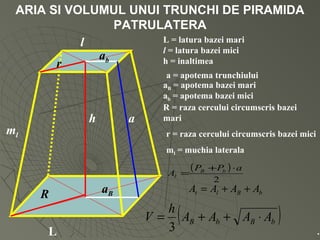
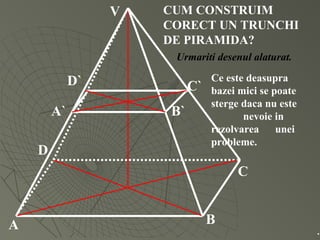
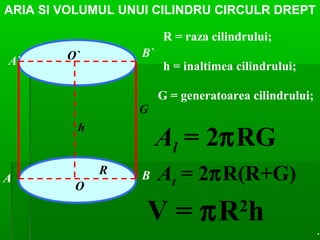
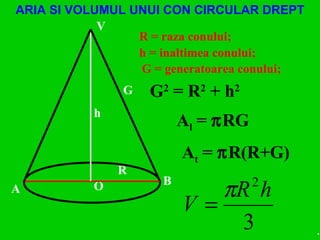
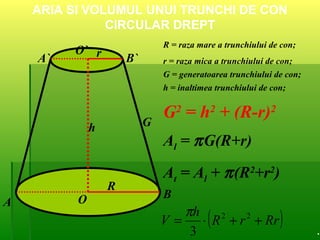
Documentul detaliază conceptele de geometrie pentru clasa a VIII-a, concentrându-se pe proiecțiile ortogonale, teorema celor trei perpendiculare și formule pentru arii și volume ale diferitelor forme geometrice, precum prisme, piramide, cilindri și conuri. De asemenea, sunt prezentate metodele de calculare a ariilor și volumelor, inclusiv pentru trunchiuri de piramide și conuri, și relația dintre corpurile similare. Are un accent pe aplicarea teoretică și practicile de construire a formelor geometrice descrise.

1. GEOMETRIECLASA a VIII-a
Semestrul I
Realizat de prof. GARCEA FLORIN
.

2. PROIECTII
ORTOGONALE
PE UN PLAN
.

3. PROIECTII DE PUNCTE SI
DREPTE PE UN PLAN
Se numeste proiectia ortogonala a unui
punct pe un plan piciorul
perpendicularei duse din acel punct pe
un plan.
α
A
A`
A∉α
Prin proiectia unei drepte pe un plan se
intelege multimea proiectiilor punctelor
acelei drepte pe plan.
α
A
B
A` B`
.

4. PROIECTII DE FIGURI
GEOMETRICE PE UN PLAN
α
A
B
C
A`
B`
C`
Prin proiectia
unei figuri
geometrice pe un
plan intelegem
multimea
proiectiilor
punctelor acelei
figuri pe plan.
.

5. UNGHIUL UNEI DREPTE CU UN PLAN
α
Ad
B
B`
d`
u
Unghiul unei drepte d cu planul α este unghiul dintre dreapta data si proiectia
acestei drepte pe plan; conform figurii de mai sus este vorba de unghiul ABB`
de masura u.
BB` = AB⋅cosu .

6. TEOREMA CELOR TREI PERPENDICULRE
d
a
α
P
M
A
Daca o dreapta d este perpendiculra pe
planul α, dreapta a este inclusa in planul
α, drepta PA este perpendiculara pe
dreapta a in punctul A, atunci si dreapta
MA este perpendiculara pe dreapta a.
Cu ajutorul teoremei celor
trei perpendiculare se
poate afla distanta de la
un punct la o dreapta sau
la un plan si masura
unghiului plan al unui
diedru.
.

7. UNGHI DIEDRU
α
P
β
a
b
u
Fie planele α si β.
Dreapta a inclusa in α, este
perpendiculara pe muchia diedrului
in P.
Dreapta b inclusa in β, este
perpendiculara pe muchia diedrului
in P.
Unghiul plan al
diedrului format de cele
doua plane este unghiul
plan determinat de
dreptele a si b de
masura u.
.

8. PLANE PERPENDICULARE
α
β
d
a
m
Daca planul β contine
dreapta d perpendiculara
pe planul α, atunci cele
doua plane sunt
perpendiculare.
Daca doua plane sunt
perpendiculare, atunci ele
formeaza un unghi diedru
drept.
.

9. ARII SI
VOLUME
.

10. ARIA SI VOLUMUL UNEI PRISME TRIUNGHIULARE
A B
C
A` B`
C`
l
h
hPA bl ⋅=
blt AAA 2+=
hAV b ⋅=
Pb = 3l (perimetrul bazei)
4
32
l
Ab =
(aria bazei)
.

11. ARIA SI VOLUMUL UNEI PRISME PATRULATERE
A B
CD
A`
B`
C`D`
hPA bl ⋅=
blt AAA 2+=
hAV b ⋅=
Pb = 4l (perimetrul bazei)
Ab = l2
(aria bazei)
l
h
.

12. ARIA SI VOLUMUL UNEI PRISME HEXAGONALE
A` B`
C`
D`E`
F`
A B
C
DE
F
l
h
hPA bl ⋅=
blt AAA 2+=
hAV b ⋅=
Pb = 4l (perimetrul bazei)
2
33 2
l
Ab =
(aria bazei)
.

13. ARIA SI VOLUMUL UNUI CUB
A B
CD
A`
B`
C`D`
l
d
Al = 4l2
At = 6l2
V = l3
3ld =
Triunghi echilateral
.

14. ARIA SI VOLUMUL UNUI PARALELIPIPED
DREPTRUNGHIC
a
b
c
d
Al = 2(a+b)c
perimetrul bazei
At = 2(ab+bc+ac)
V = abc
d2
= a2
+ b2
+ c2
(a +b +c)2
= d2
+ At
.

15. ARIA SI VOLUMUL UNEI PIRAMIDE
TRIUNGHIULARE
A B
C
V
O
D
mb
ml
h
ab
ap
R
mb = muchia bazei;
ml = muchia laterala;
h = inaltimea;
ab = apotema bazei;
ap = apotema piramidei;
R = raza cercului
circumscris bazei
2
pb
l
aP
A
⋅
=
blt AAA +=
3
hA
V b ⋅
=
4
32
l
Ab =
.

16. PIRAMIDA TRIUNGHIULARA - TRIUNGHIURI DE LUCRU
A B
C
V
O
D
mb=l3
ml
h
ab
ap
R O
D
V
ap
ab
h
ap
2
= ab
2
+ h2
6
33l
ab =
O
V
A R
ml
h
ml
2
= h2
+ R2
3
33l
R =
D B
V
mlap
l/2
ml
2
= ap
2
+ (l/2)2
.

17. ARIA SI VOLUMUL UNEI PIRAMIDE PATRULATERE
A B
E
D
V
O
C
mb
ml
h
ab
ap
R
mb = muchia bazei;
ml = muchia laterala;
h = inaltimea;
ab = apotema bazei;
ap = apotema piramidei;
R = raza cercului
circumscris bazei
2
pb
l
aP
A
⋅
=
blt AAA +=
3
hA
V b ⋅
=
Ab = l 2
.
.

18. PIRAMIDA PATRULATERA – TRIUNGHIURI DE LUCRU
A B
E
D
V
O
C
mb
ml
h
ab
ap
R
V
O
E
ap
h
ab
ap
2
= ab
2
+ h2
ab = l / 2
A
V
O
hml
R
ml
2
= h2
+ R2
2
24l
R =
E C
V
mlap
l/2
ml
2
= ap
2
+ (l/2)2
.

19. A B
C
DE
F
l
h
PIRAMIDA
HEXAGONALĂ
V
O
2
pb
l
aP
A
⋅
=
blt AAA +=
3
hA
V b ⋅
=
2
33 2
l
Ab =
.

20. ARIA SI VOLUMUL UNUI TRUNCHI DE PIRAMIDA
TRIUNGHIULARA
A B
C
A` B`
C`
O
O`
D
D`
Baza mare
Baza mica
L = latura bazei mari
l = latura bazei mici
Apotema
bazei mici
Apotema
bazei
mari
Muchia
laterala
Inaltimea
( )
2
aPP
A bB
l
⋅+
=
bBlt AAAA ++=
( )bBbB AAAA
h
V ⋅++=
3
4
32
l
Ab =
.

21. Trunchi de piramida triunghiulara – trapeze de lucru
O D
O` D`
aB
ab
h a
aB = apotema bazei mari;
ab = apotema bazei mici;
a= apotema trunchiului;
h= inaltimea trunchiului;
( ) 222
haaa bB +−=
.
h
aB-ab

22. Trunchi de piramida triunghiulara – trapeze de lucru
O
O`
A
A`
hml
R
r
h = inaltimea;
ml = muchia laterala;
R = raza cercului
circumscris bazei mari;
r = raza cercului
circumscris bazei mici;
( ) 222
hrRml +−=
.
h
R-r

23. Trunchi de piramida triunghiulara – trapeze de lucru
D
C
D` C`
a
ml
L/2
l/2
a
L/2-l/2
ml = muchia laterala;
a= apotema trunchiului;
L/2 = jumatate din
latura bazei mari
l/2 = jumatate din
latura bazei mici
( ) 222
2/2/ alLml +−= .

24. ARIA SI VOLUMUL UNUI TRUNCHI DE PIRAMIDA
PATRULATERA
L
aB
h a
l
ab
R
r
L = latura bazei mari
l = latura bazei mici
h = inaltimea
a = apotema trunchiului
aB = apotema bazei mari
ab = apotema bazei mici
R = raza cercului circumscris bazei
mari
r = raza cercului circumscris bazei miciml
ml = muchia laterala
( )
2
aPP
A bB
l
⋅+
=
bBlt AAAA ++=
( )bBbB AAAA
h
V ⋅++=
3 .

25. CUM CONSTRUIM
CORECT UN TRUNCHI
DE PIRAMIDA?
Urmariti desenul alaturat.
Ce este deasupra
bazei mici se poate
sterge daca nu este
nevoie in
rezolvarea unei
probleme.
.
A B
C
D
A` B`
C`D`
V

26. ARIA SI VOLUMUL UNUI CILINDRU CIRCULR DREPT
A
A`
B
B`
O
O`
h
G
R
R = raza cilindrului;
h = inaltimea cilindrului;
G = generatoarea cilindrului;
Al = 2πRG
At = 2πR(R+G)
V = πR2
h .

27. ARIA SI VOLUMUL UNUI CON CIRCULAR DREPT
A
BO
V
R
h
G
R = raza conului;
h = inaltimea conului;
G = generatoarea conului;
G2
= R2
+ h2
Al = πRG
At = πR(R+G)
3
2
hR
V
π
=
.

28. ARIA SI VOLUMUL UNUI TRUNCHI DE CON
CIRCULAR DREPT
A
B
A` B`
O
O`
R
G
r
h
R = raza mare a trunchiului de con;
r = raza mica a trunchiului de con;
G = generatoarea trunchiului de con;
h = inaltimea trunchiului de con;
G2
= h2
+ (R-r)2
Al = πG(R+r)
At = Al + π(R2
+r2
)
( )RrrR
h
V ++⋅= 22
3
π
.

29. RAPORTUL
ARIILOR SI
VOLUMELOR
CORPURILOR
ASEMENEA
Piramidamica
Piramidamare
2
k
A
A
maripiramidei
micipiramidei
=
3
k
V
V
maripiramidei
micipiramidei
=
Unde k este raportul de asemanare, de exemplu:
k =
h`
h`
h
h
.

30. ARIA SI VOLUMUL UNEI SFERE
O
A
R
R = raza sferei
Asferei = 4πR2
3
4 3
r
V
π
=
.

31. VREAU SA MA MAI UIT O DATA !
sfârşit