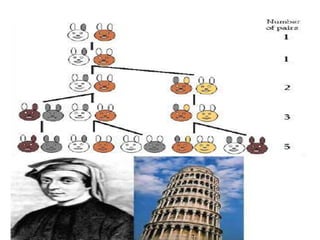
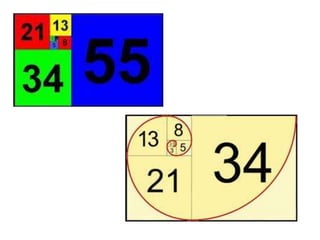
Cartea 'Şiruri' de Leonardo da Vinci examinează noțiunea de șir de numere reale, evidențiind diferențele dintre un șir și o mulțime. Aceasta oferă exemple de diverse tipuri de șiruri, modalități de definire și aplicații în științe diverse, inclusiv în biologie și muzică. De asemenea, se discută despre șirul lui Fibonacci și apariția acestuia în natură și artă.