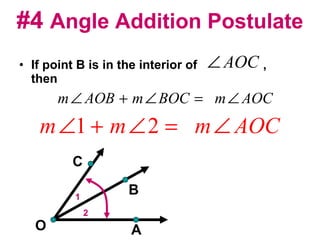
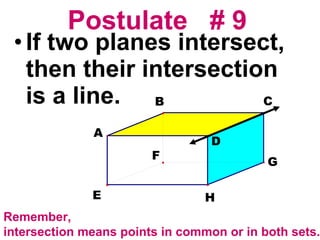
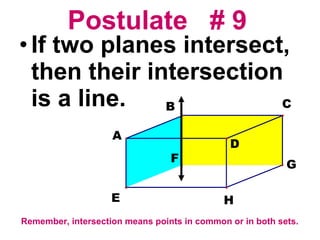
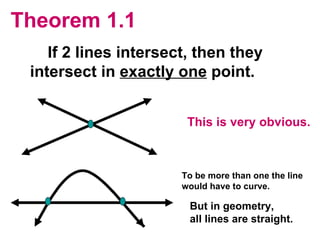
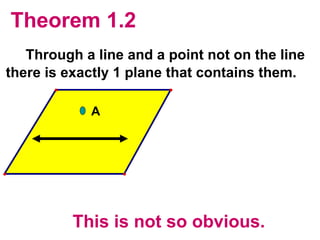
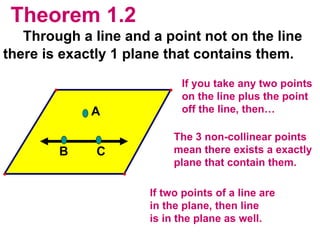
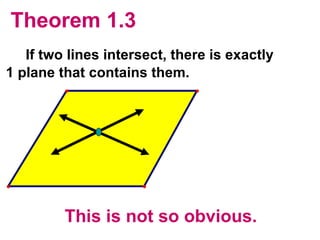
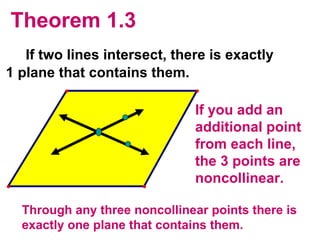
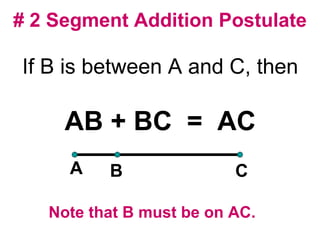
The document discusses the key postulates and theorems relating to points, lines, and planes in geometry. It defines 9 postulates that serve as basic axioms about these concepts, including the ruler postulate, segment addition postulate, and protractor postulate. It then introduces 3 theorems that can be proven based on these postulates, such as the theorem that if two lines intersect, they intersect at exactly one point. The document emphasizes that postulates are accepted as true without proof, while theorems are important statements that can be proven to be true.

1. Millau Bridge Sir Norman Foster Point, Lines, Planes, Angles Fallingwaters Frank Lloyd Wright Millenium Park Frank Lloyd Wright 1.5 Postulates and Theorems Relating to Pts, Lines and Planes

2. Postulates Are statements accepted as true without proof . They are accepted on faith alone . They are considered self-evident statements.

3. #1 Ruler Postulate A] The points on a line can be paired with the real numbers in such a way that any two points can have coordinates 0 and 1. We know this as the number line. 0 - 4 -2 6 4 2 Whole numbers and fractions are not enough to fill up the points on a line. The spaces that are missing are filled by the irrational numbers.

4. #1 Ruler Postulate B] Once a coordinate system has been chosen in this way, the distance between any two points equals the absolute value of the difference of their coordinates. This is the more important part. a b Distance =

5. # 2 Segment Addition Postulate If B is between A and C, then AB + BC = AC A B C Note that B must be on AC.

6. #3 Protractor Postulate On AB in a given plane, chose any point O between A and B. Consider OA and OB and all the rays that can be drawn from O on one side of AB. These rays can be paired with the real numbers from 0 to 180 in such a way that: OA is paired with 0. and OB is paired with 180. If OP is paired with x and OQ with y, then

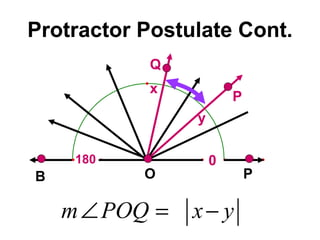
7. Relax! You don’t have to memorize this. Restated: 1] All angles are measured between 0 0 and 180 0 . 2] They can be measured with a protractor. 3] The measurement is the absolute values of the numbers read on the protractor. 4] The values of 0 and 180 on the protractor were arbitrarily selected.

8. Protractor Postulate Cont. 0 180 Q P B O P x y

9. #4 Angle Addition Postulate If point B is in the interior of , then O A B C 1 2

10. #4 Angle Addition Postulate If is a straight angle and B is any point not on AC , then O A B C These angles are called “linear pairs.” 1 2

11. Postulate #5 A line contains at least 2 points; a plane contains at least 3 non-collinear points; Space contains at least 4 non-coplanar points.

12. Postulate #5 A line is determined by 2 points. A plane is determined by 3 non-collinear points. Space is determined by 4 non-coplanar points.

13. Postulate # 6 Through any two points there is exactly one line. Restated: 2 points determine a unique line.

14. Postulate # 7 Through any three points there is at least one plane. And through any three non-collinear points there is exactly one plane.

15. Three collinear points can lie on multiple planes. While three non-collinear points can lie on exactly one plane.

16. Three collinear points can lie in multiple planes – horizontal and vertical.

17. Three collinear points can lie in multiple planes – Slanted top left to bottom right and bottom left to top right.

18. With 3 non-collinear points, there is only one plane – the plane of the triangle .

19. Postulate # 8 If two points of a line are in a plane, then the line containing those points in that plane.

20. Notice that the segment starts out as vertical with only 1 pt. in the granite plane. As the top endpoint moves to the plane… The points in between move toward the plane. When the two endpoints lie in the plane the whole segment also lies in the plane.

21. Postulate # 9 If two planes intersect, then their intersection is a line. Remember, intersection means points in common or in both sets.

22. Postulate # 9 If two planes intersect, then their intersection is a line. Remember, intersection means points in common or in both sets.

23. Final Thoughts Postulates are accepted as true on faith alone. They are not proved. Postulates need not be memorized. Those obvious simple self-evident statements are postulates. It is only important to recognize postulates and apply them occasionally.

24. Theorems Theorems are important statements that are proved true. We will introduce three theorems with an explanation of each. We are not yet ready to learn how to prove theorems.

25. Theorem 1.1 If 2 lines intersect, then they intersect in exactly one point. This is very obvious. To be more than one the line would have to curve. But in geometry, all lines are straight.

26. Theorem 1.2 Through a line and a point not on the line there is exactly 1 plane that contains them. This is not so obvious. A

27. Theorem 1.2 Through a line and a point not on the line there is exactly 1 plane that contains them. If you take any two points on the line plus the point off the line, then… The 3 non-collinear points mean there exists a exactly plane that contain them. If two points of a line are in the plane, then line is in the plane as well. A B C

28. Theorem 1.3 If two lines intersect, there is exactly 1 plane that contains them. This is not so obvious.

29. Theorem 1.3 If two lines intersect, there is exactly 1 plane that contains them. If you add an additional point from each line, the 3 points are noncollinear. Through any three noncollinear points there is exactly one plane that contains them.

30. Summary Geometry is made of 4 parts… 1 Undefined terms: Point, Line & Plane 2 Definitions 3 Postulates 4 Theorems Statements accepted without proof. Statements that can be proven true. Primitive terms that defy definition due to circular definitions. Words that can be defined by category and characteristics that are clear, concise, and reversible.

31. Postulates 1. The Ruler Postulate 2. The Segment Addition Postulate 3. The Protractor Postulate 4. The Angle Addition Postulate Euclid’s concept of “The sum of the parts equals the whole.

32. Postulates 5. The Ruler Postulate 6. The Segment Addition Postulate 7. The Protractor Postulate 8. The Angle Addition Postulate 9. The Ruler Postulate

33. C’est fini. Good day and good luck.