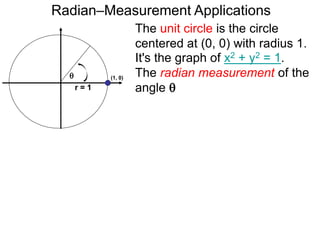
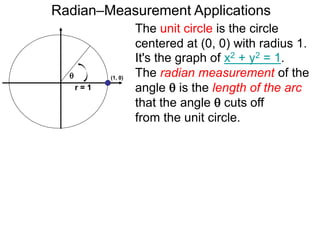
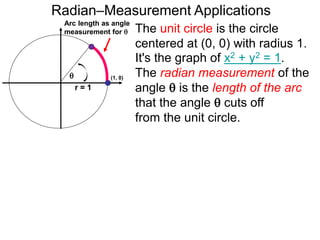
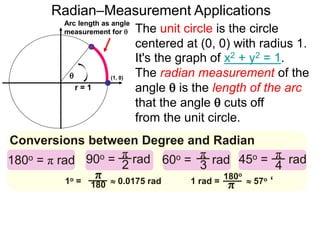
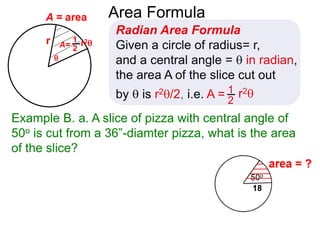
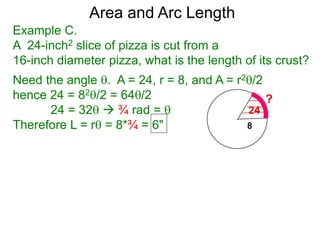
The document discusses radian measurement as it relates to angles on a unit circle. It defines the unit circle as having a radius of 1 centered at the origin, and explains that the radian measurement of an angle θ is the length of the arc cut off by θ on the unit circle. It provides conversions between radians and degrees for common angles. It then presents formulas for finding arc length and area of a sector on a circle using radian measurements of the central angle. Examples applying these formulas to find the crust length and area of a pizza slice are also included.

1. Radian–Measurement Applications

r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
(1, 0)

2. Radian–Measurement Applications

r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
(1, 0)
It's the graph of x2 + y2 = 1.

3. Radian–Measurement Applications

r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle 
(1, 0)

4. Radian–Measurement Applications

r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle  is the length of the arc
that the angle  cuts off
from the unit circle.
(1, 0)

5. Arc length as angle
measurement for 
Radian–Measurement Applications

r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle  is the length of the arc
that the angle  cuts off
from the unit circle.
(1, 0)

6. Arc length as angle
measurement for 
Radian–Measurement Applications

r = 1
Conversions between Degree and Radian
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle  is the length of the arc
that the angle  cuts off
from the unit circle.
180o = π rad
(1, 0)

7. Arc length as angle
measurement for 
Radian–Measurement Applications

r = 1
Conversions between Degree and Radian
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle  is the length of the arc
that the angle  cuts off
from the unit circle.
180o = π rad 90o = radπ
2
(1, 0)

8. Arc length as angle
measurement for 
Radian–Measurement Applications

r = 1
Conversions between Degree and Radian
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle  is the length of the arc
that the angle  cuts off
from the unit circle.
180o = π rad 90o = radπ
2 60o = radπ
3 45o = radπ
4
(1, 0)

9. Arc length as angle
measurement for 
Radian–Measurement Applications

r = 1
Conversions between Degree and Radian
π
180 π
180o
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle  is the length of the arc
that the angle  cuts off
from the unit circle.
1o =  0.0175 rad 1 rad =  57o ‘
180o = π rad 90o = radπ
2 60o = radπ
3 45o = radπ
4
(1, 0)

10. Arc length as angle
measurement for 
Radian–Measurement Applications

r = 1
Conversions between Degree and Radian
π
180 π
180o
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of x2 + y2 = 1.
The radian measurement of the
angle  is the length of the arc
that the angle  cuts off
from the unit circle.
1o =  0.0175 rad 1 rad =  57o ‘
180o = π rad 90o = radπ
2 60o = radπ
3 45o = radπ
4
(1, 0)
The advantage of using circular–lengths (radians)
to measure angles is that formulas concerning circles
may be stated with greater simplicity.

11. An angle  based at the center of
a circle is called a central angle.
r
Arc Length Formula


12. Radian Arc-Length Formula
An angle  based at the center of
a circle is called a central angle.
r
Arc Length Formula


13. Radian Arc-Length Formula
Given a circle of radius = r
and a central angle  in radian,
let L = length of the arc cuts off by
the angle ,
An angle  based at the center of
a circle is called a central angle.
r
Arc Length Formula


14. Radian Arc-Length Formula
Given a circle of radius = r
and a central angle  in radian,
let L = length of the arc cuts off by
the angle , then
L = r
An angle  based at the center of
a circle is called a central angle.
r
Arc Length Formula

L = r
L= arc length

15. Radian Arc-Length Formula
Given a circle of radius = r
and a central angle  in radian,
let L = length of the arc cuts off by
the angle , then
L = r
An angle  based at the center of
a circle is called a central angle.
r
Arc Length Formula

L = r
L= arc length
This formula is based on the following proportion
which demonstrates the advantage of using radian.

16. Radian Arc-Length Formula
Given a circle of radius = r
and a central angle  in radian,
let L = length of the arc cuts off by
the angle , then
L = r
An angle  based at the center of
a circle is called a central angle.
r
Arc Length Formula

L = r
L= arc length
This formula is based on the following proportion
which demonstrates the advantage of using radian.
arc length : circumference = L : 2πr =  : 2π (in rad)
2πr
L =
2π
or

17. Radian Arc-Length Formula
Given a circle of radius = r
and a central angle  in radian,
let L = length of the arc cuts off by
the angle , then
L = r
An angle  based at the center of
a circle is called a central angle.
r
Arc Length Formula

L = r
L= arc length
This formula is based on the following proportion
which demonstrates the advantage of using radian.
arc length : circumference = L : 2πr =  : 2π (in rad)
2πr
L =
2π
or clear denominators, we´ve
L = r

18. Arc Length Formula
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?

19. Arc Length Formula
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
50o
18
?
a.

20. Arc Length Formula
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o
18
?
a.

21. Arc Length Formula
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o = 50*(π/180 rad) = 5π/18 rad,
50o
18
?
a.

22. Arc Length Formula
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o = 50*(π/180 rad) = 5π/18 rad, with r = 18,
the length of the crust is r = 18·
5π
18 = 5π  15.7"
50o
18
?
a.

23. Arc Length Formula
b. A slice of pizza cut from a pizza with 32” diameter
has a crust measured 12”. Find its central angle.
Give the answer in radian and degree.
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o = 50*(π/180 rad) = 5π/18 rad, with r = 18,
the length of the crust is r = 18·
5π
18 = 5π  15.7"
50o
18
?
16
?
12
a. b.

24. Arc Length Formula
Given that r = 16" and L = 12",
therefore 16· = 12
b. A slice of pizza cut from a pizza with 32” diameter
has a crust measured 12”. Find its central angle.
Give the answer in radian and degree.
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o = 50*(π/180 rad) = 5π/18 rad, with r = 18,
the length of the crust is r = 18·
5π
18 = 5π  15.7"
50o
18
?
16
?
12
a. b.

25. Arc Length Formula
Given that r = 16" and L = 12",
therefore 16· = 12 or that
 = 12/16 = ¾ rad
b. A slice of pizza cut from a pizza with 32” diameter
has a crust measured 12”. Find its central angle.
Give the answer in radian and degree.
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o = 50*(π/180 rad) = 5π/18 rad, with r = 18,
the length of the crust is r = 18·
5π
18 = 5π  15.7"
50o
18
?
16
?
12
a. b.

26. Arc Length Formula
Given that r = 16" and L = 12",
therefore 16· = 12 or that
 = 12/16 = ¾ rad
b. A slice of pizza cut from a pizza with 32” diameter
has a crust measured 12”. Find its central angle.
Give the answer in radian and degree.
180o
πin degree,  = ¾ rad = ¾ *
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o = 50*(π/180 rad) = 5π/18 rad, with r = 18,
the length of the crust is r = 18·
5π
18 = 5π  15.7"
50o
18
?
16
?
12
a. b.

27. Arc Length Formula
Given that r = 16" and L = 12",
therefore 16· = 12 or that
 = 12/16 = ¾ rad
b. A slice of pizza cut from a pizza with 32” diameter
has a crust measured 12”. Find its central angle.
Give the answer in radian and degree.
180o
π
135o
πin degree,  = ¾ rad = ¾ * = ≈ 43.0o
Example A.
a. A slice of pizza with central angle of 50o is cut from
a 36”-diamter pizza, what is the length of its crust?
The point here is that we need radian!
50o = 50*(π/180 rad) = 5π/18 rad, with r = 18,
the length of the crust is r = 18·
5π
18 = 5π  15.7"
50o
18
?
16
?
12
a. b.

28. r

Area Formula
Radian Area Formula

29. r

Area Formula
Radian Area Formula
Given a circle of radius= r,
and a central angle =  in radian,
the area A of the slice cut out
by  is r2/2, i.e. A = r21
2

30. r

A = area Area Formula
Radian Area Formula
Given a circle of radius= r,
and a central angle =  in radian,
the area A of the slice cut out
by  is r2/2, i.e. A = r21
2
A= r21
2

31. r

A = area Area Formula
Radian Area Formula
Given a circle of radius= r,
and a central angle =  in radian,
the area A of the slice cut out
by  is r2/2, i.e. A = r21
2
A= r21
2
Example B. a. A slice of pizza with central angle of
50o is cut from a 36”-diamter pizza, what is the area
of the slice?

32. r

A = area Area Formula
Radian Area Formula
Given a circle of radius= r,
and a central angle =  in radian,
the area A of the slice cut out
by  is r2/2, i.e. A = r21
2
A= r21
2
Example B. a. A slice of pizza with central angle of
50o is cut from a 36”-diamter pizza, what is the area
of the slice?

33. r

A = area
Converting degree to radian
50o = 5π/18 rad,
Area Formula
Radian Area Formula
Given a circle of radius= r,
and a central angle =  in radian,
the area A of the slice cut out
by  is r2/2, i.e. A = r21
2
A= r21
2
Example B. a. A slice of pizza with central angle of
50o is cut from a 36”-diamter pizza, what is the area
of the slice?

34. r

A = area
Converting degree to radian
50o = 5π/18 rad, with r = 18,
the area of the slice is
5π
18
Area Formula
Radian Area Formula
Given a circle of radius= r,
and a central angle =  in radian,
the area A of the slice cut out
by  is r2/2, i.e. A = r21
2
1
2
A= r21
2
r2= *182*
1
2
Example B. a. A slice of pizza with central angle of
50o is cut from a 36”-diamter pizza, what is the area
of the slice?

35. r

A = area
Converting degree to radian
50o = 5π/18 rad, with r = 18,
the area of the slice is
5π
18
Area Formula
Radian Area Formula
Given a circle of radius= r,
and a central angle =  in radian,
the area A of the slice cut out
by  is r2/2, i.e. A = r21
2
1
2
A= r21
2
r2= *182*
1
2
Example B. a. A slice of pizza with central angle of
50o is cut from a 36”-diamter pizza, what is the area
of the slice?
= 45π  141 in2

36. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?

37. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?

38. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle .

39. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle . A = 24, r = 8, and A = r2/2
hence 24 = 82/2 = 64/2

40. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle . A = 24, r = 8, and A = r2/2
hence 24 = 82/2 = 64/2
24 = 32  ¾ rad = 

41. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle . A = 24, r = 8, and A = r2/2
hence 24 = 82/2 = 64/2
24 = 32  ¾ rad = 
Therefore L = r = 8*¾ = 6"

42. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle . A = 24, r = 8, and A = r2/2
hence 24 = 82/2 = 64/2
24 = 32  ¾ rad = 
Therefore L = r = 8*¾ = 6"
Example D.
A slice of pizza with 12-inch crust is cut from a
16-inch diameter pizza, what is its area?

43. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle . A = 24, r = 8, and A = r2/2
hence 24 = 82/2 = 64/2
24 = 32  ¾ rad = 
Therefore L = r = 8*¾ = 6"
Example D.
A slice of pizza with 12-inch crust is cut from a
16-inch diameter pizza, what is its area?
The arc length L = 12, r = 8, and L = r,
hence12 = 8

44. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle . A = 24, r = 8, and A = r2/2
hence 24 = 82/2 = 64/2
24 = 32  ¾ rad = 
Therefore L = r = 8*¾ = 6"
Example D.
A slice of pizza with 12-inch crust is cut from a
16-inch diameter pizza, what is its area?
The arc length L = 12, r = 8, and L = r,
hence12 = 8 or 3/2 rad = 

45. Area and Arc Length
Example C.
A 24-inch2 slice of pizza is cut from a
16-inch diameter pizza, what is the length of its crust?
Need the angle . A = 24, r = 8, and A = r2/2
hence 24 = 82/2 = 64/2
24 = 32  ¾ rad = 
Therefore L = r = 8*¾ = 6"
Example D.
A slice of pizza with 12-inch crust is cut from a
16-inch diameter pizza, what is its area?
The arc length L = 12, r = 8, and L = r,
hence12 = 8 or 3/2 rad = 
So A = r2/2 = 82* * = 48 in21
2
3
2

46. The simplicity of these formulas is carried over to other
formulas concerning rotations.
Angular Velocity

47. The simplicity of these formulas is carried over to other
formulas concerning rotations. For example,
the angular velocity w of a rotating wheel is the
amount of angle rotated in one unit of time.
Angular Velocity

48. The simplicity of these formulas is carried over to other
formulas concerning rotations. For example,
the angular velocity w of a rotating wheel is the
amount of angle rotated in one unit of time.
The angular velocity w = (π/2) rad/sec means
the wheel rotates ¼ of a round (circle) every second.
Angular Velocity

49. The simplicity of these formulas is carried over to other
formulas concerning rotations. For example,
the angular velocity w of a rotating wheel is the
amount of angle rotated in one unit of time.
The angular velocity w = (π/2) rad/sec means
the wheel rotates ¼ of a round (circle) every second.
The angular velocity
w = (π/2) / sec
Assuming t is in second and w is in radian,
then the blue dot travels the arc length of
w*r every second.
Angular Velocity
r

50. The simplicity of these formulas is carried over to other
formulas concerning rotations. For example,
the angular velocity w of a rotating wheel is the
amount of angle rotated in one unit of time.
The angular velocity w = (π/2) rad/sec means
the wheel rotates ¼ of a round (circle) every second.
The angular velocity
w = (π/2) / sec
Assuming t is in second and w is in radian,
then the blue dot travels the arc length of
w*r every second. So in t seconds,
the linear distance D or the distance the
wheel traveled on the ground is
D = w*r*t
Angular Velocity
D=w*r*t
r

51. The simplicity of these formulas is carried over to other
formulas concerning rotations. For example,
the angular velocity w of a rotating wheel is the
amount of angle rotated in one unit of time.
The angular velocity w = (π/2) rad/sec means
the wheel rotates ¼ of a round (circle) every second.
The angular velocity
w = (π/2) / sec
Assuming t is in second and w is in radian,
then the blue dot travels the arc length of
w*r every second. So in t seconds,
the linear distance D or the distance the
wheel traveled on the ground is
D = w*r*t
and the dial have swiped over an area of
A = ½ w*r2*t.
Angular Velocity
D=w*r*t
A =½ w*r2 *t
r

52. Example D. A sphere with radius r = 5 meters is
spinning with the angular velocity w = 4π rad/sec.
a. What is its linear speed? How much distance does
a point travel along the equator in one minute?
Angular Velocity
5
w = 4π
rad/sec

53. Example D. A sphere with radius r = 5 meters is
spinning with the angular velocity w = 4π rad/sec.
a. What is its linear speed? How much distance does
a point travel along the equator in one minute?
Angular Velocity
5
w = 4π
rad/sec
Its linear speed is 4π(5) = 20π m/sec

54. Example D. A sphere with radius r = 5 meters is
spinning with the angular velocity w = 4π rad/sec.
a. What is its linear speed? How much distance does
a point travel along the equator in one minute?
Angular Velocity
5
w = 4π
rad/sec
Its linear speed is 4π(5) = 20π m/sec
There are 60 seconds in one minutes so the distance
it traveled is D = w*r*t = 4π(5)(60) = 1200π m.

55. Example D. A sphere with radius r = 5 meters is
spinning with the angular velocity w = 4π rad/sec.
a. What is its linear speed? How much distance does
a point travel along the equator in one minute?
b. How much distance does the point p on
the sphere as shown travel in one minute?
What is its linear speed?
60o
p
Angular Velocity
Its linear speed is 4π(5) = 20π m/sec
There are 60 seconds in one minutes so the distance
it traveled is D = w*r*t = 4π(5)(60) = 1200π m.
5
w = 4π
rad/sec

56. Example D. A sphere with radius r = 5 meters is
spinning with the angular velocity w = 4π rad/sec.
a. What is its linear speed? How much distance does
a point travel along the equator in one minute?
b. How much distance does the point p on
the sphere as shown travel in one minute?
What is its linear speed?
60o
p
Angular Velocity
Its linear speed is 4π(5) = 20π m/sec
There are 60 seconds in one minutes so the distance
it traveled is D = w*r*t = 4π(5)(60) = 1200π m.
5
r
The radius of the rotation is
r = 5 sin(30o) = 5/2 meters.
w = 4π
rad/sec

57. Example D. A sphere with radius r = 5 meters is
spinning with the angular velocity w = 4π rad/sec.
a. What is its linear speed? How much distance does
a point travel along the equator in one minute?
b. How much distance does the point p on
the sphere as shown travel in one minute?
What is its linear speed?
60o
p
Angular Velocity
Its linear speed is 4π(5) = 20π m/sec
There are 60 seconds in one minutes so the distance
it traveled is D = w*r*t = 4π(5)(60) = 1200π m.
5
r
The radius of the rotation is
r = 5 sin(30o) = 5/2 meters.
So p travels 600π at a linear speed of
10π m/sec.
w = 4π
rad/sec

58. Exercise
Radian–Measurement Applications
At Pizza Grande, a medium pizza has 12–inch
diameter and a large pizza has 18–inch diameter.
A large pizza is cut into 8 slices sold at $3/slice and a
medium one is cut into 6 slices and sold at $2/slice.
1. Find the perimeter and the area of a medium slice.
2. Find the perimeter and the area of a large slice.
3. Which is a better deal, a medium or a large slice?
4. We want to cut one slice from the medium pizza
that is the size of two large slices. What is the central
angle of the medium–slice?
5. We want to cut one slice from the large pizza that
is the size as three medium slices. What is the
central angle of the large–slice?

59. 6. A 25 in2 slice of pizza has a 8" crust.
How much is the rest of the pizza
7. A 25 in2 slice of pizza has a 35o central angle.
How much is the rest of the pizza
8. A slice of pizza has a 8" crust and a 35o
central angle. How much is the rest of the pizza
9. A slice of pizza cut from a pizza with 9" radius
has a 8" crust. What is the central angle of the slice?
How much is the rest of the pizza
Radian–Measurement Applications
10. A car has 18”–radius wheels is traveling with the
angular velocity of w = 10π rad/sec. How fast is car
traveling in mph?

60. Radian–Measurement Applications
11. A car has 15”–radius wheels, what is the approx.
angular velocity (rad/sec) of the wheels when it’s
traveling at a speed of 60 mph?
12. A radar spins at rate of w = π/4 rad/sec and has a
20–mile radius effective detection area.
In 3 second, how much area is scanned by the radar?
13. From problem 12, how long would it take for the
radar to scanned an area of 100 mi2?
≈ 8000 mi
Tropic
of Cancer
Arctic
Circle
≈ 23o ≈ 66o
14. Following are approximate
measurements of earth.
Find the linear speeds in mph
at the equator, at the Tropic of
Cancer and at the Arctic Circle.

61. Answers
Radian–Measurement Applications
1. p = 2π, A = 6π
3. a large slice is a better deal
5. 4π/9 rad
7. 232 in2
9. 218 in2
11. w ≈ 70.4 rad/sec
13. t = 2/π sec

62. Radian–Measurement Applications
11. A car has 15”–radius wheels, what is the approx.
angular velocity (rad/sec) of the wheels when it’s
traveling at a speed of 60 mph?
12. A radar spins at rate of w = π/4 rad/sec and has a
200–mile radius effective detection area.
In 3 second, how much area is scanned by the radar?
13. From problem 11, how long would it take for the
radar to scanned an area of 100 mi2?
≈ 8000 mi
Tropic
of Cancer
Arctic
Circle
≈ 23o ≈ 66o
14. Following are approximate
measurements of earth.
Find the linear speeds in mph
at the equator, at the Tropic of
Cancer and at the Arctic Circle.