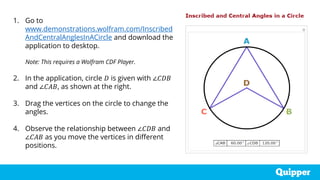
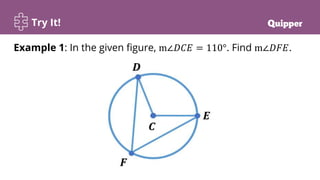
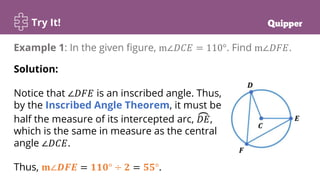
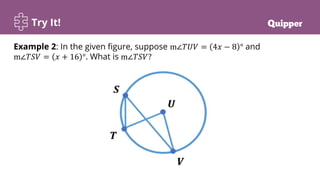
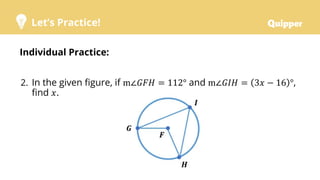
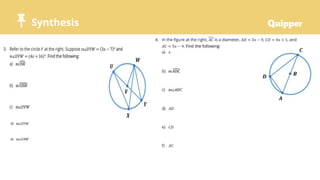
The document discusses properties of central and inscribed angles, defining the inscribed angle and semicircle theorems, showing how to find angle measures using these properties, and providing examples to solve word problems involving central and inscribed angles. Learners are guided through interactive demonstrations and individual/group practice problems to reinforce understanding and application of the key concepts.

1. Lesson 3
Properties of Central
and Inscribed Angles

2. Objectives
At the end of this lesson, the learner should be able to
● correctly define the Inscribed Angle and Semicircle
Theorems;
● correctly state the proof of Inscribed Angle and Semicircle
Theorems;
● correctly find angle and arc measures using the properties
of central and inscribed angles; and
● correctly solve word problems involving central and
inscribed angles.

3. Essential Questions
● How are inscribed angles related to central angles?
● How can you apply the properties of central and inscribed
angles in solving problems on circles?

4. Warm Up!
In the following activity, the relationship between central and
inscribed angles will be explored using an online interactive
demonstration tool for circles and angles.

5. 1. Go to
www.demonstrations.wolfram.com/Inscribed
AndCentralAnglesInACircle and download the
application to desktop.
Note: This requires a Wolfram CDF Player.
2. In the application, circle 𝐷 is given with ∠𝐶𝐷𝐵
and ∠𝐶𝐴𝐵, as shown at the right.
3. Drag the vertices on the circle to change the
angles.
4. Observe the relationship between ∠𝐶𝐷𝐵 and
∠𝐶𝐴𝐵 as you move the vertices in different
positions.

6. Guide Questions
● What kind of angle is ∠𝐶𝐷𝐵? How about ∠𝐶𝐴𝐵?
● Describe any pattern that you notice between the
measures of ∠𝐶𝐷𝐵 and ∠𝐶𝐴𝐵.
● Make a conjecture about how the measure of an inscribed
angle is related to the measure of the corresponding
central angle.

7. Learn about It!
Inscribed Angle Theorem
states that the measure of an inscribed angle is always half the measure of its
intercepted arc or the central angle
1
Example:
In circle 𝑂, if 𝐦∠𝑨𝑶𝑪 = 𝟖𝟎°, then by the
Inscribed Angle Theorem, 𝐦∠𝑨𝑩𝑪 = 𝟒𝟎°.

8. Learn about It!
Semicircle Theorem
states that if an inscribed angle intercepts a semicircle, then it is a right angle
2
Example:
In circle 𝑂, since ∠𝐴𝐵𝐶 intercepts 𝑨𝑪 = 𝟏𝟖𝟎°,
then by the Semicircle Theorem, 𝐦∠𝑨𝑩𝑪 = 𝟗𝟎°.

9. Try It!
Example 1: In the given figure, m∠𝐷𝐶𝐸 = 110°. Find m∠𝐷𝐹𝐸.

10. Try It!
Example 1: In the given figure, m∠𝐷𝐶𝐸 = 110°. Find m∠𝐷𝐹𝐸.
Solution:
Notice that ∠𝐷𝐹𝐸 is an inscribed angle. Thus,
by the Inscribed Angle Theorem, it must be
half the measure of its intercepted arc, 𝐷𝐸,
which is the same in measure as the central
angle ∠𝐷𝐶𝐸.
Thus, 𝐦∠𝑫𝑭𝑬 = 𝟏𝟏𝟎° ÷ 𝟐 = 𝟓𝟓°.

11. Try It!
Example 2: In the given figure, suppose m∠𝑇𝑈𝑉 = 4𝑥 − 8 ° and
m∠𝑇𝑆𝑉 = 𝑥 + 16 °. What is m∠𝑇𝑆𝑉?

12. Try It!
Example 2: In the given figure, suppose m∠𝑇𝑈𝑉 = 4𝑥 − 8 ° and
m∠𝑇𝑆𝑉 = 𝑥 + 16 °. What is m∠𝑇𝑆𝑉?
Solution:
1. Set up an equation relating the two angles.
Since ∠𝑇𝑈𝑉 is a central angle, and ∠𝑇𝑆𝑉 is
an inscribed angle that intercepts the same
arc, 𝑇𝑉, we have the following equation
using the Inscribed Angle Theorem:
𝟒𝒙 − 𝟖
𝟐
= 𝒙 + 𝟏𝟔

13. Try It!
Example 2: In the given figure, suppose m∠𝑇𝑈𝑉 = 4𝑥 − 8 ° and
m∠𝑇𝑆𝑉 = 𝑥 + 16 °. What is m∠𝑇𝑆𝑉?
Solution:
2. Solve for 𝒙.
4𝑥 − 8
2
= 𝑥 + 16
2
4𝑥 − 8
2
= 𝑥 + 16 2
4𝑥 − 8 = 2𝑥 + 32
4𝑥 − 2𝑥 = 32 + 8

14. Try It!
Example 2: In the given figure, suppose m∠𝑇𝑈𝑉 = 4𝑥 − 8 ° and
m∠𝑇𝑆𝑉 = 𝑥 + 16 °. What is m∠𝑇𝑆𝑉?
Solution:
2. Solve for 𝒙.
4𝑥 − 2𝑥 = 32 + 8
2𝑥 = 40
𝒙 = 𝟐𝟎

15. Try It!
Example 2: In the given figure, suppose m∠𝑇𝑈𝑉 = 4𝑥 − 8 ° and
m∠𝑇𝑆𝑉 = 𝑥 + 16 °. What is m∠𝑇𝑆𝑉?
Solution:
3. Determine m∠𝑇𝑆𝑉.
Substituting 𝒙 = 𝟐𝟎 into the expression for m∠𝑇𝑆𝑉, we
have
m∠𝑇𝑆𝑉 = 𝑥 + 16 °
m∠𝑇𝑆𝑉 = 𝟐𝟎 + 16 °
m∠𝑇𝑆𝑉 = 𝟑𝟔°

16. Try It!
Example 2: In the given figure, suppose m∠𝑇𝑈𝑉 = 4𝑥 − 8 ° and
m∠𝑇𝑆𝑉 = 𝑥 + 16 °. What is m∠𝑇𝑆𝑉?
Solution:
3. Determine m∠𝑇𝑆𝑉.
Therefore, 𝐦∠𝑻𝑺𝑽 = 𝟑𝟔°.

17. Let’s Practice!
Individual Practice:
1. In the given figure, m∠𝐼𝐿𝐽 = 25°. What is m∠𝐼𝐾𝐽?

18. Let’s Practice!
Individual Practice:
2. In the given figure, if m∠𝐺𝐹𝐻 = 112° and m∠𝐺𝐼𝐻 = 3𝑥 − 16 °,
find 𝑥.

19. Let’s Practice!
Group Practice: Form 6 groups of students.
Three flowering shrubs are arranged
in a circular garden, as shown in the
figure. The distance between the
blue and yellow shrub is equal to 20
feet, and the distance between the
blue and red shrub is 15 feet. If the
yellow and red shrubs lie on the
diameter of the garden, what is the
distance between them?

20. Key Points
Inscribed Angle Theorem
states that the measure of an inscribed angle is always half the measure of its
intercepted arc or the central angle
1
Semicircle Theorem
states that if an inscribed angle intercepts a semicircle, then it is a right angle
2

21. Synthesis
● What is the Inscribed Angle Theorem? How about the
Semicircle Theorem?
● What challenges did you encounter while solving problems
involving central and inscribed angles? How did you deal with
them?
● Can you use the Central Angle Postulate or the Inscribed Angle
Theorem in finding the angle measures formed by intersecting
chords?

22. Synthesis
Activity 1

23. Synthesis

24. Synthesis
Activity 2