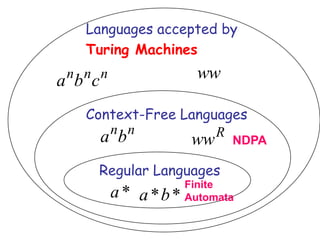
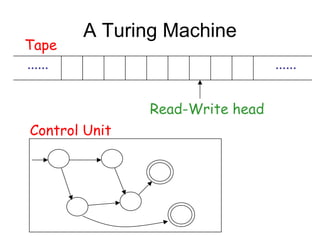
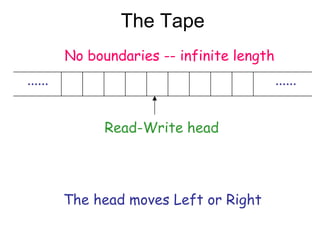
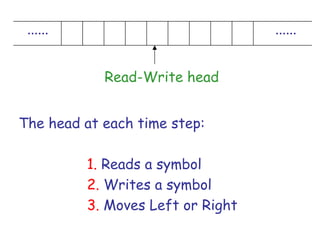
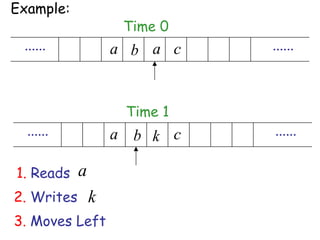
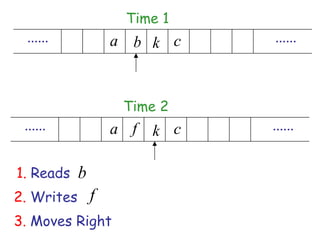
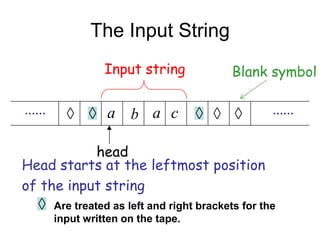
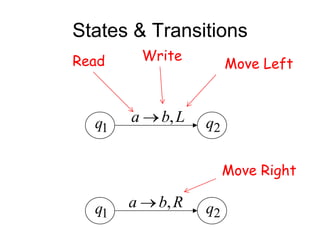
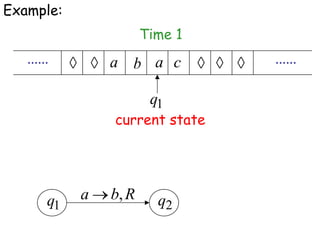
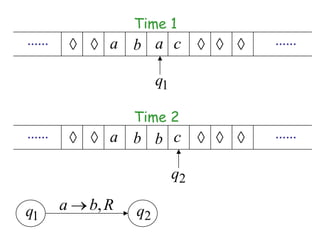
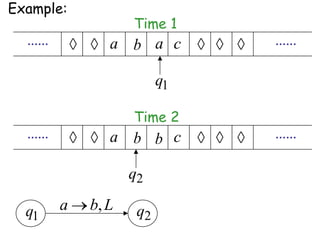
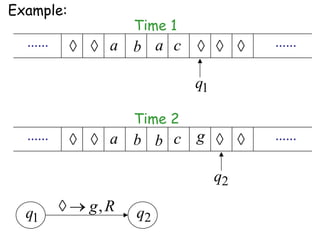
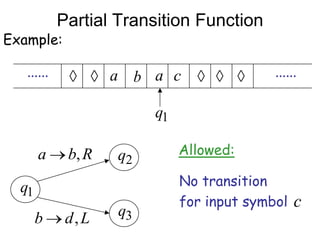
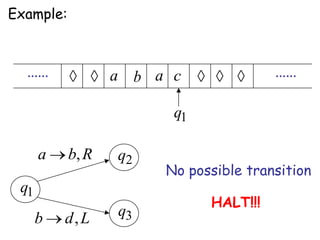
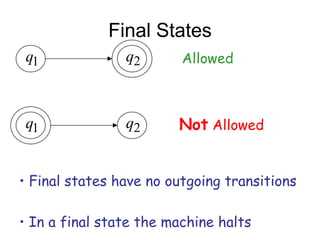
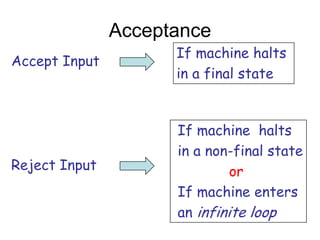
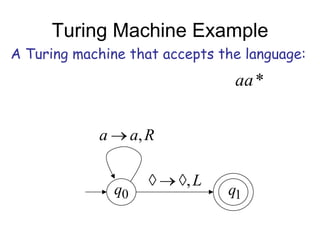
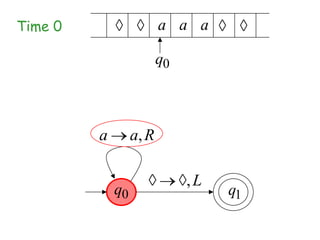
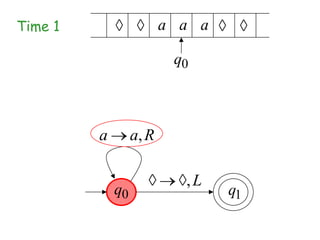
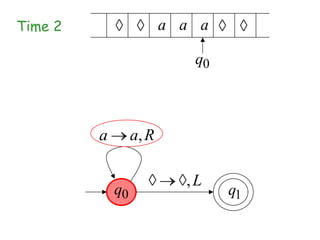
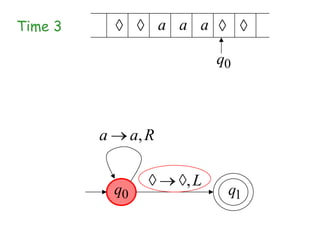
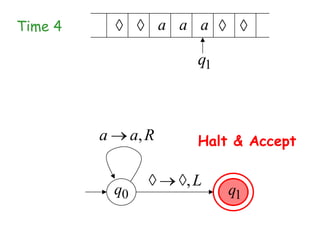
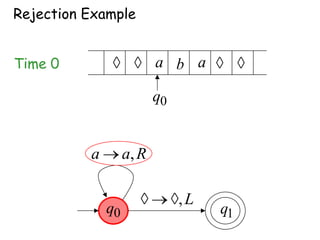
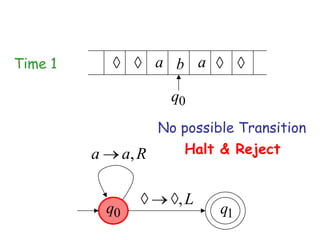
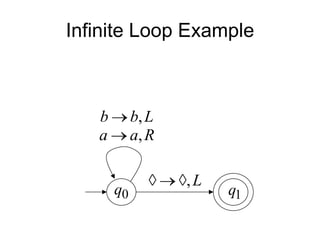
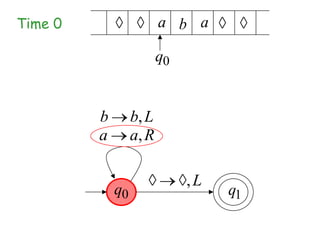
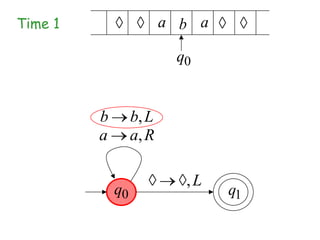
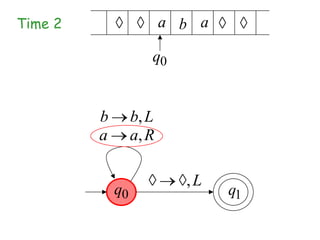
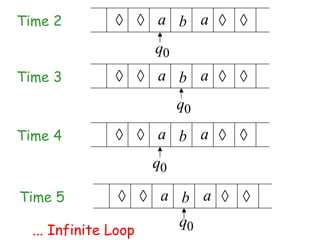
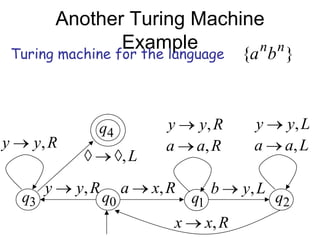
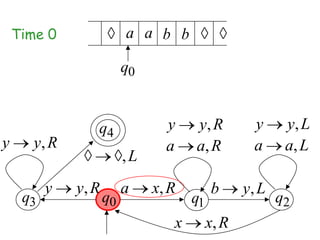
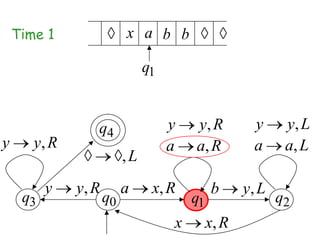
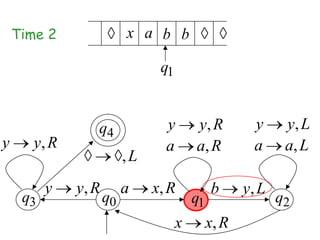
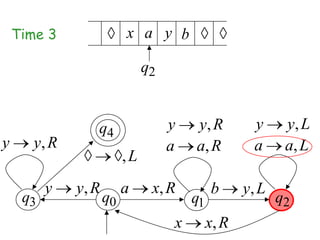
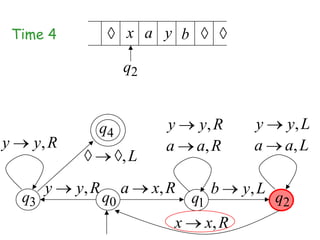
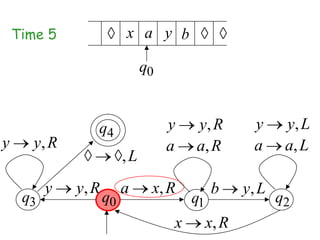
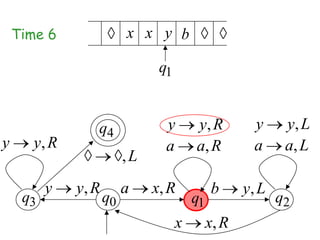
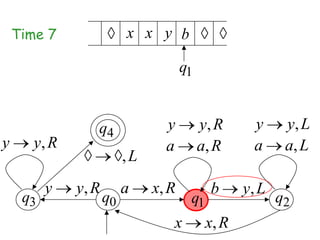
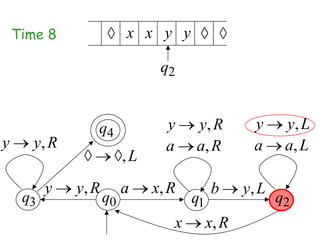
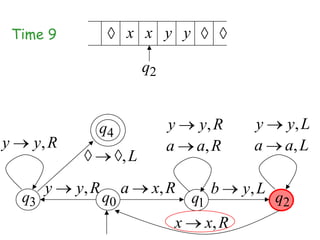
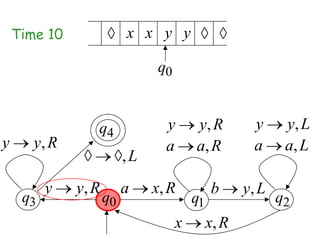
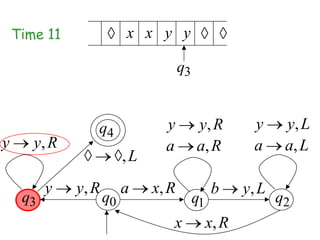
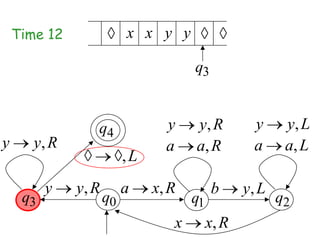
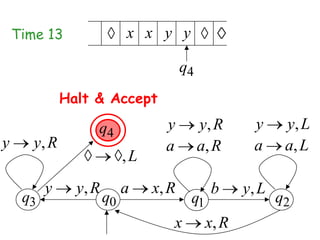
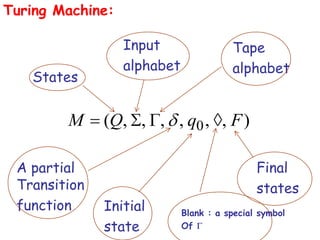
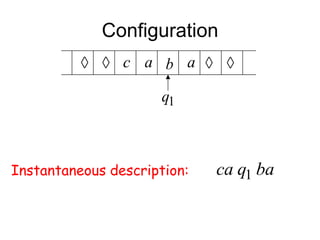
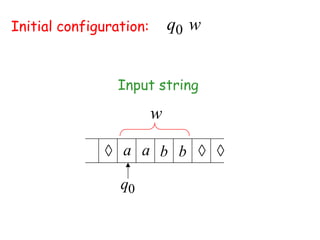
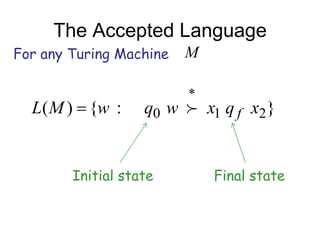
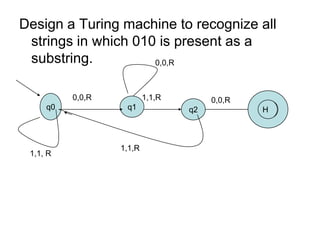
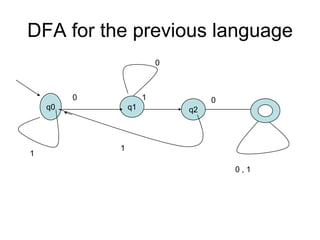
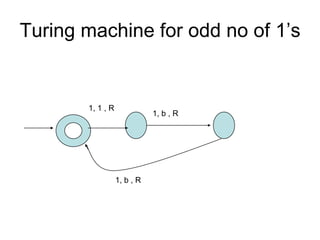
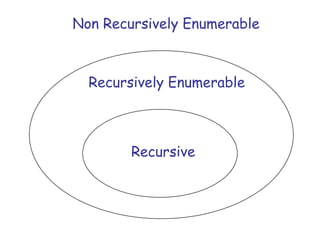
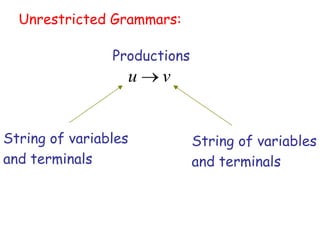
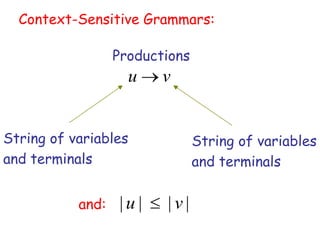
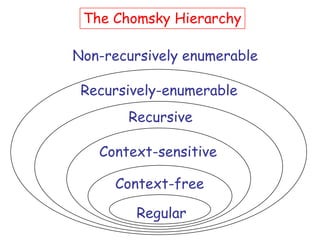
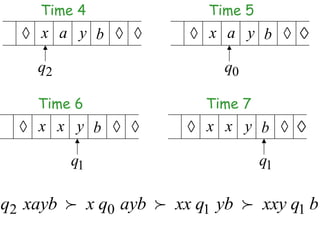Turing Machines are a simple mathematical model of a general purpose computer invented by Alan Turing in 1936. A Turing Machine consists of an infinite tape divided into cells, a head that reads and writes symbols on the tape, a finite set of states, and transition rules determining the behavior of the machine. The machine operates by reading a symbol on the tape, updating the symbol according to its transition rules, moving the head left or right, and transitioning to a new state. Turing Machines can simulate any algorithm and are capable of performing any calculation that can be performed by any computing machine.