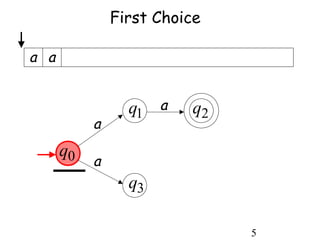
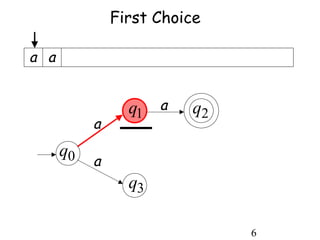
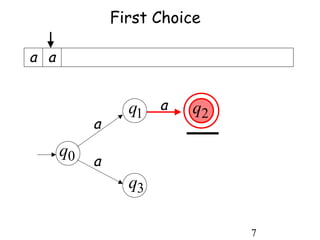
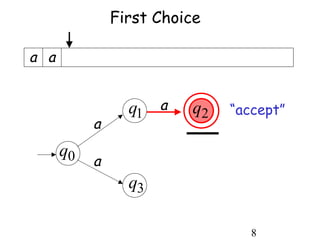
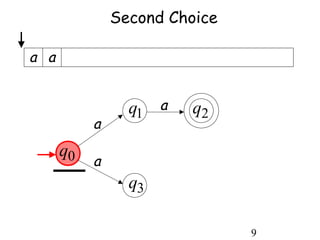
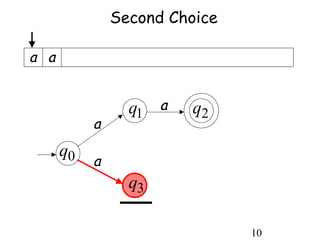
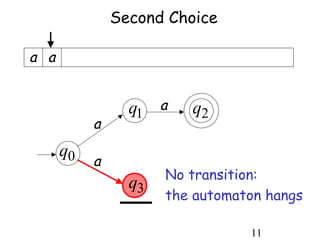
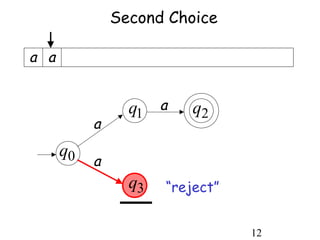
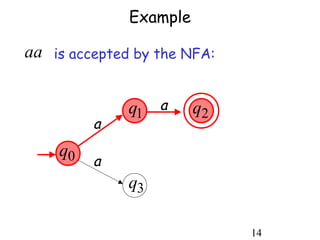
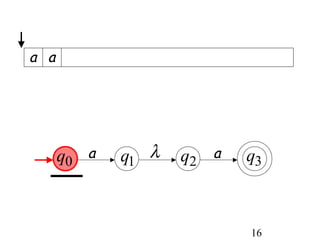
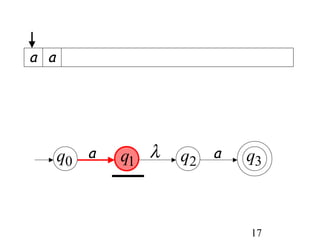
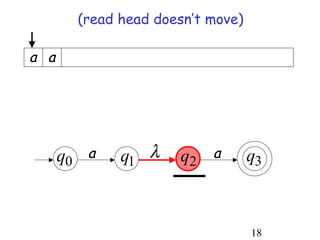
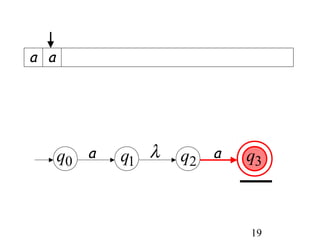
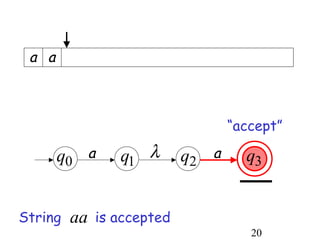
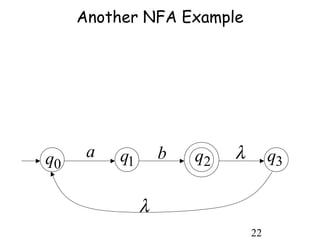
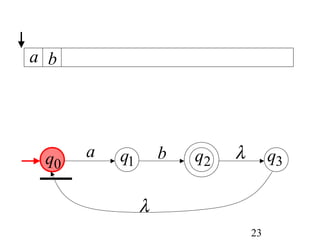
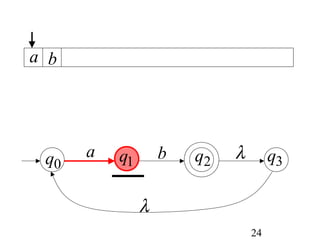
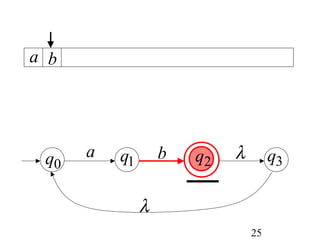
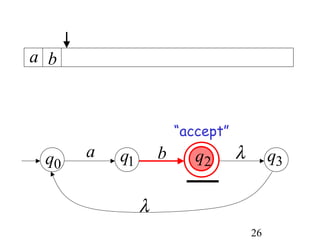
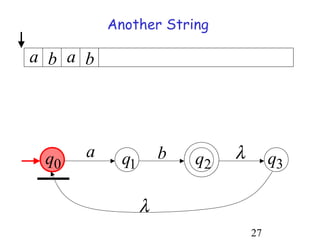
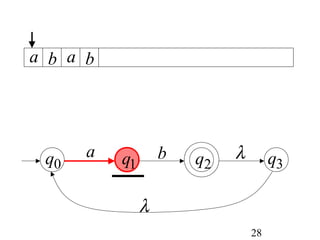
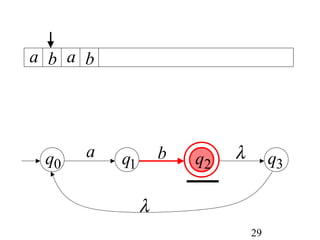
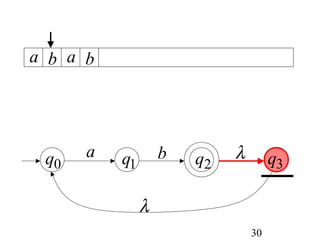
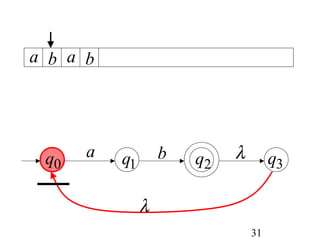
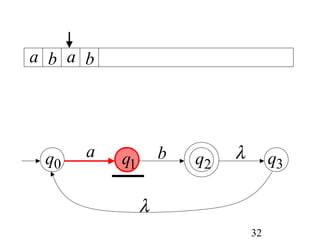
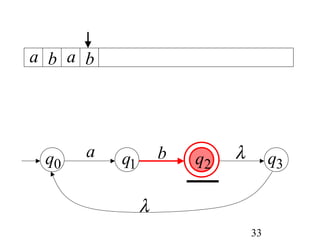
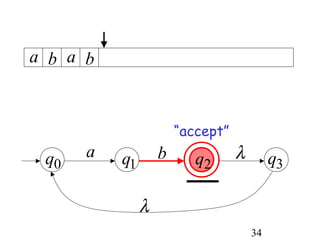
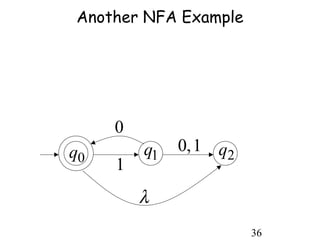
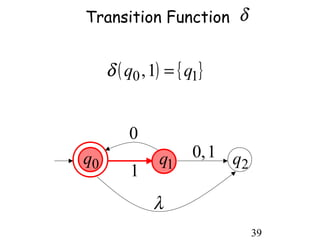
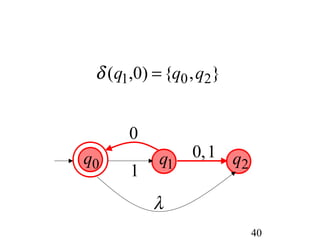
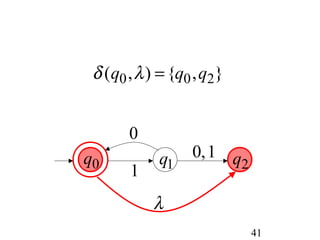
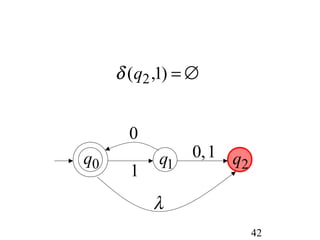
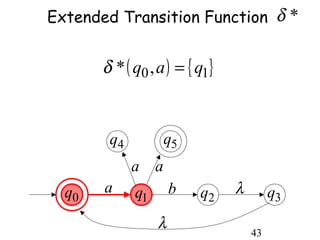
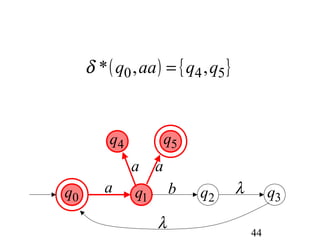
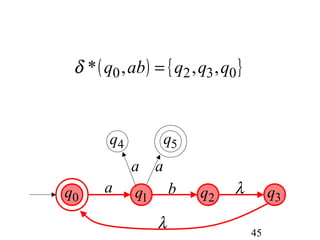
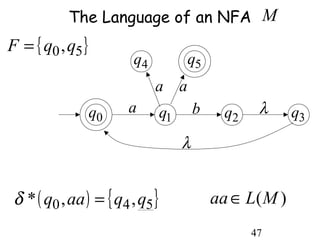
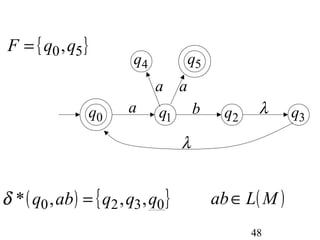
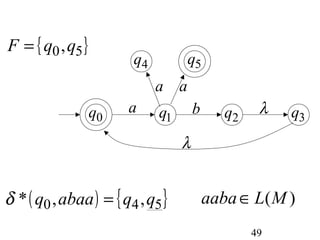
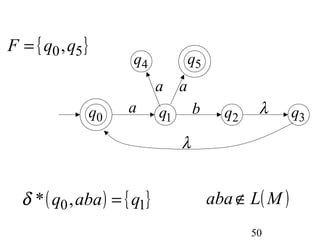
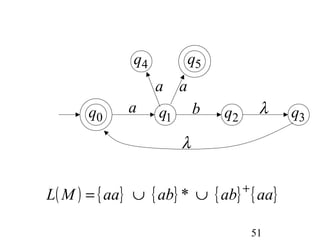
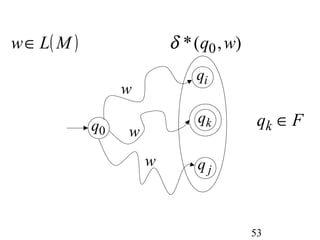
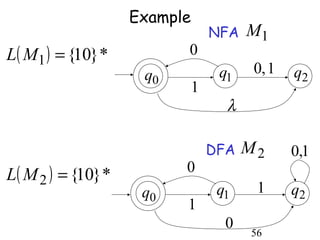
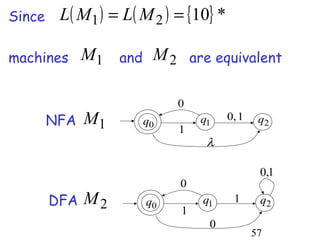
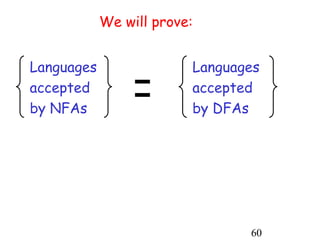
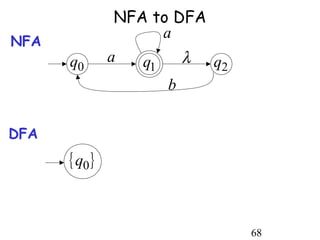
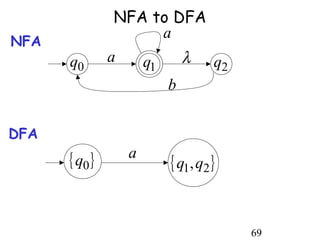
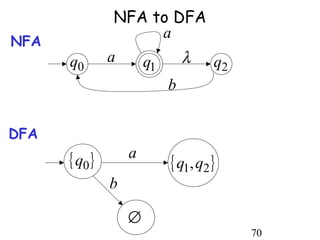
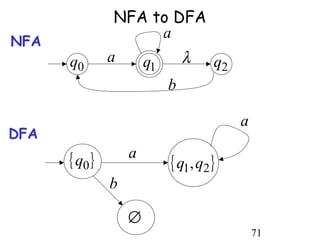
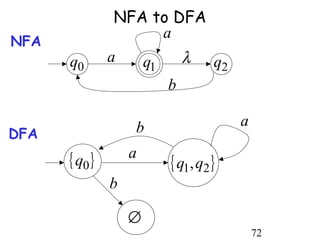
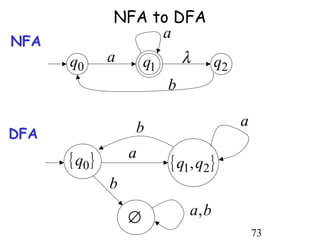
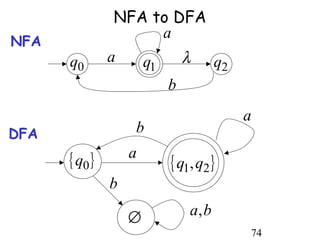
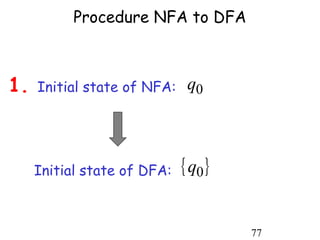
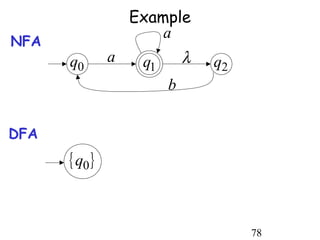
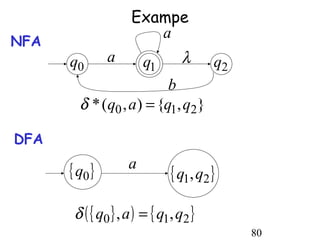
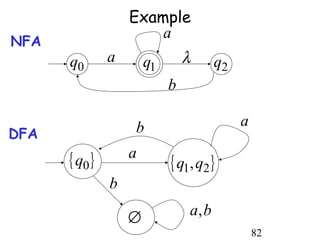
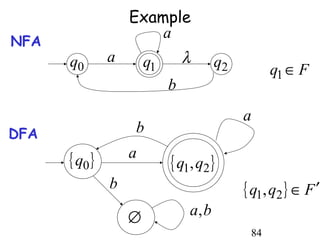
This document describes non-deterministic finite automata (NFAs). It begins by presenting examples of NFAs with different transition diagrams and explanations. It then provides a formal definition of NFAs, including their components like states, alphabet, transition function, initial state, and final states. The document explains how the transition function works and how to determine the language accepted by an NFA using the extended transition function. It proves that NFAs and deterministic finite automata (DFAs) are equivalent by showing that the languages accepted by each are equal subsets of each other. Finally, it demonstrates how to convert an NFA to an equivalent DFA by constructing the DFA states as power sets of the NFA states and defining

1. Non Deterministic Automata
1

2. Nondeterministic Finite Accepter (NFA)
Alphabet = {a}
q1 a q2
a
q0
a
q3
2

3. Nondeterministic Finite Accepter (NFA)
Alphabet = {a}
Two choices q1 a q2
a
q0
a
q3
3

4. Nondeterministic Finite Accepter (NFA)
Alphabet = {a}
Two choices q1 a q2 No transition
a
q0
a
q3 No transition
4

5. First Choice
a a
q1 a q2
a
q0
a
q3
5

6. First Choice
a a
q1 a q2
a
q0
a
q3
6

7. First Choice
a a
q1 a q2
a
q0
a
q3
7

8. First Choice
a a
q1 a q2 “accept”
a
q0
a
q3
8

9. Second Choice
a a
q1 a q2
a
q0
a
q3
9

10. Second Choice
a a
q1 a q2
a
q0
a
q3
10

11. Second Choice
a a
q1 a q2
a
q0
a
No transition:
q3
the automaton hangs
11

12. Second Choice
a a
q1 a q2
a
q0
a
q3 “reject”
12

13. Observation
An NFA accepts a string
if
there is a computation of the NFA
that accepts the string
13

14. Example
aa is accepted by the NFA:
q1 a q2
a
q0
a
q3
14

15. Lambda Transitions
q0 a q1 λ q1 a q3
15

16. a a
q0 a q1 λ q2 a q3
16

17. a a
q0 a q1 λ q2 a q3
17

18. (read head doesn’t move)
a a
q0 a q1 λ q2 a q3
18

19. a a
q0 a q1 λ q2 a q3
19

20. a a
“accept”
q0 a q1 λ q2 a q3
String aa is accepted
20

21. Language accepted: L = {aa}
q0 a q1 λ q2 a q3
21

22. Another NFA Example
q0 a q1 b q2 λ q3
λ
22

23. a b
q0 a q1 b q2 λ q3
λ
23

24. a b
q0 a q1 b q2 λ q3
λ
24

25. a b
q0 a q1 b q2 λ q3
λ
25

26. a b
“accept”
q0 a q1 b q2 λ q3
λ
26

27. Another String
a b a b
q0 a q1 b q2 λ q3
λ
27

28. a b a b
q0 a q1 b q2 λ q3
λ
28

29. a b a b
q0 a q1 b q2 λ q3
λ
29

30. a b a b
q0 a q1 b q2 λ q3
λ
30

31. a b a b
q0 a q1 b q2 λ q3
λ
31

32. a b a b
q0 a q1 b q2 λ q3
λ
32

33. a b a b
q0 a q1 b q2 λ q3
λ
33

34. a b a b
“accept”
q0 a q1 b q2 λ q3
λ
34

35. Language accepted
L = { ab, abab, ababab, ...}
+
= { ab}
q0 a q1 b q2 λ q3
λ
35

36. Another NFA Example
0
q0 q1 0, 1 q2
1
λ
36

37. Language accepted
L = { λ , 10, 1010, 101010, ...}
= {10} *
0
q0 q1 0, 1 q2
1
λ
37

38. Formal Definition of NFAs
M = ( Q, Σ, δ , q0 , F )
Q : Set of states, i.e. { q0 , q1, q2 }
Σ : Input aplhabet, i.e. { a, b}
δ: Transition function
q0 : Initial state
F : Final states
38

39. Transition Function δ
δ ( q0 , 1) = { q1}
0
q0 q1 0, 1 q
2
1
λ
39

40. δ (q1,0) = {q0 , q2 }
0
q0 q1 0, 1 q
2
1
λ
40

41. δ (q0 , λ ) = {q0 , q2 }
0
q0 q1 0, 1 q
2
1
λ
41

42. δ (q2 ,1) = ∅
0
q0 q1 0, 1 q
2
1
λ
42

43. Extended Transition Function δ *
δ * ( q0 , a ) = { q1}
q4 q5
a a
q0 a q1 b q2 λ q3
λ
43

44. δ * ( q0 , aa ) = { q4 , q5 }
q4 q5
a a
q0 a q1 b q2 λ q3
λ
44

45. δ * ( q0 , ab ) = { q2 , q3 , q0 }
q4 q5
a a
q0 a q1 b q2 λ q3
λ
45

46. Formally
It holds q j ∈ δ * ( qi , w)
if and only if
there is a walk from qi to q j
with label w
46

47. The Language of an NFA M
F = { q0 ,q5 }
q4 q5
a a
q0 a q1 b q2 λ q3
λ
δ * ( q0 , aa ) = { q4 , q5 } aa ∈ L(M )
47

48. F = { q0 ,q5 }
q4 q5
a a
q0 a q1 b q2 λ q3
λ
δ * ( q0 , ab ) = { q2 , q3 , q0 } ab ∈ L( M )
48

49. F = { q0 ,q5 }
q4 q5
a a
q0 a q1 b q2 λ q3
λ
δ * ( q0 , abaa ) = { q4 , q5 } aaba ∈ L(M )
49

50. F = { q0 ,q5 }
q4 q5
a a
q0 a q1 b q2 λ q3
λ
δ * ( q0 , aba ) = { q1} aba ∉ L( M )
50

51. q4 q5
a a
q0 a q1 b q2 λ q3
λ
+
L( M ) = { aa} ∪ { ab} * ∪ { ab} { aa}
51

52. Formally
The language accepted by NFA M is:
L( M ) = { w1, w2 , w3 ,...}
where δ * (q0 , wm ) = {qi , q j ,...}
and there is some qk ∈ F (final state)
52

53. w∈ L( M ) δ * (q0 , w)
qi
w
q0
qk qk ∈ F
w
w qj
53

54. Equivalence of NFAs and DFAs
54

55. Equivalence of Machines
For DFAs or NFAs:
Machine M1 is equivalent to machine M 2
if L( M 1 ) = L( M 2 )
55

56. Example
NFA M1
L( M1 ) = {10} * 0
q0 q1 0, 1 q2
1
λ
DFA M2 0,1
0
L( M 2 ) = {10} *
q0 q1 1 q2
1
0
56

57. Since L( M1 ) = L( M 2 ) = {10} *
machines M1 and M 2 are equivalent
0
NFA M1 q0 q1 0, 1 q2
1
λ
0,1
0
DFA M2 q0 q1 1 q2
1
0
57

58. Equivalence of NFAs and DFAs
Question: NFAs = DFAs ?
Same power?
Accept the same languages?
58

59. Equivalence of NFAs and DFAs
Question: NFAs = DFAs ? YES!
Same power?
Accept the same languages?
59

60. We will prove:
=
Languages Languages
accepted accepted
by NFAs by DFAs
60

61. We will prove:
=
Languages Languages
accepted accepted
by NFAs by DFAs
NFAs and DFAs have the same
computation power
61

62. Step 1
Languages Languages
accepted ⊇ accepted
by NFAs by DFAs
62

63. Step 1
Languages Languages
accepted ⊇ accepted
by NFAs by DFAs
Proof: Every DFA is also an NFA
63

64. Step 1
Languages Languages
accepted ⊇ accepted
by NFAs by DFAs
Proof: Every DFA is also an NFA
A language accepted by a DFA
is also accepted by an NFA
64

65. Step 2
Languages Languages
accepted ⊆ accepted
by NFAs by DFAs
65

66. Step 2
Languages Languages
accepted ⊆ accepted
by NFAs by DFAs
Proof: Any NFA can be converted to an
equivalent DFA
66

67. Step 2
Languages Languages
accepted ⊆ accepted
by NFAs by DFAs
Proof: Any NFA can be converted to an
equivalent DFA
A language accepted by an NFA
is also accepted by a DFA 67

68. NFA to DFA
a
NFA
q0 a q1 λ q2
b
DFA
{ q0 }
68

69. NFA to DFA
a
NFA
q0 a q1 λ q2
b
DFA
{ q0 } a
{ q1, q2 }
69

70. NFA to DFA
a
NFA
q0 a q1 λ q2
b
DFA
{ q0 } a
{ q1, q2 }
b
∅
70

71. NFA to DFA
a
NFA
q0 a q1 λ q2
b
a
DFA
{ q0 } a
{ q1, q2 }
b
∅
71

72. NFA to DFA
a
NFA
q0 a q1 λ q2
b
b a
DFA
{ q0 } a
{ q1, q2 }
b
∅
72

73. NFA to DFA
a
NFA
q0 a q1 λ q2
b
b a
DFA
{ q0 } a
{ q1, q2 }
b
∅ a, b
73

74. NFA to DFA
a
NFA
q0 a q1 λ q2
b
a
DFA b
{ q0 } a
{ q1, q2 }
b
∅ a, b
74

75. NFA to DFA: Remarks
We are given an NFA M
We want to convert it
to an equivalent DFA M ′
With L( M ) = L(M ′)
75

76. If the NFA has states
q0 , q1, q2 ,...
the DFA has states in the powerset
∅, { q0 } , { q1} , { q1, q2 } , { q3 , q4 , q7 } ,....
76

77. Procedure NFA to DFA
1. Initial state of NFA: q0
Initial state of DFA: { q0 }
77

78. Example
a
NFA
q0 a q1 λ q2
b
DFA
{ q0 }
78

79. Procedure NFA to DFA
2. For every DFA’s state {qi , q j ,..., qm }
Compute in the NFA
δ * ( qi , a ) ,
δ * ( q j , a ), = {qi′ , q′j ,..., qm }
′
...
Add transition
δ ({qi , q j ,..., qm }, a ) = {qi′ , q′j ,..., qm }
′
79

80. Exampe
a
NFA
q0 a q1 λ q2
b
δ * (q0 , a ) = {q1, q2}
DFA
{ q0 } a
{ q1, q2 }
δ ( { q0 } , a ) = { q1, q2 }
80

81. Procedure NFA to DFA
Repeat Step 2 for all letters in alphabet,
until
no more transitions can be added.
81

82. Example
a
NFA
q0 a q1 λ q2
b
b a
DFA
{ q0 } a
{ q1, q2 }
b
∅ a, b
82

83. Procedure NFA to DFA
3. For any DFA state {qi , q j ,..., qm }
If some q j is a final state in the NFA
Then, {qi , q j ,..., qm }
is a final state in the DFA
83

84. Example
a
NFA
q0 a q1 λ q2 q1 ∈ F
b
a
DFA b
{ q0 } a
{ q1, q2 }
b { q1, q2 } ∈ F ′
∅ a, b
84

85. Theorem
Take NFA M
Apply procedure to obtain DFA M′
Then M and M′ are equivalent :
L( M ) = L( M ′)
85

86. Finally
We have proven
=
Languages Languages
accepted accepted
by NFAs by DFAs
86

87. We have proven
=
Languages Languages
accepted accepted
by NFAs by DFAs
Regular Languages
87

88. We have proven
=
Languages Languages
accepted accepted
by NFAs by DFAs
Regular Languages Regular Languages
88