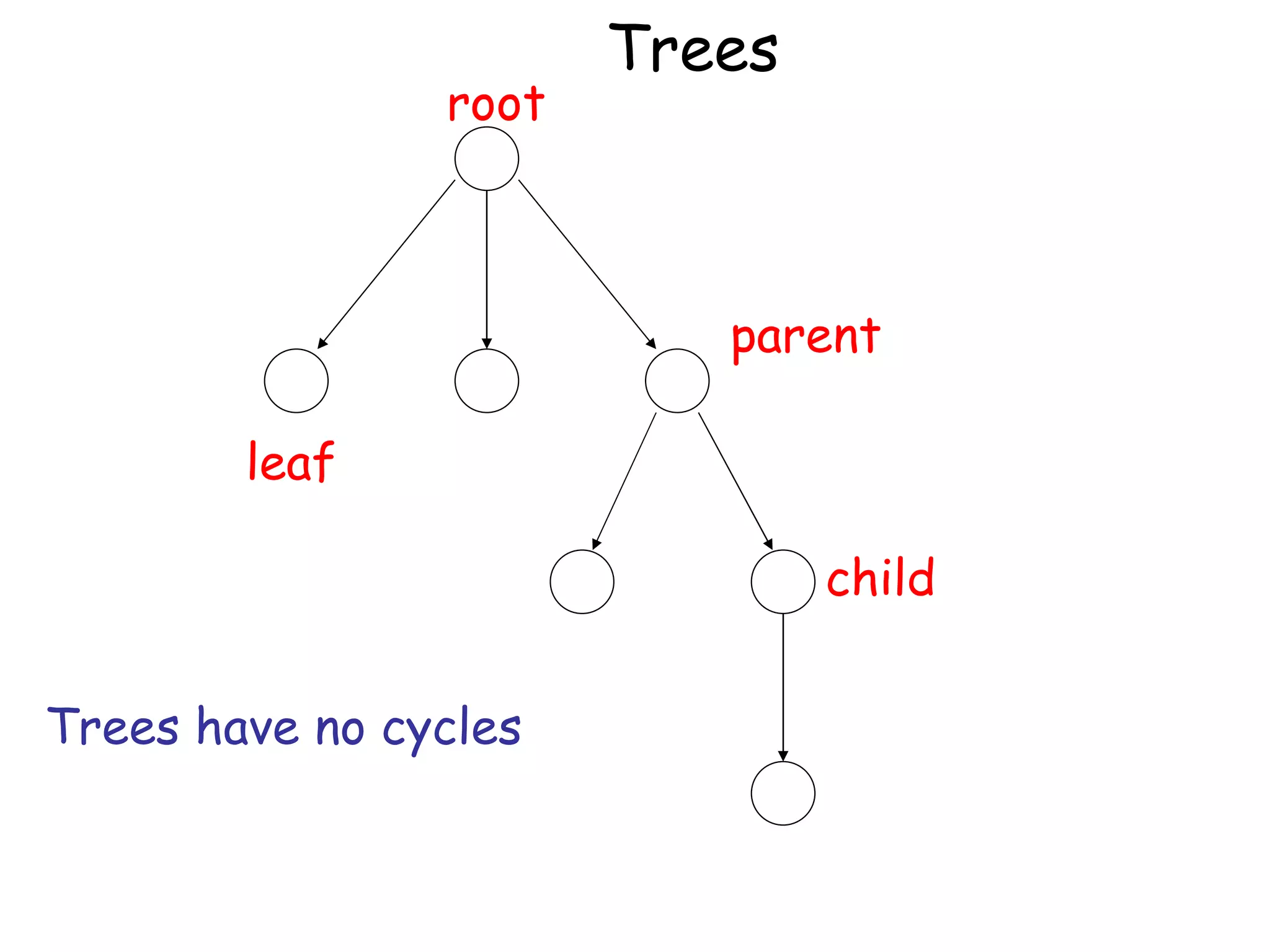
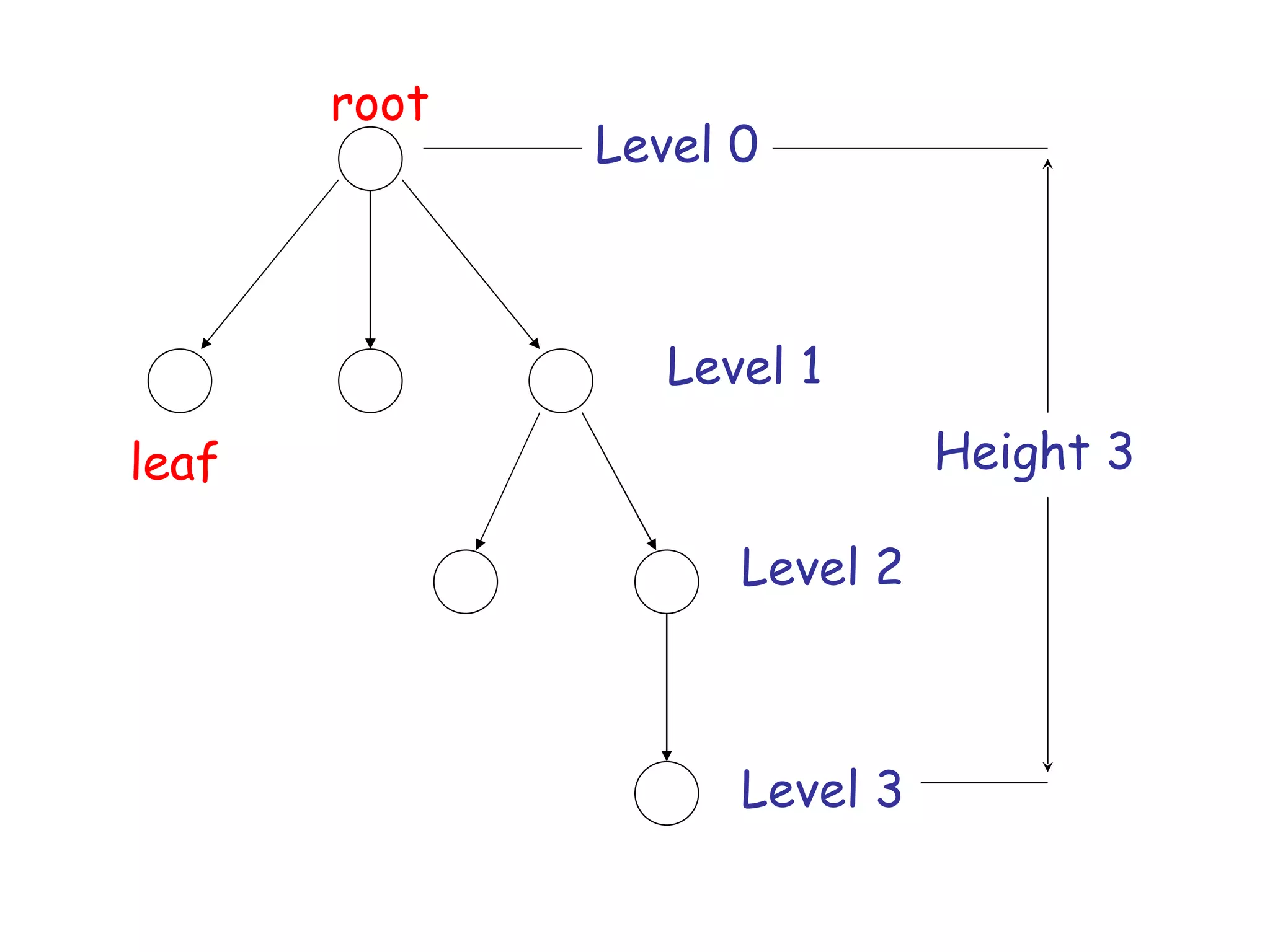
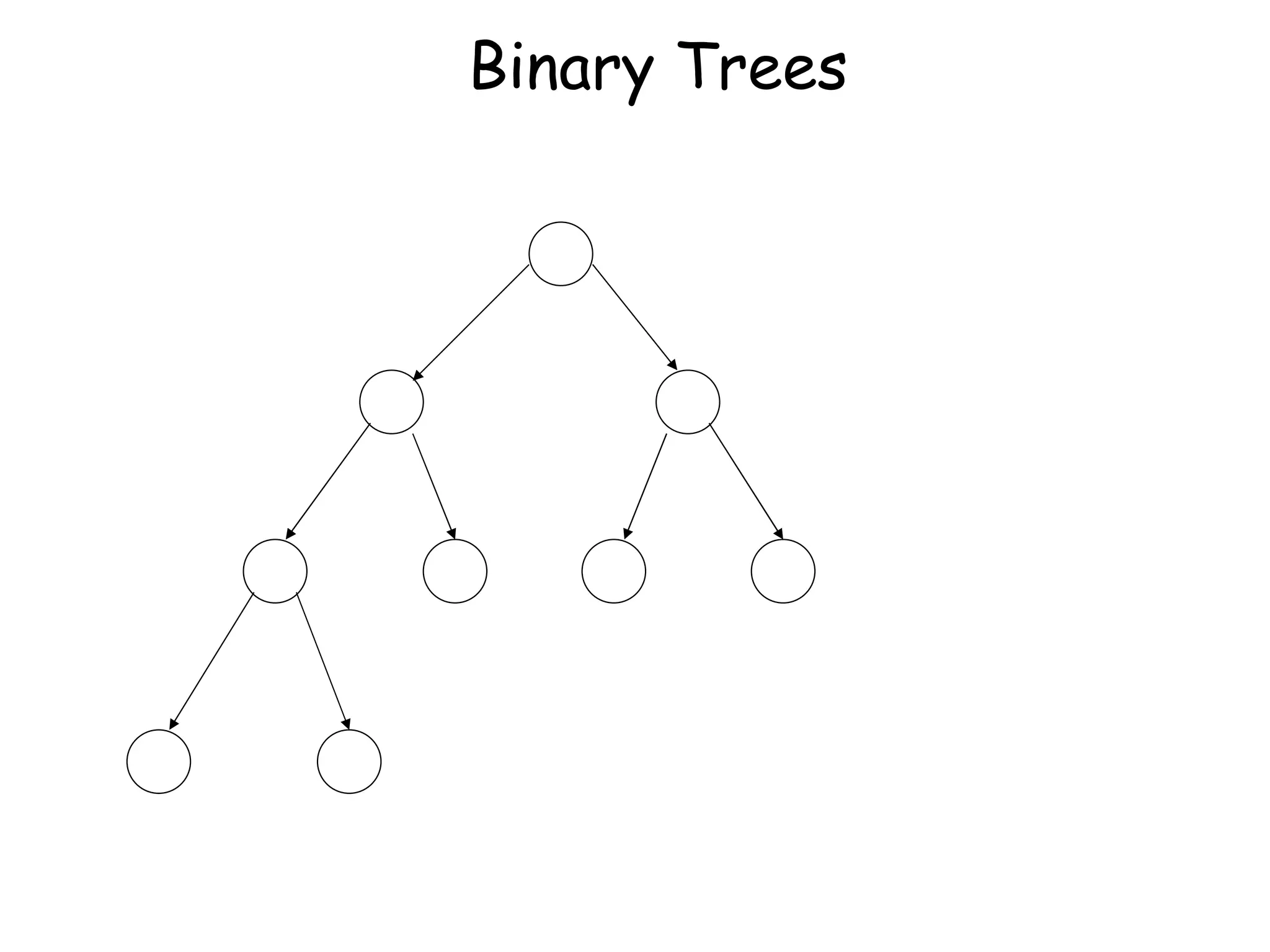
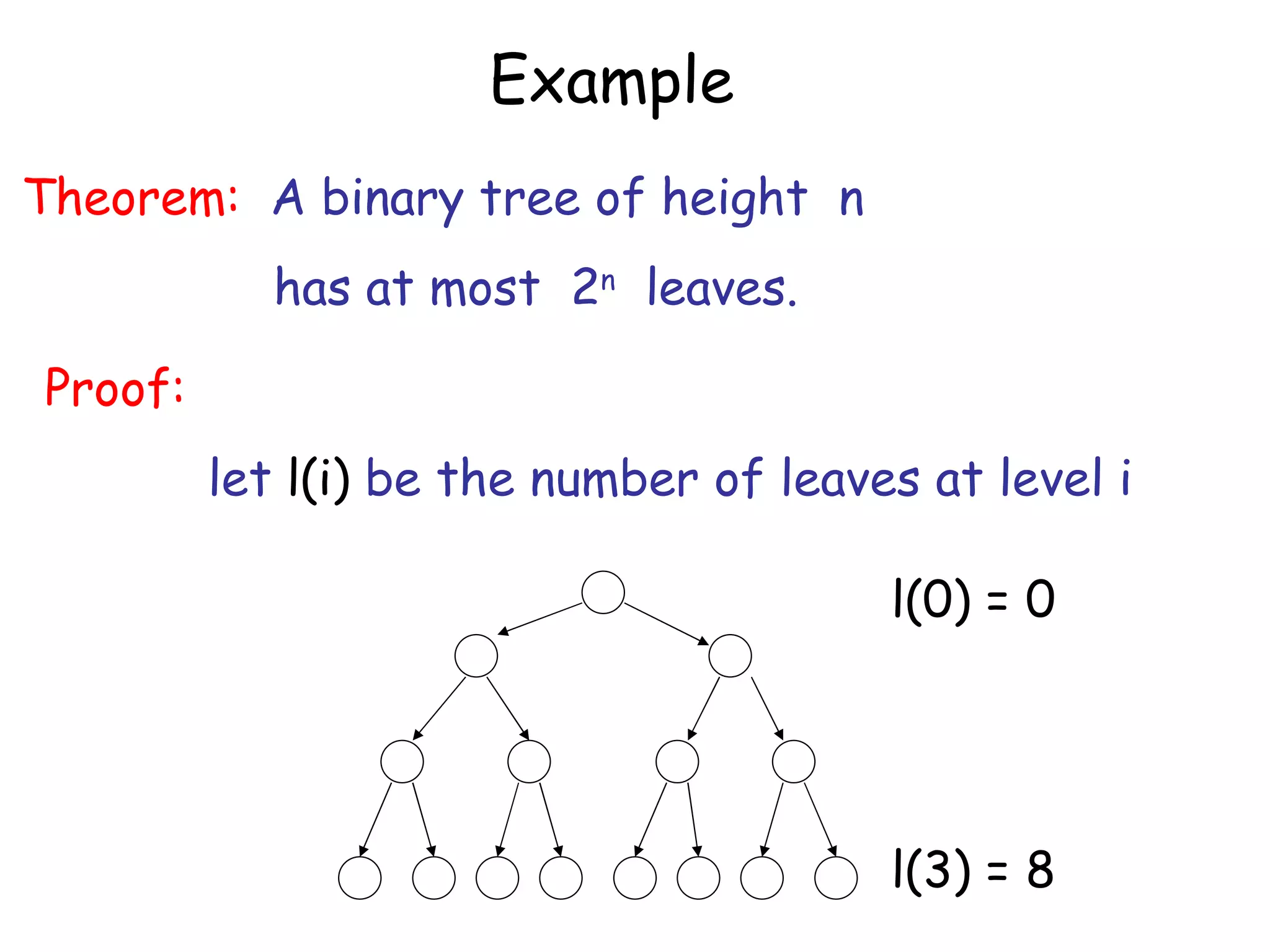
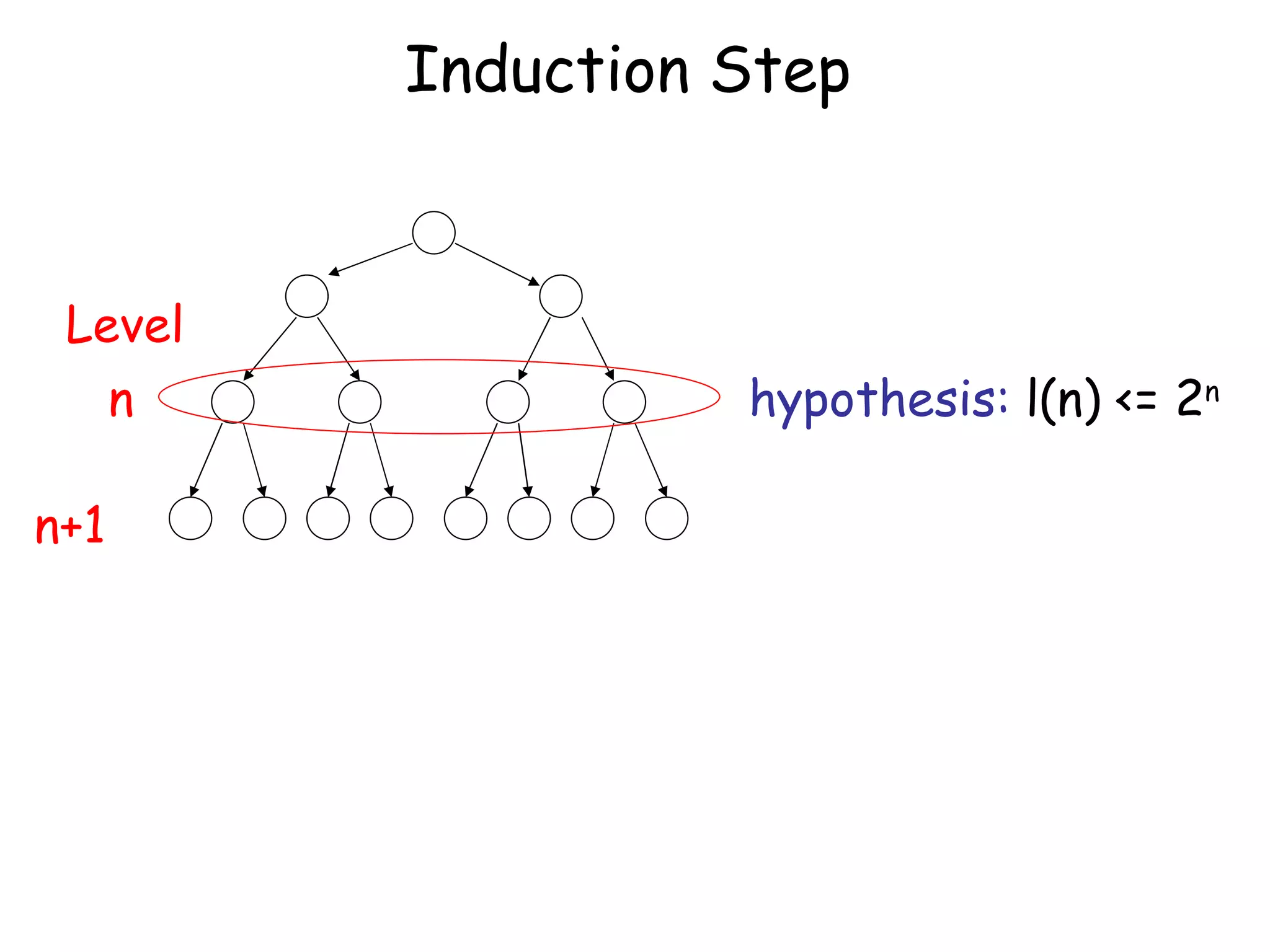
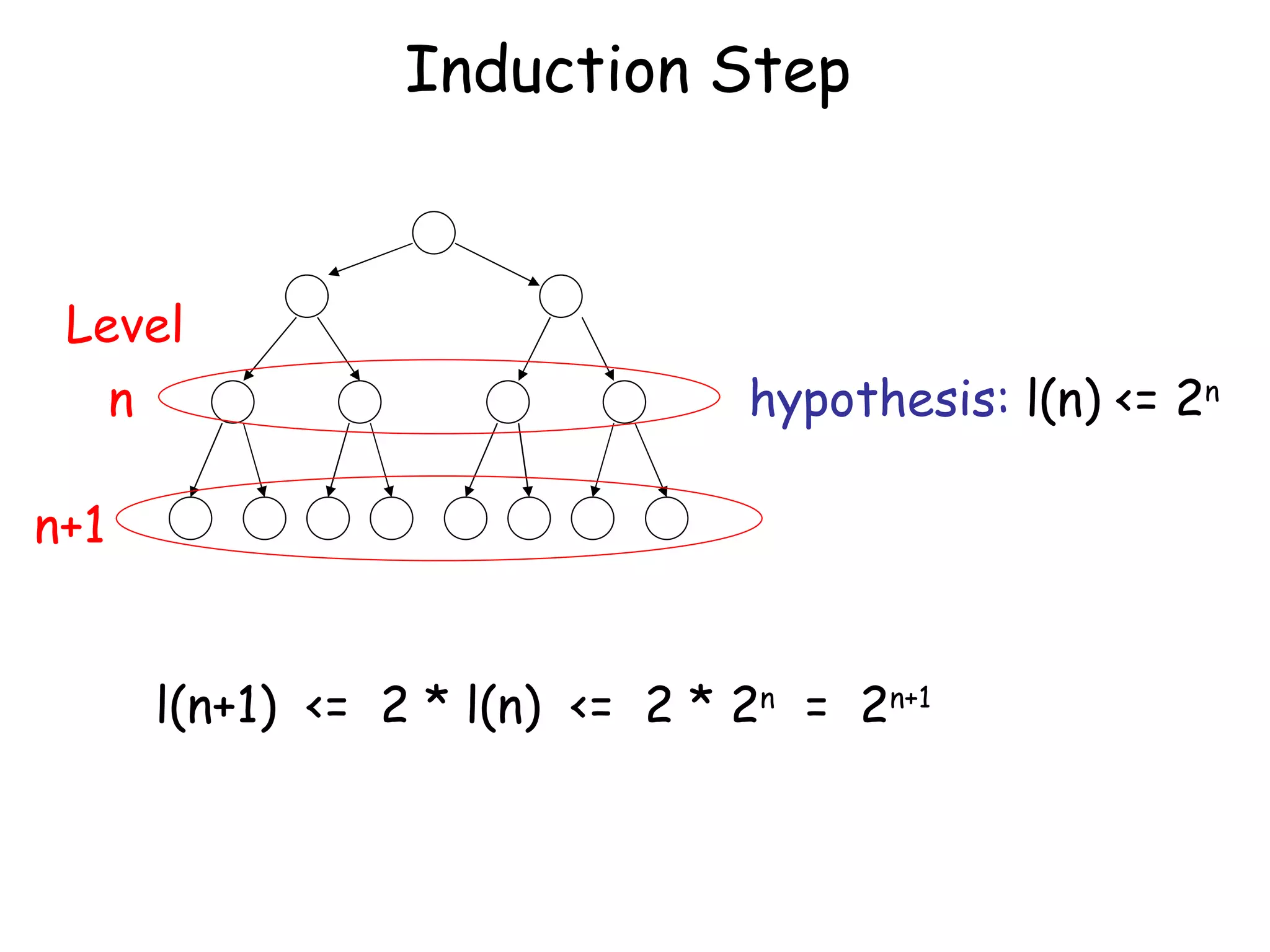
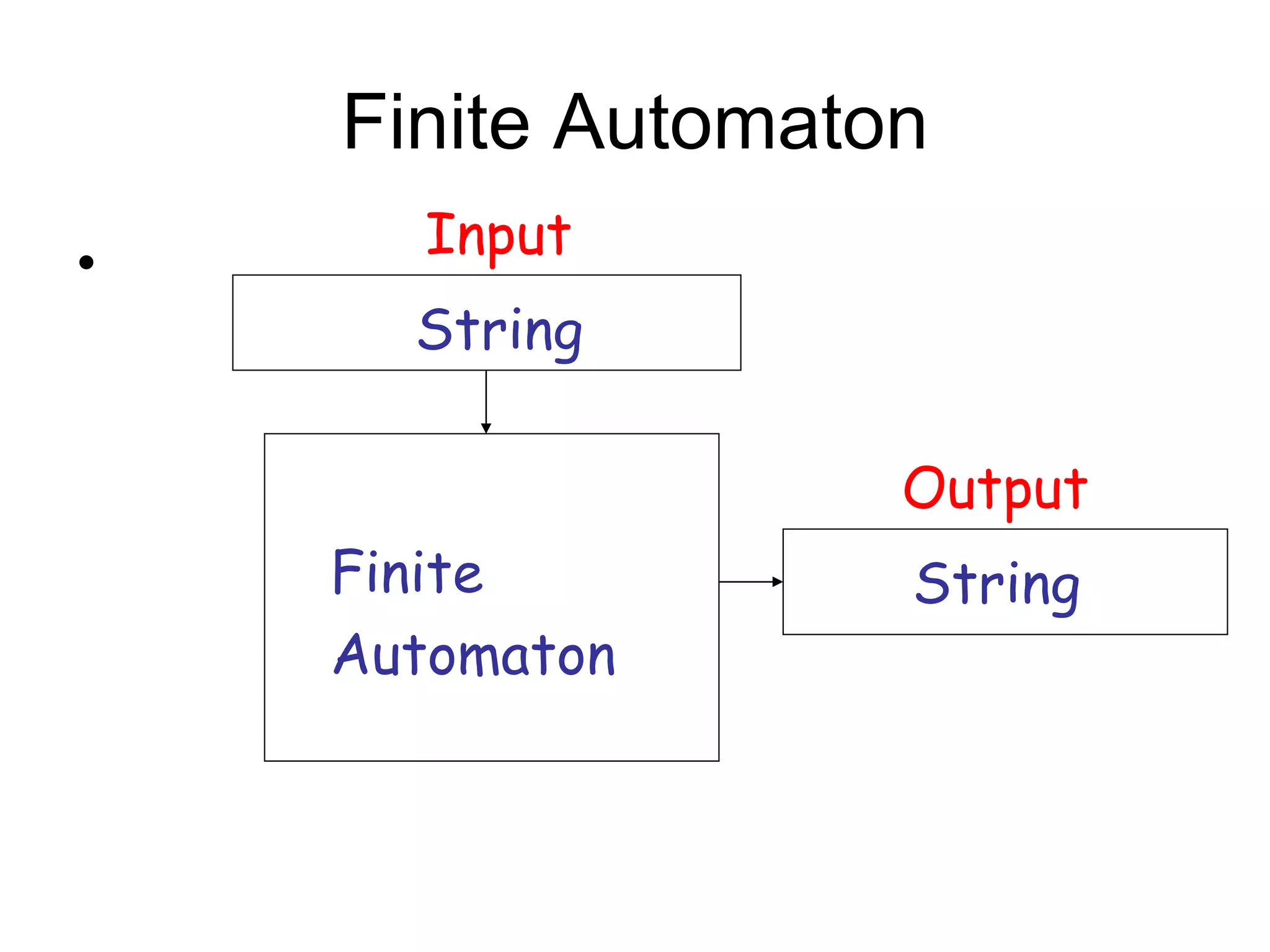
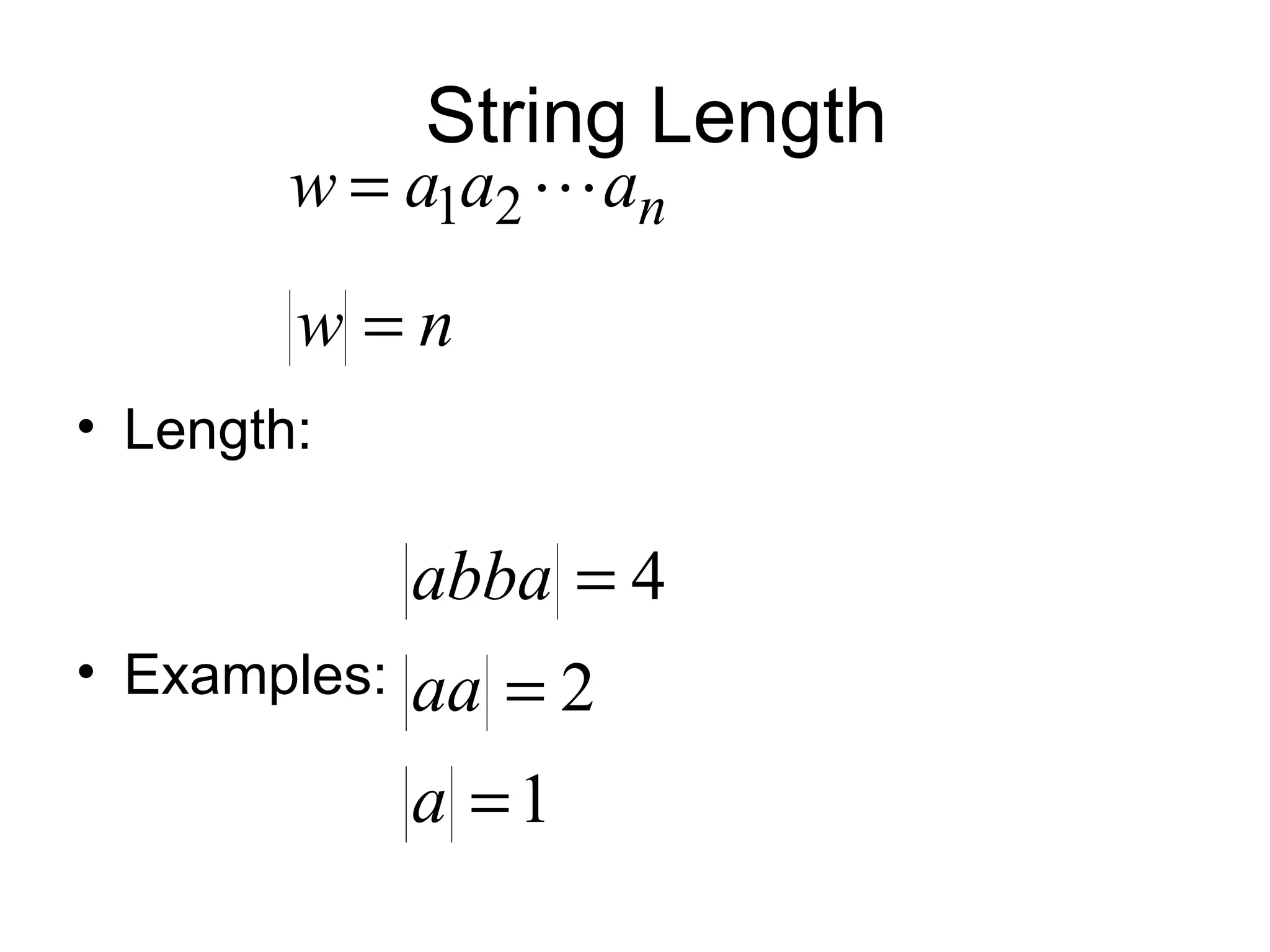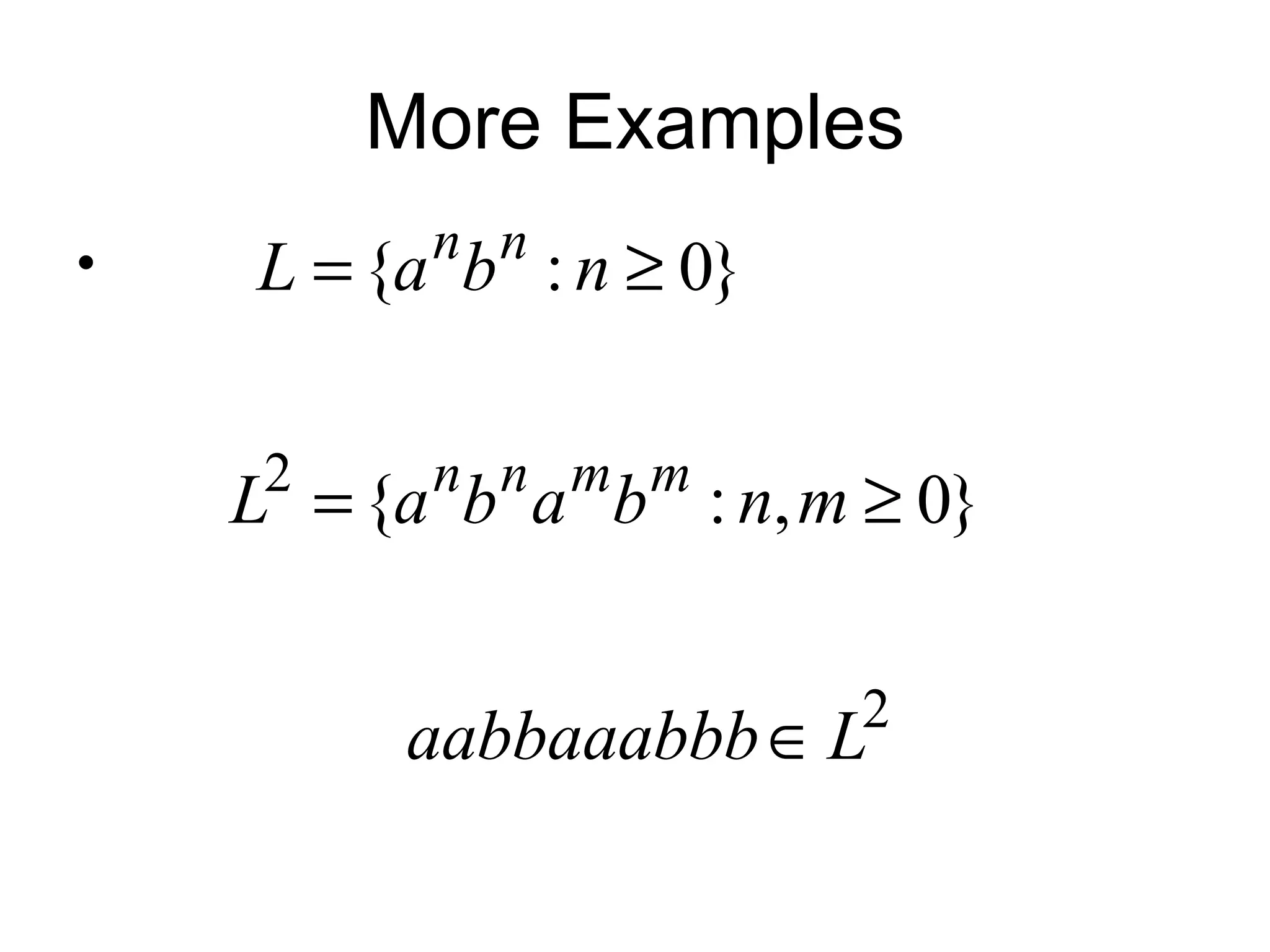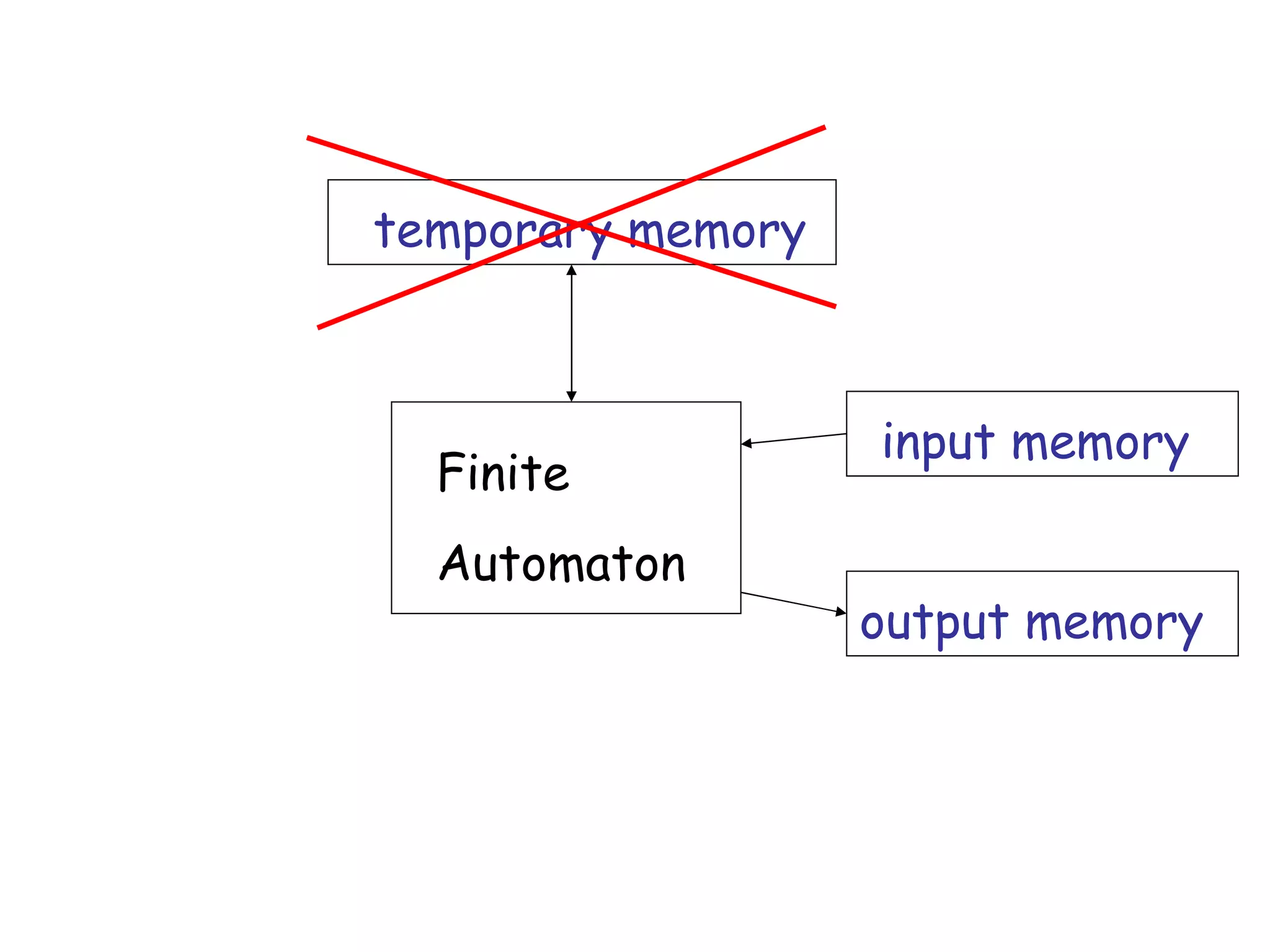
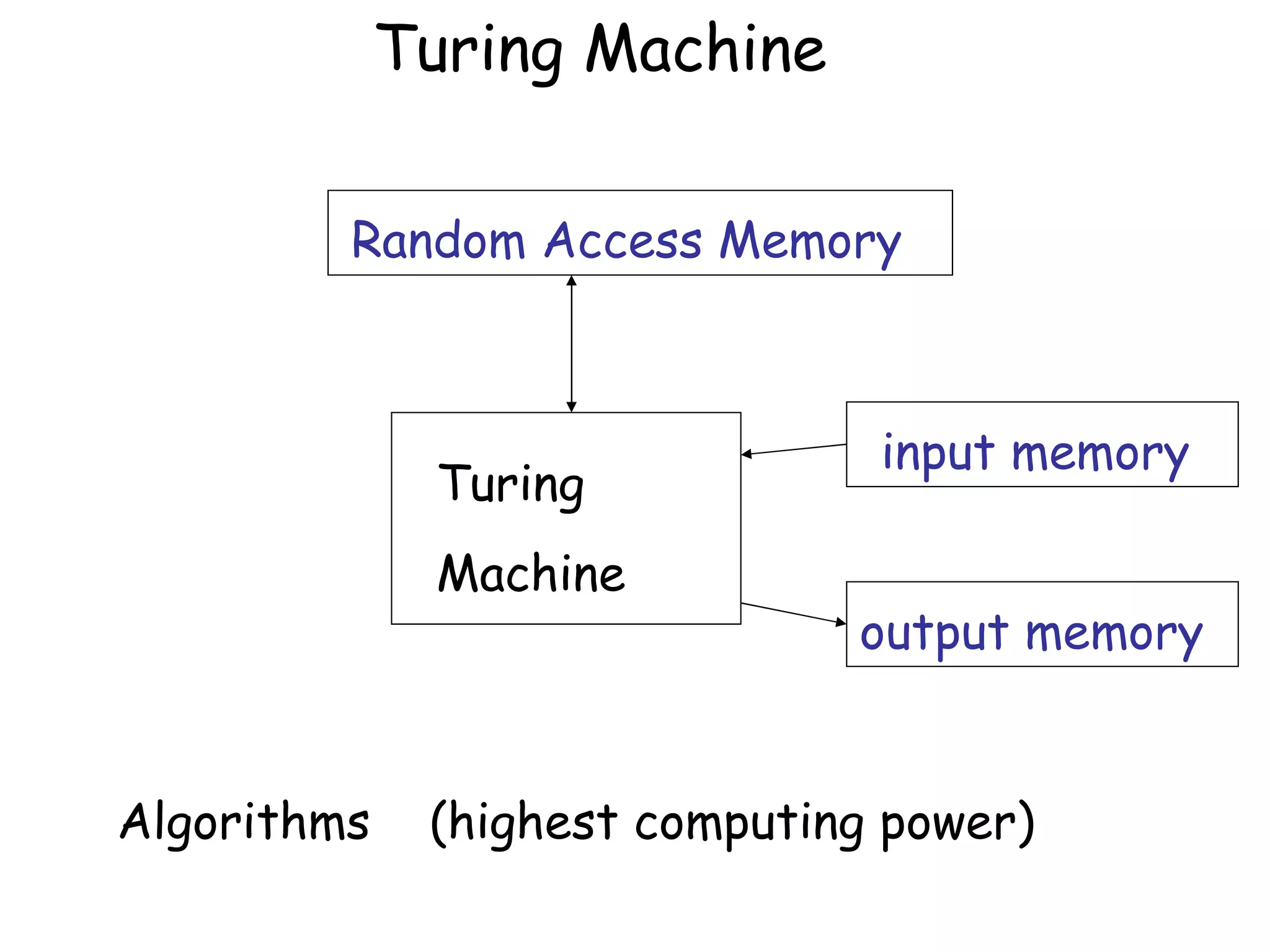
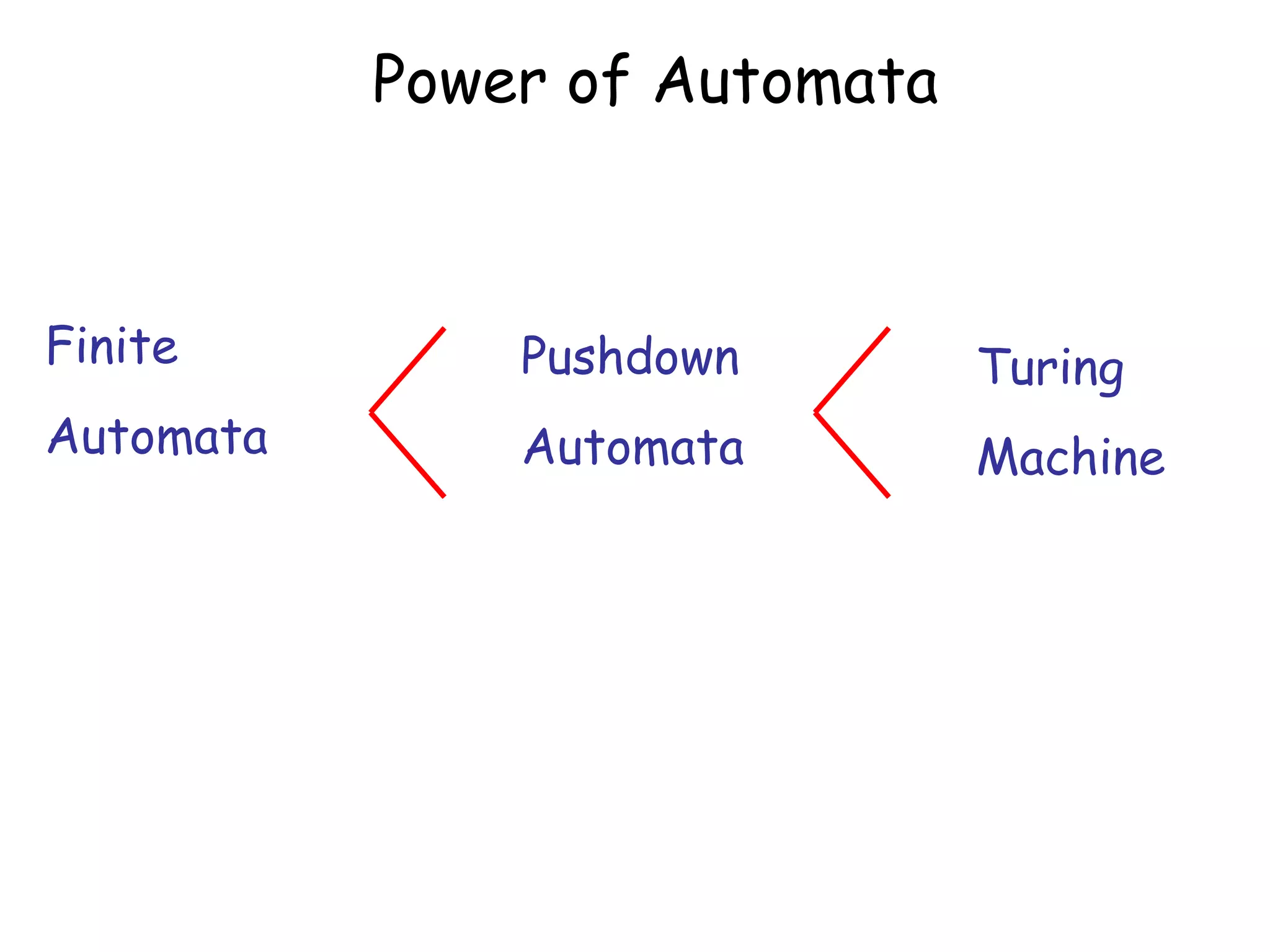
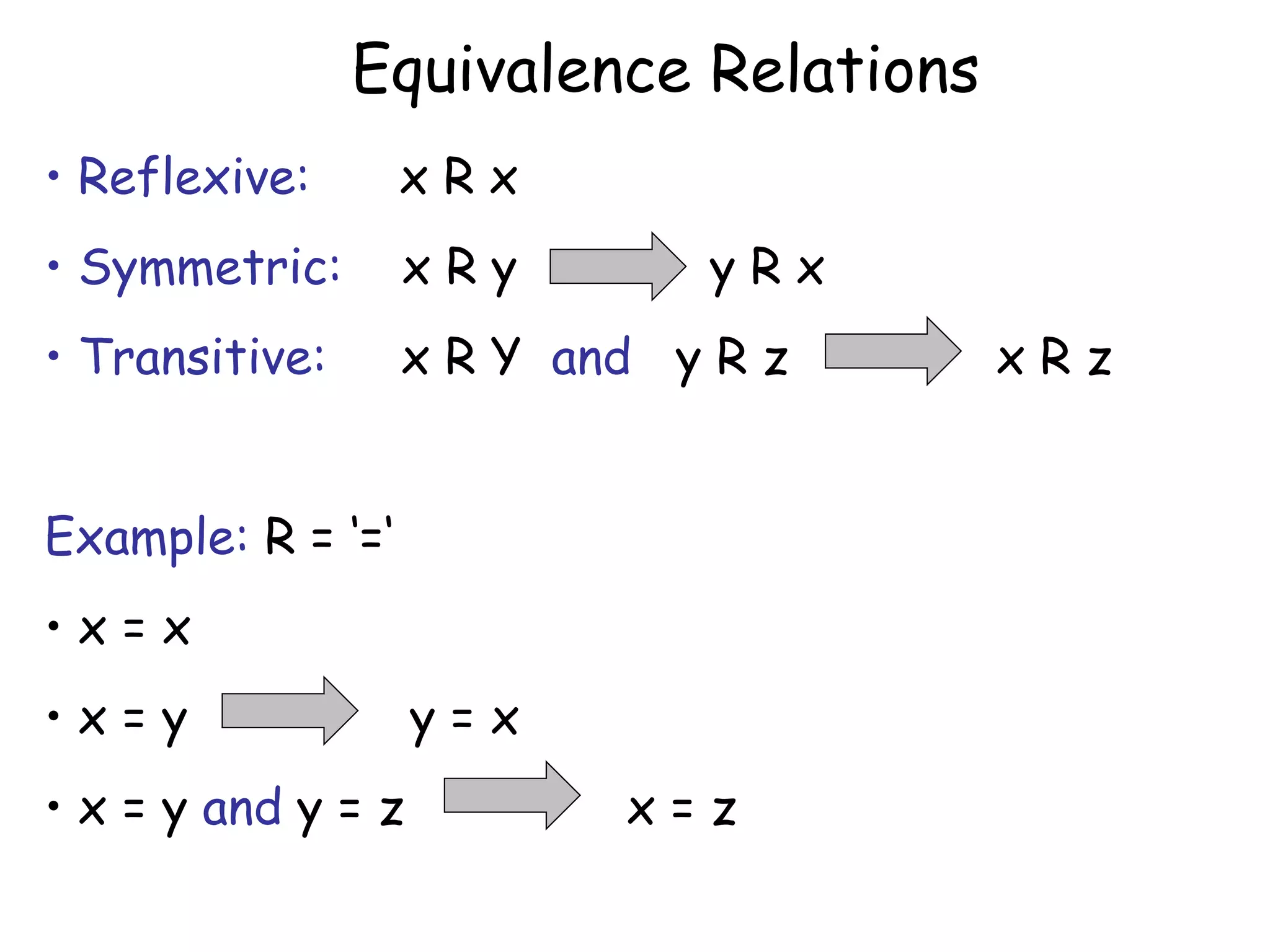
The document discusses the theory of automata and formal languages including: - Different types of automata like finite automata, pushdown automata, and Turing machines. - Context-free grammars and properties of regular, context-free, and recursively enumerable languages. - Operations on strings and languages like concatenation, Kleene closure, and positive closure. - Proofs techniques like proof by induction and proof by contradiction.

1. Theory of Automata
&
Formal Languages

2. BOOKS
Theory of computer Science: K.L.P.Mishra &
N.Chandrasekharan
Intro to Automata theory, Formal languages and
computation: Ullman,Hopcroft
Motwani
Elements of theory of computation Lewis &
papadimitrou

3. Syllabus
Introduction
Deterministic and non deterministic Finite
Automata, Regular Expression,Two way
finite automata,Finite automata with
output,properties of regular sets,pumping
lemma, closure properties,Myhill nerode
theorem

4. Context free Grammar: Derivation trees,
Simplification forms
Pushdown automata: Def, Relationship
between PDA and context free
language,Properties, decision
algorithms
Turing Machines: Turing machine
model,Modification of turing
machines,Church’s
thesis,Undecidability,Recursive and
recursively enumerable languages Post
correspondence problems recursive
functions

5. Chomsky Hierarchy: Regular grammars,
unrestricted grammar, context sensitive
language, relationship among
languages

6. temporary memory
input memory
CPU
output memory
Program memory

7. 3
temporary memory f ( x) = x
z = 2*2 = 4
f ( x) = z * 2 = 8
input memory
x=2
CPU
output memory
Program memory
compute x∗x
2
compute x ∗x

8. Automaton
temporary memory
Automaton
input memory
CPU
output memory
Program memory

9. temporary memory
input memory
Finite
Automaton
output memory

10. Different Kinds of Automata
Automata are distinguished by the temporary memory
• Finite Automata: no temporary memory
• Pushdown Automata: stack
• Turing Machines: random access memory

11. Turing Machine
Random Access Memory
input memory
Turing
Machine
output memory
Algorithms (highest computing power)

12. Power of Automata
Finite Pushdown Turing
Automata Automata Machine

13. Power sets
A power set is a set of sets
S = { a, b, c }
Powerset of S = the set of all the subsets of S
2S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} }
Observation: | 2S | = 2|S| ( 8 = 23 )

14. Cartesian Product
A = { 2, 4 } B = { 2, 3, 5 }
A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 4) }
|A X B| = |A| |B|
Generalizes to more than two sets
AXBX…XZ

15. RELATIONS
R = {(x1, y1), (x2, y2), (x3, y3), …}
xi R yi
e. g. if R = ‘>’: 2 > 1, 3 > 2, 3 > 1
In relations xi can be repeated

16. Equivalence Relations
• Reflexive: xRx
• Symmetric: xRy yRx
• Transitive: x R Y and y R z xRz
Example: R = ‘=‘
•x=x
•x=y y=x
• x = y and y = z x=z

17. Equivalence Classes
For equivalence relation R
equivalence class of x = {y : x R y}
Example:
R = { (1, 1), (2, 2), (1, 2), (2, 1),
(3, 3), (4, 4), (3, 4), (4, 3) }
Equivalence class of 1 = {1, 2}
Equivalence class of 3 = {3, 4}

18. Example of Equivalence relation
Let Z = set of integers
R be defined on it as:
R= {(x,y)| x ∈Z, y ∈ Z and
(x - y)is divisible by
5}
This relation is known as
” congruent modulo 5”

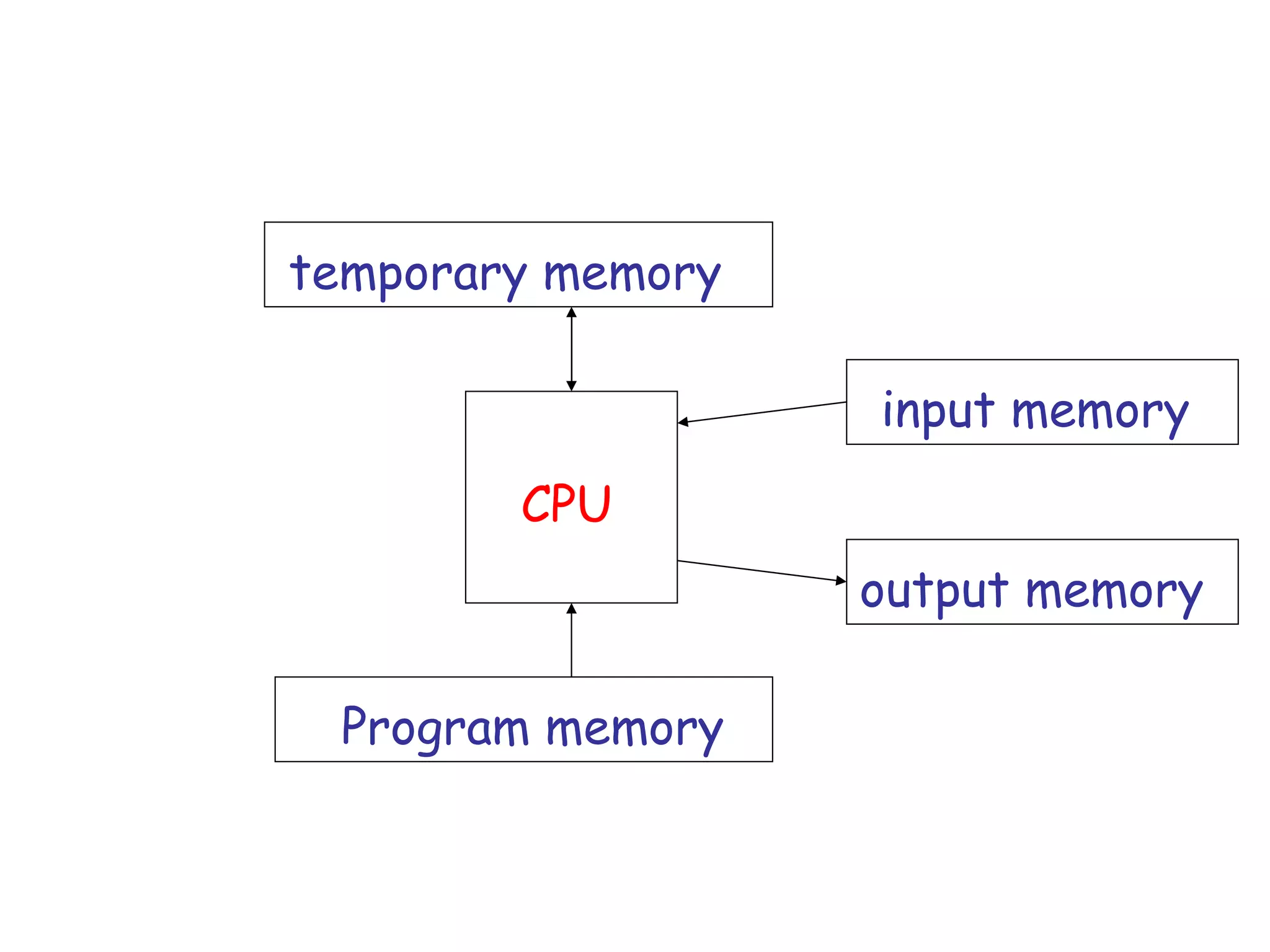
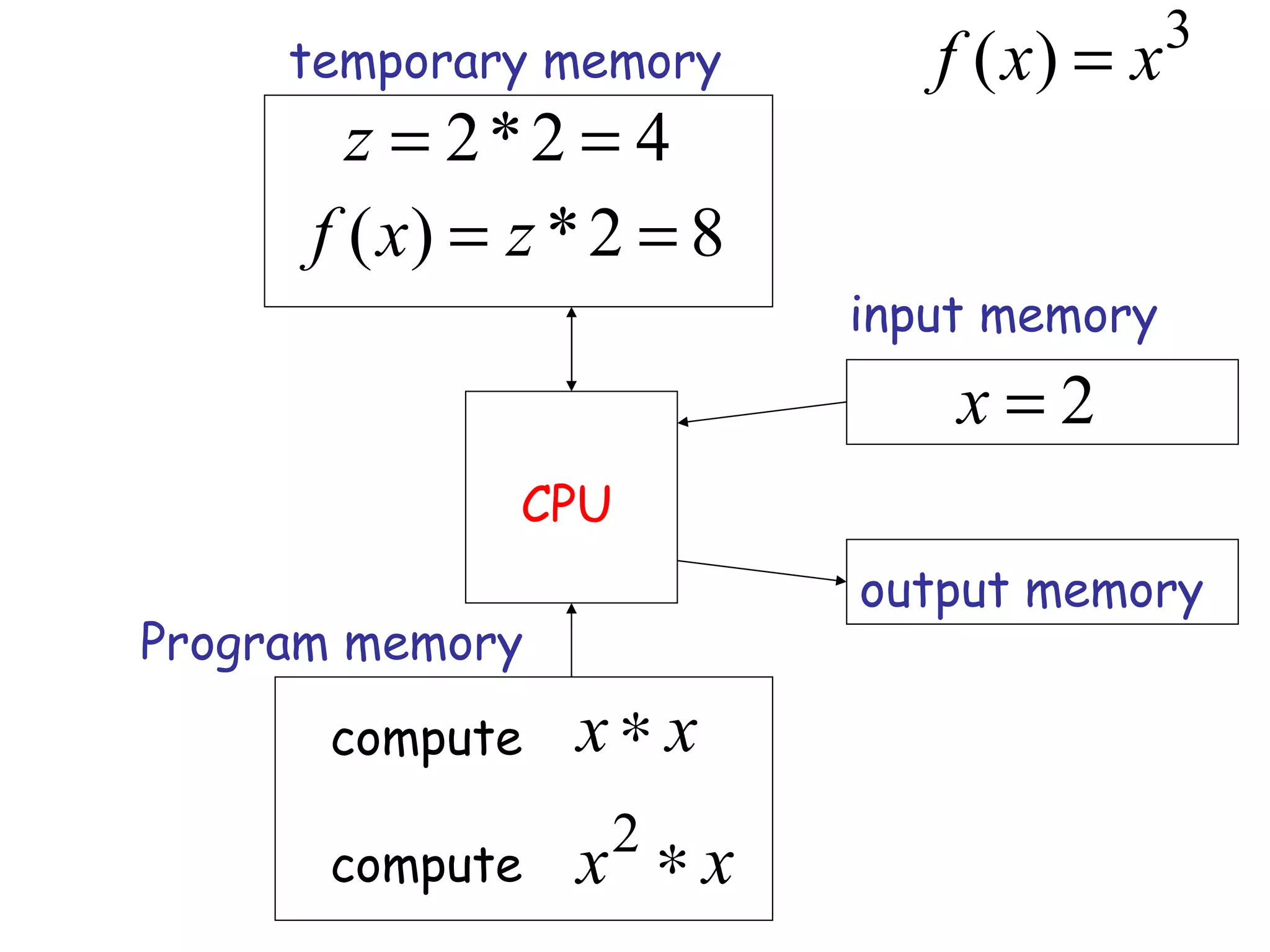
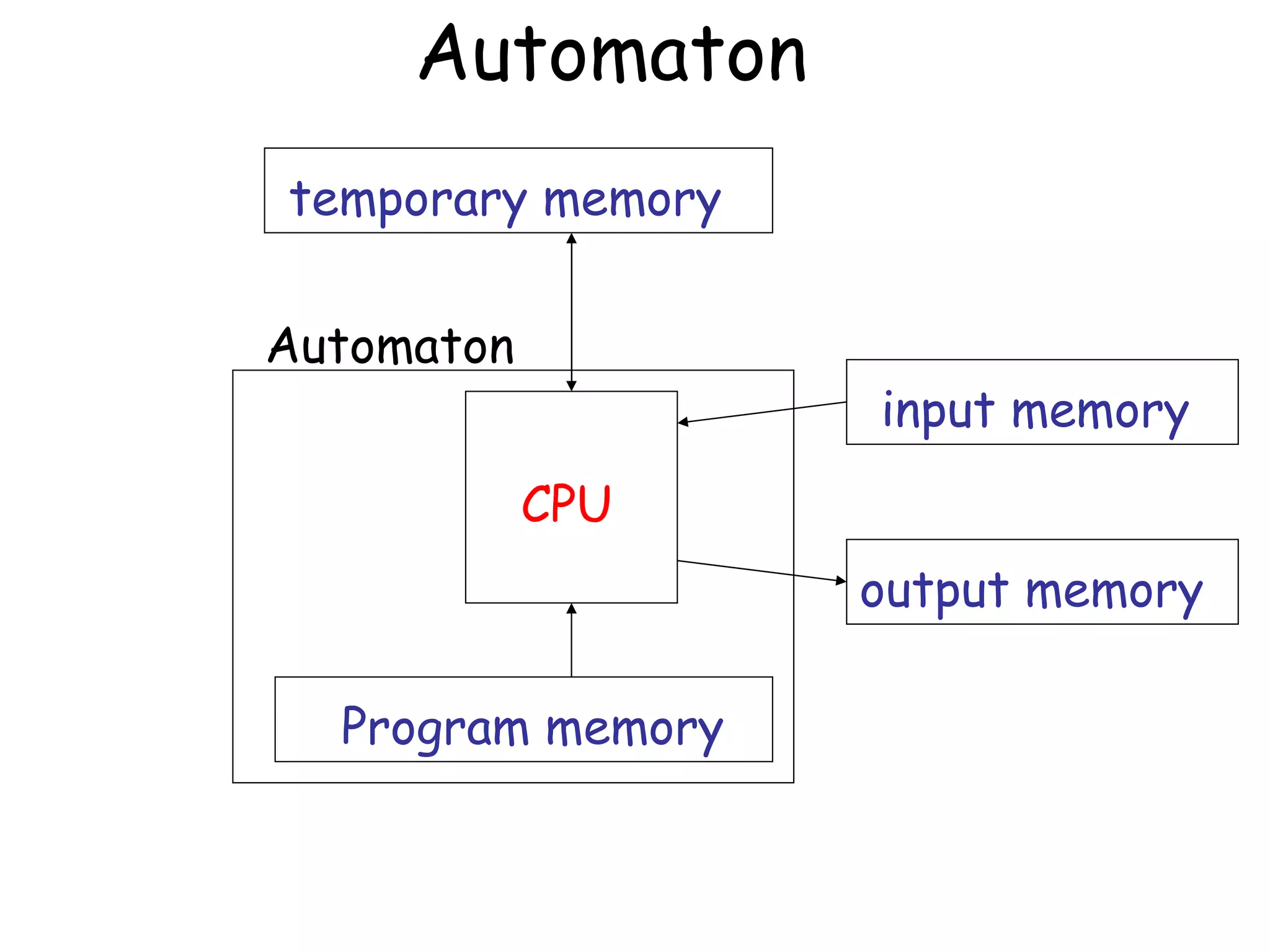
19. The equivalence classes are
[0]R= {…-10, -5, 0, 5,10,…}
[1]R = {…..,-9, -4, 1, 6, 11, 16….}
[2]R= {….-8, -3,2,7,12,17…..}
[3]R = {….-7, -2, 3, 8 ,13,…}
[4]R = {….-6,-1,4,9,14,19,….}
Z/R ={[0]R, [1]R, [2]R, [3]R, [4]R}

20. PROOF TECHNIQUES
• Proof by induction
• Proof by contradiction

21. Induction
We have statements P1, P2, P3, …
If we know
• for some k that P1, P2, …, Pk are true
• for any n >= k that
P1, P2, …, Pn imply Pn+1
Then
Every Pi is true

22. Trees
root
parent
leaf
child
Trees have no cycles

23. Proof by Induction
• Inductive basis
Find P1, P2, …, Pk which are true
• Inductive hypothesis
Let’s assume P1, P2, …, Pn are true,
for any n >= k
• Inductive step
Show that Pn+1 is true

24. root
Level 0
Level 1
leaf Height 3
Level 2
Level 3

25. Binary Trees

26. Example
Theorem: A binary tree of height n
has at most 2n leaves.
Proof:
let l(i) be the number of leaves at level i
l(0) = 0
l(3) = 8

27. Induction Step
Level
n hypothesis: l(n) <= 2n
n+1

28. We want to show: l(i) <= 2i
• Inductive basis
l(0) = 1 (the root node)
• Inductive hypothesis
Let’s assume l(i) <= 2i for all i = 0, 1, …, n
• Induction step
we need to show that l(n + 1) <= 2n+1

29. Induction Step
Level
n hypothesis: l(n) <= 2n
n+1
l(n+1) <= 2 * l(n) <= 2 * 2n = 2n+1

30. Proof by Contradiction
We want to prove that a statement P is true
• we assume that P is false
• then we arrive at an incorrect conclusion
• therefore, statement P must be true

31. Example
Theorem: 2 is not rational
Proof:
Assume by contradiction that it is rational
2 = n/m
n and m have no common factors
We will show that this is impossible

32. 2 = n/m 2 m2 = n2
n is even
Therefore, n2 is even
n=2k
m is even
2 m2 = 4k2 m2 = 2k2
m=2p
Thus, m and n have common factor 2
Contradiction!

33. Basic Terms
Alphabet: A finite non empty set of
elements.
∑∑ ={a,b,c,d,…z}

34. ∑
• String: A sequence of letters
– Examples: “cat”, “dog”, “house”, …
– Defined over an alphabet:
Σ={a, b, c,, z}
Language: It is a set of strings on some
alphabet

35. Alphabets and Strings
• We will use small alphabets:
• Strings Σ = { a, b}
a
u = ab
ab
v = bbbaaa
abba
w = abba
baba
aaabbbaabab

36. String Operations
abba
w = a1a2  an
bbbaaa
v = b1b2  bm
Concatenation
wv = a1a2  anb1b2 bm abbabbbaaa

37. w = a1a2  an ababaaabbb
Reverse
R
w = an  a2 a1 bbbaaababa

38. String Length
w = a1a2  an
w =n
• Length:
abba = 4
• Examples: aa = 2
a =1

39. Recursive Definition of Length
a =1
For any letter:
wa wa = w + 1
For any string : abba = abb + 1
= ab + 1 + 1
Example:
= a +1+1+1
= 1+1+1+1
=4

40. Length of Concatenation
uv = u + v
u = aab, u = 3
• Example: = abaab,
v v =5
uv = aababaab = 8
uv = u + v = 3 + 5 = 8

41. Proof of Concatenation Length
uv = u + v
• Claim:
v
• Proof: By induction on the length
v =1
– Induction basis:
– From definition of length:
uv = u +1 = u + v

42. uv = u + v
– Inductive hypothesis:
v = 1,2,, n
• for
– Inductive step: we will prove uv = u + v
–
– for v = n +1

43. Inductive Step
v = wa w = n, a = 1
• Write , where
uv = uwa = uw + 1
• From definition of length:
wa = w + 1
• From inductive hypothesis: uw = u + w
• Thus:
uv = u + w + 1 = u + wa = u + v

44. Empty String
λ
• A string with no letters:
λ =0
• Observations:
λw = wλ = w
λabba = abbaλ = abba

45. Substring
• Substring of string:
– a subsequence of consecutive
characters
abbab ab
• String Substring
abbab abba
abbab b
abbab bbab

46. Prefix and Suffix
• Prefixes Suffixes
abbab w = uv
λ abbab
a bbab prefix
ab bab suffix
abb ab
abba b
abbab λ

47. Another Operation
wn = ww w

 
n
( abba ) = abbaabba
2
• Example:
0
• Definition:
w =λ
–
( abba ) = λ
0

48. The * Operation
• Σ * : the set of all possible strings from
• Σ alphabet
Σ = { a, b}
Σ* = { λ, a, b, aa, ab, ba, bb, aaa, aab,}
•

49. The + Operation
+ : the set of all possible strings from
Σ
alphabet Σ except λ
Σ = { a, b}
Σ* = { λ , a, b, aa, ab, ba, bb, aaa, aab,}
+
Σ = Σ * −λ
+
Σ = { a, b, aa, ab, ba, bb, aaa, aab,}

50. Language
• A language is any subset of Σ*
Σ = { a, b}
• Example: Σ* = { λ , a, b, aa, ab, ba, bb, aaa,}
{ λ}
{ a, aa, aab}
• Languages:
{λ , abba, baba, aa, ab, aaaaaa}

51. Another Example
n n
L = {a b : n ≥ 0}
• An infinite language
λ
ab
∈L abb ∉ L
aabb
aaaaabbbbb

52. Operations on Languages
• The usual set operations
{ a, ab, aaaa}  { bb, ab} = {a, ab, bb, aaaa}
{ a, ab, aaaa}  { bb, ab} = {ab}
{ a, ab, aaaa} − { bb, ab} = { a, aaaa}
• Complement:
L = Σ * −L
{ a, ba} = { λ , b, aa, ab, bb, aaa,}

53. Reverse
R R
L = {w : w ∈ L}
• Definition:
•
{ ab, aab, baba} = { ba, baa, abab}
Examples:
R
n n
L = {a b : n ≥ 0}
R n n
L = {b a : n ≥ 0}

54. Concatenation
L1L2 = { xy : x ∈ L1, y ∈ L2 }
• Definition:
{ a, ab, ba}{ b, aa}
• Example:
= { ab, aaa, abb, abaa, bab, baaa}

55. Another Operation
Ln = 
LL  L
n
• Definition:
{ a, b}3 ={ a, b}{ a, b}{ a, b} =
{ aaa, aab, aba, abb, baa, bab, bba, bbb}
L0 = { λ}
• Special case:
0
{ a , bba , aaa } = { λ}

56. More Examples
n n
• L = {a b : n ≥ 0}
2 n n m m
L = {a b a b : n, m ≥ 0}
2
aabbaaabbb ∈ L

57. Star-Closure (Kleene *)
0 1 2
L* = L  L  L 
• Definition:
• Example: λ , 
a, bb, 
 
{ a, bb} * =  
 aa, abb, bba, bbbb, 
•
aaa, aabb, abba, abbbb,
 

58. Positive Closure
+ 1 2
L = L  L 
• Definition: = L * −{ λ }
a, bb, 
+  
{ a, bb} = aa, abb, bba, bbbb, 
aaa, aabb, abba, abbbb,
 

59. Finite Automaton
Input
•
String
Output
Finite String
Automaton