The document discusses various sampling techniques and methods for determining sample size in research, emphasizing the importance of representative samples. It categorizes sampling into probability and non-probability types, detailing specific techniques like simple random sampling, stratified sampling, and cluster sampling, alongside their advantages and disadvantages. The significance of accurately defining the population, selecting appropriate samples, and ensuring reliability in data collection processes is highlighted.

1. Sampling Techniques and Sample Size
Determination
By
Khem Raj Subedi
Associate Professor
TMC

2. Sampling Technique and Sample
Size Determination

3. Important statistical terms
Population:
a set which includes all
measurements of interest
to the researcher
(The collection of all responses,
measurements,
or counts that are of interest)
Sample:
A subset of the population

4. Population -hg;+Vof _
• 'Population refers to all the individuals
or objects on which we have to make
some study.'
cg';Gwfgsf] nflu 5gf]6 ul/Psf ;Dk"0f{ dflg;Pjd
j:t'x¿sf] ;d"xnfO{ ;du|jf hg;+VofelgG5.
• Finite Population l;ldt hg;+Vof
• Infinite Population cl;ldt hg;+Vof

5. Sample-gd'gf_
The representative proportion of the population is
called a sample. 7"nf] hg;+Vofaf6 5gf]6 ul/Psf] k|ltlglwd"ns
;d"xnfO{ g} gd"gf elgG5 .
Koul (2009: 111) sf cg';f/ æhg;ªVofsf] k|ltlglwd"nsc+znfO{ g}
gd'gf elgG5 .Æ (The respresentative portion of the
population is called sample).
Best & Khan (1998: 13) sf cg';f/ ægd'gfPp6f cjnf]sg /
ljZn]if0fsf nflu hg;ªVofaf6 5gf]6 ul/Psf] ;fgf] cg'kftxf] .Æ (A
sample is a small proportion of a population
selected for observation and analysis.)

6. Characteristics of a good sample
• A true representative of the population
• Free from error due to bias
• Adequate in size for being reliable
• Units of sample should be complete
precise and up to date
• free from random sampling error

7. Sampling gd"gf 5gf]6
• Sampling is the process of selecting a
representative part of a population for
the purpose of determining the
characteristics of the whole population.
• Gfd"gf 5gf]6 To:tf] k|lqmof xf] h;4f/f Jolqm, j:t' /
36gfx¿sf] ;fgf] ;+Vof 5gf]6 ul/G5 / ;Dk"0f{ hg;+Vofsf]
af/]dfslx s'/f kQfnufpgljZn]if0ful/G5.

8. Definitions of Sampling
• Kerlinger (1986:110) sf cg';f/ æhg;ªVof jf ;du|tfsf] k|ltlglwTj x'g] u/L
hg;ªVofsf] s]xL efu 5gf]6 ul/g] k|lj|mofnfO{ gd'gf 5gf]6 (sampling)
elgG5 . (sampling is process of selecting any portion of a
population or universe as representative of the
population or universe).
• Koul (2009: 111) sf cg';f/ ægd'gf 5gf]6 To:tf] k|lj|mof xf] h;åf/f JolQm,
j:t' / 36gfx¿sf] ;fk]lIft ¿kdf ;fgf] ;ªVof 5gf]6 ul/G5 / ;Dk"0f{ hg;ªVofsf af/]df
s]xLs'/fkQfnufO{ljZn]if0ful/G5 .Æ
• Sampling is the process by which a relatively small
number of individuals, objects or events is selected and
analyzed in order to find out something about the
entire population.

9. Why sampling?
• Get information about large populations
• Less costs
• Less field time
• More accuracy i.e. Can Do A Better Job of Data
Collection
• When it’s impossible to study the whole
population

10. Steps in sampling Method
• Defining the population
hg;+VofnfO{ kl/efliftug]{
• Listing the population (Sampling Frame)
hg;+Vofsf] ;"lr tof/ ug]{
• Selecting the representative sample
hg;+Vofsf] k|ltlgwLd"ns gd'gf 5g]6 ug]{
• Obtaining an adequate sample cfjZos
gd'gf k|fKtug]{

11. Sampling
Target
Population
Accessible
Population
Sample
FindingsGeneralization

12. Target Population:
The population to be studied/ to which the
investigator wants to generalize his results
Sampling Unit:
smallest unit from which sample can be
selected
Sampling frame
List of all the sampling units from which
sample is drawn
Sampling scheme
Method of selecting sampling units from
sampling frame

13. Sampling Techniques
& Samples Types

14. Types of sampling in researches
Probability
samples
;+efjgfo'Qm gd'gf
5gf}]6
Non-
probability
samples
;+efgf/lxt gd'gf
5gf}]6

15. Types of samples

16. ;+efjgfo"Qmgd'gf 5gf]6
(Probability Sampling)
• ;+efjgfo'Qm gd'gf 5gf]6nfO{ ;+of]u gd'gf 5gf]6 (chance
sampling) jf b}jLgd'gf5gf]6 (random sampling) klgelgG5 .
• o; ljlwdf cWoog hg;ªVofsf] k|To]s PsfOx¿ gd'gfsf ¿kdf 5gf]6 x'g ;Sg]
a/fa/ ;+efjgf x'G5 . To;}n] of] gd'gf 5gf]6 ljlw k"0f{ ¿kdf kIfkft /lxt
dflgG5 .
• cg';GwfgnfO{ a9L k|ltlglwd"ns Pjd kIfkft/lxt agfpgsf nflu ;Defjgfo'Qm
gd'gf5gf]6 k4ltsf]pkof]u ul/G5.

17. Simple Random Sample
• Every subset of a specified size n from the
population has an equal chance of being
selected

18. • Gay (1976: 68) sf cg';f/ æ;fdfGo ;+efjgfo'Qm gd'gf 5gf]6 cg';Gwfgsf] nflu
gd'gf 5gf]6 ug{] To:tf] ljlw xf] h;df kl/eflift ul/Psf] hg;ªVofdf /x]sf ;a} JolQmx¿
gd'gfsf] ¿kdf 5gf]6 x'g] ;Defjgf ;dfg / :jtGq
x'G5Æ .
• d'Vou/L lgDg ljlwx¿dWo] s'g} Psljlwsf] k|of]u ug{ ;lsG5 .
• uf]nf k|yf ljlw(Lottery method)
• ufO{ lqz'n (Coin-toss method)
• sf8{ ljlw(Card method)
• b}ljs c+ssf] tflnsfsf] k|of]u (Table of random number)
• Kjfn ljlw(Grid method)
• sDKo'6/ ljlw(Computer method)
• b}ljs c+s 8fon (Random digit dialing-RDD)

19. Advantages
1.Easy to conduct
2.High probability of achieving a representative
sample
3. Meets assumptions of many statistical
procedures
Disadvantages
1.Identification of all members of the population
can be difficult
2. Contacting all members of the sample can be
difficult

20. Systematic Sample
• Every kth member ( for example: every 10th
person) is selected from a list of all population
members.

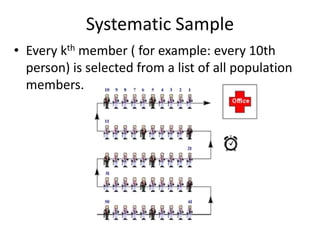
21. Jojl:ytgd'gf 5gf]6 ljlw
(Systematic sampling)
• Jojl:yt gd'gf 5gf]6 To:tf] ljlw xf], h;df ;+efJotfsf cfwf/df ;du|
hg;ªVofaf6 Pp6f PsfO -gd'gf_ sf] 5gf]6 u/L lglZrt gd'gf cGt/
(sample interval) sf cfwf/df cGo afFsL gd'gfsf] 5gf]6
ul/G5 . o;nfO{cw{ ;+efjgfo'Qmgd'gf 5gf]6 klgelgG5 .
gd'gf 5gf]6 cGt /fn (Sampling Interval) =
(Sizeof population)
(Sizeof samplerequired)
hg; V+ofsf]cfsf/
r flxg]gd'gfsf]cfsf/
K = N
n

22. Advantage
•Very easily done
Disadvantages
•Some members of the population don’t
have an equal chance of being included

23. Stratified Random Sample
• The population is divided into two or more groups
called strata, according to some criterion, such as
geographic location, grade level, age, or income, and
subsamples are randomly selected from each strata.

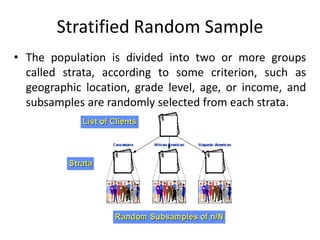
24. :tLl/s[t gd'gf 5gf]6
(stratified sampling):
• ;du|tf jf cWoog hg;+Vof leq /x]sf ljleGg PsfOx?sf] ljz]iftfsf cfwf/df
PsfOx?nfO{ :t/Ls[t u/L ;+efjgfo'Qm gd'gf 5gf]6 (random sampling)
ljwLaf6 gd'gf 5gf]6 ug]{ k|lqmof jf tl/sfnfO{ :t/Ls[t gd'gf 5gf]6 (Stratified
sampling) elgG5.
• obL cWoog hg;+Vofsf] :j?k jf jgfj6 c;dfg (heterogeneous) 5 eg] To;
cj:yfdf:t/Ls[tgd'gf5gf]6ljwLj9Lpko'Qmx'G5 .
• :t/Ls[t gd'gf 5gf]6 ljlw k|of]u ubf{ cg';Gwfgsf] p2]Zo cg';f/ cWoog
hg;ªVofnfO{ ln·, pd]/, z}lIfs cj:yf, k];f, wd{, hftL, a;f]af; If]q -zx/÷ufpF_,
;fdflhs cfly{s cj:yf, ef}uf]lns If]q h:tf ljz]iftfx¿sf cfwf/df ljleGg ju{ (Strata)
df ljefhg ul/G5 / k|To]s ju{af6 ;Defjgfo'Qm gd'gf 5gf]6 ljlwsf] k|of]u u/L
gd'gf5gf]6ul/G5 .

25. Advantages
•More accurate sample
•Can be used for both proportional and non-
proportional samples
•Representation of subgroups in the sample
Disadvantages
•Identification of all members of the population can
be difficult
•Identifying members of all subgroups can be
difficult

26. Cluster Sample
• The population is divided into subgroups
(clusters) like families. A simple random sample
is taken of the subgroups and then all members
of the cluster selected are surveyed.

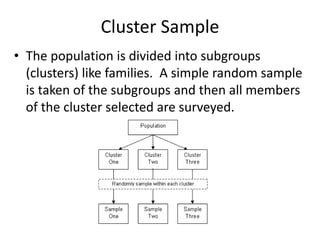
27. em'08 gd'gf 5gf]6
(Cluster Sampling)
• of] ljlw cl;ldt hg;ªVof (infinite population) ePdf, hg;ªVofsf]
;"rL k|fKt x'g g;Sbf jf hg;ªVof 5l/P/ (scatter) /x]sf] cj:yfdf tyf
hg;ªVofsf] ef}uf]lns ljt/0f 7"nf] ePsf] cj:yfdf a9L pko'Qm x'G5
(Best and Khan, 1999:18) . ;du| hg;ªVof jf If]qnfO{ ljleGg
e'm08df ljefhg u/L gd'gf 5gf]6 ug{] ljlwnfO{ em"08 gd'gf 5gf]6
(Cluster sampling) elgG5 .

28. Cluster sampling
Section 4
Section 5
Section 3
Section 2
Section 1

29. Advantages
•Very useful when populations are large and
spread over a large geographic region
•Convenient and expedient
•Do not need the names of everyone in the
population
Disadvantages
•Representation is likely to become an issue

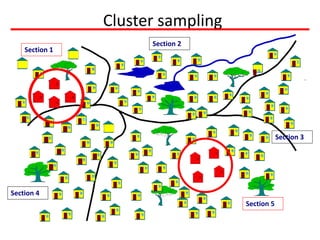
30. ax'r/0f gd'gf 5gf]6 (Multistage Sampling)
• ;du| hg;ªVofnfO{ ljleGg txdf Pskl5 csf{] ljefhg ub{} tNnf] txdf
k'u]/ gd'gf 5gf]6 ug{] ljlwnfO{ ax'tx gd'gf 5gf]6 (Multistage
sampling) elgG5 . o; gd'gf 5gf]6 ljlw cg';f/ cg';Gwfgsf nflu
gd'gf 5gf]6 ubf{ ljleGg r/0fx¿df ljefhg u/L ax'txaf6 clt z'Id PsfOdf
k'u]/gd'gf 5gf]6 ul/G5 .

31. Non-Probability Sampling

32. Non-Probability Sampling
• s'g} hg;ªVofaf6cWoogsf nflu5gf]6 ul/g]gd'gf;+of]usf]
cfwf/df geO{ k"j{lgwf{l/t;f]r jf ljrf/sf cfwf/df ul/G5, h;df k|To]s
PsfOx¿ gd'gfsf¿kdf 5gf]6 x'g] ;+efjgfx'Fb}geg] To;nfO{;+efjgf
/lxtgd'gf 5gf]6 (Non-Probability Sampling) elgG5 .
• Pant (2012) sf cg';f/ "Non-Probability sampling
is described as those samples, which are not
determined by chances but rather by personal
convenience or judgment of the researcher."

33. ;+efjgf/lxtgd'gf5gf]6 ljlwsf]k|of]ux'g]cj:yfx¿
• ha hg;ªVofsfPsfOx¿sf];ªVofyfxfgePsf]cj:yfdfjfJolQmut¿kdfklxrfg
gePsf]cj:yfdf.
• cg';Gwfgstf{n];+efjgfo'Qmgd'gf5gf]6ubf{hg;ªVofsfaf/]dfk"0f{hfgsf/L
k|fKtgePsf]n]cj:yfdf.
• cg';Gwfgstf{n]cWoogsf36gfx¿sf]7"nf];ªVof;dfj]zug{ c;+ej÷cJojxfl/sdx;';
u/]sfn] cj:yfdf.
• olbcg';Gwfgu'0ffTdsk|s[ltsf]Pj+36gfcWoogePdf.
• ;+efjgfo'Qmgd'gf5gf]6ljlwdfkm{t5gf]6ul/Psfgd'gfnfO{;Dks{ug{sl7gfO
k|dfl0ftePdf.h:t}M3/ljlxg(homeless) jfnfu'cf}ifw;]jgstf{ (Drug
addicts), dlxnfof}gsdL{x? (Female sex workers) cflbJolQmsf]
cWoog.

34. Convenience Sample
• Selection of whichever individuals are easiest to reach
• the process of including whoever happens to be
available at the time
• …called “accidental” or “haphazard” sampling
• It is done at the “convenience” of the researcher

35. disadvantages…
…difficulty in determining how much
of the effect (dependent variable)
results from the cause (independent
variable)

36. Purposive Sample
the process whereby the researcher selects a
sample based on experience or knowledge
of the group to be sampled
…called “judgment” sampling

37. p2]Zod"ns gd'gf 5gf]6
(Purposive sampling)
• p2]Zod"ns gd'gf 5gf]6df cg';Gwfgstf{sf] p2]Zo, ?rL / rfxgf cg';f/ gd'gfsf]
5gf]6 ul/G5 . cg';Gwfgstf{n] h'g p2]Zo cGtu{t /x]/ cg';Gwfg sfo{ ug{ nfu]sf]
xf] ;f]xL p2]Zo adf]lhd cfˆgf] JolQmut lg0f{osf cfwf/df gd'gf 5gf]6 u5{ eg]
To:tf] gd'gf 5gf]6 ljlwnfO{ p2]Zod"ns gd'gf 5gf]6 ljlw (purposive
sampling) elgG5.
• o; ljlwdf cg';Gwfgstf{n] gd'gf 5gf]6 ubf{ cfˆgf] ljifout cfwf/ (Subjective
basis), p2]Zo (objective) Pj+ cGtb{[li6 (intuition) k|of]u u/L
cfkm} lg0f{o ug{] ePsf]n] o;nfO{ lg0f{ofTds gd'gf 5gf]6 (Judgemental
sampling) klgelgG5.

38. disadvantages…
…potential for inaccuracy in the researcher’s
criteria and resulting sample selections

39. Quota Sample
1. Determine what the population looks like
in terms of specific qualities.
2. Create “quotas” based on those qualities.
3. Select people for each quota.

40. Quota sampling
• cg';Gwfgstf{n]hg;ªVofnfO{lglZrtljz]iftfsfcfwf/dfljleGg
PsfOx¿nfO{cf/If0fsf¿kdfljleGg;d"x(strata)dfljefhgu/L
cg';Gwfgstf{sf]JolQmut lg0f{osfcfwf/dfk|To]s ;d"xsf];dfg'kflts
k|ltlglwTjx'g]u/Lgd'gf5gf]6ug{]ljlwnfO{cf/If0fgd'gf5gf]6
(Quota sampling) elgG5.
• cWooghg;ªVofnfO{slt;d"xdfljefhgug]{xf], ;f]lg0f{oug{]
• k|To]s ;d"xaf6gd'gfsf]sltk|ltztlng'kg{]xf],;f]s'/flg0f{oug{]
• jf:tljsgd'gfPsfOx¿sf]5gf]6ug{]

41. disadvantages…
…people who are less accessible (more
difficult to contact, more reluctant to
participate) are under-represented

42. Snowball Sample
 In this method the first members of the sample
are identified.
 Subsequent members of the sample come by
recommendation or identification by the first
members.
 This does not guarantee a representative sample,
but it can be the best method when the subject of
research is sensitive or relates to a population that is
hard to contact (e.g people engaged in social security
fraud).

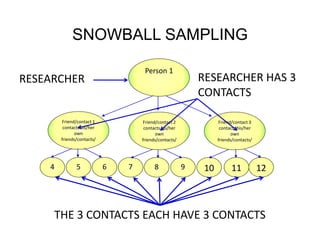
43. Snowball sampling
• :gf]an gd'gf 5gf]6 ljlwaf6 gd'gf 5gf]6 ubf{ ;j{k|yd cWoog
hg;ªVofsf] s'g} Pp6f PsfOnfO{ gd'gfsf] ¿kdf lnO{ To; PsfOsf]
dfWodaf6 cGo PsfOx¿nfO{ kQf nufpFb} gd'gf 5gf]6 ul/G5 . o;
ljlwdf s'g} Ps PsfOsf] klxrfg kl5 5gf]6 ul/Psf] pQm gd'gfn]
lbPsf] ;"rgf jf hfgsf/Lsf cfwf/df csf{] gd'gf 5gf]6 ul/G5 o;/L Ps
kl5 csf{] ub{} k|fKt ;"rgfsf] cfwf/df ;+hfn (network)
k|lj|mofaf6 cfjZos ;ªVofdf gd'gf 5gf]6 ug{] ljlwnfO{ :gf]jn gd'gf
5gf]6 (Snowball sampling) elgG5 .

44. Person 1
Friend/contact 1
contacts his/her
own
friends/contacts/
Friend/contact 2
contacts his/her
own
friends/contacts/
Friend/contact 3
contacts his/her
own
friends/contacts/
4 5 6 7 8 9 10 11 12
RESEARCHER RESEARCHER HAS 3
CONTACTS
THE 3 CONTACTS EACH HAVE 3 CONTACTS
SNOWBALL SAMPLING

45. The Theoretical Sample

46. 46
Ways to Determine Sample Size
• Blind guess
• Available budget
• Bayesian considerations
• Rules of thumb
– Main group n > 100
– Subgroups 20 < n < 100
• Standards for comparable studies
• Statistical precision

47. 47
Statistical Precision
Must know:
• Variability of population and individual
stratum
• Acceptable level of sampling error
• Needed level of confidence
• Type of distribution (if non-normal)

48. 48
Sample Size Formula
2






E
zs
n
where:
n = sample size
z = confidence interval in standard error units
s = standard error of the mean
E = acceptable magnitude of error

49. 49
Sample Size Formula:
Example #1
Suppose a survey researcher, studying
expenditures on lipstick, wishes to have a 95%
confident level (Z) and a range of error (E) of
less than $2.00. The estimate of the standard
deviation is $29.00.

50. 50
2
E
zs
n 






   2
00.2
00.2996.1





2
00.2
84.56




  2
42.28 808
Calculation: Example #1

51. 51
Suppose, in the same example as the one
before, the range of error (E) is acceptable at
$4.00. By how much is sample size is
reduced?
Sample Size Formula:
Example #2

52. 52
2
E
zs
n 






   2
00.4
00.2996.1





2
00.4
84.56






  2
21.14 202
Calculation: Example #2

53. 53
2
2
E
pqZ
n 
Cochran (1977) developed a formula to calculate a
representative sample for
proportions as

54. 54
2
2
E
pqz
n 
Where:
n = number of items in samples
Z2 = square of confidence interval in standard error units
p = estimated proportion of success
q = (1-p) or estimated the proportion of failures
E2 = square of maximum allowance for error between true
proportion and sample proportion, or zsp squared.

55. 55
Ex 1 Calculating Sample Size
at the 95% Confidence Level
753
001225.
922.

001225
)24)(.8416.3(

)035( .
)4)(.6(.)961.(
n
4.q
6.p
2
2


