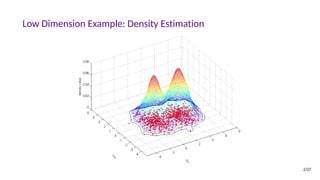
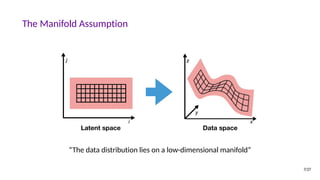
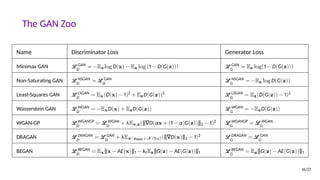
Generative adversarial networks (GANs) are a class of machine learning frameworks where two neural networks compete against each other. One network generates new data instances, while the other evaluates them for authenticity. This adversarial process allows the generating network to produce highly realistic samples matching the training data distribution. The document discusses the GAN framework, various algorithm variants like WGAN and BEGAN, training tricks, applications to image generation and translation tasks, and reasons why GANs are a promising area of research.

1. Introduction to Generative Adversarial Networks
Oct 16, 2018
Jong Wook Kim
Music and Audio Research Laboratory, New York University

2. Generative Modeling
data
→
probability distribution
{x1, x2, · · · , xN} p(x)
1/27

3. Generative Modeling
data
→
probability distribution
{x1, x2, · · · , xN} p(x)
vs. Discriminative Models:
labeled data
→
conditional probability distribution
{(x1, y1), (x2, y2), · · · , (xN, yN)} p(y | x)
1/27

4. Low Dimension Example: Density Estimation
2/27

5. High Dimension Example: Sample Generation
→
data samples
[Berthelot et al. 2017, BEGAN]
3/27

6. Why Study Generative Models?
• Test of our ability to use high-dimensional, complicated probability distributions
• Simulate possible futures for planning or reinforcement learning
• Missing data, semi-supervised learning
• Multi-modal outputs
• Realistic generation tasks
[Goodfellow, NIPS 2016 Tutorial]
4/27

7. The 2-D case
Assume a Gaussian Mixture Model:
• p(x|π, μ, ) = i πi (μi, i)
5/27

8. The 2-D case
Assume a Gaussian Mixture Model:
• p(x|π, μ, ) = i πi (μi, i)
Perform maximum likelihood estimation:
• maxπ,μ, x(j)∈data log p(x(j)|π, μ, )
5/27

9. The 2-D case
• Density estimation:
• Sample generation:
Go-to generative model for low-dimensional data
6/27

10. The Manifold Assumption
Latent space Data space
“The data distribution lies on a low-dimensional manifold”
7/27

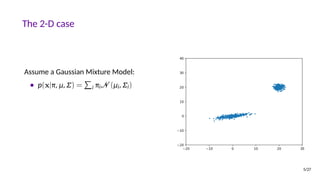
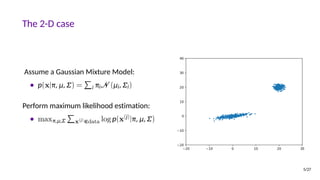
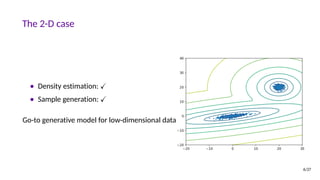
11. Latent Space Interpolation
[Berthelot et al. 2017, BEGAN]
8/27

12. Latent Space Arithmetic
[Radford et al. 2015, DCGAN]
9/27

13. Building Manifold using a Decoder
10/27

14. Building Manifold using a Decoder
Question: how should we measure if the generation is good?
10/27

15. Autoencoder: Make it Reconstruct the Original Image
• Vanilla AE
– Still needs a generative model (like GMM) on the latent space
• Variational Autoencoders (VAE)
– Variational approximation results in a blurry image.
11/27

16. btw: L2 Distance doesn’t Work Very Well for Image Similarity
12/27

17. Idea: Use a Neural Network to Evaluate Generation
13/27

18. Idea: Use a Neural Network to Evaluate Generation
Question: how does the discriminator know about the data distribution? 13/27

19. The GAN Architecture
14/27

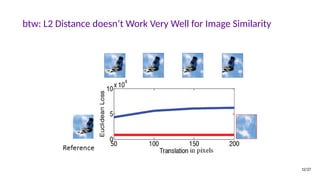
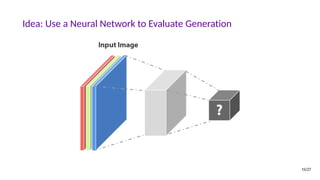
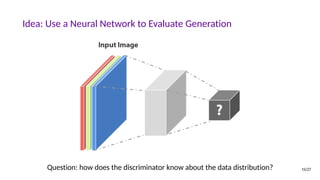
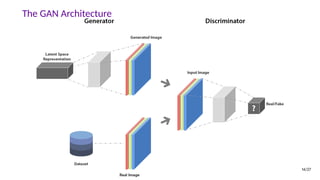
20. The GAN Formula
min
G
max
D
[︁
Ex∼pdata log D(x) + Ez∼pz log (1 − D(G(z)))
]︁
(1)
• A minimax game between the generator and the discriminator.
• In practice, a non-saturating variant is often used for updating G:
max
G
Ez∼pz log D(G(z)) (2)
[Goodfellow et al. 2014, Generative Adversarial Nets]
15/27

21. The GAN Zoo
Name Discriminator Loss Generator Loss
Minimax GAN GAN
D
= −Exlog D(x) − Ez log (1 − D(G(z))) GAN
G
= Ez log(1 − D(G(z)))
Non-Saturating GAN NSGAN
D
= GAN
D
NSGAN
G
= −Ez log D(G(z))
Least-Squares GAN LSGAN
D
= Ex(D(x) − 1)2 + EzD(G(z))2 LSGAN
G
= Ez(D(G(z)) − 1)2
Wasserstein GAN WGAN
D
= −ExD(x) + EzD(G(z)) WGAN
G
= −EzD(G(z))
WGAN-GP WGANGP
D
= WGAN
D
+ λEx,z( ∇D(αx + (1 − α)G(z)) 2 − 1)2 WGANGP
G
= WGAN
G
DRAGAN DRAGAN
D
= GAN
D
+ λEx∼pdata+ (0,c)( ∇D(x) 2 − 1)2 DRAGAN
G
= GAN
G
BEGAN BEGAN
D
= Ex x − AE(x) 1 − ktEz G(z) − AE(G(z)) 1
BEGAN
G
= Ez G(z) − AE(G(z)) 1
16/27

22. Wasserstein GAN and the Earth-Mover Distance
EMD(Pdata, Pz) = inf
γ∼(Pdata,Pz)
E(x,y)∼γ x − y (3)
• First introduced by Arjovsky et al. using weight clipping
• An algorithm using a gradient penalty (WGAN-GP) is now the standard
• Member of a broader family of IPMIntegral Probability Metrics-based GANs 17/27

23. Training Tricks
• Improved Techniques for Training GANsTalimans et al. 2016
– Feature matching
– One-sided label smoothing
• GAN Hacks https://github.com/soumith/ganhacks
– Use BatchNorm, but do not mix real and fake batches
– Avoid sparse gradients by using LeakyReLU
• Two Time-scale Update RuleHeusel et al. 2017
– Train the discriminator faster than generator
• Progressive Growing of GANsKarras et al. 2017
– Start with low resolution and linearly interpolate to higher dimensions
18/27

24. Conditional Generation
(noise)(latent)
(data)
InfoGAN
(Chen, et al., 2016)
. . .
(noise)(class)
(data)
AC-GAN
(Odena, et al., 2016)
(noise)(class)
(data)
Conditional GAN
(Mirza & Osindero, 2014)
(noise)
. . .
(class)
(data)
Semi-Supervised GAN
(Odena, 2016; Salimans, et al., 2016)
19/27

25. Projection Discriminator
[Miyato & Koyama, 2018] 20/27

26. GANs with Encoder
features data
z G G(z)
xEE (x)
G(z), z
x, E (x)
D P (y)
[Donahue et al., 2017, Dumoulin et al., 2017]
21/27

27. Superresolution
bicubic SRResNet SRGAN original
(21.59dB/0.6423) (23.53dB/0.7832) (21.15dB/0.6868)
[Ledig et al., 2016]
22/27

28. Image-to-Image Translation
[Zhu et al., 2016] 23/27

29. WaveGAN and Speech Enhancement GAN
Phase shuffle n=1
-1 0 +1
[Donahue et al. 2018, Pascual et al. 2017]
24/27

30. Reasons to Love GANs
• GANs set up an arms race
• GANs can be used as a “learned loss function”
• GANs are “meta-supervisors”
• GANs are great data memorizers
• GANs are democratizing computer art
[Alexei A. Efros, CVPR 2018 Tutorial]
25/27

31. MSE and MAE do not Account for Multi-Modality
[Sønderby et al., 2017]
26/27

32. Programming GANs
• Needs to fix the opponent’s weights during each update
• Framework-dependent:
– Keras: hack with the trainable flag
– TensorFlow: tf.contrib.gan contains off-the-shelf algorithms
– PyTorch: Call appropriate backward() for each update
• There are tons of examples, and the best way to learn is to read them
27/27