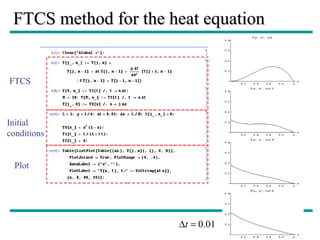
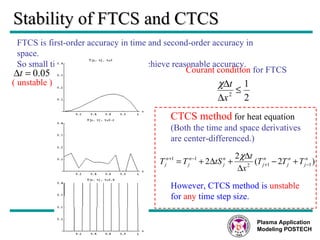
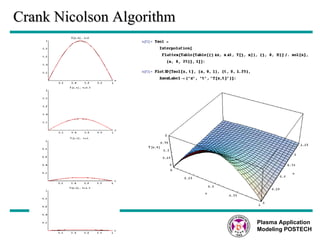
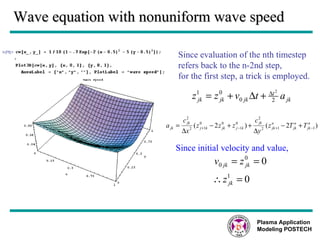
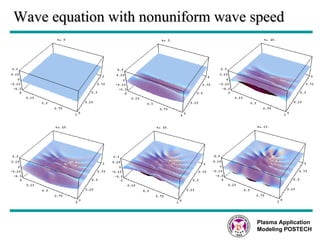
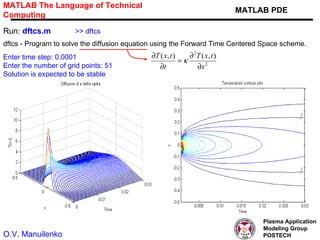
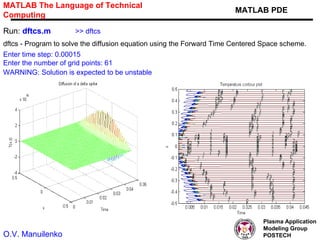
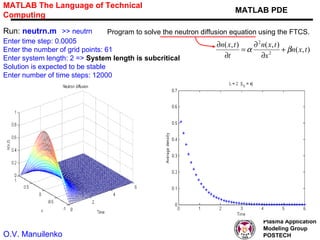
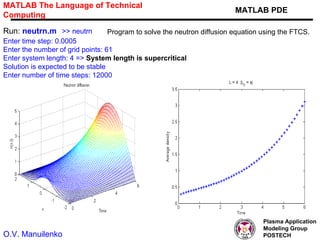
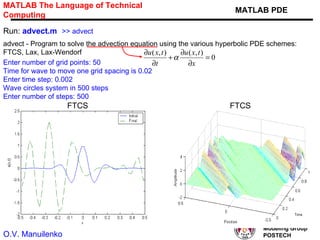
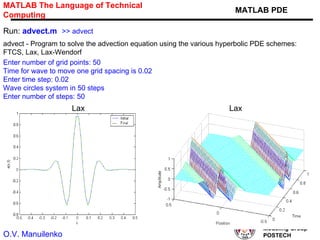
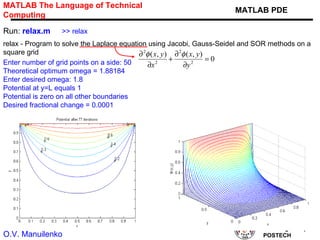
This document discusses several numerical methods for solving partial differential equations (PDEs) using Mathematica and MATLAB. It covers finite difference methods like FTCS, Lax, Crank-Nicolson for parabolic PDEs. It also discusses Jacobi's method, SOR method for elliptic PDEs and finite difference schemes for hyperbolic PDEs. MATLAB code examples are provided to implement these methods for different PDEs like heat equation, wave equation and Poisson's equation.