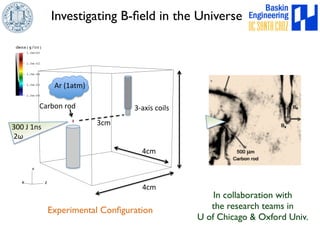
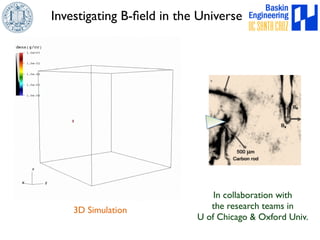
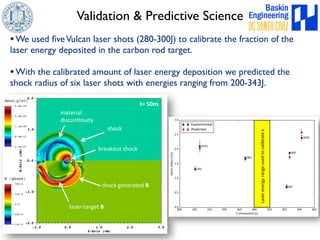
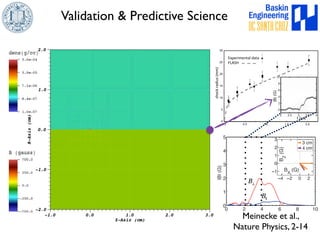
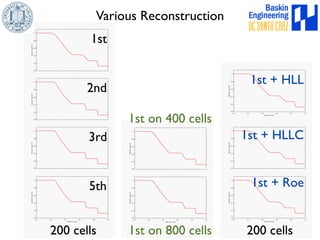
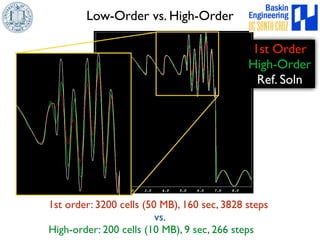
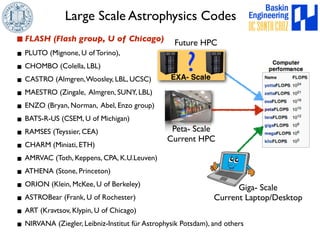
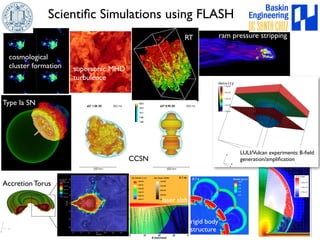
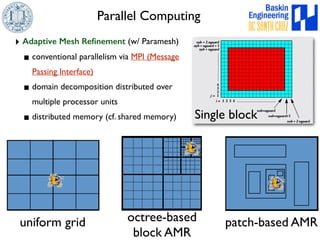
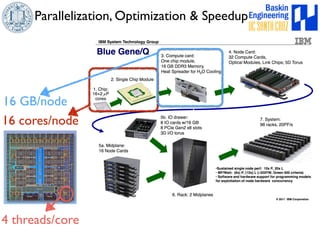
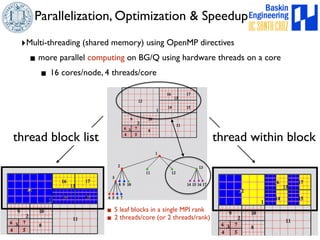
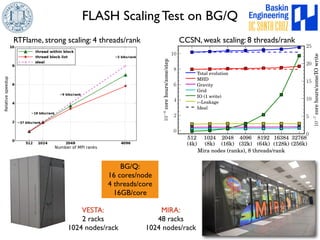
This document discusses high-order numerical methods for predictive science on large-scale high-performance computing architectures. It covers three main topics: 1) High performance computing and how modern architectures have increasing numbers of cores but declining memory per core, requiring a shift in numerical algorithms. 2) Ideas on high-order numerical methods that are more accurate using less grid points and higher-order approximations. 3) The importance of validating and verifying simulations against theoretical solutions and experiments for predictive science.

1. High-order Numerical
Methods for Predictive Science on
Large-scale High-performance
Computing Architectures
Dongwook Lee
Applied Mathematics & Statistics
University of California, Santa Cruz
Mathematics Colloquium, November 18, 2014
FLASH Simulation of a 3D Core-collapse Supernova
Courtesy of S. Couch
MIRA, BG/Q, Argonne National Lab
49,152 nodes, 786,432 cores OMEGA Laser (US)

2. Cyclic Relationship
Theory
Experiment Scientific
Computation
validation
verification

3. Example: Supersonic Airflow
Theory
Experiment Simulation

4. Topics for Today
1. High Performance Computing
2. Ideas on Numerical Methods
3. Validation & Predictive Science

5. First Episode
1. High Performance Computing
2. Ideas on Numerical Methods
3. Validation & Predictive Science

6. High Performance Computing (HPC)
‣To solve large problems in science, engineering, or
business
‣Modern HPC architectures have
▪ increasing number of cores
▪ declining memory/core
‣This trend will continue for the foreseeable future

7. High Performance Computing (HPC)
‣This tension between computation & memory brings a
paradigm shift in numerical algorithms for HPC
‣To enable scientific computing on HPC architectures:
▪ efficient parallel computing, (e.g., data parallelism, task
parallelism, MPI, multi-threading, GPU accelerator, etc.)
▪ better numerical algorithms for HPC

8. Numerical Algorithms for HPC
‣Numerical algorithms should conform to the
abundance of computing power and the scarcity of
memory.
‣But…
▪ without losing solution accuracy.
▪ with maintaining maximum solution stability.
▪ with faster convergence to a “correct” solution.

9. High-Order Numerical Algorithms
‣ A good solution to this is to use high-order algorithms.
‣ They provide more accurate numerical solutions using
▪ less grid points (=memory save).
▪ higher-order mathematical approximations (promoting
more floating point operations, or computation).
▪ faster convergence to solution.

10. Large Scale Astrophysics Codes
▪FLASH (Flash group, U of Chicago)
Future HPC
▪ PLUTO (Mignone, U of Torino),
▪ CHOMBO (Colella, LBL)
▪ CASTRO (Almgren, Woosley, LBL, UCSC)
▪ MAESTRO (Zingale, Almgren, SUNY, LBL)
▪ ENZO (Bryan, Norman, Abel, Enzo group)
▪ BATS-R-US (CSEM, U of Michigan)
▪ RAMSES (Teyssier, CEA)
Peta- Scale
▪ Current HPC
CHARM (Miniati, ETH)
▪ AMRVAC (Toth, Keppens, CPA, K.U.Leuven)
▪ ATHENA (Stone, Princeton)
▪ ORION (Klein, McKee, U of Berkeley)
▪ ASTROBear (Frank, U of Rochester)
▪ ART (Kravtsov, Klypin, U of Chicago)
▪ NIRVANA (Ziegler, Leibniz-Institut für Astrophysik Potsdam), and others
Giga- Scale
Current Laptop/Desktop
?

11. The FLASH Code
‣FLASH is is free, open source code for astrophysics and HEDP.
▪ modular, multi-physics, adaptive mesh refinement (AMR), parallel
(MPI & OpenMP), finite-volume Eulerian compressible code for
solving hydrodynamics and MHD
▪ professionally software engineered and maintained (daily
regression test suite, code verification/validation), inline/online
documentation
▪ 8500 downloads, 1500 authors, 1000 papers
▪ FLASH can run on various platforms from laptops to
supercomputing (peta-scale) systems such as IBM BG/P and BG/Q.

12. Scientific Simulations using FLASH
cosmological
cluster formation supersonic MHD
turbulence
Type Ia SN
RT
CCSN
ram pressure stripping
laser slab
rigid body
structure
Accretion Torus
LULI/Vulcan experiments: B-field
generation/amplification

13. Parallel Computing
‣ Adaptive Mesh Refinement (w/ Paramesh)
▪conventional parallelism via MPI (Message
Passing Interface)
▪domain decomposition distributed over
multiple processor units
▪distributed memory (cf. shared memory)
Single block
uniform grid octree-based
block AMR
patch-based AMR

14. Parallelization, Optimization & Speedup
16 GB/node
16 cores/node
4 threads/core

15. Parallelization, Optimization & Speedup
‣Multi-threading (shared memory) using OpenMP directives
▪more parallel computing on BG/Q using hardware threads on a core
▪ 16 cores/node, 4 threads/core
thread block list thread within block
▪ 5 leaf blocks in a single MPI rank
▪ 2 threads/core (or 2 threads/rank)

16. FLASH Scaling Test on BG/Q
RTFlame, strong scaling: 4 threads/rank CCSN, weak scaling: 8 threads/rank
VESTA:
2 racks
1024 nodes/rack
10
8
6
4
2
MIRA:
48 racks
1024 nodes/rack
BG/Q:
16 cores/node
4 threads/core
16GB/core
512
(4k)
1024
(8k)
2048
(16k)
4096
(32k)
8192
(64k)
16384
(128k)
25
20
15
10
5
32768
(256k)
Mira nodes (ranks), 8 threads/rank
0
108 core hours/zone/step
0
107 core hours/zone/IO write
Total evolution
MHD
Gravity
Grid
IO (1 write)
⌫-Leakage
Ideal

17. Second Episode
1. High Performance Computing
2. Ideas on Numerical Methods
3. Validation Predictive Science

18. Scientific Tasks
Science Problem
(IC, BC, ODE/PDE)
Simulator
(code, computer)
Results
(Validation, verification,
analysis)

19. 1. Mathematical Models
Hydrodynamics (gas dynamics)
@⇢
@t
+ r · (⇢v) = 0 mass eqn
@⇢v
@t
+ r · (⇢vv) + rP = ⇢g momentum eqn
@⇢E
@t
+ r · [(⇢E + P)v] = ⇢v · g total energy eqn
P = (! 1)⇢✏
E = ✏ +
1
2|v|2
@⇢✏
@t
+ r · [(⇢✏ + P)v] − v · rP = 0
Equation of State

20. 2. Mathematical Models
Magnetohydrodynamics (MHD)
@⇢
@t
+ r · (⇢v) = 0 mass eqn
@⇢v
@t
+ r · (⇢vv − BB) + rP⇤ = ⇢g + r · ⌧ momentum eqn
@⇢E
@t
+ r · [v(⇢E + P⇤) − B(v · B)] = ⇢g · v + r · (v · ⌧ + $rT) + r · (B ⇥ (⌘r⇥B))
total energy eqn
@B
@t
+ r · (vB − Bv) = −r ⇥ (⌘r⇥B) induction eqn
P⇤ = p +
B2
2
E =
v2
2
+ ✏ +
B2
2⇢
Equation of State
⌧ = μ[(rv) + (rv)T −
2
3
solenodidal constraint
(r · v)I]
viscosityr · B = 0

21. 3. Mathematical Models
HEDP: Separate energy eqns for ion, electron, radiation
(“3-temperature, or 3T”)
@
@t
(⇢✏ion) + r · (⇢✏ionv) + Pionr · v = ⇢
cv,ele
⌧ei
(Tele − Tion) ion energy
@
@t
(⇢✏ele) + r · (⇢✏elev) + Peler · v = ⇢
cv,ele
⌧ei
(Tion − Tele)−r· qele + Qabs − Qemis + Qlas electron energy
@
@t
(⇢✏rad) + r · (⇢✏radv) + Pradr · v = r · qrad − Qabs + Qemis radiation energy
✏tot = ✏ion + ✏ele + ✏rad
Ptot, Tion, Tele, Trad = EoS(⇢, ✏ion, ✏ele, ✏rad) 3T EoS
Compare 3T with a simple 1T EoS!
@
@t
(⇢✏tot) + r · (⇢✏totv) + Ptotr · v = 0
Ptot = EoS(⇢, ✏tot)
Tion = Tele = Trad, or Tele = Tion, Trad = 0

22. Discretization Approaches
‣Finite Volume (FV)
▪shock capturing, compressible flows, structured/unstructured grids
▪hard to achieve high-order (higher than 2nd order)
‣Finite Difference (FD)
▪smooth flows, incompressible, high-order methods
▪non-conservative, simple geometry
‣Finite Element (FE)
▪arbitrary geometry, basis functions, continuous solutions
▪hard coding, problems at strong gradients
‣Spectral Element (SE)
‣Discontinuous Galerkin (DG)

23. Finite Volume Formulations
@U
@t
+
@F
@x
+
@G
@y
+
@H
@z
= 0
@U
@t
+ r · Flux(U) = 0
‣ Conservation laws (mass, momentum, energy)
‣ Highly compressible flows with shocks and discontinuities
‣ Differential (smooth) form of PDEs (e.g., FD) becomes invalid
‣ Integral form of PDEs relaxes the smoothness assumptions and seek
for weak solutions over control volumes and boundaries
‣ Basics of FV (in 1D):
U i+1 n
x
t
Un+1
i
Un
i Un
i1
tn+1
tn
Fn
i1/2 Fn
i+1/2
or

24. Finite Volume Formulations
‣ Integral form of PDE:
Z xi+1/2
xi1/2
u(x, tn+1)dx
Z xi+1/2
xi1/2
u(x, tn)dx =
Z tn+1
tn
f(u(xi1/2, t))dt
Z tn+1
tn
f(u(xi+1/2, t))dt
‣ Volume averaged, cell-centered quantity time averaged flux:
Un
i =
1
x
Z xi+1/2
xi1/2
and f(u(xi1/2, t))dt
u(x, tn)dx Fn
i1/2 =
‣ Finite wave speed in hyperbolic system:
1
t
Z tn+1
tn
Fn
i1/2 = F(Un
i ) * High-order reconstruction in space time
i1, Un
* Riemann problem at each cell-interface, i-1/2
‣ General discrete difference equation in conservation form in 1D:
Un+1
i = Un
i
t
x
(Fn
i+1/2 Fn
i1/2)

25. Riemann Problem Godunov Method
‣The Riemann problem:
‣Two cases:
PDEs: Ut + AUx = 0,−1 x 1, t 0
IC : U(x, t = 0) = U0(x) =
(
UL if x 0,
UR if x 0.
Shock
solution
Rarefaction
solution

26. A Discrete World of FV
U(x, tn)
xi1 xi xi+1

27. A Discrete World of FV
piecewise polynomial reconstruction
on each cell
u(xi, tn) = Pi(x), x 2 (xi1/2, xi1/2)
xi1 xi xi+1
uR = Pi(xi+1/2) uL = Pi+1(xi+1/2)

28. A Discrete World of FV
At each interface we solve a RP and obtain Fi+1/2
xi1 xi xi+1

29. A Discrete World of FV
We are ready to advance our solution in time and
get new volume-averaged states
Un+1
i = Un
i
t
x
⇣
F⇤ i+1/2 F⇤ i−1/2
⌘

30. High-Order Polynomial Reconstruction
PLM PPM
FOG
• Godunov’s order-barrier theorem (1959)
• Monotonicity-preserving advection schemes are at most first-order! (Oh no…)
• Only true for linear PDE theory (YES!)
• High-order “polynomial” schemes became available using non-linear slope limiters
(70’s and 80’s: Boris, van Leer, Zalesak, Colella, Harten, Shu, Engquist, etc)
• Can’t avoid oscillations completely (non-TVD)
• Instability grows (numerical INSTABILITY!)

31. Low vs. High order Reconstructions

32. Traditional High-Order Schemes
‣ Traditional approaches to get Nth high-order schemes take (N-1)th
degree polynomial for interpolation/reconstruction
▪only for normal direction (e.g., PLM, PPM, ENO, WENO, etc)
▪with monotonicity controls (e.g., slope limiters, artificial viscosity)
‣ High-order in FV is tricky (when compared to FD)
▪volume-averaged quantities (quadrature rules)
▪preserving conservation w/o losing accuracy
▪higher the order, larger the stencil
▪high-order temporal update (ODE solvers, e.g., RK3, RK4, etc.)
2D stencil for
2nd order PLM
2D stencil for
3rd order PPM

33. Stability, Consistency and Convergence
‣Lax Equivalence Theorem (for linear problem, P. Lax, 1956)
▪The only convergent schemes are those that are both consistent and stable.
▪Hard to show that the numerical solution converges to the original
solution of PDE; relatively easy to show consistency and stability of
numerical schemes
‣In practice, non-linear problems adopts the linear theory as guidance.
▪code verification (code-to-code comparison)
▪code validation (code-to-experiment, code-to-analytical solution
comparisons)
▪self-convergence test over grid resolutions (a good measurement for
numerical accuracy)

34. Shu-Osher Problem:1D Mach 3 Shock

35. Various Reconstructions

36. Circularly Polarized Alfven Wave
▪A CPAW problem propagates
smoothly varying oscillations of
the transverse components of
velocity and magnetic field.
▪The initial condition is the exact
nonlinear solutions of the MHD
equations.
▪The decay of the max of Vz and
Bz is solely due to numerical
dissipation: direct measurement
of numerical diffusion (Ryu, Jones
Frank, ApJ, 1995; Toth 2000, Del
Zanna et al. 2001; Gardiner
Stone 2005, 2008).
A. Mignone et al. / Journal of Computational Physics 229 (2010) 5896–5920 5907
Source: Mignone Tzeferacos, 2010, JCP
Fig. A.3. Long term decay of circularly polarized Alfvén waves after 16.5 time units, corresponding to ) 100 wave periods. In the left panel, we plot the
maximum value of the vertical component of velocity as a function of time for the WENO $ Z (solid line) and WENO + 3 (dashed line) schemes. For

37. Performance Comparison
L1 norm error
avg. comp.
time / step
0.221 (x5/3)sec 38.4 sec
32 256
Source: Mignone Tzeferacos, 2010, JCP
▪PPM (overall 2nd
order): 2h42m50s
▪MP5 (5th order):
15s(x5/3)=25s
▪More computational
work less memory
▪Better suited for HPC
▪Easier in FD; harder in FV
▪High-orders schemes are
better in preserving
solution accuracy on
AMR.

38. Truncation Errors at Fine-Coarse Boundary
Ff,L
i1/2,j+1/4
DF =
(i⇤, j) i1/2,j
Ff,L
i1/2,j1/4
Fc,R
U
t
1
x
=
1
x
+ r · F = TE =
h
Fc,R
i+1/2,j −
1
2
(Ff,L
i1/2,j+1/4 + Ff,L
h
F
#
(i + 1/2)x, jy
$
− F
#
(i − 1/2)x, jy
(
O(h) at F/C boundary
O(h2) otherwise
i1/2,j1/4)
i
$
+ O(y2)
✓Any 2nd order Scheme becomes 1st order at fine-coarse boundaries.
✓The deeper AMR level, the worse truncation errors accumulated and solutions
will become 1st order almost everywhere if grid pattern changes frequently.
✓High-order scheme is NOT just an option! (see papers by Colella et al.)
i
=
@F
@x
+ O(h), assuming x ⇡ y(= h)

39. Multidimensional Formulation
‣ 2D discrete difference equation in conservation form:
Un+1
i,j = Un
i,j
t
x
(Fn
i+1/2,j Fn
‣ Two different approaches:
‣ directionally “split” formulation
i1/2,j)
t
y
(Gn
i,j+1/2 Gn
i,j1/2)
‣ update each spatial direction separately, easy to implement, robust
‣ always good?
‣ directionally “unsplit” formulation
‣ update both spatial directions at the same time, harder to
implement
‣ you gain improved extra bonus (i.e., stability) from what you pay
for!

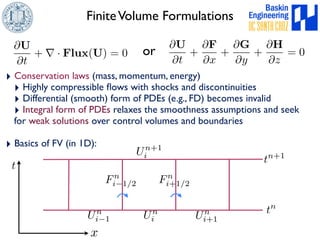
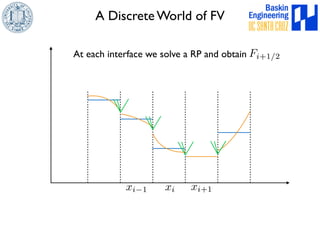
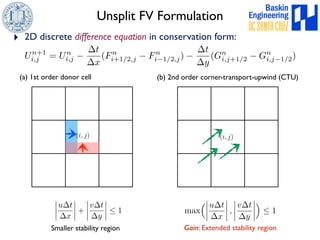
40. Unsplit FV Formulation
‣ 2D discrete difference equation in conservation form:
Un+1
i,j = Un
i,j
ut
x
[Un
i,j Un
i1,j ]
vt
y
[Un
i,j1] Un+1
i,j Un
i,j = Un
i,j
ut
x
[Un
i,j Un
i1,j ]
vt
y
[Un
i,j Un
i,j1]
+
t2
2
n u
x
⇥ v
y
(Un
i,j Un
i,j1)
v
y
(Un
i1,j Un
i1,j1)
⇤
+
v
y
⇥ v
y
(Un
i,j Un
i1,j)
v
y
(Un
i,j1 Un
i1,j1)
⇤o
Extra cost for corner coupling!
(a) 1st order donor cell
(i, j)
Un+1
i,j = Un
i,j
t
x
(Fn
i+1/2,j Fn
i1/2,j)
t
y
(Gn
i,j+1/2 Gn
i,j1/2)
(b) 2nd order corner-transport-upwind (CTU)
(i, j)

41. Unsplit FV Formulation
‣ 2D discrete difference equation in conservation form:
Un+1
i,j = Un
i,j
t
x
(Fn
i+1/2,j Fn
i1/2,j)
t
y
(Gn
i,j+1/2 Gn
i,j1/2)
(a) 1st order donor cell
ut
x
(i, j)
+
vt
y
(b) 2nd order corner-transport-upwind (CTU)
 1 max
⇣
(i, j)
ut
x
,
vt
y
⌘
 1
Smaller stability region Gain: Extended stability region

42. Unsplit vs. Split
✓Single-mode RT instability (Almgren et al.
ApJ, 2010)
✓Split solver:
High-wavenumber instabilities grow due to
experiencing high compression and expansion
in each directional sweep.
✓Unsplit solver:
High-wavenumber instabilities are suppressed
and do not grow.
✓ For MHD, it is more crucial to use unsplit in
order to preserve divergence-free solenoidal
constraint (Lee Deane, 2009; Lee, 2013):
Split PPM
Unsplit PPM
r · B =
@Bx
@x
+
@By
@y
+
@Bz
@z
= 0

43. Unsplit vs. Split
unsplit PPM split PPM

44. Excellent Resources

45. Last Episode
1. High Performance Computing
2. Ideas on Numerical Methods
3. Validation Predictive Science

46. In Collaboration with
U of Chicago:
D. Q. Lamb
P. Tzeferacos
N. Flocke
C. Graziani
K. Weide
U of Oxford:
G. Gregori
J. Meinecke

47. To Investigate B-field in the Universe
• In the universe, shocks are driven when two or more giant galaxy clusters are
merging together by gravitational collapsing.
• Mass accretion onto these clusters generate high Mach number shocks.
• These shocks can form a tiny “seed” magnetic fields which can then be amplified
by turbulent dynamo processes.
Filaments
Clusters
Voids
Expanding
Shocks
Courtesy of F. Miniati (ETH)
Courtesy of A. Kravtsov
U of Chicago

48. Shock Waves In SNR
Cool
Ejecta
Shocked
Ejecta
due to
Reverse Shocks
• Narrow X-ray filaments (~ parsec in
width) at the outer shock rim are
produced by synchrotron radiation
from ultra-relativistic electrons.
• The B-fields in the outer region ~
100μG or more.
Inner Region
Forward
Shock
Wave
Circumstellar
Gas
Outer Region
• The interior of the SNR Cassiopeia A contains a disordered shell of radio
synchrotron emission by giga-electronvolt electrons.
•The inferred magnetic field in these radio knots is a few milli-gauss, about 100
times larger than the surrounding interstellar gas.

49. Biermann Battery Mechanism
• The origin of the magnetic fields in the universe is still not yet
fully understood.
• Generalized Ohm’s law:
The BBT is the mostly widely invoked
mechanism to produce B fields from
unmagnetized plasma condition
, where J = r ⇥ B
(1) dynamo term
(2) resistive term
(3) Hall term
(4) Biermann battery term (BBT)
E =−
u ⇥ B
c
+ ⌘J
+
J ⇥ B
cnee
− rpe
nee

50. Takeaway
@B
@t
BBT
= crPe ⇥rne
qen2e
• BBT generates B fields when
gradients of electron pressure
and density are not aligned.
• BBT is zero in 1D (or
symmetric) flow or at spherical
shocks.
• BBT becomes non-zero when
symmetry is broken, and two
gradients are not aligned to each
other, that is, at downstream of
BBT = 0 BBT≠0 asymmetric shock.
We use laser to drive asymmetric shocks!
Please see our new study on BBT: Graziani et al., submitted to ApJ, 2014

51. Magnetic Fields in HEDP
Tzeferacos et al.,
HEDP, 2014, Accepted
Meinecke et al.,
Nature Physics, 2014

52. Investigating B-field in the Universe
300$J$1ns$ 3cm$
$2ω$
3,axis$coils$
Ar$(1atm)$
4cm$
Carbon$rod$
4cm$
In collaboration with
the research teams in
U of Chicago Oxford Univ.
Experimental Configuration

53. Investigating B-field in the Universe
In collaboration with
the research teams in
U of Chicago Oxford Univ.
3D Simulation

54. Validation Predictive Science
• We used five Vulcan laser shots (280-300J) to calibrate the fraction of the
laser energy deposited in the carbon rod target.
• With the calibrated amount of laser energy deposition we predicted the
shock radius of six laser shots with energies ranging from 200-343J.
breakout)shock)
material)
discon2nuity)
shock)
shock)generated)B
laser5target)B
t=50ns
Laserenergyrangeusedtocalibrateε

55. Validation Predictive Science
Experimental,data,
FLASH,
shock,radius,(mm),
t,(μs),
Meinecke et al.,
Nature Physics, 2-14

56. Summary
▪Novel ideas of numerical algorithms can play the key fundamental
role in many areas in modern science.
▪Computational mathematics is one of the corner stone research
areas that can provide major predictive scientific tools.
▪Numerical simulations can help designing better scientific
directions in wide ranges of research applications, especially in
physical science and engineering.

57. Thanks! Questions?
Dongwook Lee:
dlee79@ucsc.edu
ams.soe.ucsc.edu/people/dongwook
FLASH:
www.flash.uchicago.edu

58. Supplementary Slides

59. Relavant Questions
‣ What is scientific computing?
‣ How do we want to use computer for it?
‣ What should we do in order to use computing
resources in a better way?
‣ Can numerical algorithms and computational
mathematics improve computations?
‣ High-performance computing: petascale (or exascale ?)

60. Various Reconstruction
1st
2nd
3rd
5th
200 cells
1st on 400 cells
1st on 800 cells
1st + HLL
1st + HLLC
1st + Roe
200 cells

61. Low-Order vs. High-Order
1st Order
High-Order
Ref. Soln
1st order: 3200 cells (50 MB), 160 sec, 3828 steps
vs.
High-order: 200 cells (10 MB), 9 sec, 266 steps