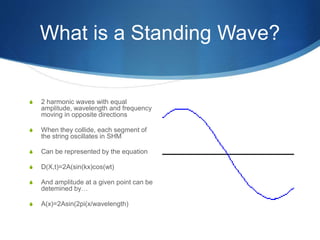
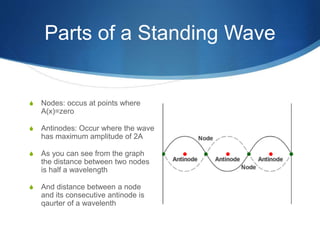
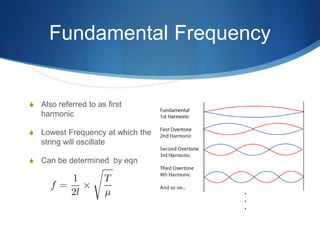
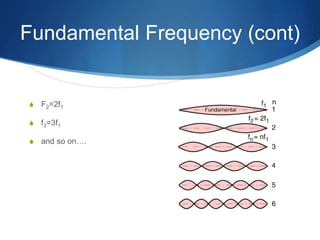
A standing wave is formed by two harmonic waves of equal amplitude, wavelength and frequency moving in opposite directions. When they collide, each segment of the string oscillates in simple harmonic motion (SHM). Nodes occur where the amplitude is zero, and antinodes occur where the amplitude is at a maximum of 2A. The fundamental frequency is the lowest frequency at which a string will oscillate, and higher harmonics are integer multiples of this frequency. Standing waves in instruments like flutes and guitars are responsible for producing musical notes. The document provides an example of calculating the wave speed, length, and first three harmonic frequencies of a guitar string with given properties.

1. S
Standing Waves and
Strings
Christopher Cheng 32929144

2. What is a Standing Wave?
S 2 harmonic waves with equal
amplitude, wavelength and frequency
moving in opposite directions
S When they collide, each segment of
the string oscillates in SHM
S Can be represented by the equation
S D(X,t)=2A(sin(kx)cos(wt)
S And amplitude at a given point can be
detemined by…
S A(x)=2Asin(2pi(x/wavelength)

3. Parts of a Standing Wave
S Nodes: occus at points where
A(x)=zero
S Antinodes: Occur where the wave
has maximum amplitude of 2A
S As you can see from the graph
the distance between two nodes
is half a wavelength
S And distance between a node
and its consecutive antinode is
qaurter of a wavelenth

4. Fundamental Frequency
S Also referred to as first
harmonic
S Lowest Frequency at which the
string will oscillate
S Can be determined by eqn

5. Fundamental Frequency (cont)
S F2=2f1
S f3=3f1
S and so on….

6. For an explanation of standing
waves watch from 1:10- 2:00

7. Standing Waves in
Instruments
S The formation of standing
waves is what’s responsible for
producing musical notes
S Eg. Flutes, sound waves
propagate and when they reach
the end, they reflect back,
creating notes.
S But sounds that are created by
instruments are the result of
many different frequencies.

8. Question
S A Guitar String has a linear mass density of 4.5x10-4 kg/m
and has a tension of 80N. It takes 8.7x10-4 s for the string
to travel from one end to the other
S What is the wavespeed of the string?
S How long is the string?
S What is the frequency of the first three Harmonic

9. Solution
S What is the wavespeed of the string?
S V=(T/u)(1/2)
S V=(80/4.5x10-4)0.5=421.6 m/s

10. Solution #2
S Delta t = (L/V)
S 8.7x104s=(L/421.61 m/s)
S L= 0.36m

11. Solution #3
S Using the equation on the right
and substituting values we find
that the fundamental frequency
is 585.6hz
S Second harmonic= 2f1= 1171hz
S Third harmonic=3f1=1756.8hz