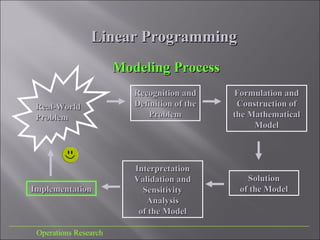
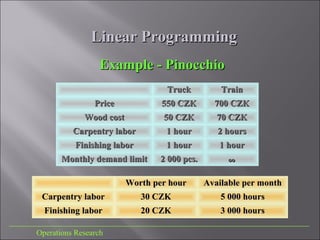
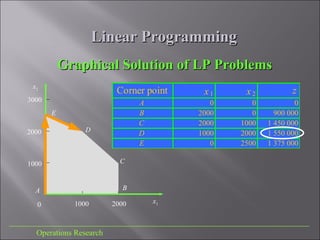
This document discusses linear programming, which is a technique in operations research for optimizing a linear objective function subject to linear constraints. It describes the modeling process, provides an example of maximizing profit from producing two products with limited resources, and discusses graphically representing and solving linear programming problems and interpreting their optimal solutions.

1. ___________________________________________________________________________
Operations Research
Linear ProgrammingLinear Programming

2. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Modeling ProcessModeling Process
Real-WorldReal-World
ProblemProblem
Recognition andRecognition and
Definition of theDefinition of the
ProblemProblem
Formulation andFormulation and
Construction ofConstruction of
the Mathematicalthe Mathematical
ModelModel
SolutionSolution
of the Modelof the Model
InterpretationInterpretation
Validation andValidation and
SensitivitySensitivity
AnalysisAnalysis
of the Modelof the Model
ImplementationImplementation

3. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
 linear objective functionlinear objective function
 linear constraintslinear constraints
 decision variablesdecision variables
Mathematical ModelMathematical Model
 maximizationmaximization
 minimizationminimization
 equationsequations ==
 inequalitiesinequalities ≤≤ oror ≥≥
 nonnegativity constraintsnonnegativity constraints

4. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Example - PinocchioExample - Pinocchio
 2 types of wooden toys:2 types of wooden toys: trucktruck
traintrain
 Inputs:Inputs: wood - unlimitedwood - unlimited
carpentry labor – limitedcarpentry labor – limited
finishing labor - limitedfinishing labor - limited
 Objective:Objective: maximize total profit (revenue – cost)maximize total profit (revenue – cost)
 Demand:Demand: trucks - limitedtrucks - limited
trains - unlimitedtrains - unlimited

5. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Example - PinocchioExample - Pinocchio
TruckTruck TrainTrain
PricePrice 550 CZK550 CZK 700 CZK700 CZK
Wood costWood cost 50 CZK50 CZK 70 CZK70 CZK
Carpentry laborCarpentry labor 1 hour1 hour 2 hours2 hours
Finishing laborFinishing labor 1 hour1 hour 1 hour1 hour
Monthly demand limitMonthly demand limit 2 000 pcs.2 000 pcs. ∞∞
Worth per hourWorth per hour Available per monthAvailable per month
Carpentry laborCarpentry labor 30 CZK30 CZK 5 000 hours5 000 hours
Finishing laborFinishing labor 20 CZK20 CZK 3 000 hours3 000 hours

6. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Graphical Solution of LP ProblemsGraphical Solution of LP Problems
Feasible areaFeasible area
Objective functionObjective function
Optimal solutionOptimal solution
x1
x2
z

7. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Graphical Solution of LP ProblemsGraphical Solution of LP Problems
Feasible area - convex setFeasible area - convex set
A set of pointsA set of points SS is ais a convex setconvex set if the line segment joiningif the line segment joining
any pair of points inany pair of points in SS is wholly contained inis wholly contained in SS..
Convex polyhedronsConvex polyhedrons

8. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Graphical Solution of LP ProblemsGraphical Solution of LP Problems
Feasible area – corner pointFeasible area – corner point
A pointA point PP in convex polyhedronin convex polyhedron SS is ais a corner pointcorner point if it doesif it does
not lie on any line joining any pair of other (thannot lie on any line joining any pair of other (than PP) points in) points in
SS..

9. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research© Jan Fábry
Graphical Solution of LP ProblemsGraphical Solution of LP Problems
Basic Linear Programming TheoremBasic Linear Programming Theorem
The optimal feasible solution, if it exists, will occurThe optimal feasible solution, if it exists, will occur
at one or more of the corner points.at one or more of the corner points.
Simplex methodSimplex method

10. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Graphical Solution of LP ProblemsGraphical Solution of LP Problems
1000
3000
x1
x2
20000
A
2000
1000
B
C
D
E
Corner point x1 x2 z
A 0 0 0
B 2000 0 900 000
C 2000 1000 1 450 000
D 1000 2000 1 550 000
E 0 2500 1 375 000

11. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Interpretation of Optimal SolutionInterpretation of Optimal Solution
 Decision variablesDecision variables
 Binding / Nonbinding constraint (Binding / Nonbinding constraint (≤≤ oror ≥≥))
 Objective valueObjective value
= 0= 0
Slack/SurplusSlack/Surplus
variablevariable
> 0> 0
Slack/SurplusSlack/Surplus
variablevariable

12. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Special Cases of LP ModelsSpecial Cases of LP Models
Unique Optimal SolutionUnique Optimal Solution
z
x1
x2
A

13. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Special Cases of LP ModelsSpecial Cases of LP Models
Multiple Optimal SolutionsMultiple Optimal Solutions
z
x1
x2
B
C

14. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Special Cases of LP ModelsSpecial Cases of LP Models
No Optimal SolutionNo Optimal Solution
z
x1
x2

15. Linear ProgrammingLinear Programming
___________________________________________________________________________
Operations Research
Special Cases of LP ModelsSpecial Cases of LP Models
NoNo FeasibleFeasible SolutionSolution
x1
x2