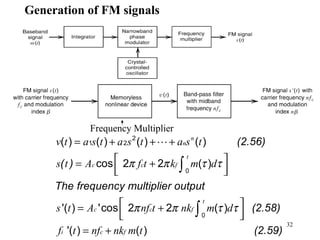
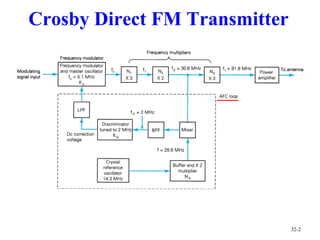
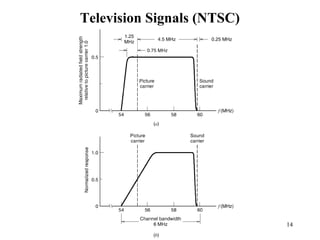
This document summarizes continuous-wave modulation techniques. It discusses amplitude modulation (AM), including the transmitter and receiver, and limitations of AM. It also covers linear modulation schemes like double sideband-suppressed carrier, single sideband, and vestigial sideband modulation. Frequency modulation techniques are analyzed, including narrowband and wideband FM. Bessel functions are used to describe the spectrum of wideband FM signals. Carson's rule and universal curves are presented for calculating the transmission bandwidth of FM signals.

1. 1
Chapter 2 Continuous-Wave Modulation
2.1 Introduction

2. 2
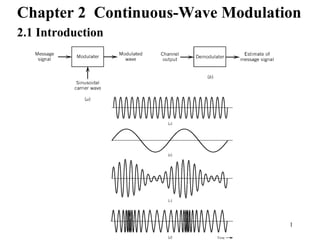
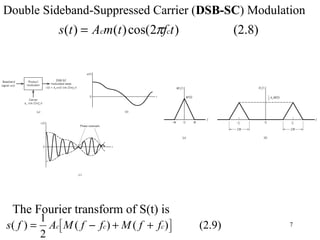
2.2 Consider a carrier
The output of the modulator
Where m(t) is the baseband signal , ka is the amplitude sensitivity.
(2.1))2cos()( tfAtc cc π=
[ ] (2.2))2cos()(1)( tftmkAts cac π+=
)(offreqencyhightesttheiswhere
(2.4).2
(2.3)tallfor,1)(.1
tmW
Wf
tmk
c
a
>>
<
X
1+kam(t) S(t
)
Accos(2πfct)

3. 3
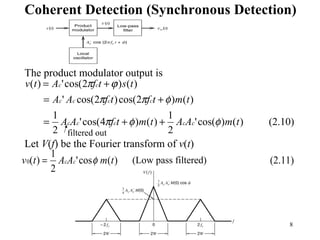
Recall
1.Negative frequency component of m(t) becomes visible.
2.fc-W < M(f) < fc lower sideband
fc < M(f) < fc+W upper sideband
3.Transmission bandwidth BT=2W
(2.2))2cos()()2cos()( tftmkAtfAts caccc ππ +=
[ ]
[ ]
[ ] [ ]
)(ofTransformFouriertheis)(where
(2.5))()(
2
)()(
2
)(
)()(
2
1
)2cos()(
)()(
2
1
)2cos(
tmfM
ffMffM
Ak
ffff
A
fs
ffMffMtftm
fffftf
cc
ca
cc
c
ccc
ccc
++−+++−=
++−⇔
++−⇔
δδ
π
δδπ

4. 4
Virtues and Limitations of Amplitude Modulation
Transmitter
Receiver
Major limitations
1.AM is wasteful of power.
2.AM is wasteful of bandwidth.

5. 5
2.3 Linear Modulation Schemes
Linear modulation is defined by
Three types of linear modulation:
1.Double sideband-suppressed carrier (DSB-SC) modulation
2.Single sideband (SSB) modulation
3.Vestigial sideband (VSB) modulation
componentQuadrature)(
componentphase-In)(
(2.7))2sin()()2cos()()(
=
=
−=
ts
ts
tftstftsts
Q
I
cQcI ππ

6. 6
Notes:
1.sI(t) is solely dependent on m(t)
2.sQ(t)is a filtered version of m(t).
The spectral modification of s(t) is solely due to sQ(t).

7. 7
Double Sideband-Suppressed Carrier (DSB-SC) Modulation
The Fourier transform of S(t) is
(2.8))2cos()()( tftmAts cc π=
(2.9))()(
2
1
)( 



++−= ccc ffMffMAfs

8. 8
Coherent Detection (Synchronous Detection)
The product modulator output is
Let V(f) be the Fourier transform of v(t)
(2.10))()cos('
2
1
)()4cos('
2
1
)()2cos()2cos('
)()2cos(')(
tmAAtmtfAA
tmtftfAA
tstfAtv
ccccc
cccc
cc
φφπ
φππ
ϕπ
++=
+=
+=
(2.11))(cos'
2
1
)(0 tmAAtv cc φ=
filtered out
(Low pass filtered)

9. 9
Costas Receiver
I-channel and Q-channel are coupled together to
form a negative feedback system to maintain synchronization
The phase control signal ceases with modulation.
1
4
2 2 2 2
2 2
0
1 1
cos sin ( ) ( )sin(2 )
4 8
( ) (sin2 2 )
c c
c
A m t A m t
A m t
φ
φ φ φ
φ φ φ
≈
=
≈ ≈
(multiplier +
very narrow band LF)

10. 10
Quadrature-Carrier Multiplexing (or QAM)
Two DSB-SC signals occupy the same channel
bandwidth, where pilot signal (tone ) may be
needed.
)2sin()()2cos()()( 21 tftmAtftmAts cccc ππ +=

11. 11
Single-Sideband Modulation (SSB)
The lower sideband and upper sideband of AM signal
contain same information .
The frequency-discrimination method consists of a
product modulator (DSB-SC) and a band-pass filter.
The filter must meet the following requirements:
a.The desired sideband lies inside the passband.
b.The unwanted sideband lies inside the stopband.
c.The transition band is twice the lowest frequency of
the message.
To recover the signal at the receiver, a pilot carrier or a stable oscillator
is needed (Donald Duck effect ).

12. 12
Vestigial Sideband Modulation (VSB)
When the message contains near DC component
The transition must satisfy
(2.14)
(2.13)for1)()(
:linearisresponsephaseb.The
1)()(.a
fWB
WfWffHffH
ffHffH
νT
cc
cc
+=
≤≤−=++−
=++−

13. 13
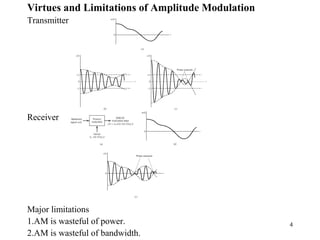
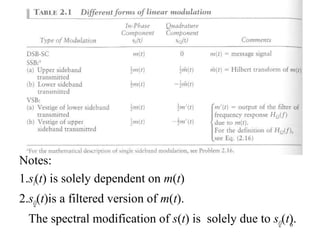
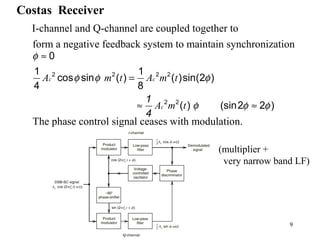
± corresponds to upper or lower sideband
(2.15))2sin()('
2
1
)2cos()(
2
1
)( tftmAtftmAts cccc ππ ±=
HQ(f)
m(t) m’(t)
[ ] (2.16)for)()()( WfWffHffHjfH ccQ ≤≤−+−−=

14. 14
Television Signals (NTSC)

15. 15
2.4 Frequency Translation
Up conversion
f2=f1+fl, fl=f2-f1
Down conversion
f2=f1-fl , fl=f1-f2
cos(2 )A f tπl l

16. 16
2.5 Frequency-Division Multiplexing (FDM)

17. 17
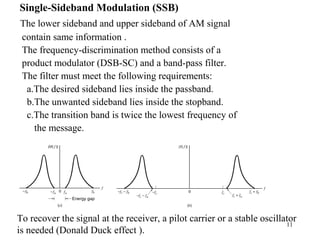
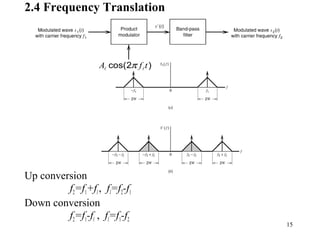
2.6 Angle Modulation
Basic Definitions:
Better discrimination against noise and interference
(expense of bandwidth).
The instantaneous frequency is
[ ] (2.19))(cos)( tAts ic θ=
constantiswhere
(2.22)2)(
is)(carrier,dunmodulateanFor
(2.21)
)(
2
1
2
)()(
lim
)(lim)(
0Δ
Δ
0Δ
c
cci
i
i
ii
t
t
t
i
tft
t
dt
td
t
ttt
tftf
φ
φπθ
θ
θ
π
π
θθ
+=
=




∆
−∆+
=
=
→
→

18. 18
1. Phase modulation (PM)
2. Frequency Modulation (FM)
[ ] (2.23))(2cos
modulatortheofysensitivitphase:
)(2)(
tmktfAs(t)
k
tmktft
pcc
p
pci
+=
+=
π
πθ
(2.24)
ππ
ππ (2.26)
:frequency sensitivity of the modulator
compare (2.23) and (2.26)
0
0
( ) ( )
( ) 2 2 ( )
cos 2 2 ( )
i c f
t
i c f
t
c c f
f
p
f t f k m t
t f t k m d
s(t) A f t k m d
k
k m'
θ τ τ
τ τ
= +
= +
 = +
  
⇒
∫
∫
π
0
2 ( )
t
f(t) k m dτ τ= ∫
(2.25)
generating FM signal generating PM signal

19. 19
2.7 Frequency Modulation
FM is a nonlinear modulation process , we can not apply
Fourier transform to have spectral analysis directly.
1.Consider a single-tone modulation which produces a
narrowband FM (kf is small)
2.Next consider a single-tone and wideband FM
(kf is large)
deviationfrequency:Δ
(2.28))2cos(
)2cos()(
(2.27))2cos()(let
mf
mc
mmfci
mm
Akf
tfff
tfAkftf
tfAtm
=
∆+=
+=
=
π
π
π (deterministic)

20. 20
[ ]
radian.onenlarger thais,FMWideband
radian.oneansmaller this,FMNarrowband
(2.33))2sin(2cos)(
(2.32))2sin(2)(
(2.31)indexModulation
(2.30))2sin(2
)(2)((2.25),Recall
0
β
β
πβπ
πβθ
β
π
ττπθ
tftfAts
tftπft
f
f
tf
f
f
tπf
dft
mcc
mci
m
m
m
c
t
ii
+=
+=
∆
=
∆
+=
= ∫
(2.19) =>

21. 21
Narrowband FM
[ ]
[ ] [ ]
[ ]
[ ]
(2.35))2sin()2sin()2cos()(
)2sin()2sin(sin
1)2sin(cos
small,isBecause
)34.2()2sin(sin)2sin()2sin(cos)2cos(
)2sin(2cos)(
tftfAtfAts
tftf
tf
tftfAtftfA
tftfAts
mcccc
mm
m
mccmcc
mcc
ππβπ
πβπβ
πβ
β
πβππβπ
πβπ
−≈
≈
≈
−=
+=

22. 22
The output of Fig 2.21 is
s(t) differs from ideal condition in two
respects:
1.The envelope contains a residual AM.
(FM has constant envelope)
2.θi(t) contains odd order harmonic distortions
For narrowband FM, ≤ 0.3 radians.
)2sin()()2cos()(' tfdmkAtfAts cfccc πττπ ∫−=
)
!7!5!3
(sin
753
+−+−=
xxx
xx
β

23. 23
[ ] [ ]{ }
[ ]
[ ] [ ]{ } (2.37))(2cos)(2cos
2
1
)2(cos
)2cos()2(cos)2(cos
(2.2))2(cos)(1)(
)2cos()(,wavemodulatingsinusoidalAM withFor
(2.36))(2cos)(2cos
2
1
)2(cos
(2.35))2)sin(2(sin)2(cos)(
(2.35)Recall
AM
tfftffAtfA
tftfAktfA
tftmkAts
tftm
tfftffAtfA
tftfAtfAts
mcmcccc
mccacc
cac
m
mcmcccc
mcccc
−−++=
+=
+=
=
−−++≈
−≈
ππµπ
πππ
π
π
ππβπ
ππβπ
Narrow band FM
AM

24. 24
Wideband FM (large B)
[ ]
[ ]
[ ]
[ ]
(2.40))2exp()(~
)]2sin(exp[)(~
bydefinedenvelopecomplextheis)(~
andpartrealthedenotesRewhere
(2.38)))(2exp()(~Re
))2sin(2exp(Re)(
sincosexp
(2.33))2sin(2cos)(
∑
∞
−∞=
=
=
=
+=
+=
+=
n
mn
mc
c
mcc
mcc
tnfjcts
tfjAts
ts
tfjts
tfjtfjAts
xjx(jx)
tftfAts
π
πβ
π
πβπ
πβπ
(2.39)
Complex Fourier Transform

25. 25
[ ]
[ ]
(2.41)
Let (2.42)
1
2
1
2
1
2
1
2
( )exp( 2 )
exp sin(2 ) 2 )
2
exp ( sin )
2
m
m
m
m
f
n m mf
f
m c m mf
m
c
n
c f s t j nf t dt
f A j f t j nf t dt
x f t
A
c j x nx dx
π
β π π
π
β
π
−
−
= −
= −
=
= −
∫
∫
%
[ ]
2
(2.43)
Define the th order Bessel function of the first kind as
A3, x
(2.44)
2
2 2
2
( ) 0)
1
( ) exp ( sin )
2
( )
( ) ( )
n
n c n
c n
n
n
d y dy
x x n y
dx dx
J j x nx dx
c A J
s t A J
π
π
π
π
β β
π
β
β
−
−
=−
+ + − =
= −
=
=
∫
∫
% (2.45)exp( 2 )mj nf tπ
∞
∞
∑

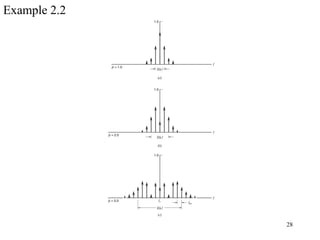
26. 26
[ ]
[ ]
[ ] (2.49))()()(
2
)(
is)(ofransformFourier tThe
(2.48))(2cos)(
(2.47))(2exp)(Re)(
mcmcn
c
mcnc
mcnc
nfffnfffJ
A
fS
ts
tnffJA
tnffjJAts
+++−−=
+=






+=
∑
∑
∑
∞
∞−
∞
∞−
∞
∞−
δδβ
πβ
πβ
Figure 2.23 Plots of Bessel functions of the first kind for varying

27. 27
-
Properties of ( )
1. ( ) ( 1) ( ), for all (2.50)
2.If is small
( ) 1
( )
2
( ) 0 2 (2.51)
3. ( ) 1
Observation o
0
1
2
n
n
n n
n
n
J
J J n
J
J
J n
J
β
β β
β
β
β
β
β
β
−
∞
∞
= −
≈
≈
≈ >
=∑
f FM
1.An FM signal contains components.
2.For small , the FM signal is effectively composed of a carrier and
a single pair of side freqencies at narrowband FM
3.The am
2 3 ,c m m m
c m
f , f , f , f
f f
β
± ⇒

plitude of carrier depends on
A
(2.54)
2
2 21
( )
2 2
c
c nP A J
β
β
∞
−∞
= = ∑

28. 28
Example 2.2

29. 29
Transmission Bandwidth of FM signals
With a specified amount of distortion , the FM signal is
effectively limited to a finite number of significant side
frequencies.
A.Carson’s rule
, = , (2.55)
1
2 2 2 (1 )T m m
m
f
B f f f f f
f
β β
β
∆
≈ ∆ + = ∆ + ∆ =

30. 30
B. , ( ) 0.01 ,maxmax max2 2T m n T
f
B n f J B nβ
β
∆
= >> =
Universal curve for evaluating the 1 percent bandwidth of an FM wave

31. 31
Example 2.3
In north America, the maximum value of frequency deviation is
fixed at 75kHz for commercial FM broadcasting by radio. If we take
the modulation frequency W=15kHz, which is typically the
“maximum” audio frequency of interest in FM transmission, we find
that corresponding value of the deviation ratio is
Using Carson’s rule of Equation (2.55) , replacing by D , and
replacing fm by W , the approximate value of the transmission
bandwidth of the FM signal is obtained as
BT=2(75+15)=180kHz
On the other hand , use of the curve of Figure 2.26 gives the
transmission bandwidth of the FM signal to be
BT=3.2 =3.2x75=240kHz
In practice , a bandwidth of 200kHz is allocated to each FM
transmission . On this basis , Carson’s rule underestimates the
transmission bandwidth by 10 percent , whereas the universal curve
of Figure 2.26 overestimates it by 20 percent.
5
15
75
D ==
f∆
β
f∆

32. 32
Generation of FM signals
(2.56)
( )
The frequency multiplier output
(2.58)
2
1 2
0
0
( ) ( ) ( ) ( )
cos 2 2 ( )
'( ) 'cos 2 2 ( )
'( ) ( )
n
n
t
c c f
t
c c f
i c f
v t a s t a s t a s t
s t A f t k m d
s t A nf t nk m d
f t nf nk m t
π π τ τ
π π τ τ
= + + +
 = +
  
 = +
  
= +
∫
∫
L
(2.59)
Frequency Multiplier

33. Varactor diode VCO FM modulator
32-1

34. Crosby Direct FM Transmitter
32-2