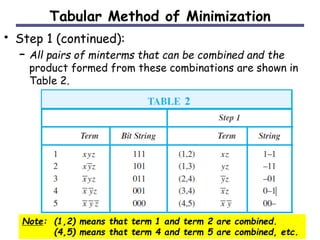
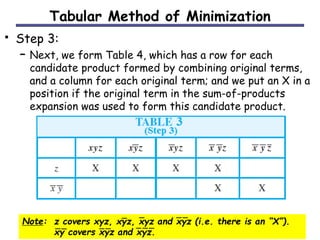
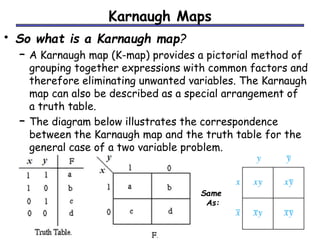
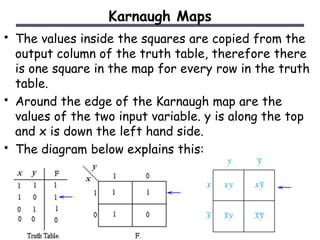
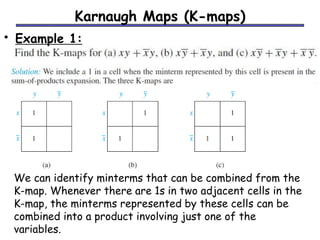
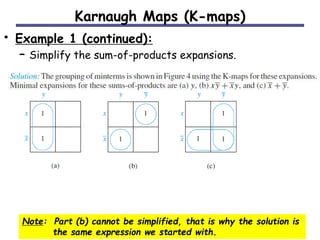
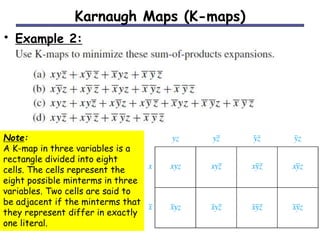
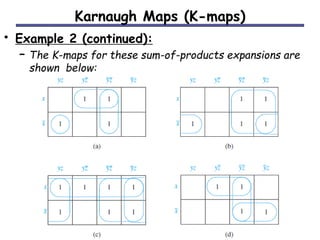
The document discusses different methods for minimizing Boolean functions, including algebraic manipulation, tabular methods, and Karnaugh maps. The tabular method involves grouping minterms based on their binary representations and combining terms that differ by one bit. Karnaugh maps provide a visual way to group adjacent minterms and identify prime implicants to find a minimized expression. Both methods aim to cover all minterms with the fewest prime implicants.

1. Minimization of Boolean Functions

2. What is Minimization?
• In mathematics, expressions are simplified for a
number of reasons, for instance simpler expression
are easier to understand and easier to write down,
they are also less prone to error in interpretation
but, most importantly, simplified expressions are
usually more efficient and effective when
implemented in practice.
• A Boolean expression is composed
of variables and terms. The simplification of
Boolean expressions can lead to more effective
computer programs, algorithms and circuits.

3. What is Minimization?
• Minimisation can be achieved by a
number of methods, three well known
methods are:
1. Algebraic Manipulation of Boolean
Expressions
2. Tabular Method of Minimization
3. Karnaugh Maps

4. 4
Algebraic Manipulation of Boolean Expressions
• We can now start doing some simplifications
x’y’ + xyz + x’y
= x’(y’ + y) + xyz [ Distributive: x’y’ + x’y = x’(y’ + y) ]
= x’1 + xyz [ complement: x’ + x = 1 ]
= x’ + xyz [ identity: x’1 = x’ ]
= (x’ + x)(x’ + yz) [ Distributive ]
= 1  (x’ + yz) [ complement: x’ + x = 1 ]
= x’ + yz [ identity]

5. 5
Algebraic Manipulation of Boolean Expressions
• Here are two
different but
equivalent
circuits.
• In general the
one with fewer
gates is
“better”:
– It costs less
to build
– It requires
less power
– But we had to
do some work
to find the
second form

6. Tabular Method of Minimization
• The tabular method which is also known as the
Quine-McCluskey method is particularly useful
when minimising functions having a large number of
variables, e.g. The six-variable functions. Computer
programs have been developed employing this
algorithm.
• The method reduces a function in standard sum of
products form to a set of prime implicants from
which as many variables are eliminated as possible.
• These prime implicants are then examined to see if
some are redundant.
Note: A prime implicant is a product term which cannot be further
simplified by combination with other terms.

7. Tabular Method of Minimization
• We will show how the Quine–McCluskey method can
be used to find a minimal expansion
equivalent to:
• We will represent the minterms in this expansion
by bit strings. The first bit will be 1 if x occurs and
0 if x occurs. The second bit will be 1 if y occurs
and 0 if y occurs. The third bit will be 1 if z occurs
and 0 if z occurs.
• We then group these terms according to the
number of 1s in the corresponding bit strings. This
information is shown in Table 1.

8. Tabular Method of Minimization

9. Tabular Method of Minimization
• Step 1:
– Minterms that can be combined are those that differ in
exactly one literal. Hence, two terms that can be
combined differ by exactly one in the number of 1s in the
bit strings that represent them.
– When two minterms are combined into a product, this
product contains two literals. A product in two literals is
represented using a dash to denote the variable that
does not occur.
– For instance, the minterms xyz and x yz, represented by
bit strings 101 and 001, can be combined into yz,
represented by the string _01.

10. Tabular Method of Minimization
• Step 1 (continued):
– All pairs of minterms that can be combined and the
product formed from these combinations are shown in
Table 2.
Note: (1,2) means that term 1 and term 2 are combined.
(4,5) means that term 4 and term 5 are combined, etc.

11. Tabular Method of Minimization
• Step 2:
– Next, all pairs of products of two literals that can be
combined are combined into one literal. Two such
products can be combined if they contain literals for the
same two variables, and literals for only one of the two
variables differ.
– In terms of the strings representing the products, these
strings must have a dash in the same position and must
differ in exactly one of the other two slots.
– We can combine the products yz and yz, represented by
the strings _11 and _01, into z, represented by the string
_ _1.

12. Tabular Method of Minimization
• Step 2 (continued):
– We show all the combinations of terms that can be
formed in this way in Table 3.
Note: (1,2,3,4) means that terms (1,2) and (3,4) are combined
OR
terms (1,3) and (2,4) are combined.

13. Tabular Method of Minimization
• Step 3:
– In Table 3 we also indicate which terms have been used
to form products with fewer literals; these terms will not
be needed in a minimal expansion.
– The next step is to identify a minimal set of products
needed to represent the Boolean function.
– We begin with all those products that were not used to
construct products with fewer literals.

14. Tabular Method of Minimization
• Step 3:
– Next, we form Table 4, which has a row for each
candidate product formed by combining original terms,
and a column for each original term; and we put an X in a
position if the original term in the sum-of-products
expansion was used to form this candidate product.
Note: z covers xyz, xyz, xyz and xyz (i.e. there is an “X”).
xy covers xyz and xyz.

15. Tabular Method of Minimization
• Step 3 (continued):
– In this case, we say that the candidate product covers
the original minterm. We need to include at least one
product that covers each of the original minterms.
– Consequently, whenever there is only one X in a column in
the table, the product corresponding to the row this X is
in must be used.
– From Table 4 we see that both z and x y are needed.
– Hence, the final answer is z + x y.

16. Karnaugh Maps
• So far we can see that applying Boolean algebra can
be awkward in order to simplify expressions.
• Apart from being laborious (and requiring the
remembering all the laws) the method can lead to
solutions which, though they appear minimal, are
not.
• The Karnaugh map provides a simple and straight-forward
method of minimising boolean expressions.
• With the Karnaugh map Boolean expressions having
up to four and even six variables can be simplified.

17. Karnaugh Maps
• So what is a Karnaugh map?
– A Karnaugh map (K-map) provides a pictorial method of
grouping together expressions with common factors and
therefore eliminating unwanted variables. The Karnaugh
map can also be described as a special arrangement of
a truth table.
– The diagram below illustrates the correspondence
between the Karnaugh map and the truth table for the
general case of a two variable problem.
Same
As:

18. Karnaugh Maps
• The values inside the squares are copied from the
output column of the truth table, therefore there
is one square in the map for every row in the truth
table.
• Around the edge of the Karnaugh map are the
values of the two input variable. y is along the top
and x is down the left hand side.
• The diagram below explains this:

19. Karnaugh Maps (K-maps)
• Example 1:
We can identify minterms that can be combined from the
K-map. Whenever there are 1s in two adjacent cells in the
K-map, the minterms represented by these cells can be
combined into a product involving just one of the
variables.

20. Karnaugh Maps (K-maps)
• Example 1 (continued):
– For instance, and are represented by adjacent
cells and can be combined into , because
– Moreover, if 1s are in all four cells, the four minterms
can be combined into one term, namely, the Boolean
expression 1 that involves none of the variables.
– We circle blocks of cells in the K-map that represent
minterms that can be combined and then find the
corresponding sum of products.
– The goal is to identify the largest possible blocks, and to
cover all the 1s with the fewest blocks using the largest
blocks first and always using the largest possible blocks.

21. Karnaugh Maps (K-maps)
• Example 1 (continued):
– Simplify the sum-of-products expansions.
Note: Part (b) cannot be simplified, that is why the solution is
the same expression we started with.

22. Karnaugh Maps (K-maps)
• Example 2:
Note:
A K-map in three variables is a
rectangle divided into eight
cells. The cells represent the
eight possible minterms in three
variables. Two cells are said to
be adjacent if the minterms that
they represent differ in exactly
one literal.

23. Karnaugh Maps (K-maps)
• Example 2 (continued):
– The K-maps for these sum-of-products expansions are
shown below:

24. Karnaugh Maps (K-maps)
• Example 2 (continued):
– The grouping of blocks shows that minimal expansions
into Boolean sums of Boolean products are:
Note:
In part (d) note that the prime implicants xz and x y are essential
prime implicants, but the prime implicant yz is not essential,
because the cells it covers are covered by the other two prime
implicants.