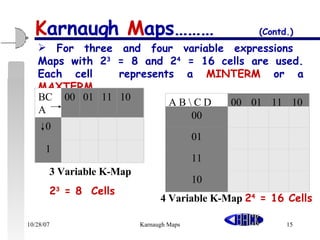
The document discusses the minimization of Boolean expressions using Karnaugh maps (K-maps). It explains that K-maps provide an alternative graphical method for simplifying logic circuits by arranging the 1s and 0s from a truth table. The key steps involve drawing the K-map based on the number of variables, entering the function values, forming the largest possible groups of adjacent 1s, and selecting the minimum number of groups needed to cover all 1s while avoiding redundancy. Examples demonstrate how octet, quad, pair and single cell reductions can minimize expressions by reducing the number of literals. Rules for valid groupings using K-maps in simplifying expressions are also outlined.

1. By Ms. Nita Arora, PGT Computer Science Kulachi Hansraj Model School e -Lesson

2. Subject : Computer Science (083) Unit : Boolean Algebra Topic : Minimization of Boolean Expressions Using Karnaugh Maps (K-Maps) Category : Senior Secondary Class : XII

3. L earning O bjectives : After successfully completing this module students should be able to: Understand the Need to simplify (minimize) expressions List Different Methods for Minimization Karnaugh Maps Algebraic method Use Karnaugh Map method to minimize the Boolean expression

4. P revious K nowledge : The students should be familiar with the following terms in Boolean Algebra before going through this module on K-MAPS Boolean variable, Constants and Operators Postulates of Boolean Algebra Theorems of Boolean Algebra Logic Gates- AND, OR, NOT, NAND, NOR Boolean Expressions and related terms MINTERM (Product Term) MAXTERM (Sum Term) Canonical Form of Expressions x y x+y

5. Minimization Of Boolean Expressions Who Developed it NEED For Minimization Different Methods What is K-Map Drawing a K-Map Minimization Steps Important Links Recap . K-Map Rules (SOP Exp.) K-Map Quiz EXIT Karnaugh Maps INDEX

6. References For K-Map Minimizer Download http:// karnaugh.shuriksoft.com Thomas C. Bartee, DIGITAL COMPUTER FUNDAMENTALS, McGraw Hill International. Computer Science (Class XII) By Sumita Arora http://www.ee.surrey.ac.uk/Projects/Labview/minimisation/karrules.html

7. The End

8. Boolean expressions are practically implemented in the form of GATES (Circuits). A minimized Boolean expression means less number of gates which means Simplified Circuit M INIMIZATION OF B OOLEAN E XPRESSION WHY we Need to simplify (minimize) expressions?

9. M INIMIZATION OF B OOLEAN E XPRESSION Different methods Karnaugh Maps Algebraic Method

10. K arnaugh M aps WHAT is Karnaugh Map (K-Map)? A special version of a truth table Karnaugh Map (K-Map) is a GRAPHICAL display of fundamental terms in a Truth Table . Don’t require the use of Boolean Algebra theorems and equation Works with 2,3,4 (even more) input variables (gets more and more difficult with more variables) NEXT

11. K-maps provide an alternate way of simplifying logic circuits. One can transfer logic values from a Truth Table into a K-Map. The arrangement of 0’s and 1’s within a map helps in visualizing, leading directly to Simplified Boolean Expression K arnaugh M aps……… (Contd.) NEXT

12. Correspondence between the Karnaugh Map and the Truth Table for the general case of a two Variable Problem Truth Table 2 Variable K-Map K arnaugh M aps……… (Contd.) A B 0 0 0 1 1 0 1 1 F a b c d A \ B 0 1 0 a b 1 c d The diagram below illustrates the correspondence between the Karnaugh map and the truth table for the general case of a two variable problem. Truth Table Karnaugh Map A \ B 0 1 0 a b 1 c d

13. D rawing a K arnaugh M ap (K-Map) K-map is a rectangle made up of certain number of SQUARES For a given Boolean function there are 2 N squares where N is the number of variables (inputs) In a K-Map for a Boolean Function with 2 Variables f(a,b) there will be 2 2 =4 squares Each square is different from its neighbour by ONE Literal Each SQUARE represents a MAXTERM or MINTERM NEXT

14. Karnaugh maps consist of a set of 2 2 squares where 2 is the number of variables in the Boolean expression being minimized. Truth Table 2 Variable K-Map K arnaugh M aps……… (Contd.) 1 The diagram below illustrates the correspondence between the Karnaugh map and the truth table for the general case of a two variable problem. Truth Table Karnaugh Map A \ B 0 1 0 0 1 1 1 1 A B F 0 0 0 0 1 1 1 0 1 1 1 1 Minterm A’B’ A’B A B’ A B Maxterm A + B A + B’ A’ + B A’ + B’ NEXT

15. For three and four variable expressions Maps with 2 3 = 8 and 2 4 = 16 cells are used. Each cell represents a MINTERM or a MAXTERM 4 Variable K-Map 2 4 = 16 Cells K arnaugh M aps……… (Contd.) 3 Variable K-Map 2 3 = 8 Cells The diagram below illustrates the correspondence between the Karnaugh map and the truth table for the general case of a two variable problem. Truth Table Karnaugh Map BC A 00 01 11 10 0 1 A B \ C D 00 01 11 10 00 01 11 10

16. M inimization S teps (SOP Expression with 4 var.) The process has following steps: Draw the K-Map for given function as shown Enter the function values into the K-Map by placing 1's and 0's into the appropriate Cells 1 1 1 1 A B \ C D 00 01 11 10 00 0 0 0 1 0 3 0 2 01 0 0 0 0 11 1 1 0 0 10 1 1 0 0 0 5 0 4 0 7 0 6 0 0 12 13 15 14 8 9 11 10 NEXT

17. M inimization S teps (SOP Expression) Form groups of adjacent 1's . Make groups as large as possible. Group size must be a power of two. i.e. Group of 8 (OCTET), 4 (QUAD), 2 (PAIR) or 1 (Single) NEXT A B \ C D 00 01 11 10 00 0 0 0 1 0 3 0 2 01 0 0 0 0 11 1 1 0 0 10 1 1 0 0 0 5 0 4 0 7 0 6 0 0 12 13 15 14 8 9 11 10

18. M inimization S teps (SOP Expression) Select the least number of groups that cover all the 1's. Ensure that every 1 is in a group. 1's can be part of more than one group. Eliminate Redundant Groups 1 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 0 wx yz 00 01 11 10 00 01 11 10 3 2 4 5 7 6 1 12 13 15 14 8 9 11 10 NEXT

19. Example: Reduce f(wxyz)=Σ(1,3,4,5,7,10,11,12,14,15) PAIR (m4,m5) REDUNDANTGROUP 1 1 0 0 1 1 0 1 0 1 1 1 0 1 1 0 0 wx yz 00 01 11 10 00 01 11 10 3 2 4 5 7 6 1 12 13 15 14 8 9 11 10 QUAD (m1,m3,m5,m7) QUAD (m10,m11,m14,m15) QUAD (m3,m7,m11,m15) REDUNDANT Group PAIR (m4,m12) Minimized Expression : xy’z’ + wy + w’z

20. OCTET REDUCTION ( Group of 8:) OCTET (m0,m1,m4,m5,m8, m9, m12,m13) The term gets reduced by 3 literals i.e. 3 variables change within the group of 8 ( Octets ) 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 W X YZ 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X NEXT

21. OCTET REDUCTION ( Group of 8:) OCTET (m1,m3,m5,m7,m9, m11, m13,m15) 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 W X YZ 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X NEXT

22. OCTET REDUCTION ( Group of 8:) MAP ROLLING OCTET (m0,m2,m4,m6, m8, m10, m12,m14) 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 W X YZ 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10 NEXT

23. OCTET REDUCTION ( Group of 8:) OCTET (m4,m5,m6,m7,m12, m13, m14,m15) 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 W X YZ 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10 NEXT

24. OCTET REDUCTION ( Group of 8:) MAP ROLLING OCTET (m0,m1,m2,m3 M8,m9,m10,m11) 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 W X YZ 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10

25. QUAD REDUCTION ( Group of 4) 1 1 0 0 1 1 1 1 0 1 1 1 0 1 1 0 0 WX YZ 3 2 4 5 7 6 1 12 13 15 14 8 9 11 10 QUAD (m1,m3,m5,m7) QUAD (m10,m11,m14,m15) QUAD (m4,m5,m12,m13) 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X The term gets reduced by 2 literals i.e. 2 variables change within the group of 4( QUAD ) NEXT

26. QUAD REDUCTION ( Group of 4) MAP ROLLING QUAD (m1,m3,m9,m11) QUAD (m4,m6,m12,m14) 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 0 0 WX YZ 3 2 4 5 7 6 1 12 13 15 14 8 9 11 10 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X NEXT

27. QUAD REDUCTION ( Group of 4) QUAD (m0,m2,m8,m10) CORNER ROLLING 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 WX YZ 3 2 4 5 7 6 1 12 13 15 14 8 9 11 10 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X

28. SINGLE CELL REDUCTION SINGLE CELL (m1) SINGLE CELL (m12) QUAD (m10,m11,m14,m15) The term is not reduced in a single cell 1 1 0 0 1 1 0 1 0 0 0 0 0 0 1 0 wx yz 00 01 11 10 00 01 11 10

29. PAIR REDUCTION ( Group of 2) YZ MAP ROLLING PAIR (m0,m2) The term gets reduced by 1 literals i.e. 1 variables change within the group of 2( PAIR ) 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 WX 3 2 4 5 7 6 1 12 13 15 14 8 9 11 10 PAIR (m5,m7) 0 0 0 1 1 1 1 0 Y.Z Y.Z Y. Z Y. Z 0 0 W.X 0 1 W.X 1 1 W.X 1 0 W.X

30. Groups may not include any cell containing a zero Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

31. Groups may be horizontal or vertical, but not diagonal. Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

32. Groups must contain 1, 2, 4, 8, or in general 2 n cells. That is if n = 1, a group will contain two 1's since 2 1 = 2. If n = 2, a group will contain four 1's since 2 2 = 4. Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

33. Each group should be as large as possible. Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

34. Each cell containing a 1 must be in at least one group. Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

35. Groups may overlap. Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

36. Groups may wrap around the table. The leftmost cell in a row may be grouped with the rightmost cell and The top cell in a column may be grouped with the bottom cell . Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

37. There should be as few groups as possible , as long as this does not contradict any of the previous rules. Karnaugh Maps - Rules of Simplification (SOP Expression) NEXT

38. No 0’s allowed in the groups. No diagonal grouping allowed. Groups should be as large as possible. Only power of 2 number of cells in each group. Every 1 must be in at least one group. Overlapping allowed. Wrap around allowed. Fewest number of groups are considered. Redundant groups ignored Karnaugh Maps - Rules of Simplification (SOP Expression)

39. Minimalization logic function with 3-10inputs. Draw karnaugh map Draw shema Cońvert to NOR and NANDS. Karnaugh map minimalization software is freeware. Important Links… K-Min Karnaugh Minimizer is a tool for developers of small digital devices and radio amateurs, also for those who is familiar with Boolean algebra, mostly for electrical engineering students.

40. Who Developed K-Maps… Name : Maurice Karnaugh, a telecommunications engineer at Bell Labs. While designing digital logic based telephone switching circuits he developed a method for Boolean expression minimization. Year : 1950 same year that Charles M. Schulz published his first Peanuts comic.