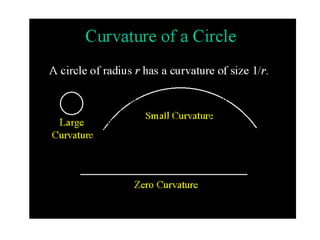
The curvature of a circle is defined as 1/r, where r is the radius of the circle. Therefore, smaller circles have higher curvature and larger circles have lower curvature. The curvature of a straight line is 0, since straight lines are considered "flat" with no curvature.

1. A circle of radius r has a curvature of size 1/r.
Therefore, small circles have large curvature
and large circles have small curvature. The
curvature of a line is 0. In general, an object
with zero curvature is "flat."

2. Curvature
The act of curving
The state of being curved.
 The ratio of the change in the angle of a
tangent that moves along curve from
point to point
The limit of the ratio of the change in the
angle of a tangent as arc length
approaches zero
The reciprocal of the radius of a circle.

3. Let C:𝑟 = 𝑟(𝑠) be a space curve and P be a point on it,
then curvature at 𝑃 is defined as rate of rotation of
tangent (change in the direction of tangent) at 𝑃. Its
magnitude is denoted by 𝜅 (kappa) and defined by
𝛿𝜃 𝑑𝜃
𝜅 = 𝑙𝑖𝑚 𝛿𝑠 = 𝑑𝑠
𝛿𝑠 →0
Where 𝛿𝜃 is the angle between tangents at points 𝑃 and
𝑄 on the curve along arc length 𝛿𝑠.
tangent
𝛿𝜃
tangent
C:𝑟 = 𝑟(𝑠)

4. More precisely, curvature is
•Scalar measure of bending nature of the curve
•Degree of curving in a line
•Change in the direction of tangent line
•Arc rate of rotation of tangent line from point to point
•Change in principal normal along tangent direction

5. Curvature measures the rate at which a space curve 𝒓(t) changes direction.
The direction of curve is given by the unit tangent vector
𝒓(𝒕)
𝒕(𝒕) =
𝒓(𝒕)
which has length 1 and is tangent to 𝒓(t).
The picture below shows the unit tangent vector 𝒕 to the curve 𝒓(t) =(2cos(t), sin(t), 0)
at several points.
Obviously,
if 𝒓(t) is a straight line, the curvature is 0.
Otherwise the curvature is non-zero.
To be precise, curvature is defined to be the
magnitude of the rate of change of the unit
tangent vector with respect to arc length:
𝒅𝒕
𝒅𝒕
𝒌=
𝒅𝒓
𝒅𝒕

6. Note
1. Straight line has zero curvature
2. A circle has constant curvature
3. A circular helix has constant curvature
4. The curvature of small circle is large and vice versa
1
5. The radius of curvature is denoted by 𝜌, i.e 𝜅 = 𝜌