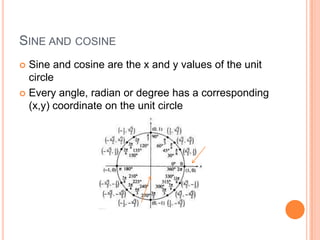
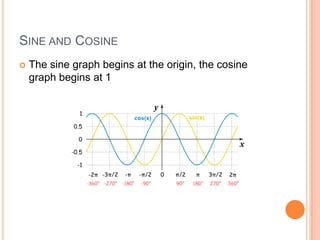
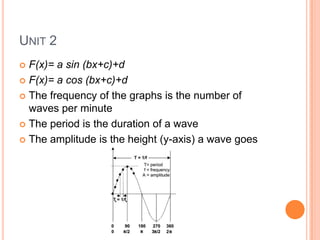
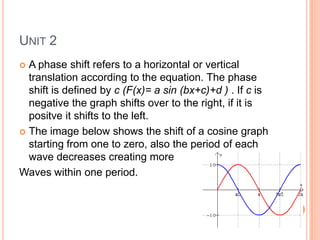
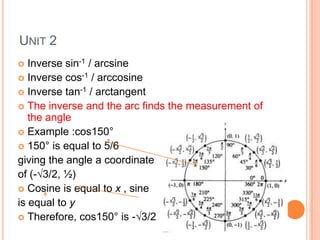
This document covers trigonometry units 1 and 2. It discusses measuring angles in degrees and radians, where a radian is equal to the arc length of the radius. It defines sine and cosine as the x and y values on the unit circle corresponding to an angle. It describes how to solve for sine and cosine given an angle and hypotenuse using trigonometric functions, Pythagorean theorem, and laws of sines and cosines. Unit 2 covers trigonometric functions involving amplitude, frequency, period, and phase shifts. It also discusses inverse trigonometric functions.

1. TRIGONOMETRY UNITS 1 &2
By Leslie Zamudio

2. HOW TO MEASURE IN BOTH DEGREES &
RADIANS
 An angle is an opening of a circle measured
in degrees & a radian is a measurement
that is equal to the length of the radius
which is the same as the arc length. Every
angle is equal to a radian. Multiplying any
radian by 180/∏

3. SINE AND COSINE
 Sine and cosine are the x and y values of the unit
circle
 Every angle, radian or degree has a corresponding
(x,y) coordinate on the unit circle

4. SINE AND COSINE
 The sine graph begins at the origin, the cosine
graph begins at 1

5. SOLVING FOR SINE AND COSINE
 Solving for sine and cosine, you need and angle
and the hypotenuse
 Plugging in what you know, can solve for other
sides and angles.
 Using the Pythagorean theorem and the Law of
Cosines and the Law of Sines, inverse cosine and
inverse sine may also help

6. UNIT 2
 F(x)= a sin (bx+c)+d
 F(x)= a cos (bx+c)+d
 The frequency of the graphs is the number of
waves per minute
 The period is the duration of a wave
 The amplitude is the height (y-axis) a wave goes

7. UNIT 2
 A phase shift refers to a horizontal or vertical
translation according to the equation. The phase
shift is defined by c (F(x)= a sin (bx+c)+d ) . If c is
negative the graph shifts over to the right, if it is
positve it shifts to the left.
 The image below shows the shift of a cosine graph
starting from one to zero, also the period of each
wave decreases creating more
Waves within one period.

8. UNIT 2
 Inverse sin-1 / arcsine
 Inverse cos-1 / arccosine
 Inverse tan-1 / arctangent
 The inverse and the arc finds the measurement of
the angle
 Example :cos150°
 150° is equal to 5/6
giving the angle a coordinate
of (-√3/2, ½)
 Cosine is equal to x , sine
is equal to y
 Therefore, cos150° is -√3/2