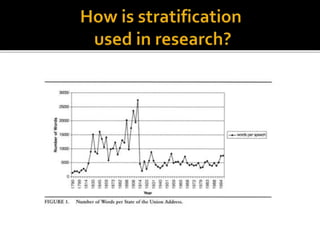
This document discusses key concepts related to populations and samples in social science research. It defines key terms like population, sample, parameter, and element. It also distinguishes between different sampling methods like probability sampling, non-probability sampling, stratified sampling, cluster sampling, and quota sampling. For each method, it provides examples and discusses their advantages and disadvantages. The goal is to help readers understand how to properly define a population, select a sample, and apply different sampling techniques in research.

1. POL / SOC 360-01
Spring 2015

4.  Definition of Population
 Population should be:
 Carefully and Fully Defined
 Relevant to Research Question
 Remember McDonald and Popkin study?
 How did they define their population?

5.  Definition of Sample
 Importance of Sample Data
 Quality of Sample Based on:
 Overall Sample Size
 How members chosen to be part of sample

6.  Advantages of Sample
 Time
 Money
 Disadvantages of Sample
 Less accurate
 Subject to error
 Decision made on practical grounds

7.  Population Parameter
 Characteristics about population quantified as a
number
▪ Examples: Proportion, Mean/Average, etc.
 Estimator
 Numerically estimates the value of population
characteristic, or population parameter

8.  Sample Statistic
 An estimator of a population parameter derived from a
population sample
 Element
 Also called a unit of analysis
 A single occurrence, realization, or instance of the
objects or entities being studied
▪ Examples: Individuals, States, Cities, Countries,
Speeches, Wars

9.  Stratum
 Population subdivided into groups of similar
elements before a sample is drawn
 Subgroup of a population sharing characteristics
 Examples:
 MSU students stratified by class, major, or GPA
 Latin Graduation Honors

12.  Sampling Frame
 Particular population from which sample is drawn
 Closer sampling frame is to population of interest or
theoretical population, the better off you are
 Example:The Literary Digest Poll?

13.  If sampling frame is incomplete or inappropriate, then
sample bias will occur
 Sample will be unrepresentative of the population,
and inaccurate conclusions may result
 Sample bias caused by a biased selection of elements,
even if frame is complete and accurate
 Sampling Unit
 Entity listed in a sampling frame

14.  Probability Sample
 Sample for which each element in the total
population has a known probability of being
included in sample
 Nonprobability Sample
 Sample in which each element in the total
population has an unknown probability of being
selected

16.  Each element and combination of elements has an
equal chance of being selected
 What has to happen for this to occur?
 Short Class Activity on Random Numbers

17.  Attempt to make draft process fairer
 How did the lottery process work?
 Selective Service (SS) estimated that anyone
with number higher than 200 would not be
called
 Found negative correlation between day of
birth and lottery number

18.  Random Numbers Generator

19.  Elements selected from list at predetermined
intervals (e.g. every Kth element)
 K = Sampling Interval or “skip” between elements
 Computed as Population Size (N) / Sample Size (n)
 Useful when dealing with long list of population
elements (e.g. all SC justices)
 Often used in product testing

20.  Probability sample where elements sharing
one or more characteristics are grouped
 Two MainTypes:
 Proportionate Sample
 Disproportionate Sample

21.  Stratified sample were each stratum
represented in proportion to its size in
population
 Example: Congress of the Future
 Sampling Fraction

22.  Stratified sample where each stratum is NOT
represented in proportion to size in population
 Issue ofWeighting

23.  Probability sample in which sampling frame
initially consists of clusters of elements
 Groups / clusters of elements are identified and
listed as sampling units
 Within each sampling unit, certain elements are
identified and sampled
 Example: Public Opinion Polling

24.  Advantages:
 Allows researchers to get around problem of
acquiring list of elements in target population
 Can reduce fieldwork costs
 Disadvantage:
 Greater level of imprecision

26.  Goal: To study a diverse and usually limited
number of observations
 Researcher exercises considerable discretion
 Example: Fenno and Home Style

27.  Elements are included because they are
convenient or easy for a researcher to study
 Used for exploratory research or when target
population is impossible to define / locate

28.  Sample in which elements are sampled in
proportion to their representation in
population
 Similar to proportionate stratified sampling,
but elements are quota sample are NOT
chosen in reasoned or probabilistic manner

30.  Initial respondents used to identify others
who might qualify for inclusion in sample
 Useful when trying to study members in
elusive population:
 Draft Dodgers
 Political Protestors
 Drug Users