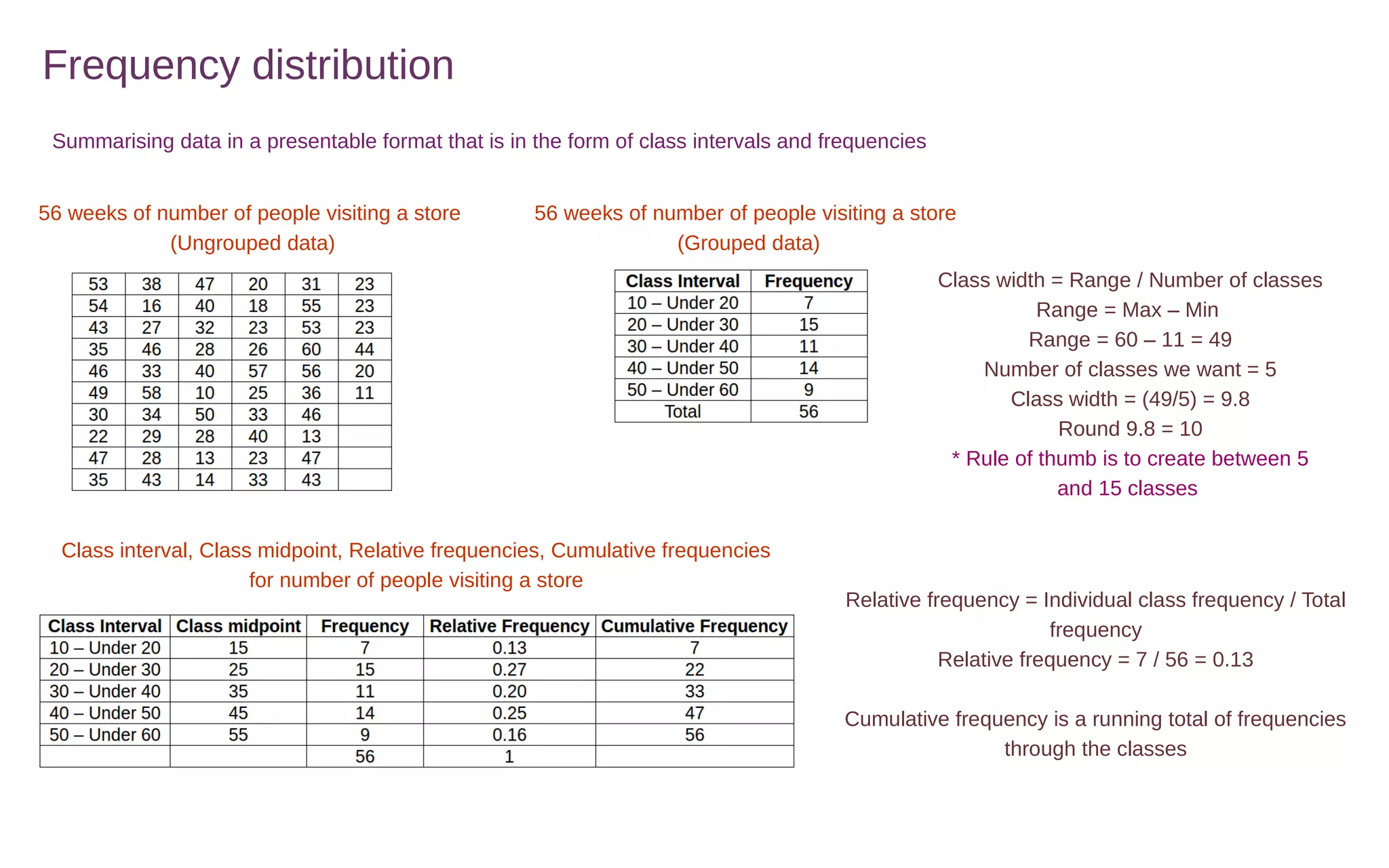
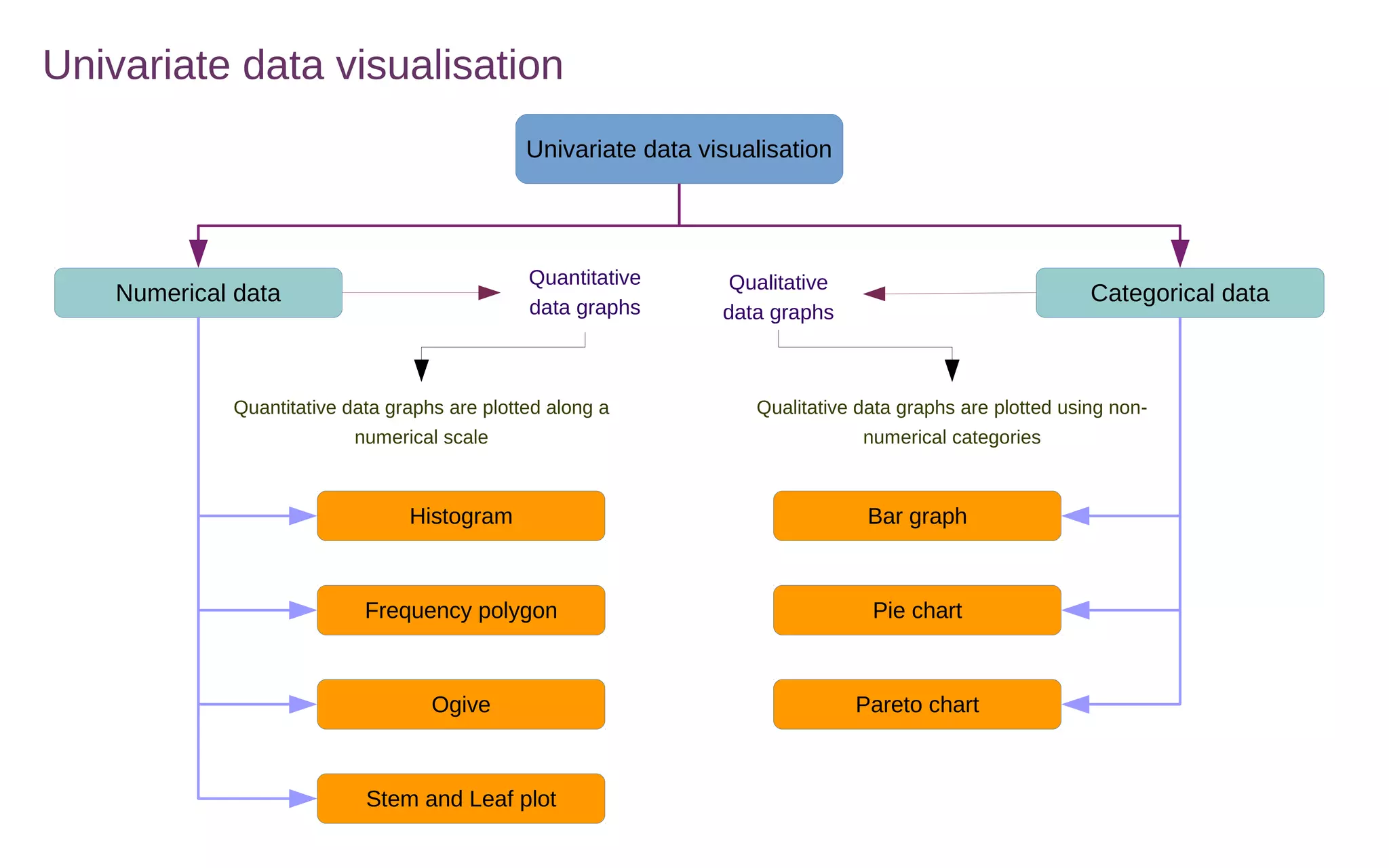
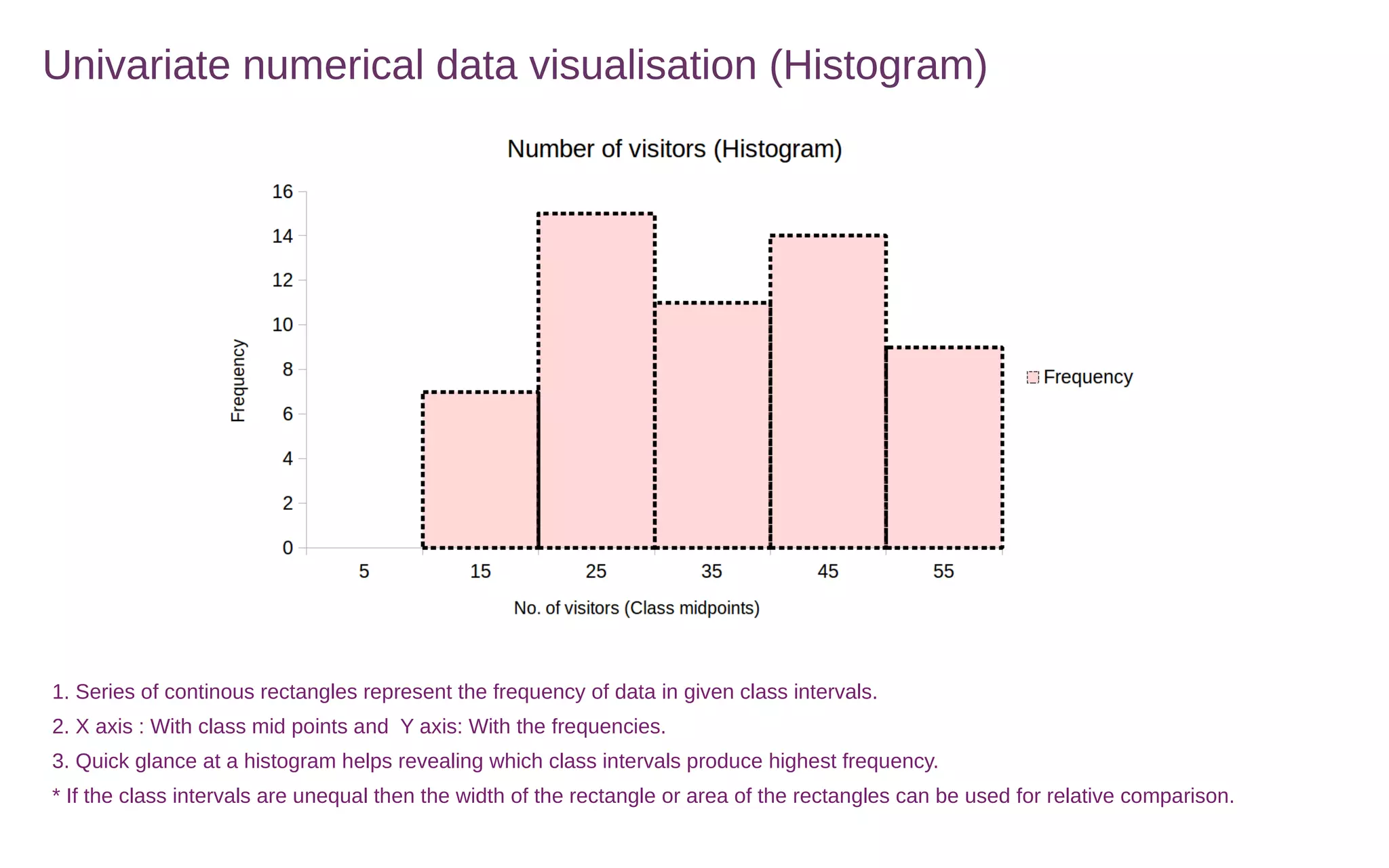
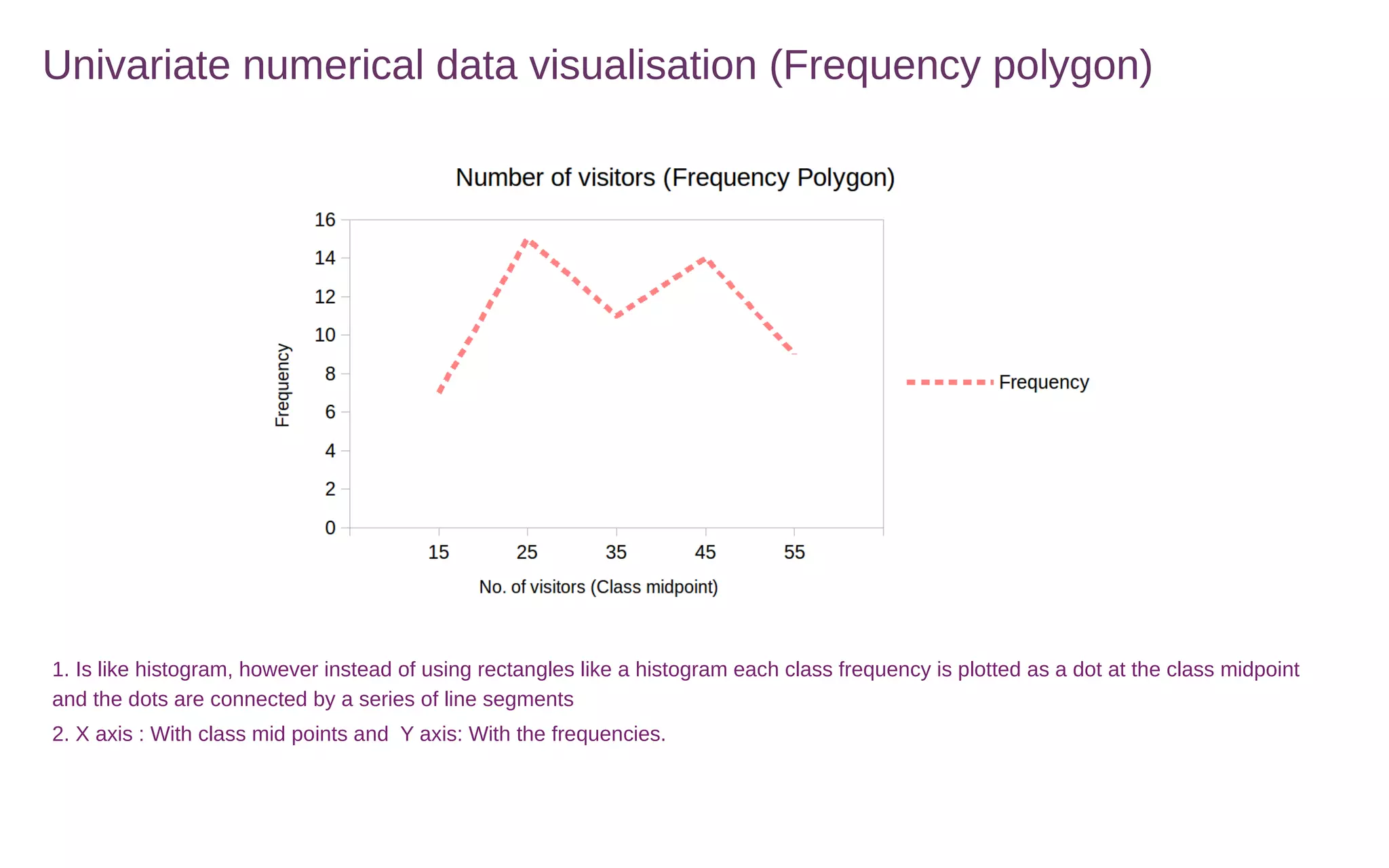
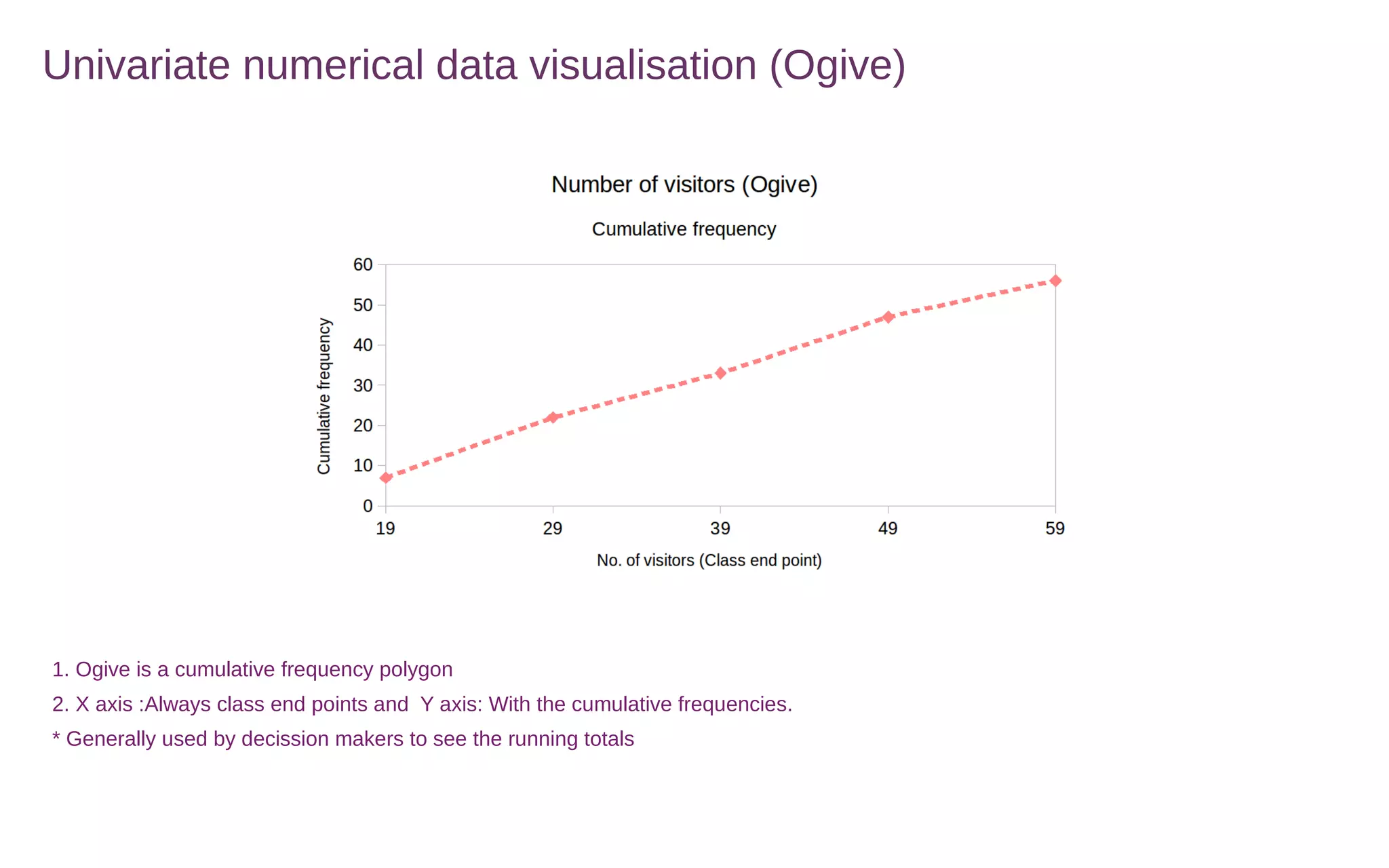
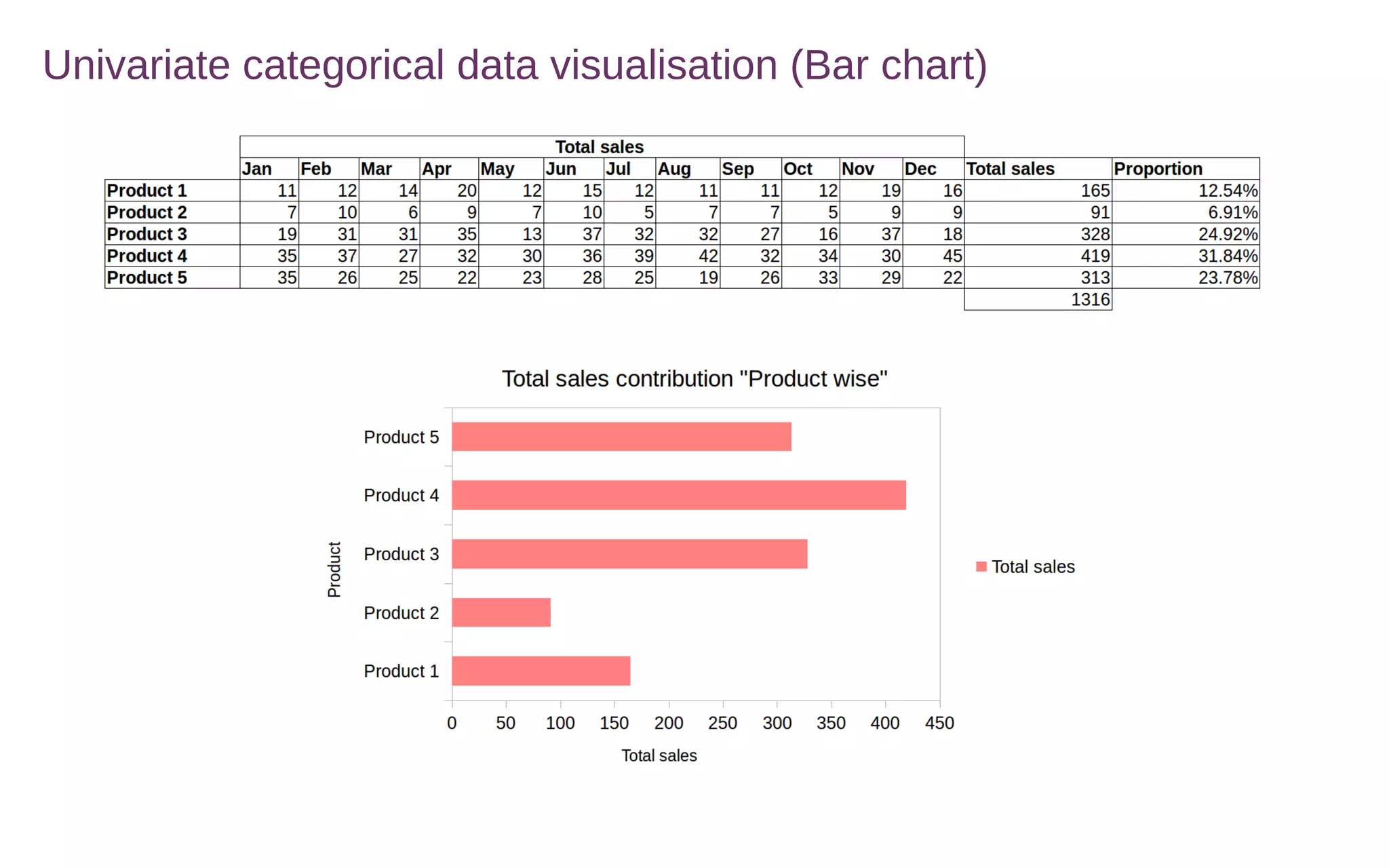
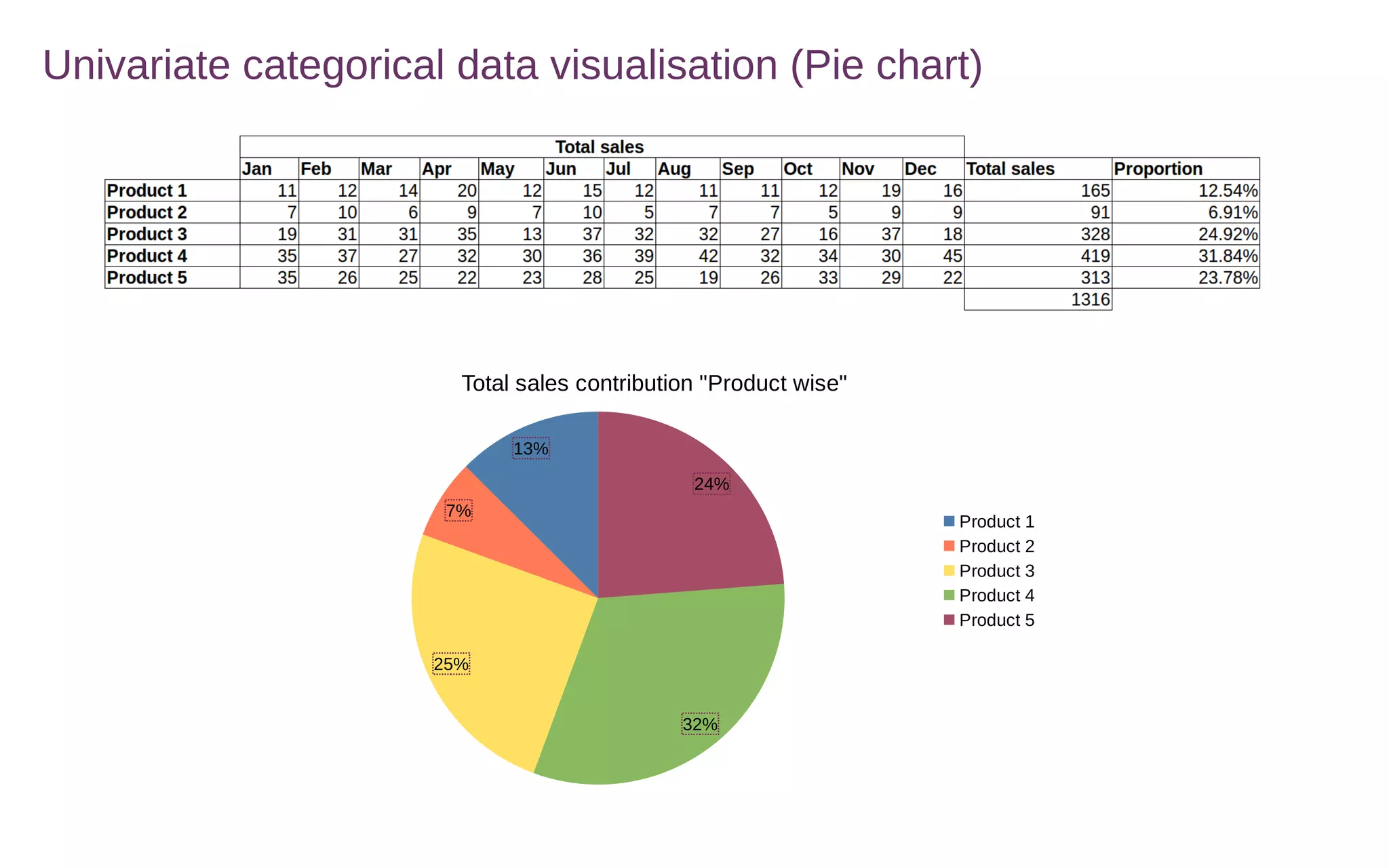
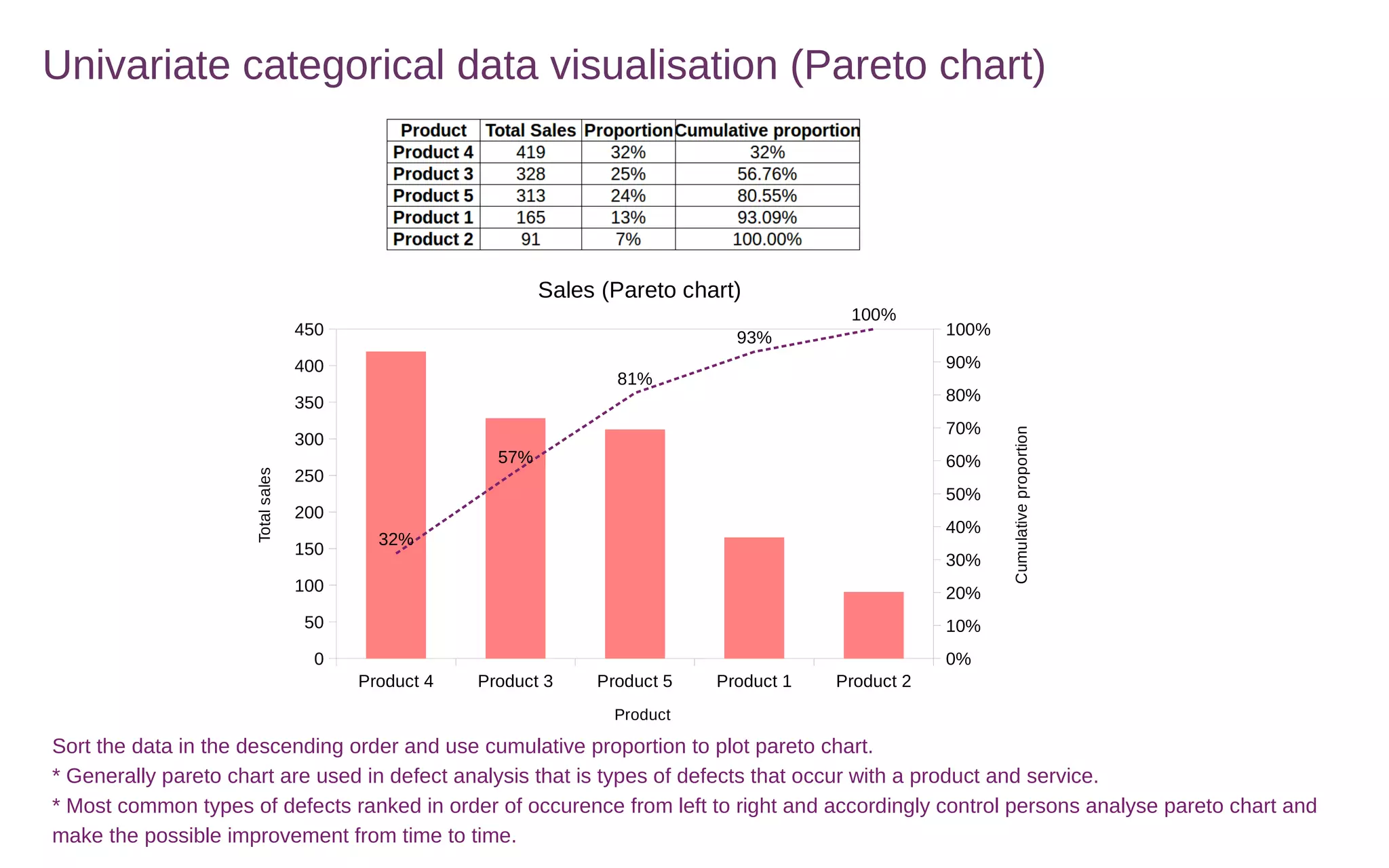
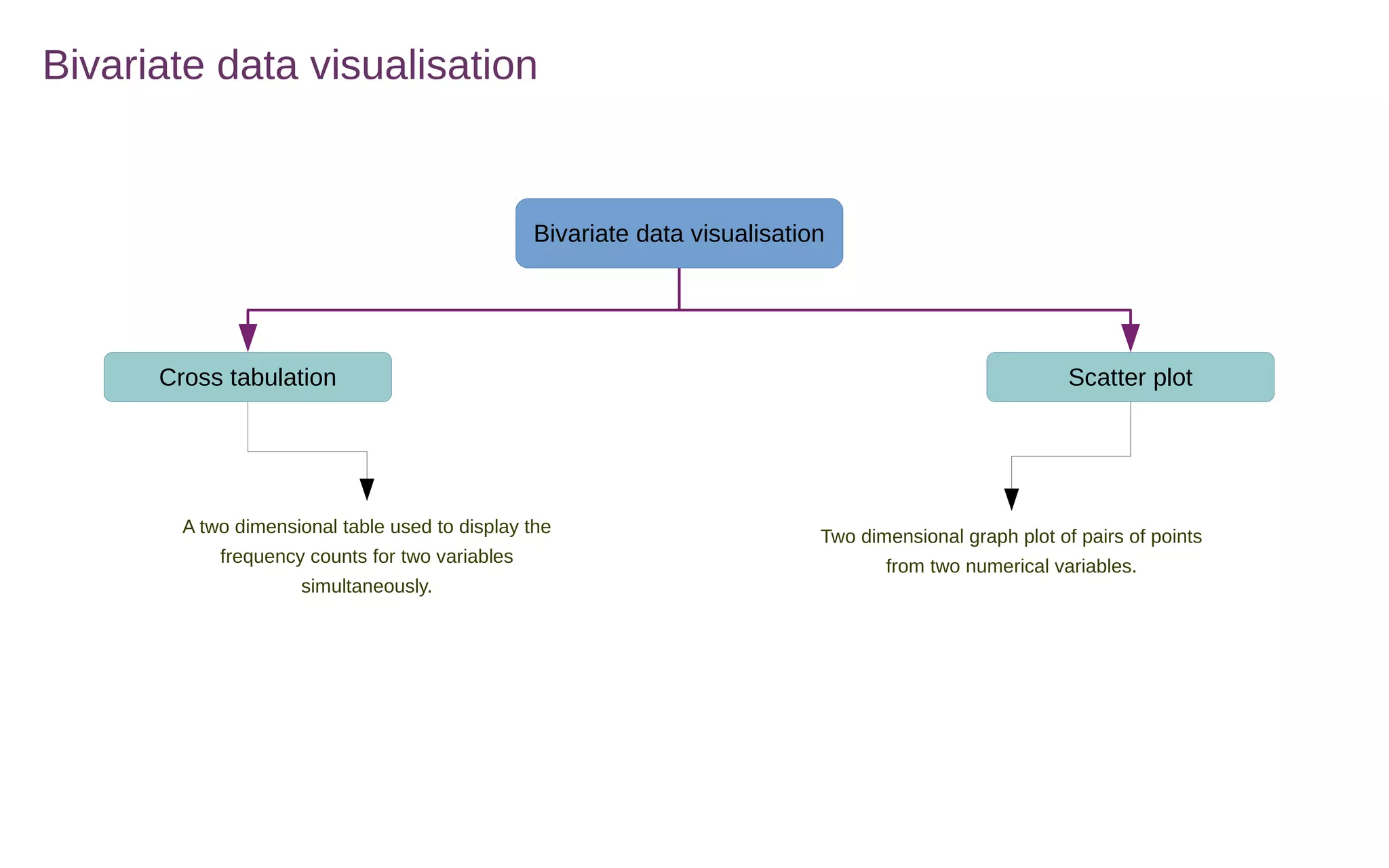
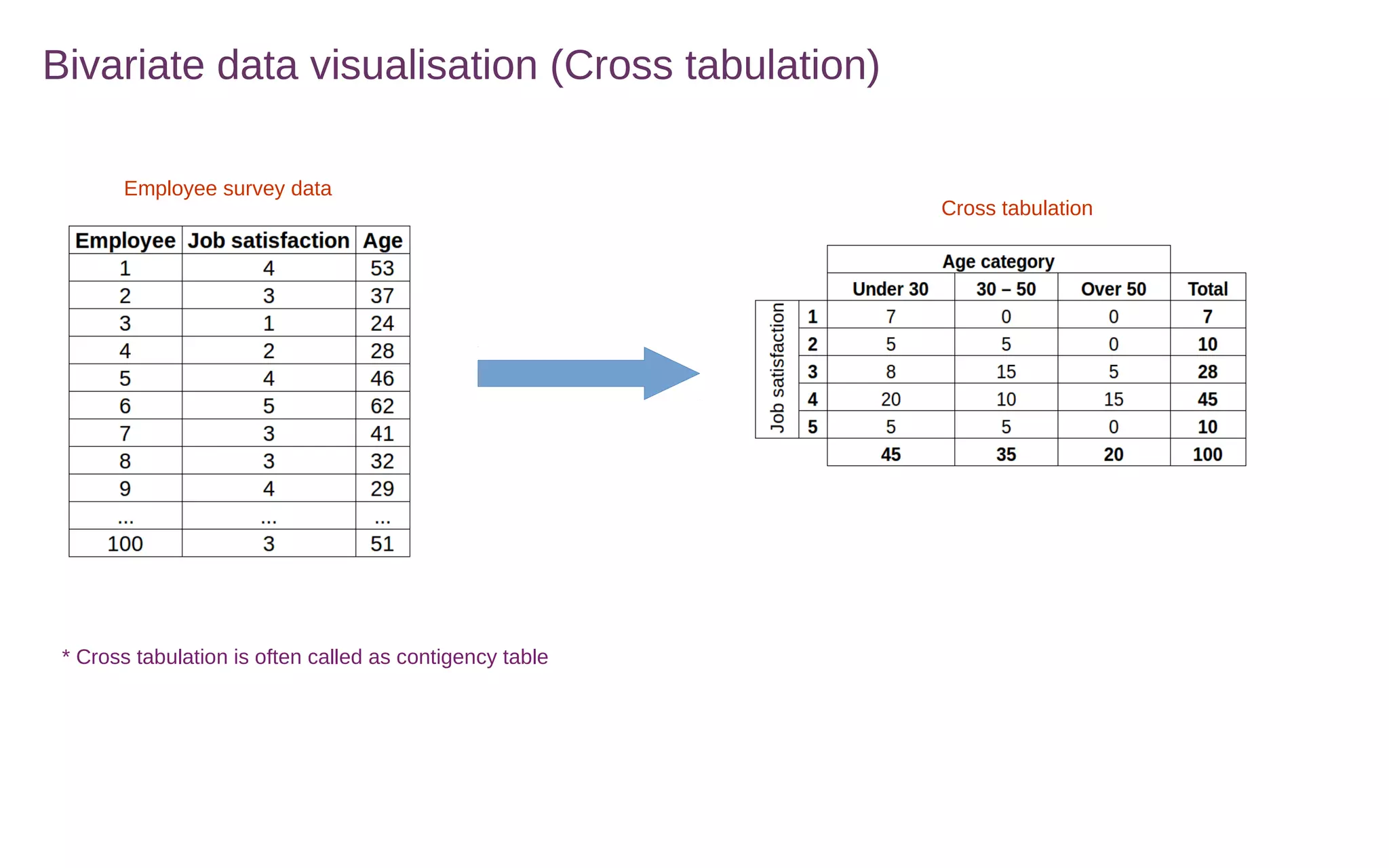
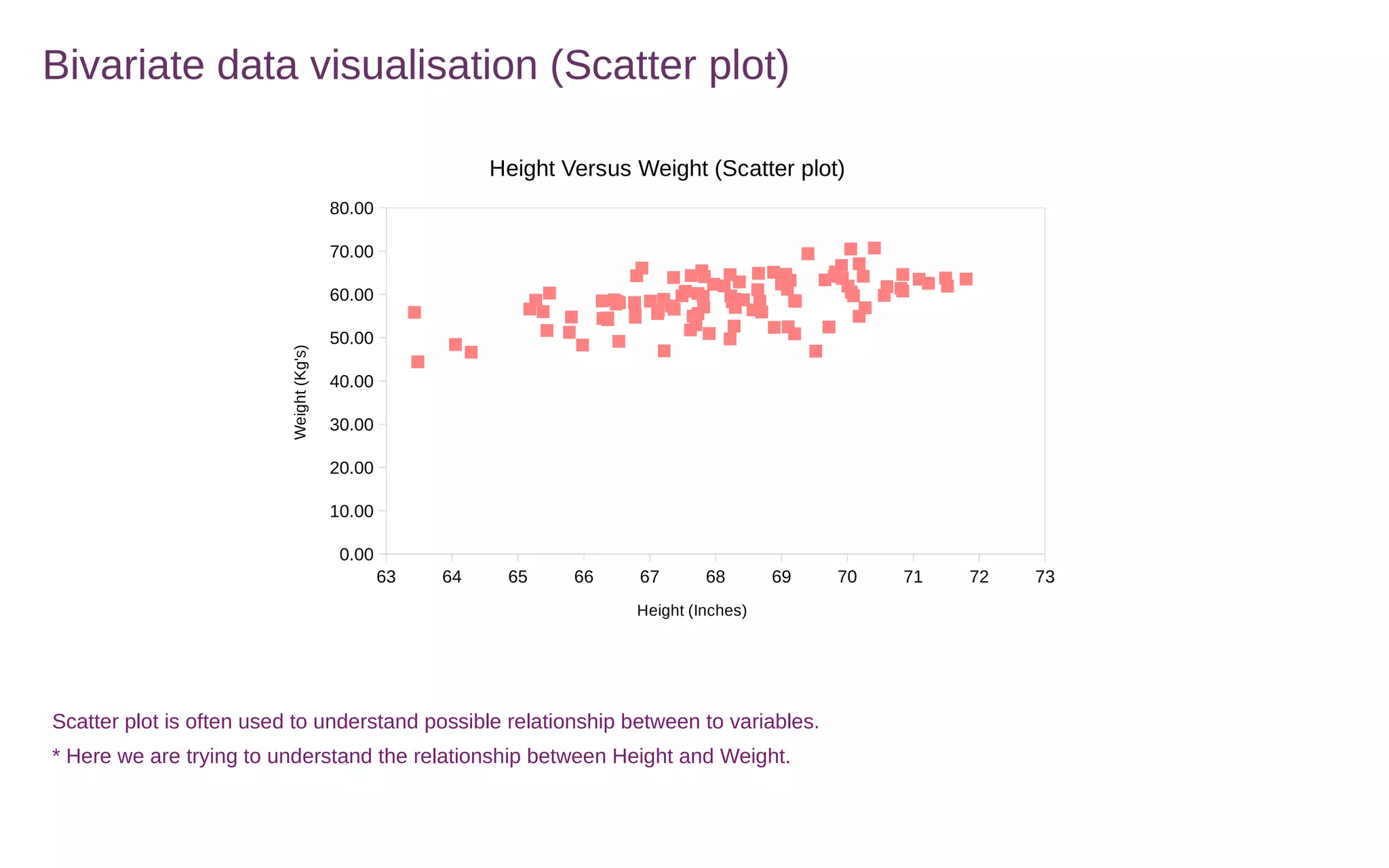
This document discusses various methods for summarizing and visualizing data, including frequency distributions, histograms, frequency polygons, ogives, stem-and-leaf plots, bar charts, pie charts, Pareto charts, cross tabulations, and scatter plots. Frequency distributions summarize grouped or ungrouped data using class intervals and frequencies. Histograms use rectangles to show frequencies of data in class intervals. Frequency polygons connect class midpoint dots instead of using rectangles. Ogives show cumulative frequencies. Stem-and-leaf plots separate digits into stems and leaves. Bar charts show categorical variable frequencies. Pie charts show parts of a whole. Pareto charts rank categories by cumulative proportion. Cross tabulations show frequencies of two variables. Scatter plots show relationships

1. Data summarisation & visualisation

2. Frequency distribution
Summarising data in a presentable format that is in the form of class intervals and frequencies
56 weeks of number of people visiting a store
(Ungrouped data)
56 weeks of number of people visiting a store
(Grouped data)
Class width = Range / Number of classes
Range = Max – Min
Range = 60 – 11 = 49
Number of classes we want = 5
Class width = (49/5) = 9.8
Round 9.8 = 10
* Rule of thumb is to create between 5
and 15 classes
Class interval, Class midpoint, Relative frequencies, Cumulative frequencies
for number of people visiting a store
Relative frequency = Individual class frequency / Total
frequency
Relative frequency = 7 / 56 = 0.13
Cumulative frequency is a running total of frequencies
through the classes

3. Univariate data visualisation
Univariate data visualisation
Numerical data Categorical data
Histogram Bar graph
Quantitative
data graphs
Qualitative
data graphs
Ogive Pareto chart
Frequency polygon Pie chart
Stem and Leaf plot
Quantitative data graphs are plotted along a
numerical scale
Qualitative data graphs are plotted using non-
numerical categories

4. Univariate numerical data visualisation (Histogram)
1. Series of continous rectangles represent the frequency of data in given class intervals.
2. X axis : With class mid points and Y axis: With the frequencies.
3. Quick glance at a histogram helps revealing which class intervals produce highest frequency.
* If the class intervals are unequal then the width of the rectangle or area of the rectangles can be used for relative comparison.

5. Univariate numerical data visualisation (Frequency polygon)
1. Is like histogram, however instead of using rectangles like a histogram each class frequency is plotted as a dot at the class midpoint
and the dots are connected by a series of line segments
2. X axis : With class mid points and Y axis: With the frequencies.

6. Univariate numerical data visualisation (Ogive)
1. Ogive is a cumulative frequency polygon
2. X axis :Always class end points and Y axis: With the cumulative frequencies.
* Generally used by decission makers to see the running totals

7. Univariate numerical data visualisation (Stem and Leaf Plot)
1. Constructed by separating the digits for each number of data into two groups a stem and a leaf.
2. Stem: Consists higher valued digits & Leaves: Contain lower values
56 weeks of number of people visiting a store
(Ungrouped data)
Stem & Leaf plot

8. Univariate categorical data visualisation (Bar chart)

9. Univariate categorical data visualisation (Pie chart)
13%
7%
25%
32%
24%
Total sales contribution "Product wise"
Product 1
Product 2
Product 3
Product 4
Product 5

10. Univariate categorical data visualisation (Pareto chart)
Product 4 Product 3 Product 5 Product 1 Product 2
0
50
100
150
200
250
300
350
400
450
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
32%
57%
81%
93%
100%
Sales (Pareto chart)
Product
Totalsales
Cumulativeproportion
Sort the data in the descending order and use cumulative proportion to plot pareto chart.
* Generally pareto chart are used in defect analysis that is types of defects that occur with a product and service.
* Most common types of defects ranked in order of occurence from left to right and accordingly control persons analyse pareto chart and
make the possible improvement from time to time.

11. Bivariate data visualisation
Bivariate data visualisation
Cross tabulation Scatter plot
A two dimensional table used to display the
frequency counts for two variables
simultaneously.
Two dimensional graph plot of pairs of points
from two numerical variables.

12. Bivariate data visualisation (Cross tabulation)
Employee survey data
Cross tabulation
* Cross tabulation is often called as contigency table

13. Bivariate data visualisation (Scatter plot)
63 64 65 66 67 68 69 70 71 72 73
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
80.00
Height Versus Weight (Scatter plot)
Height (Inches)
Weight(Kg's)
Scatter plot is often used to understand possible relationship between to variables.
* Here we are trying to understand the relationship between Height and Weight.