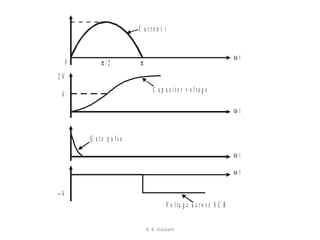
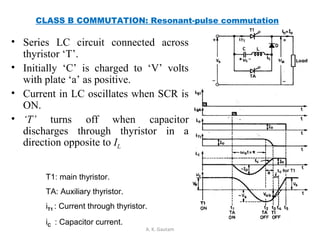
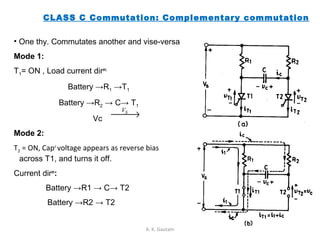
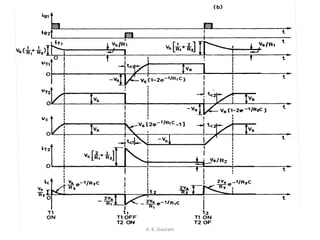
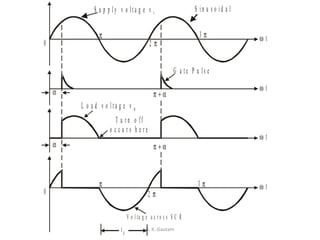
Thyristor commutation techniques can be natural or forced. Natural commutation occurs in AC circuits when the thyristor turns off as the AC voltage passes through zero. Forced commutation is used in DC circuits using methods like self, resonant pulse, complementary, and impulse commutation. Self commutation uses an underdamped LC circuit to create oscillating current that turns off the thyristor when current reaches zero. Resonant pulse commutation uses an auxiliary thyristor to discharge the capacitor and create reverse voltage across the main thyristor. Complementary commutation uses one thyristor to turn off the other in alternating fashion. Impulse commutation uses an inductor to create oscillating current for

1. Thyristor commutation
Techniques
A. K. Gautam
By:
Aniruddha K. Gautam
AKGEC, Ghaziabad

2. Methods of Commutations
• Natural Commutations
• Forced commutations
A. K. Gautam

3. ~
T
+
−
v ov s
R↑ ↑
Natural Commutation
•Occurs in AC circuits
•Natural Commutation of Thyristors takes place in
•AC voltage controllers.
•Phase controlled rectifiers.
•Cyclo-converters
A. K. Gautam

4. A. K. Gautam
ω t
ω t
ω t
ω t
S u p p l y v o l t a g e v s
S i n u s o i d a l
V o l ta g e a c r o s s S C R
L o a d v o l t a g e v o
T u r n o ff
o c c u r s h e r e
0
0
π
π
2 π
2 π
3 π
3 π
α
t c
G a t e P u l s e
π + α
α π + α

5. Forced Commutation
• Applied to
• dc circuits
• Choppers
• Inverters.
• Commutation achieved by reverse biasing the
SCR or by reducing the SCR current below
holding current value.
• Commutating elements such as inductance and
capacitance are used for commutation purpose.
A. K. Gautam

6. Methods of Forced Commutation
• Self commutation.
• Resonant pulse commutation.
• Complementary commutation.
• Impulse commutation.
• External pulse commutation.
• Line Commutation.
A. K. Gautam

7. CLASS A COMMUTATION: LOAD COMMUTATION
OR
(SELF COMM.)
• When R is low : L & C connects in series with R
• When R is high : C connects in Parallel with R
• Useful for dc Circuits.
•System should be under damped.
•When energized from a dc source, current must have
a natural tendency to decay to zero.
•Change in direction of current make the thyristor
turn- off.
•Oscillating current flows.
•SCR is turned off when current is zero.
A. K. Gautam

8. Self commutation
•Circuit is under damped by including suitable values
of L & C in series with load.
•Oscillating current flows.
•SCR is turned off when current is zero.
A. K. Gautam
V
R L V ( 0 )c
C
T i
L o a d
+ -

9. Expression for Current
A. K. Gautam
V
S
R S L
1
C S
V C ( 0 )
S
C
T I ( S ) + +- -
Fig. shows a transformed network
( )
( )
( )
( )
( )
2
2
1
0
1
0
1
0C
C
CCS V V
SI S
RC
V V
SI S
R SL
CS
C
S S LC
V V
R
LC S S
L LC
 − 
=
+ +

 − 
=
+
− 
=
 
+ +
+

( )
( )
( )
( )( )
2
2 2
2
0
1
0
1
2 2
C
C
V V
LI S
R
S S
L LC
V V
LI S
R R R
S S
L LC L L
−
=
+ +
−
=
   
+ + + − ÷  ÷
   

10. A. K. Gautam
( )
( )( )
( )
( )( )
2 2 2
2 2
2
0
1
2 2
Where,
0 1
, ,
2 2
C
C
V V
ALI S
SR R
S
L LC L
V V R R
A
L L LC L
δ ω
δ ω
−
= =
+ +     + + − ÷  ÷
     
−  
= = = − ÷
 
( )
( )
( )
2 2
is called the natural frequency
Taking inverse Laplace transforms
sint
A
I S
S
A
i t e tδ
ω
ω
ω δ ω
ω
ω
−
=
+ +
=

11. A. K. Gautam
( )
( )
( )( )
2
Expression for current
0
sin
Peak value of current
0
R
t
C L
C
V V
i t e t
L
V V
L
ω
ω
ω
−
∴
−
=
−
=
Expression For Voltage Across Capacitor At The Time Of
Turn Off
V
R L V ( 0 )c
C
T i
L o a d
+ -

12. A. K. Gautam
( )
( )
( )
Applying KVL to figure
Substituting for i,
sin sin
c R L
c
t t
c
v t V v V
di
v t V iR L
dt
A d A
v t V R e t L e t
dt
δ δ
ω ω
ω ω
− −
= − −
= − −
 
= − −  ÷
 
( ) ( )
( ) [ ]
( )
( )
sin cos sin
sin cos sin
sin cos sin
2
sin cos
2
t t t
c
t
c
t
c
t
c
A A
v t V R e t L e t e t
A
v t V e R t L t L t
A R
v t V e R t L t L t
L
A R
v t V e t L t
δ δ δ
δ
δ
δ
ω ω ω δ ω
ω ω
ω ω ω δ ω
ω
ω ω ω ω
ω
ω ω ω
ω
− − −
−
−
−
= − − −
= − + −
 
= − + −  
 
= − +  

13. A. K. Gautam
( )
( )( )
( )
( )( )
Substituting for A,
0
sin cos
2
0
sin cos
2
SCR turns off when current goes to zero.
i.e., at
C t
c
C t
c
V V R
v t V e t L t
L
V V R
v t V e t t
L
t
δ
δ
ω ω ω
ω
ω ω ω
ω
ω π
−
−
−  
= − +  
−  
= − +  
=
( )
( )( ) ( )
( ) ( )
( ) ( ) 2
Therefore at turn off
0
0 cos
0
0
C
c
c C
R
L
c C
V V
v t V e
v t V V V e
v t V V V e
δ π
ω
δ π
ω
π
ω
ω π
ω
−
−
−
−
= − +
 = + − 
 ∴ = + − 

14. A. K. Gautam
( )
( )
2
For effective commutation
the circuit should be under damped.
1
That is
2
With R = 0, and the capacitor initially uncharged
that is 0 0
sin
Note:
C
R
L LC
V
V t
i t
L LCω
 
< ÷
 
=
=
( )
1
But
sin sin
and capacitor voltage at turn off is equal to 2V
Fig. shows the waveforms for the above conditions.
Once the SCR turns off voltage across it is
negative voltage.
LC
V t C t
i t LC V
L LLC LC
ω =
∴ = =

15. A. K. Gautam
C u r r e n t i
C a p a c i t o r v o l t a g e
G a t e p u l s e
V o l ta g e a c r o s s S C R
0 ππ / 2
ω t
ω t
ω t
ω t
V
− V
2 V

16. CLASS B COMMUTATION: Resonant-pulse commutation
T1: main thyristor.
TA: Auxiliary thyristor.
iT1 : Current through thyristor.
iC : Capacitor current.
A. K. Gautam
• Series LC circuit connected across
thyristor ‘T’.
• Initially ‘C’ is charged to ‘V’ volts
with plate ‘a’ as positive.
• Current in LC oscillates when SCR is
ON.
• ‘T’ turns off when capacitor
discharges through thyristor in a
direction opposite to IL

17. Operations:
Mode 1:
• TA= OFF, T1= OFF
• Flow of current through C, current ic
starts flowing and C charges up to VS.
Mode 2:
• TA = OFF, T1= ON at t=0
• iT1 = iO
• When 0<t>t1
VC = VS
iC = 0
iO = IO
iT1 = iO
Mode 3:
TA = ON, T1= ON at t=t1
Current iC path : C→TA →L →CC S P O
C
i V Sin t I Sin t
L
ω ω=− =−
1
C S OV idt V Cos t
C
ω= =∫
Mode 4:
T= t2
+
TA= OFF , Vc= - Vs
Flow of resonant current: C→L →D →T1
As well as Ic increases which is opp. To
T1, iT1=Io-Ic, begin to decrease.
When Ic- Io, iT1=0, means T1= off
Mode 5:
T1= OFF at t = t3
Io flow through, C→L →D. Vc ↑ 0 → Vab
At t= t4 , Vc ↑0 → Vs
→
A. K. Gautam

18. 3 2( )o S o
C
I V Sin t t
L
ω= −
1
3 2
1
( )
( )
o
Io
Sin
t t Ip
ω −
=
−
p s
C
I V
L
=
4 3
ab
c
O
V
t t t C
I
= − =
3 2cos ( )ab oV Vs t tω= −
….(1)
….(2)
….(3)
….(4)
….(5)
Circuit turn=off time
Peak resonant current
A. K. Gautam

19. CLASS C Commutation: Complementary commutation
• One thy. Commutates another and vise-versa
Mode 1:
T1= ON , Load current dirn:
Battery →R1 →T1
Battery →R2 → C→ T1
Vc
Mode 2:
T2 = ON, Capr
voltage appears as reverse bias
across T1, and turns it off.
Current dirn
:
Battery →R1 → C→ T2
Battery →R2 → T2
SV
→
A. K. Gautam

20. 1 1
1
S
R
V
I I
R
≅ = 2
2
S
o R
V
I I
R
≅ =
When T1=ON at t = 0
or
1 2
1 1
1 1 ( )T C S R RI i i V= − = +
VC changes from 0→VS
2
( )
2
t
R CS
C
V
i e
R
−
=
2
( )
(1 )
t
R C
C SV V e
−
= −
When t= t+
So that VT1 =Vc(t)
After transient condition, Vc =VT2= VS , iC=0, 1
1
S
T
V
i
R
=
When t= t1
T2=ON, Vc (across T1) reverse and T1=OFF, VT2=0
A. K. Gautam

21. 1T SV V= −
1
2 S
C
V
i
R
= −
1 2
2 1
2 ( )T S R RI V= +, ,
• Applying KVL law:
1
1
C C SR i i dt V
C
+ =∫
• Laplace transformation:
1
( )1
( ) C S S
C
I S CV V
R I S
C S S S
 
+ − = 
 
• After taking inverse transformation
1( )
1
2
( )
t
R CS
C
V
i t e
R
−
=
Ci = opposite direction , So that 1( )
1
2
( )
t
R CS
C
V
i t e
R
−
=
• Again,
0
1
t
C S CV V i dt
C
= + ∫ =
1
( )
1
21 t
R CS
C S
V
V V e
C R
−  
= + −  ÷
  
∴
A. K. Gautam








−=






−
12 2CR
t
sc eVV

22. 2 1
1 2
1
1
( )
2
S R R
S
T
V
T V
i
R
i
+
=
→
When T=t2 transient condition are over now
VT1=Vs, ic=0, Vc=-Vs, VT2=Vs/R2, iT1=0
When T=t3
T1= ON, T2= commutated
iT2=0, VT2 =-Vs, VT1 =0, ic=2Vs/R2 iT1= 1 2
2 1
( )S R RV +
1
1
( )
1 0 1 2
tc
R C
T SV V e
−
 = = −
 
1 1 ln(2)Ct R C=
2 2 ln(2)Ct R C=
Turn of T2 at t1, capacitor voltage Vs suddenly appears as reverse biased across T1 to
turn it off.
Turn off time for T1 and T2
A. K. Gautam

23. A. K. Gautam

24. CLASS D COMMUTATION: Impulse Commutation
In such type of commutation circuit , a main thyristor, a auxiliary thy.,and an inductor
is used.
Mode 1:
T1-ON , io flows through Battery →T1 →load
Capacitor discharge dirn
, T1 →D →L, Capacitor
charged with opp. Polarity, which is not allowed due
to diode.
sin sinC S O P O
C
i V t I t
L
ω ω= =
1T C Oi i I= + (due to initial condition)
1T O P Oi I I Sin tω= +
1
O
LC
ω
 
= ÷
 
A. K. Gautam

25. Ip= Peak capacitor voltage
0
1
offt
L off
C L
i t
V i dt
C C
= =∫ L off
C
i t
C
V
=
Q P S
C
I V
L
=
m 1I ( )P axI throughT< mIS ax
C
V
L
<
2
2
mI ax
V C
L >
, , ,
Mode: 2
,
TA-ON, T1-off, C discharges through TA →T1, when this current= iO →T1-off
At t=t1
TA-ON, VT1= -VS, iT1=0
Now load current will flow through, C →TA
VC charges through –Vs to Vs
This method is called voltage commutation, due to T1 turns off due to reverse
voltage application A. K. Gautam

26. A. K. Gautam
External Pulse
Commutation (Class E Commutation)
V S V A U X
L
C
T 1 T 3T 2
R L
2 V A U X
+
−
•
•This Method of commutation used a pulse obtain from a source external to the main
circuit or obtain from a pulse forming network fed by an auxiliary voltage source.
• The pulse is used to apply a reverse bias and turn off the thyristor.
• Vaux Auxiliary voltage source
• L, C Oscillatory circuit to general a pulse.
•

27. Mode -1
• T1 T3– ON, VS – Used to supply the current through load.
• A current pulse flows having a peak value Vaux √C/L from V1 T3 L
C to charge up to 2VAUX
• When C is fully charged, Charging current tends to 0 , and T3 turns off.
Mode -1
• T2 ON ,
• Capacitor voltage appears as reverse bias across T1and turns it off.
• Capacitor C discharge through load.
A. K. Gautam

28. A. K. Gautam
• T1 is conducting & RL is connected across supply.
• T3 is fired & ‘C’ is charged to 2VAUX with upper plate
positive.
• T3 is self commutated.
• To turn off T1, T2 is fired.
• T2 ON results in a reverse voltage VS – 2VAUX
appearing across T1