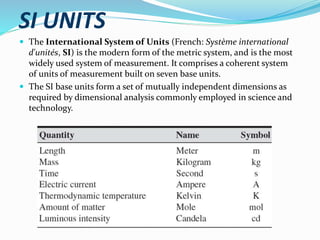
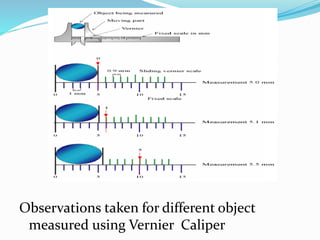
This document discusses physical measurement and errors in measurement. It defines key terms like measurement, units, observations, and least count. It describes the International System of Units (SI) as the modern metric system. It also discusses different types of errors like absolute error and relative error. Systematic errors can be corrected while random errors are reduced by taking multiple measurements. Accuracy refers to systematic errors while precision describes random errors. The document outlines methods to calculate propagation of errors and statistical treatment of error values.

1. MADE BY :
OJASVINI AHLUWALIA AND NIKHIL
NARMETA
BIO-TECH(Ist YEAR)

2. PHYSICAL MEASUREMENT
 Measurement is the process of obtaining the magnitude of a
quantity relative to an agreed standard.
 Measurement of any quantity involves comparison with some
precisely defined unit value of the quantity which is defined as
Unit of Measurement.

3. SI UNITS
 The International System of Units (French: Système international
d'unités, SI) is the modern form of the metric system, and is the most
widely used system of measurement. It comprises a coherent system
of units of measurement built on seven base units.
 The SI base units form a set of mutually independent dimensions as
required by dimensional analysis commonly employed in science and
technology.

4. PHYSICAL OBSERVATIONS
 Observation consists of receiving knowledge of the outside
world through our senses, or recording information using
scientific tools and instruments. Any data recorded during
an experiment can be called an observation.
 The subject of physics establishes the facts on the basis of
experimental observations, which involve direct or indirect
measurement of various physical quantities.

5. Observations taken for different object
measured using Vernier Caliper

6. LEAST COUNT
 The smallest value that can be measured by the measuring instrument is called
its least count. .
 The least count is related to the precision of an instrument; an instrument that
can measure smaller changes in a value relative to another instrument, has a
smaller "least count" value and so is more precise.
 For example, a sundial may only have scale marks representing the hours of
daylight; it would have a least count of one hour. A stopwatch used to time a race
might resolve down to a hundredth of a second, its least count. The stopwatch is
more precise at measuring time intervals than the sundial because it has more
"counts" (scale intervals) in each hour of elapsed time. Least count of an
instrument is one of the very important tools in order to get accurate readings of
instruments like vernier caliper and screw gauge used in various experiments.
 SUNDIAL STOPWATCH

7. ERROR
 In science, the word “error” means the “uncertainty” which
accompanies every measurement. No measurement of any sort
is complete without a consideration of this inherent error
 The uncertainty is the result of :
i. theoretical prediction measurement
ii. by a sophisticated instrument
iii. average evaluated from a very large number of measurement
 A discrepancy on the other hand is the difference between
two measured values of a physical quantity.

8. TYPES OF ERRORS IN MEASUREMENT
 Absolute Error is the difference between the measured value and the
actual value.
For example, if you know a length is 3.535 m + 0.004 m, then 0.004 m is an
absolute error. Absolute error is positive.
 Relative Error is the ratio of the absolute error of the measurement to
the accepted measurement. It is considered to be a measure of accuracy.
 Percentage Error : error in measurement may also be expressed as
a percent of error. The percent of error is found by multiplying the relative
error by 100%.

9. ERROR
SYSTEMATIC ERROR RANDOM ERROR
Failure to calibrate or
check zero of instrument
Lag time and hysteresis
External factor
Parallax error
Physical variations
External factor

10. SYSTEMATIC ERRORS
Systematic errors are due to identified causes and can, in principle, be
eliminated. Errors of this type result in measured values that are
consistently too high or consistently too low.
 As opposed to random errors, systematic errors are easier to correct.
 Sometime the measuring instrument itself is faulty, which leads to a
systematic error. For example, if your stopwatch shows 100 seconds for an
actual time of 99 seconds, everything you measure with this stopwatch will be
dilated, and a systematic error is induced in your measurements. In this case,
the systematic error is proportional to the measurement.

11. SOURCES OF SYSTEMATIC ERROR
 Failure to calibrate or check zero of instrument - Whenever possible, the
calibration of an instrument should be checked before taking data. If a
calibration standard is not available, the accuracy of the instrument should be
checked by comparing with another instrument that is at least as precise, or by
consulting the technical data provided by the manufacturer. When making a
measurement with a micrometer, electronic balance, or an electrical meter,
always check the zero reading first.
 Lag time and hysteresis - Some measuring devices require time to reach
equilibrium, and taking a measurement before the instrument is stable will
result in a measurement that is generally too low. The most common
example is taking temperature readings with a thermometer that has not
reached thermal equilibrium with its environment. A similar effect is hysteresis
where the instrument readings lag behind and appear to have a "memory"
effect as data are taken sequentially moving up or down through a range of
values. Hysteresis is most commonly associated with materials that become
magnetized when a changing magnetic field is applied.
 External factor: Conditions like temperature , pressure , mechanical
vibrations may have a considerable effect on a measurement . They may effect
the calibration of the instrument or its quality.

12. RANDOM ERRORS
 Also known as Chance errors
 Random errors are errors in measurement that lead to
measurable values being inconsistent when repeated measures
of a constant attribute or quantity are taken.
 To minimize such errors large number of observations and
their arithmetic mean is evaluated.
 Statistical methods are used for dealing with random or chance
errors

13. TYPES OF RANDOM ERRORS
 A Parallax error can occur whenever there is some distance between
the measuring scale and the indicator used to obtain a measurement. If the
observer's eye is not squarely aligned with the pointer and scale, the
reading may be too high or low (some analog meters have mirrors to help
with this alignment).
 Physical variations - It is always wise to obtain multiple measurements
over the entire range being investigated. Doing so often reveals variations
that might otherwise go undetected. If desired, these variations may be
cause for closer examination, or they may be combined to find an average
value.

14. PRECISION VS ACCURACY
 Precision is a description of random errors, a measure of statistical
variability. Precision is the degree to which several measurements
provide answers very close to each other. It is an indicator of the scatter
in the data. The lesser the scatter, higher the precision.
 Accuracy is a description of systematic errors, a measure of statistical
bias. Accuracy describes the nearness of a measurement to the
standard or true value, i.e., a highly accurate measuring device will
provide measurements very close to the standard, true or known values

15. PROPOGATION OF ERRORS
Error propagation is the process of determining the
uncertainty of an answer obtained from a calculation.
The maximum possible error in resultant quantity can
be computed as follows:
Addition or Subtraction:

16. Multiplication or Division:
 Exponential: If we have a measured physical quantity
and another quantity defined as,
then relative error n C is n times the relative error in A.
If then
aaA 
n
AC 
n
AC 
a
a
n
c
c 



17. Trigonometric Functions : If a physical quantity is expressed as
trigonometric functions, then error will be of function and not of the
measured angle.
For example:
i. If the physical quantity is expressed as Z= , then we have
ii. If the physical quantity is expressed as Z= , then we have on
similar lines
iii. If the physical quantity is expressed as Z= , then we have on
similar lines
tan







2sin
2
cossin2
2
tan
sec
sec
2
2









Z
Z
Z
Z
Z
sin


tan



Z
Z
cos


cot



Z
Z

18. STATISTICAL TREATMENT OF ERRORS
 The arithmetic mean of N numbers of measured values that are reliable will be
given as :
 The precision with which a physical quantity is measured depends inversely
upon deviation.
 The deviation of the individual measurement from the mean value is defined as
 The standard deviation is defined as the square root of mean squared deviation
 The standard error now can be denoted as :


n
i
iX
n
X
1
1


n
i
i
n 1
1

 
  11
1
2
1
2




  
nn
n
i
i
n
i
XXi 

n
m

 