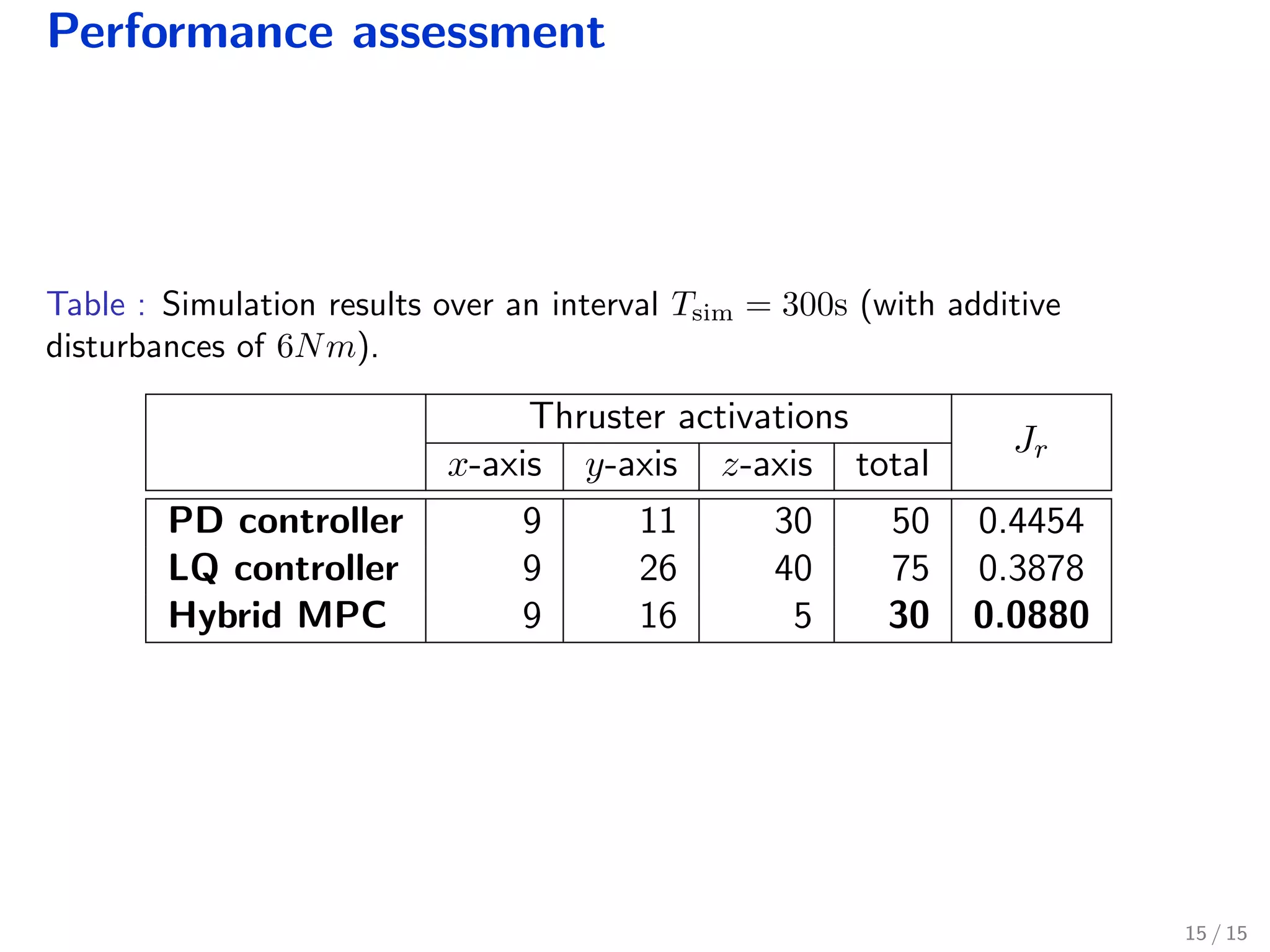
This document describes a hybrid model predictive control approach for attitude control of spacecraft using impulsive thrusters. The approach models the spacecraft dynamics and minimum impulse effects of the thrusters. It formulates the control problem as minimizing a cost function over future inputs while satisfying the hybrid dynamics and constraints, such as a limit on total thruster actuations. Simulations show the hybrid MPC achieves higher pointing accuracy, lower thruster usage, and better disturbance rejection compared to traditional PD and LQR controllers.

1. Hybrid MPC for Attitude Control of Spacecraft with
Impulsive Thrusters
P. Sopasakisa, D. Bernardinia,c, H. Strauchb,
S. Bennanid and A. Bemporada,c
a Institute for Advanced Studies Lucca,
b Airbus DS, c ODYS Srl
d European Space Agency
July 14, 2015

2. Control objectives
Operate in barbecue mode with ωx = 5 deg · s−1,
Achieve high pointing accuracy using impulsive thrusters
Low actuation count
Reasonable computational complexity
1 / 15

3. I. Attitude Modelling

4. Reference frame
Body-Fixed Frame:
2 / 15

5. Nonlinear dynamical model
Notation: ˜Θx, ˜Ψx: pitch and yaw error angles, ωi: angular velocity about
i-axis, ωn = (1 − Jxx/Jyy)ωx.1
d
dt






˜Θx
˜Ψx
ωx
ωy
ωz






=






0 ωx 0 1 0
−ωx 0 0 0 1
0 0 0 0 0
0 0 0 0 ωn
0 0 0 −ωn 0












˜Θx
˜Ψx
ωx
ωy
ωz






+
+






0 0 0
0 0 0
J−1
xx 0 0
0 J−1
yy 0
0 0 J−1
zz








τx
τy
τz


1
A. Kater, “Attitude Control of Upper Stage Launcher During Long Coasting Period,” Master’s thesis, Lehrstuhk fur
Automatisierungs und Regelungstechnik, Christian-Albrechts-University Kiel, Germany, 2013.
3 / 15

6. Linear Dynamical Model
Assumption: The spin rate equilibrates very fast, i.e., ωx(t) ωr
x.
Model is now written in two parts - the spin model2:
˙ωx = J−1
xx τx
and the nutation/precession model:
d
dt




˜Θx
˜Ψx
ωy
ωz



 =




ωr
x 1
−ωr
x 1
ωr
n
−ωr
n








˜Θx
˜Ψx
ωy
ωz



 +



J−1
yy
J−1
zz




τy
τz
2
The spin rate ωx is controlled with a simple but efficient P-controller.
4 / 15

7. Linear Dynamical Model
We introduce the state variable
x(t) = ˜Θx(t) ˜Ψx(t) ωy(t) ωz(t) ,
and the input vector
u(t) = τy(t) τz(t) ,
the nutation/precession model, after discretisation, is written concisely as
x(k + 1) = Ax(k) + Bu(k).
5 / 15

8. II. Impulsive Thrusters

9. Minimum impulse effect
Minimum impulse effect: thrusters cannot produce arbitrarily small
torques, thus uk is constrained in
U = [−umax, −umin] ∪ {0} ∪ [umin, umax]
We introduce the binary vectors δ− and δ+ so that3
δ−
(k) = [u(k) ≤ −umin],
δ+
(k) = [u(k) ≥ umin],
and the auxiliary variable ηk defined as4
ηi(k) = [δ−
i (k) ∨ δ+
i (k)] · ui(k)
3
Symbols ≤ and ≥ are element-wise comparison operators.
4
Here ηi(k) stands for the i-th component of vector η(k) at time k.
6 / 15

10. Minimum impulse effect
To detect thruster actuation we use the variable
v(k) = [δ−
(k) ∨ δ+
(k)]
and we recast the system dynamics as
z(k + 1) = Az(k) + Bη(k) + f,
γ(k + 1) = γ(k) + [ 1 1 ] v(k),
where γ(k) is the total actuation count up to time k on which we impose:
γ(k) ≤ γmax.
7 / 15

11. III. Hybrid MPC

12. Penalty function
For a sequence of control actions πN = {u(k), v(k), η(k), δ±(k)}N−1
k=0 we
define the total penalty function with horizon N as
V (πN ; x0, γ0) VN (x(N), γ(N)) +
N−1
k=0
(x(k), z(k)),
where is the stage cost
(x, z) Qx p
Penalises the
pointing inaccuracy
+ Rz p
and VN is the terminal cost,
VN (x(N), γ(N)) QN x(N) p + ρ(γ(N) − γ0)
Penalises the tot.
actuation count
along the horizon
.
8 / 15

13. Hybrid MPC - problem formulation
MPC problem formulation:
min
πN
V (πN ; x0, γ0)
s.t. x(0) = x0, γ(0) = γ0,
Hybrid dynamics, for k ∈ N[0,Nu−1],
δ±
(k) = 0, for k ∈ N[Nu,N−1],
9 / 15

14. IV. Simulations

15. Barbecue mode
2 4 6 8 10 12 14 16 18 20
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
time [s]
Rollrateerror[deg]
Absolute value of tracking error on ω
x
Figure : ωx converges fast to its set-point.
10 / 15

16. Pointing Accuracy
−4 −3 −2 −1 0 1 2
−6
−5
−4
−3
−2
−1
0
1
2
pitch error [deg]
yawerror[deg]
Tracking error on pitch and yaw
PD
LQ
HMPC
Figure : HMPC achieves higher pointing accuracy compared to optimally tuned
PD and LQR controllers (which do not account for the MI effect).
11 / 15

17. Actuation Count
50 100 150 200 250 300
−200
−100
0
100
200
LQRTorque[Nm]
50 100 150 200 250 300
−200
−100
0
100
200
PDTorque[Nm]
50 100 150 200 250 300
−4000
−2000
0
2000
HMPCTorque[Nm]
Time [s]
50 100 150 200 250 300
0
200
400
600
LQRTorque[Nm]
50 100 150 200 250 300
−200
−100
0
100
200
PDTorque[Nm]
50 100 150 200 250 300
−5000
0
5000
HMPCTorque[Nm]
Time [s]
Figure : HMPC achieves a significantly lower actuation count. Left: ωy, Right:
ωz.
12 / 15

18. ...with additive disturbances
−12 −10 −8 −6 −4 −2 0 2 4 6
−4
−2
0
2
4
6
8
10
12
14
pitch error [deg]
yawerror[deg]
Tracking error on pitch and yaw
Tsim
=500
PD
LQ
HMPC
Figure : Simulations in presence of a constant additive disturbance on uk of
6Nm.
13 / 15

19. Performance assessment
Performance indicators: (i) actuation count on axes y and z, (ii) total
actuation count, (iii) total squared deviation
Jr =
Tsim
k=0
˜Θ2
x(k) + ˜Ψ2
x(k) .
Table : Simulation results over an interval Tsim = 300s (nominal conditions).
Thruster activations
Jr
x-axis y-axis z-axis total
PD controller 9 7 34 50 0.4741
LQ controller 9 21 36 66 0.3858
Hybrid MPC 9 4 5 18 0.0811
14 / 15

20. Performance assessment
Table : Simulation results over an interval Tsim = 300s (with additive
disturbances of 6Nm).
Thruster activations
Jr
x-axis y-axis z-axis total
PD controller 9 11 30 50 0.4454
LQ controller 9 26 40 75 0.3878
Hybrid MPC 9 16 5 30 0.0880
15 / 15

21. Thank you for your attention