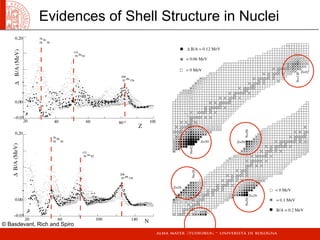
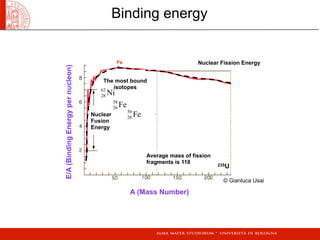
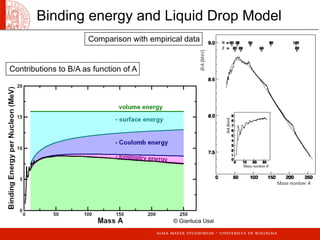
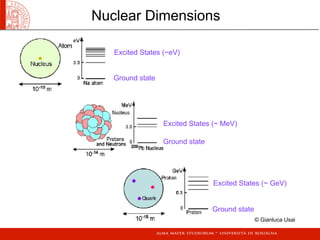
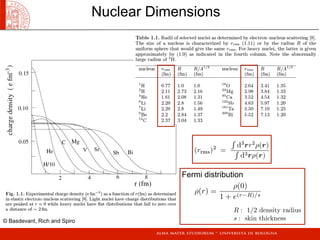
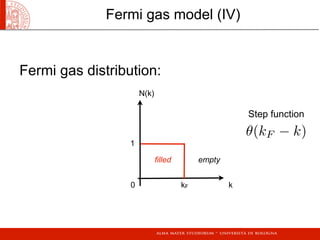
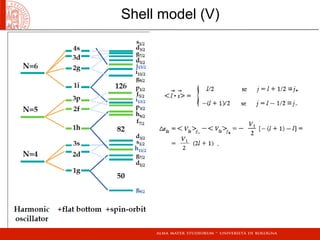
The document provides an introduction to basic concepts in nuclear physics, including: - Binding energy and the liquid drop model, which describes the saturation of nuclear forces. - Nuclear dimensions and the different energy scales involved. - The Fermi gas model, which treats nuclei as two fermion gases and can provide constants for binding energy formulas. - The shell model, which incorporates a mean field potential and spin-orbit potential to reproduce shell structure in nuclei. 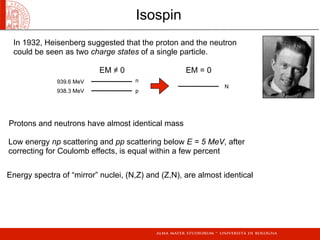- Isospin, which treats protons and neutrons as states of a single particle to explain similarities in their behavior.

1. Basic Concepts in
Nuclear Physics
Paolo Finelli

2. Literature/Bibliography
Some useful texts are available at the Library:
Wong,
Nuclear Physics
Krane,
Introductory Nuclear Physics
Basdevant, Rich and Spiro,
Fundamentals in Nuclear Physics
Bertulani,
Nuclear Physics in a Nutshell

3. Introduction
Purpose of these introductory notes is recollecting few basic notions of
Nuclear Physics. For more details, the reader is referred to the literature.
Binding energy and Liquid Drop Model
Nuclear dimensions
Saturation of nuclear forces
Fermi gas
Shell model
Isospin
Several arguments will not be covered but, of course, are extremely
important: pairing, deformations, single and collective excitations,
α decay, β decay, γ decay, fusion process, fission process,...

4. The Nuclear Landscape
The scope of nuclear physics is
Improve the knowledge of all nuclei
Understand the stellar nucleosynthesis
© Basdevant, Rich and Spiro

5. e−5
e−6
e−7
≥ e−4
Stellar Nucleosynthesis
Dynamical r-process calculation assuming an
expansion with an initial density of 0.029e4 g/cm3, an
initial temperature of 1.5 GK and an expansion
timescale of 0.83 s.
The r-process is responsible for the
origin of about half of the elements
heavier than iron that are found in
nature, including elements such as
gold or uranium. Shown is the result of
a model calculation for this process
that might occur in a supernova
explosion. Iron is bombarded with a
huge flux of neutrons and a sequence
of neutron captures and beta decays is
then creating heavy elements.
The evolution of the nuclear abundances. Each square is a nucleus. The colors indicate the
abundance of the nucleus:
©JINA

6. mN c2
= mAc2
− Zmec2
+
Z
i=1
Bi mAc2
− Zmec2
B = (Zmp + Nmn) c2
− mN c2
[Zmp + Nmn − (mA − Zme)] c2
B =
Zm( 1
H) + Nmn − m( A
X)
c2
Binding energy
Electrons Mass (~Z)
Atomic Mass Electrons Binding Energies
(negligible)
© Basdevant, Rich and Spiro

7. E/A(BindingEnergypernucleon)
A (Mass Number)
Average mass of fission
fragments is 118
Fe Nuclear Fission Energy
Nuclear
Fusion
Energy
235U
© Gianluca Usai
The most bound
isotopes
Binding energy

8. Binding energy and Liquid Drop Model
© Basdevant, Rich and Spiro
Volume term, proportional to R3 (or A): saturation
Surface term, proportional to R2 (or A2/3)
Coulomb term, proportional to Z2/A1/3
Pairing term, nucleon pairs
coupled to JΠ=0+ are favored
Asymmetry term, neutron-rich nuclei are favored

9. Binding energy and Liquid Drop Model
© Gianluca Usai
Contributions to B/A as function of A
Comparison with empirical data

10. Nuclear Dimensions
Ground state
Excited States (~eV)
© Gianluca Usai
Ground state
Ground state
Excited States (~ MeV)
Excited States (~ GeV)

11. Nuclear Dimensions: energy scales

12. ρ(r) =
ρ(0)
1 + e(r−R)/s
R : 1/2 density radius
s : skin thickness
Nuclear Dimensions
© Basdevant, Rich and Spiro
Fermi distribution

13. Nuclear forces saturation
An old (but still good) definition:
© E. Fermi, Nuclear Physics

14. Mean potential method: Fermi gas model
In this model, nuclei are considered to be composed of two fermion gases,
a neutron gas and a proton gas. The particles do not interact, but they are
confined in a sphere which has the dimension of the nucleus. The
interaction appear implicitly through the assumption that the nucleons are
confined in the sphere. If the liquid drop model is based on the saturation
of nuclear forces, on the other hand the Fermi model is based on the
quantum statistics effects.
The Fermi model could provide a way to calculate
the basic constants in the Bethe-Weizsäcker formula

15. H =
A
i=1
Ti ≡
A
i=1
−
2
2M
∇2
i
Hψ(r1,r2, . . .) = Eψ(r1,r2, . . .)
ψ(r1,r2, . . .) = φ1(r1)φ2(r2) . . .
−
2
2M
∇2
i φ(ri) = Eφ(ri)
E = E1 + E2 + E3 + . . . =
A
i=1
Ei
k2
i ≡ (k2
ix + k2
iy + k2
iz) =
2MEi
2
0
φi(r) ≡ φi(x, y, z) = N sin(kixx) sin(kiyy) sin(kizz)
d2
φi(x)
dx2
= −k2
ixφi(x)
Fermi gas model (I)
Hamiltonian
Wavefunction factorization
Boundary conditions
Separable equations
Gasiorowicz, p.58

16. φi(x) = B sin(kixx)
1 =
L
0
dx|φi(x)|2
= B2
L
0
dx sin2
(kixx) = B2 L
2
B =
2
L
φi(r) =
2
L
3/2
sin(kixx) sin(kiyy) sin(kizz)
kix =
π
L
n1i , kiy =
π
L
n2i , kiz =
π
L
n3i
(n1i, n2i, n3i = positive integers)
Ei =
2k2
i
2M
=
2
2M
(k2
ix + k2
iy + k2
iz)
Ei(n1i, n2i, n3i) =
2
π2
2ML2
(n2
1i + n2
2i + n2
3i)
Fermi gas model (II)
Solution
Normalization

17. ∆kx,y,z =
π
L
(n1,2,3 + 1 − n1,2,3) =
π
L
dn(k) =
1
8
4πk2
dk
1
(π/L)3
≡
Ω
(2π)3
dk
n(¯k) =
¯k
0
dn(k) =
Ω
(2π)3
4π
3
¯k3
A = 4
kF
0
dn(k) =
Ω
(2π)3
4
4π
3
k3
= Ω
2k3
F
3π2
ρ0 =
2k3
F
3π2
Ω ≡ L3
ρ0 = A/Ω
Fermi gas model (III)
Density of states
Number
of particles
Density
of particles
spin-isospin
Fermi momentum

18. θ(kF − k)
Fermi gas model (IV)
Fermi gas distribution:
N(k)
kkF
1
0
Step function
filled empty

19. ρ0 = 0.17 fm−3
kF = 1.36 fm−1
F =
2
k2
F
2M
= 38.35 MeV
T = 23 MeV
4dn(k)N(k) = 4
Ω
(2π)3
θ(kF − k)dk
T = Ω
2
π2
2
k2
2M
k2
dkθ(kF − k) = Ω
2k3
F
3π2
3
5
2
k2
F
2M
= A
3
5
F
(BE)vol = −bvolA (bvol = 15.56 MeV)
U = −15.56− T −39 MeV
Fermi gas model (V)
The fermi level is
the last level occupied

20. Evidences of Shell Structure in Nuclei
© Basdevant, Rich and Spiro

21. En = (n + 3/2)ω
H = Vls(r)l · s/2
l·s
2 = j(j+1)−l(l+1)−s(s+1)
2
= l/2 j = l + 1/2
= −(l + 1)/2 j = l − 1/2
Mean potential method: Shell model
The shell model, in its most simple
version, is composed of a mean
field potential (maybe a harmonic
oscillator) plus a spin-orbit
potential in order to reproduce the
empirical evidences of shell
structure in nuclei
© Basdevant, Rich and Spiro

22. Mean potential method: Shell model

23. Hi =
1
2m
p2
i +
1
2
Mω2
0r2
i − V0
p2
2M
+
1
2
Mω2
0r2
ψ(r) = (E + V0)ψ(r)
ψ(r) = Rnl(r)Ylm(θ, φ)
Rnl(r) = (−1)n
2
(l + 1/2)!
l + n + 1/2
n
rl
e−λr2
/2
1F1
−n, l +
3
2
, λr2
Shell model (I)
H =
A
i=1
Hi

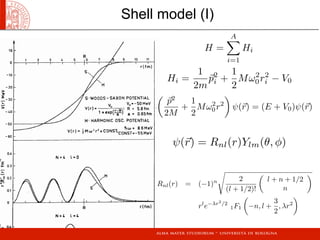
24. 1F1 (−n, µ + 1, z) =
Γ(n + 1)Γ(µ + 1)
Γ(n + µ + 1)
Lµ
n(z)
EN =
N +
3
2
ω0 N = 2n + l
d = 2
N
l=0
(2l + 1) = 2
[N/2]
n=0
(2(N − 2n) + 1) =
= 2(2N + 1)
N
2
+ 1
− 8
[N/2]
n=0
d = (N + 1)(N + 2)
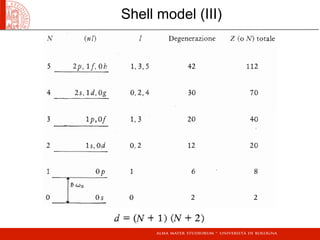
Shell model (II)
Degeneracy

25. Shell model (III)

26. Shell model (IV)

27. Shell model (V)

28. Shell model (V)

29. Isospin
In 1932, Heisenberg suggested that the proton and the neutron
could be seen as two charge states of a single particle.
939.6 MeV
938.3 MeV
EM ≠ 0 EM = 0
n
p
N
Protons and neutrons have almost identical mass
Low energy np scattering and pp scattering below E = 5 MeV, after
correcting for Coulomb effects, is equal within a few percent
Energy spectra of “mirror” nuclei, (N,Z) and (Z,N), are almost identical

30. ψN (r, σ, τ) =
ψp(r, σ, 1
2 ) proton
ψn(r, σ, −1
2 ) neutron
η1
2 , 1
2
= |π =
1
0
η1
2 ,− 1
2
= |ν =
0
1
Isospin is an internal variable that determines the nucleon state
One could introduce a (2d) vector space that is mathematical copy of the
usual spin space
proton state neutron state
Isospin (II)

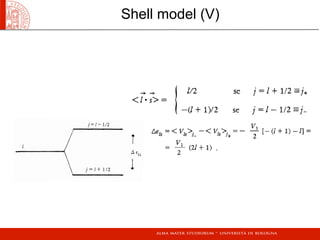
31. τ3|π = |π
τ3|ν = −|π
ψN = a|π + b|ν =
a
b
[ti, tj] = iijktk
Pp = 1+τ3
2 =
ˆQ
e
Pn = 1−τ3
2
τ1, τ2, τ3
ti =
1
2
τi
t+|ν = |π
t−|π = |ν
t+|π = 0
t−|ν = 0
t± = t1 ± it2
Isospin
eigenstates of the third component of isospin
In general
The isospin generators
Projectors Raising and lowering operators
Pauli matrices
neutron to
proton proton to
neutron
Fundamental representations

32. T = t1 + t2 T = 0, 1
T = 0 η0,0 = 1√
2
(π1ν2 − ν1π2)
T = 1



η1,1 = π1π2
η1,−1 = ν1ν2
η1,0 = 1√
2
(π1ν2 + π2ν1)
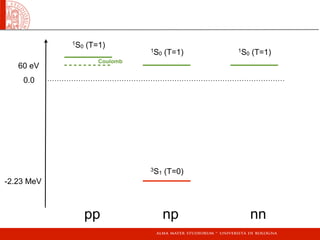
Isospin for 2 nucleons
|T = 1, Tz = 1 = |pp
|T = 1, Tz = −1 = |nn
1
√
2
[|T = 1, Tz = 0 + |T = 0, Tz = 0] = |pn
Proton-proton state
Neutron-neutron state
Proton-neutron state

33. Isospin for 2 nucleons
ψ(1, 2) = ψpp(r1, σ1, r2, σ2)η1,1 + ψnn(r1, σ1, r2, σ2)η1,−1 + ψa
np(r1, σ1, r2, σ2)η1,0 + ψs
np(r1, σ1, r2, σ2)η0,0
PT =0
=
1 − τ(1)
τ2
4
PT =1
ν=1 =
1 + τ
(1)
3
2
1 + τ
(2)
3
2
PT =1
ν=0 =
1
4
(1 + τ(1)
τ(2)
− 2τ
(1)
3 τ
(2)
3 )
η0,0η1,1
PT =1
ν=−1 =
1 − τ
(1)
3
2
1 − τ
(2)
3
2 η1,−1 η1,0
antisymmetric symmetric
Wavefunction

34. Ψ(r,s1,s2,t1,t2) = φ(r)fσ(s1,s2)fτ (t1,t2)
(−)L+S+T
= (−)
Symmetry for two nucleon states
the overall wavefunction must be antisymmetric
L=0, S=1 T=0 3S1
isospin singlet

35. Sistema di 2
nucleoni identici
(pp,nn)
Sistema di 2
nucleoni distinti
(pn)
ISOSPIN SPAZIO SPIN
Tz = ±1
Tz = 0
Funzione simmetrica
(tripletto T=1)
Funzione antisimmetrica
(singoletto T=0)
L dispari
L dispari
L pari
L dispari
ψ(x)
ψ(x)
ψ(x)
ψ(x)
antisimmetrica
antisimmetrica
simmetrica
simmetrica
S=1
simmetrica
(no onda S)
S=0
ψ(σ)
ψ(σ) antisimmetrica
1
S0
L pari
L pari
ψ(x) simmetrica
ψ(x) antisimmetrica
S=1
S=1
simmetricaψ(σ)
simmetricaψ(σ)
S=0
S=0
ψ(σ) antisimmetrica
ψ(σ) antisimmetrica
(no onda S)
1
S0
(no onda S)
3
S1
Tz = 0
Funzione simmetrica
(tripletto T=1)

36. pp np nn
0.0
60 eV
-2.23 MeV
3S1 (T=0)
1S0 (T=1)1S0 (T=1)
1S0 (T=1)
Coulomb

37. Additional slides

38. ...many open questions

39. v(r − r
) = −v0δ(r − r
)
V (r) =
dr
v(r − r
)ρ(r
)
dr v(r) ∼ 200 MeV fm3
V (r) =
V0
1 + e(r−R)/R
Mean potential method
The concept of mean potential (or mean field) strongly relies on the basic assumption
of independent particle motion, i.e. even if we know that the “real” nuclear potential
is complicated and nucleons are strongly correlated, some basic properties can be
adequately described assuming individual nucleons moving in an average potential (it
means that all the nucleons experience the same field).
a rough approximation could be
where v0 can be phenomenologically estimated to be
Then one can use a simple guess for V: harmonic oscillator, square well,
Woods-Saxon shape...