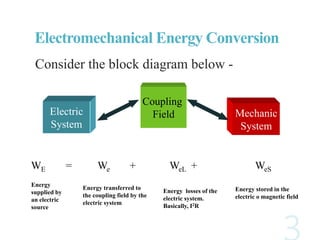
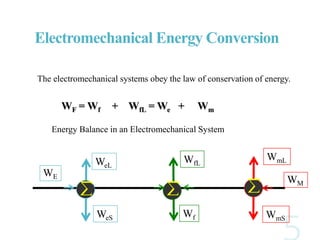
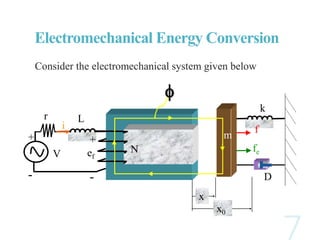
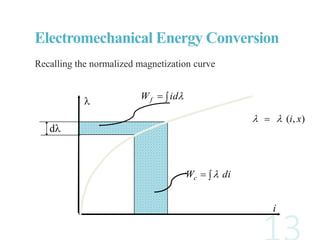
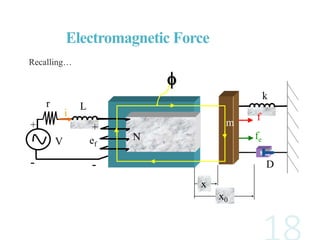
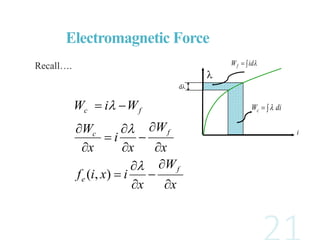
The document discusses electromechanical energy conversion in systems consisting of electric and mechanical components coupled through an interaction field. It presents equations showing that the total energy transferred to the coupling field (WF) is equal to the energy supplied by the electric system (WE) plus the energy supplied by the mechanical system (WM). The energy transfer is also affected by losses in the electric, mechanical and coupling field components. It further derives an expression for the electromagnetic force (fe) in terms of the device variables like current (i) and displacement (x).

1. Electro-mechanical
Energy Conversion

2. The electromechanical energy conversion theory allows
the representation of the electromagnetic force or torque in
terms of device variables, such as the currents and the
displacement of the mechanical systems.
An electromechanical system consists of an electric
system, a mechanical system, and a means whereby the
electric and mechanical systems can interact.
Electromechanical Energy Conversion

3. Consider the block diagram below -
Electric
System
Coupling
Field Mechanic
System
WE = We + WeL + WeS
Energy
supplied by
an electric
source
Energy transferred to
the coupling field by the
electric system
Energy losses of the
electric system.
Basically, I2R
Energy stored in the
electric o magnetic field
Electromechanical Energy Conversion

4. Electromechanical Energy Conversion
The energy transferred to the coupling field can be
represented by
WM = Wm + WmL + WmS
Energy
supplied by a
mechanical
source
Energy transferred to
the coupling field from
the mechanical system
Energy losses of the
mechanical system
Energy stored in the
moving member and
compliance of the
mechanical system
WF = We + Wm
Total energy
transferred to
the coupling field
Energy transferred to
the coupling field by
the electric system
Energy transferred to the
coupling field from the
mechanical system
WF = Wf + WfL
Energy stored in the
electric system
Energy dissipated as heat
(I2R)

5. Electromechanical Energy Conversion
The electromechanical systems obey the law of conservation of energy.
WF = Wf + WfL = We + Wm
  WE
WeL
WeS
WfL
WmL
Wf WmS
WM
Energy Balance in an Electromechanical System

6. If the losses are neglected, we will obtain the following formula
WF = We + Wm
Energy transferred to
the coupling field by
the electric system
Energy transferred to
the coupling field from
the mechanical system
Electromechanical Energy Conversion

7. Consider the electromechanical system given below
x
x0
N
+
-
ef
i
Lr
V
+
-
k
f
fe
D
m
f
Electromechanical Energy Conversion

8. The equation for the electrical system is-
fe
dt
di
LriV 
fexxK
dt
dx
D
dt
dx
mf  )( 02
2
Electromechanical Energy Conversion
The equation for the mechanical system is-

9. Electromechanical Energy Conversion
The total energy supplied by the electric source is -
 dt
dt
dx
fdxfWM
 





 dtie
dt
di
LridtiVW fE
The equation for the mechanical system is-

10. Substituting f from the equation of motion-

 dxfexxK
dt
dx
D
dt
dx
mdxfW
system
mechanical
thefrom
fieldcoupling
thetodtransferre
energyTotal
springtheinstored
EnergyPotential
(W all)
frictionthedue
lossHeat
masstheinstored
energyKinetic
E 























 

)( 02
2
Electromechanical Energy Conversion

11. dxfidtedW
dxfidteW
WWeW
Recall
dxfW
eff
eff
Mf
eM

 


*
Electromechanical Energy Conversion

12. If dx = 0 is assumed, then
0



dx
f
fEf
idW
dti
dt
d
idteWW


Electromechanical Energy Conversion

13. Recalling the normalized magnetization curve
),( xi 
d
  idWf
 diWc 
i
Electromechanical Energy Conversion

14. 0
),(
),(),(
),(












dx
f dii
i
xi
W
dx
x
xi
di
i
xi
d
xi




Electromechanical Energy Conversion

15. 0
),(
),(),(
),(

  

















dx
c d
xi
diW
dx
x
xi
d
xi
di
xii









Electromechanical Energy Conversion

16. From the previous relationship, it can be shown that for one coil
 
01
*
0
*
0
)(
)(

 


dxj
jjf
i
f
i
f
diW
case,generalaFor
idxLiW
ixLdiW


 
Electromechanical Energy Conversion

17. For two coupled coils
2
2
2221121
2
11
2
1
2
1
iLiiLiLWf 
 
 
n
p
n
q
qppqf iiLW
1 12
1
Electromechanical Energy Conversion
For the general case with n-coupled coils

18. Electromagnetic Force
Recalling…
x
x0
N
+
-
ef
i
Lr
V
+
-
k
f
fe
D
m
f

19. dt
d
e
dWdWdxf
dxfidteW
WWeW
f
fee
eff
Mf



 

Electromagnetic Force

20. fe
fe
dWdidxf
didti
dt
d
idtedW





dx
x
xi
di
i
xi
d






),(),( 

dx
x
xiW
di
i
xiW
dW
ff
f






),(),(
Substituting for d and dWf in fedx=id  dWf, it can be shown
  fe dW
x
ixif 




,
Electromagnetic Force

21. Recall….
d

 idWf
 diWc 
i
x
W
x
ixif
x
W
x
i
x
W
WiW
f
e
fc
fc


















),(
Electromagnetic Force

22. x
W
xif
x
W
x
i
x
ixif
x
W
x
ixif
WiWWWi
c
e
c
e
f
e
cfcf

























),(
),(
),(



Electromagnetic Force