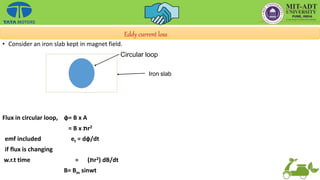
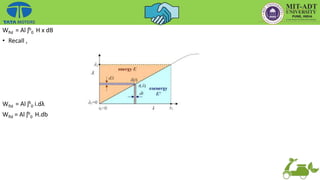
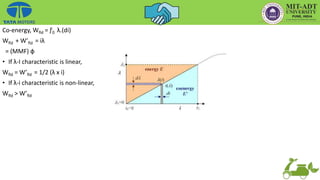
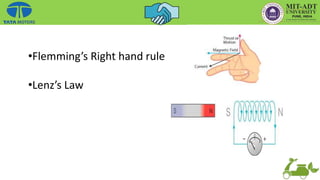
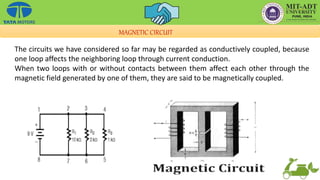
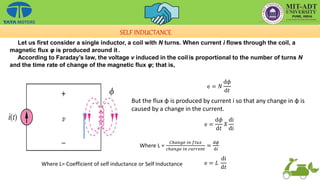
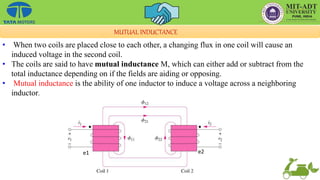
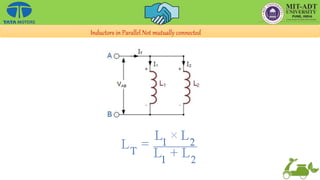
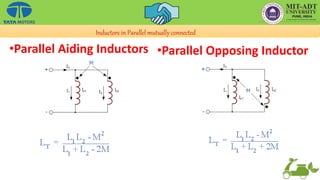
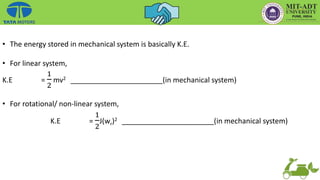
This document provides an overview of the basic principles of electrical machines, including electromagnetic induction, magnetic circuits, inductance, and electromechanical energy conversion. It discusses Faraday's laws of induction, self and mutually induced emf, magnetic circuits, inductance of coils in series and parallel configurations. It also covers concepts of mutual inductance, transformers, hysteresis effects, eddy currents, energy stored in magnetic systems, and the derivation of torque expression based on co-energy.

2. Course Conduction
of
Advanced Electric
Machines & Drives
M.Tech- Electric Vehicle Technology

3. UNIT I
Basic Principles of Electrical Machines
Contents:
• Magnetically coupled circuits
• Modelling linear and nonlinear magnetic circuits
• Electromechanical energy conversion : Principles of energy flow,
concept of field theory and co-energy
• Derivation of torque expression for various machines
• Inductance matrices

4. UNIT I
Basic Principles of Electrical Machines
Faraday’s Law of Electromagnetic Induction:
First Law
Second Law

5. UNIT I
Basic Principles of Electrical Machines
Faraday’s Law of Electromagnetic Induction:
•Statically Induced e.m.f.
•Dynamically induced e.m.f

6. •Flemming’s Right hand rule
•Lenz’s Law

7. Statically Induced e.m.f.
•Self Induced e.m.f.
•Mutually Induced e.m.f.

8. The circuits we have considered so far may be regarded as conductively coupled, because
one loop affects the neighboring loop through current conduction.
When two loops with or without contacts between them affect each other through the
magnetic field generated by one of them, they are said to be magnetically coupled.
MAGNETIC CIRCUIT

9. Let us first consider a single inductor, a coil with N turns. When current i flows through the coil, a
magnetic flux φ is produced around it.
According to Faraday’s law, the voltage v induced in the coilis proportional to the number of turns N
and the time rate of change of the magnetic flux φ; that is,
ⅇ = 𝑁
ⅆ𝜙
ⅆ𝑡
But the flux φ is produced by current i so that any change in φ is
caused by a change in the current.
ⅇ =
ⅆ𝜙
ⅆ𝑡
𝑋
ⅆⅈ
ⅆⅈ
Where L =
𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑓𝑙𝑢𝑥
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑐𝑢𝑟𝑟𝑒𝑛𝑡
=
ⅆ𝜙
ⅆ𝑖
ⅇ = 𝐿
ⅆⅈ
ⅆ𝑡
Where L= Coefficient of self inductance or Self Inductance
SELF INDUCTANCE

10. MUTUAL INDUCTANCE
• When two coils are placed close to each other, a changing flux in one coil will cause an
induced voltage in the second coil.
• The coils are said to have mutual inductance M, which can either add or subtract from the
total inductance depending on if the fields are aiding or opposing.
• Mutual inductance is the ability of one inductor to induce a voltage across a neighboring
inductor.
e1 e2

11. ⅇ2 = 𝑀21
ⅆⅈ1
ⅆ𝑡
Where M21 = mutual inductance of coil 2 w.r.t. coil 1
MUTUAL INDUCTANCE

12. ⅇ1 = 𝑀12
ⅆⅈ2
ⅆ𝑡
Where M21 = mutual inductance of coil 2 w.r.t. coil 1
MUTUAL INDUCTANCE

13. • Mutual inductances M12 and M21 are equal.
• They are referred as M.
• We refer to M as the mutual inductance between two coils.
• M is measured in Henry.
• Mutual inductance exists when two coils are close to each other.
• Mutual inductance effect exist when circuits are driven by time varying sources.
• Recall that inductors act like short circuits to DC.
MUTUAL INDUCTANCE
12 21
M M M
 

14. If the current ENTERS the dotted terminal of one coil, the reference polarity of the
mutual voltage in the second coil is POSITIVE at the dotted terminal of the
second coil.
DOT CONVENTION

15. • If the current LEAVES the dotted terminal of one coil, the reference polarity of
the mutual voltage in the second coil is NEGATIVE at the dotted terminal of
the second coil.
DOT CONVENTION

17. When both currents enter dotted terminals use positive sign for mutual term

18. Consider inductors connected in series not mutually connected to each other:
COIL IN SERIES

19. COIL IN SERIES
ITotal = IL1 = IL2 = IL3. . . = In
VTotal = VL1 + VL2 + VL3…. + Vn
V = L di/ dt
LT di/dt = L1 di/dt + L2 di/dt + L3 di/dt + . . . + Ln di/dt
LTotal = L1 + L2 + L3 + ….. + Ln

20. a) Series-aiding connection.
L=L1+L2+2M
b) Series-opposing connection.
L=L1+L2-2M
The total inductance of two coupled coils in series depend on the placement of the dotted ends of
the coils. The mutual inductances may add or subtract.
Mutually Connected Inductors in Series:
1) Cumulatively coupled or Series Aiding
2) Differentially coupled or Series opposing

21. • Transformers are constructed of two coils placed so that the charging flux developed by one
will link the other.
• The coil to which the source is applied is called the primary coil.
• The coil to which the load is applied is called the secondary coil.
• Three basic operations of a transformer are:
 Step up/down
 Impedance matching
 Isolation
MUTUAL INDUCTANCE

22. Inductors in Parallel Not mutually connected
Inductors are said to be connected together in Parallel when both of their
terminals are respectively connected to each terminal of another inductor or
inductors:

23. Inductors in Parallel Not mutually connected
• The voltage drop across all of the inductors in
parallel will be the same.
VL1= VL2 = VL3 = VAB …etc
By substituting di/dt in the above equation with v/L gives:

24. Inductors in Parallel Not mutually connected

25. Inductors in Parallel mutually connected
•Parallel Aiding Inductors
•Parallel Opposing Inductor

26. Inductors in Parallel mutually connected
•Parallel Aiding Inductors •Parallel Opposing Inductor

27. MUTUAL INDUCTANCE DEVICES

28. ELECTROMECHANICAL ENERGY CONVERSION
• The conversion of electrical energy into mechanical energy or vice versa is known as electromechanical energy .
• Energy can neither be created nor be destroyed. It is converted from one form of energy into another form.
Some form of energy is converted into desired form.
Some amount of energy is stored.
Some energy is dissipated.

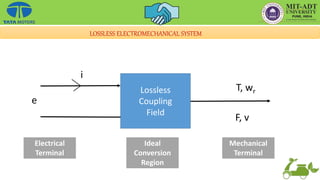
29. Energy Balance equation for motor:
Total electrical i/p = [Total mechanical output ]+ [Total energy stored]+ [Total energy dispatched] _1
Wei = [Wmo ]+[Wes+Wms]+[I2R + Magenetic losses in core + F/w losses]
Wei – ohmic loss = [Wmo+ Wms + Mechanical loss]+ [Wes + loss in coupling
field]
Therefore,
Welect = Wmech + Wfld ____2
Where
Welect = Wei = Net input electrical energy to the coupling field.
Wfld = Energy stored in coupling field
Wmech = Total energy converted from electrical to mechanical
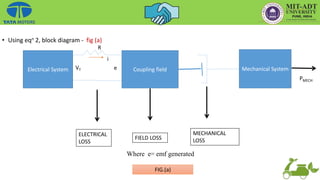
Using eqn 2, block diagram - fig (a)

30. • Using eqn 2, block diagram - fig (a)
PMECH
Electrical System Coupling field Mechanical System
ELECTRICAL
LOSS
FIELD LOSS
MECHANICAL
LOSS
VT e
R
i
Where e= emf generated
FIG.(a)

31. • The energy stored in mechanical system is basically K.E.
• For linear system,
K.E =
1
2
mv2 _______________________(in mechanical system)
• For rotational/ non-linear system,
K.E =
1
2
J(wr)2 _______________________(in mechanical system)

32. LOSSLESS ELECTROMECHANICAL SYSTEM
e
i
Lossless
Coupling
Field
T, wr
F, v
Electrical
Terminal
Ideal
Conversion
Region
Mechanical
Terminal

33. • The advantage of considering lossless coupling circuit leads to understanding the concept of electromechanical
conversion.
• For lossless conversion, let us differentiate eqn -------2,
W..r.t . Fig (a)
Welect = Wmech + Wfld
dWelect = dWmech + dWfld ------------3
Vt= e + ir ----------------4

34. Vt= e + ir ----------------(4)
Differential electrical input in time ‘dt’ is –
dWei = Vt i dt ----------------(5)
dWelect = dWei - Ohmic losses
= Vt i dt- I2 r
dWelect = (Vt-ir) idt -------(6)
e=Vt - ir ----------(7)
dWelect = ei dt --------(8)
Put eqn 8 in eqn 3,
eidt = dWmech + dWfld

35. This loop is called hysteresis
loop.
SOME IMPORTANT CONCEPTS

36. • Consider iron core connected to ac 1-Ø system.
l = average of length of magnetic path in ‘m’
H= NI/l …… AT/m
H α I
B= Ø/A Wb/m2 or T
B= µo µr H
In case of vacuum linear graph of B-H curve

37. • For any other mediums, µr plays a vital role and H enhances B.
B= µo µr H
• For ferromagnetic matertials,
• Dipole moments (H) get alligned with respect to multiplying factor of
µr.
• Magnetic dipoles present in ferromagnetic material.
• In the presence of H, they get alligned and enhanced B.
• At certain time, there is no change i.e; saturation
knee point on B-H curve point on graph beyond it Flattened

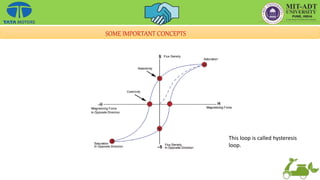
38. • There is hysteresis effect in B-H curve.
• Due to partial alignment of dipoles of the increase in the value of H,
dipoles become more and more alinged and reaches to a certain point,
from that point current started reversing.
[Refer point ‘x’ on B-H curve].
ʃ B H d v
• As per faraday’s law ,
• Flux linkage , λ =N Ø
= LI

39. emf included, e= dλ/dt
= N dØ/dt = L di/d
Vt = e + ir
= ir + L 2di/dE
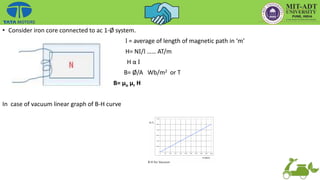
• As H ↑, B↑
Therefore , H= NI/l
B= µo µr H = µo µr (NI/l)
B= Ø/A
Ø=B.A
= µo µr (N x i x A/l)
= (µo µr A/l) N x I
But λ= NØ
=N [(µo µr A/l) Nx I]
λ= N2 (µo µr A/l) I

40. L= λ/i = N2 (µo µr /l) ……….. Henry
Therefore L= λ/i = N2 x Ø ………………H
where Ø= permeance
= µo µrA /l

41. Eddy current loss
• Consider an iron slab kept in magnet field.
Circular loop
Flux in circular loop, ф= B x A
= B x ‫ת‬r2
emf included et = dф/dt
if flux is changing
w.r.t time = (‫ת‬r2) dB/dt
B= Bm sinwt
Iron slab

42. dB/dt = wBm cos wt
et = ‫ת‬r2 wBm coswt
et (t)= Em coswt (Instantaneous emf) for 50 hz,w= 2‫ת‬f =100‫ת‬ ……rad/sec
i(t) = e(t)/R = Em/R cos wt
P(t)= i2R = Em2/R cos2 wt
Pav = 1/T ʃ P(t). dt
= 1/T Em2/R ʃcos2 wt.dt
Pav = (Em)2 /R → This amount of power lost in time “T”.
→ Eddy current loss
Eddy current loss → The alternating magnetic field in iron core sets up an induced emf around a closed path in the
crosssection in the proportion of area enclosed and this induced emf will intern cause the circulating current to flow.

43. Energy in magnetic system
• Consider singly excited magnetic system shown below .
• It is the magnetic system of an attracted armature relay.

44. • We have seen,
dWelect = dWmech + dWfld assuming armature at stationary
• Total flux linkages & induce emf eaquations, we know,
dWelect =(ei) dt where e= considering block diagram, λ= Nф
dWelect = idλ
• W.r.t eqn …a
dWelect = dWfld = id λ
= Ni.dф
dWfld = (MMf).dф
Integrating
ʃdWfld = ʃλ1
λ2 i.dλ=ʃф2
ф1 (MMF).dф
Wfld = ʃλ1
λ2 i.d λ = ʃф2
ф1 (MMF).dф
• Recall, H= Ni/l Ni= hl
ф= B x A dф= A.dB

45. Wfld = Al ʃb
0 H x dB
• Recall ,
Wfld = Al ʃλ
0 i.dλ
Wfld = Al ʃb
0 H.db

46. Co-energy, Wfld = ʃi
0 λ.(di)
Wfld + W’fld = iλ
= (MMF) ф
• If λ-I characteristic is linear,
Wfld = W’fld = 1/2 (λ x i)
• If λ-i characteristic is non-linear,
Wfld > W’fld

47. Derivation
• We have already studied the singly excited magnetic system.
• Energy stored in singly excited magnetic circuit is
dWelect = dWfld = idλ ……………………… 1
• The relationship between flux linkage and current for air gap length is shown in figure below :

48. • Al the increment field energy dWfld is shown by cross hatched lines.
• When flux linkage increases from 0 to λ, the energy stored in the field is given by,
Wfld = ʃλ
0 i.dλ …………………… 2
• The integral represents the shaded area OABO between Y-axis and the characteristics as shown in fig.
CO-energy:-

50. • Consider OABO area shown energy stored in magnetic field.
• Now the area OACO → between curve & x-axis
→ known as co-energy
• W’fld ʃi
0 λ.di ………………3
• Co-energy does not have any physical existance/ significance but it is useful in calculating force and torque
development in electromechanical system
• From graph,
Wfld + W’fld =(λ-i) ………………………….4
• To derive equation of torque , considering the movement of mech. Part/ armature w.r.t. singly excited magnetic
system .
• If the singly excited magnetic circuit is assumed to be linear, then this mechanical source movement can be
expressed in terms of –
→force
→distance ‘x’

51. • But in order to derive the torque, we must consider rotational motion.
• So for rotational motion the mechanical source is giving the distance which is displaced at angular displacement.
• Energy balance equation for singly excited magnetic system,
dWelect = dWmech + dWfld …………………… revised equation 1
Where,
dWfld =