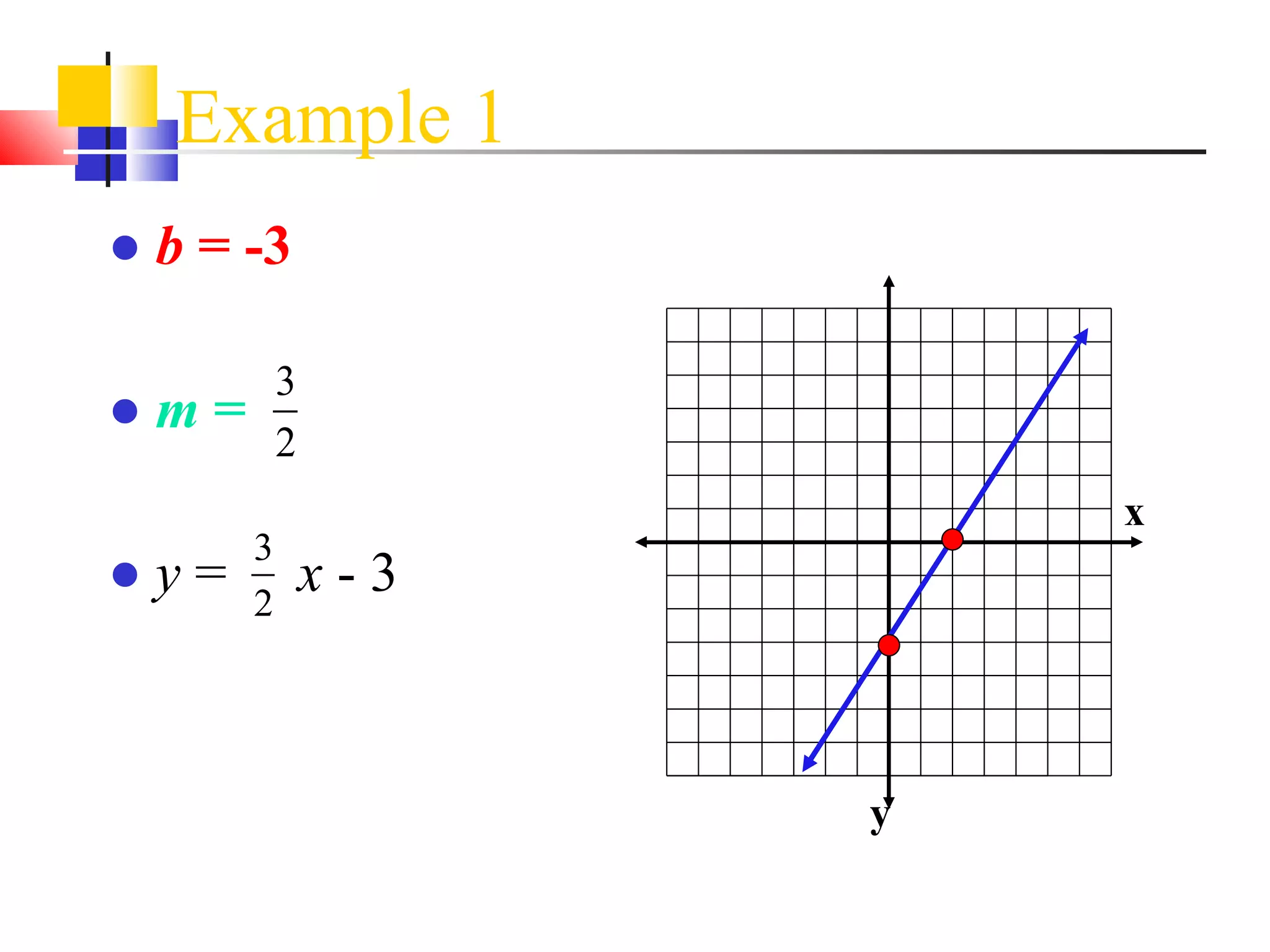
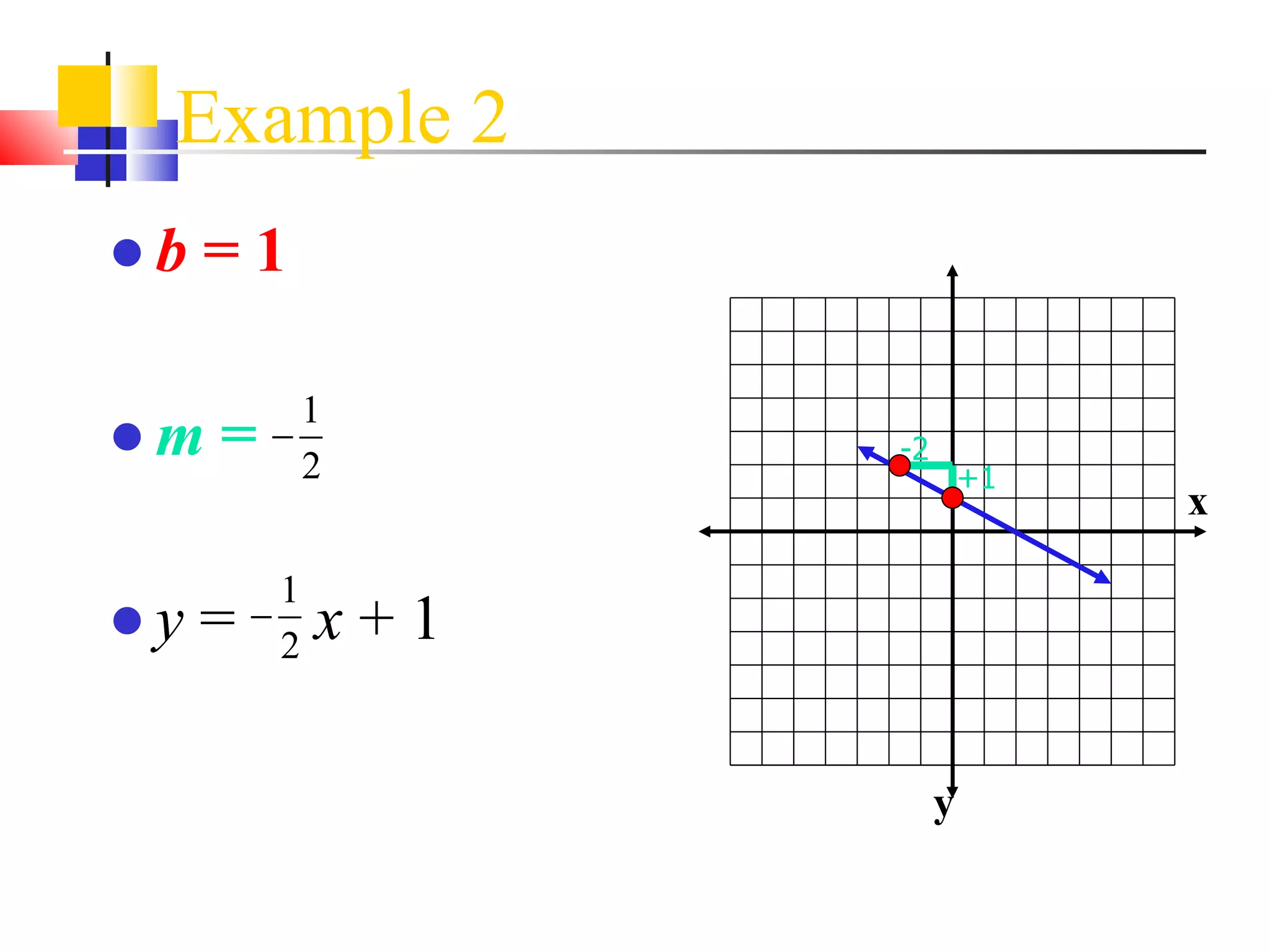
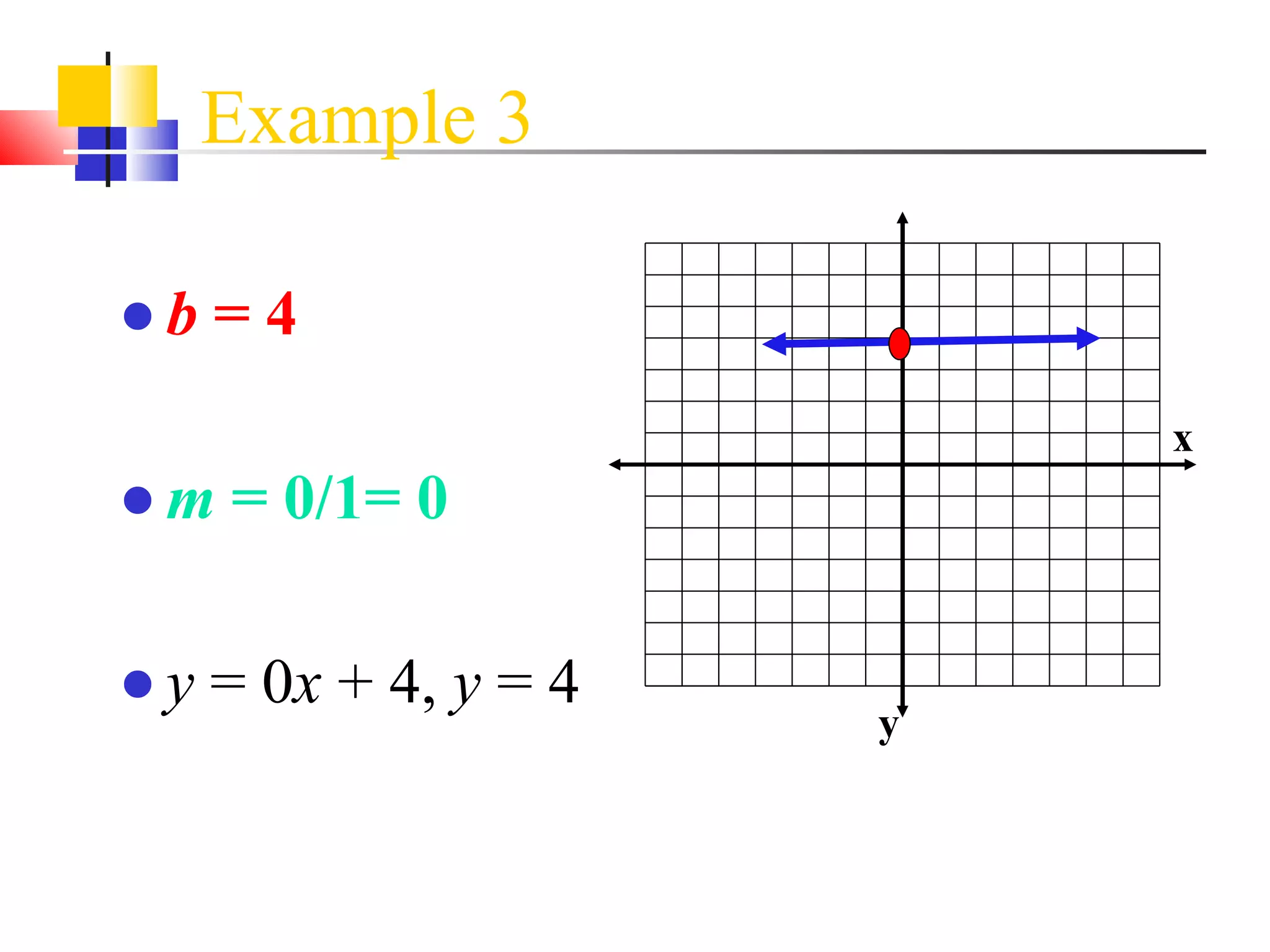
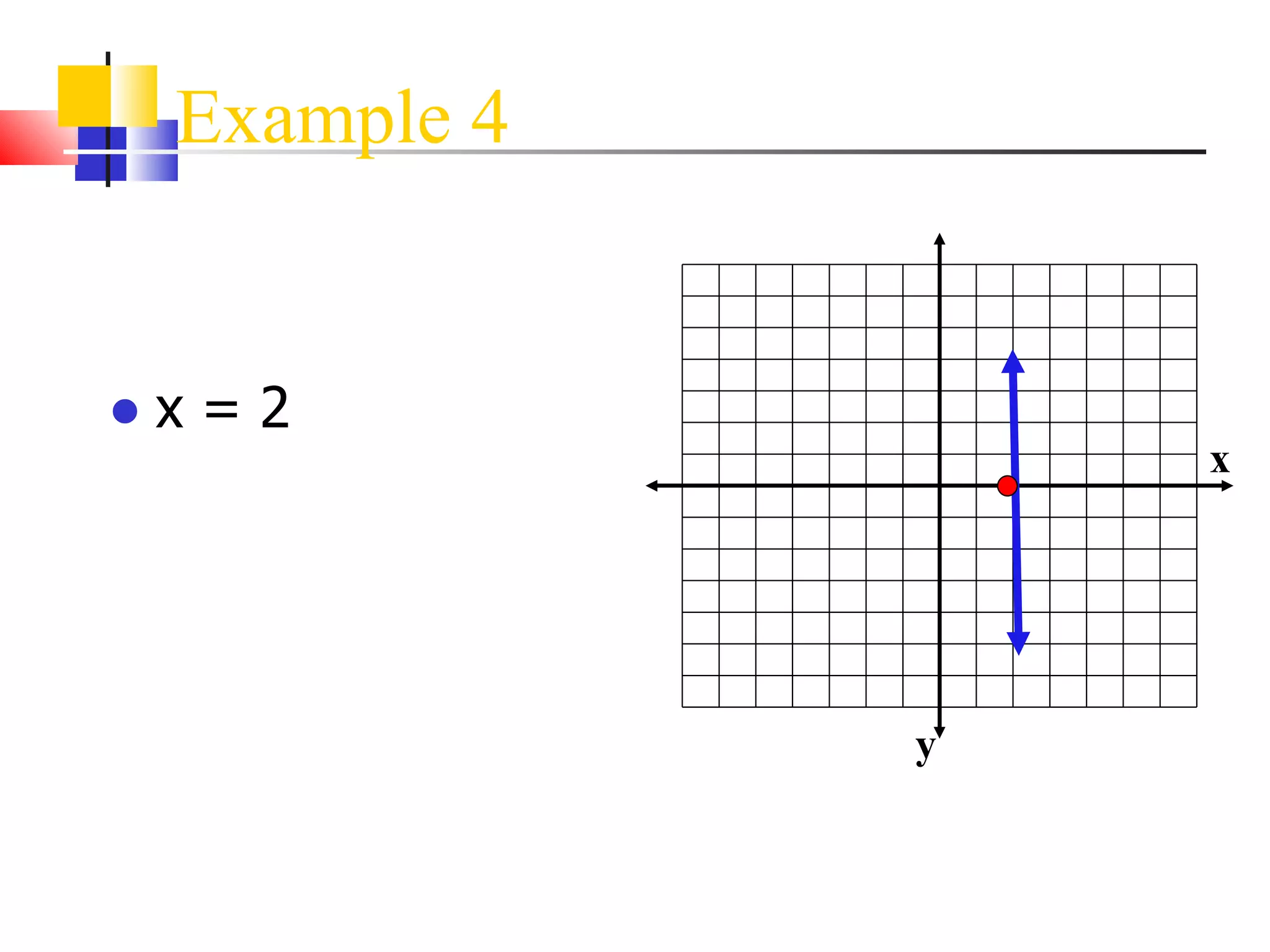
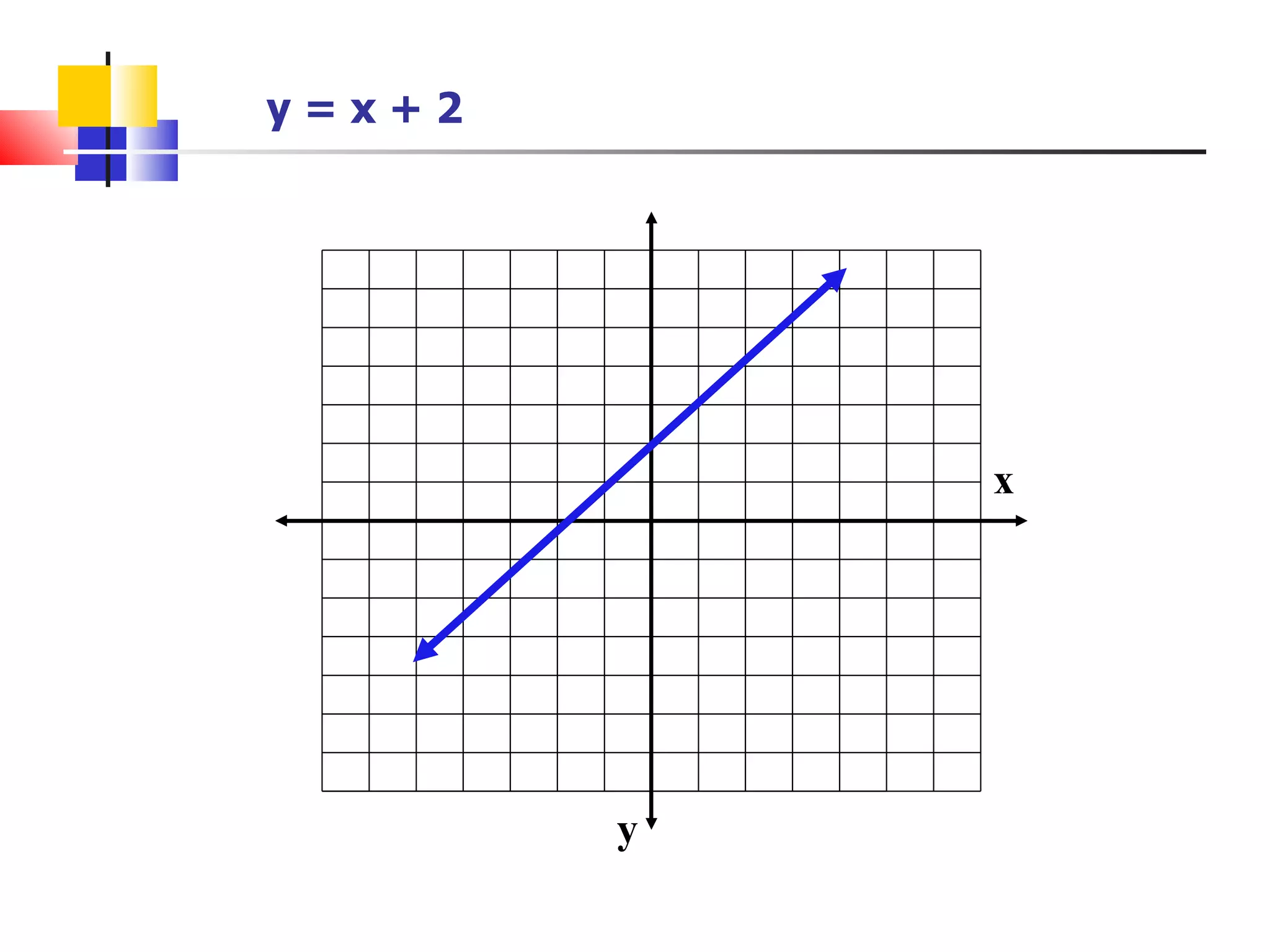
This document discusses different methods for finding the equation of a line, including: 1) Given the slope and y-intercept 2) Using a graph 3) Given a point and the slope 4) Given two points It provides examples of how to write the line equation using each method.

1. Equation of a Line 1. Slope and y -intercept 2. Graph 3. Slope and one point 4. Two points 5 . x - and y -intercepts

2. Find the Equation of the Line Given the Slope and y -intercept m = -3, b = 1 m = -2, b = -4 m = 0, b = 10 m = 1, b = 0 m = 0, b = 0 Substitute m and b into y = mx + b y = -3 x + 1 y = -2 x - 4 y = 0 x + 10, y = 10 y = 1 x + 0, y = x y = 0 x + 0, y = 0

3. Find the Equation of a Line Given the Graph Find the y -intercept from the graph. Count the slope from the graph.

4. Example 1 b = -3 m = y = x - 3 x y

5. Example 2 b = 1 m = y = x + 1 x y +1 -2

6. Example 3 b = 4 m = 0/1= 0 y = 0 x + 4, y = 4 x y

7. Example 4 x = 2 x y

8. Dude! You try one.

9. y = x + 2 x y

10. Find the Equation of a Line Given the Point and the Slope Use the Point-Slope Formula: is the given point Substitute m and into the formula

11. Example 1 Write the equation of the line with slope = -2 and passing through the point ( 3 , -5 ). y – (-5) = -2 ( x – 3 ) y + 5 = -2x + 6 y = -2x + 1

12. Remember this! Parallel lines have the same slope . m = m Perpendicular lines have a slope which is a negative reciprocal of the other. m = - ( 1/m )

13. Example 2 Find the equation of a line passing through ( 4,2 ) and parallel to y = 3x + 7. m = 3 x 1 = 4 ; y 1 = 2 y – 2 = 3 (x - 4) y – 2 = 3x - 12 y = 3x -10

14. Example 3 Find the equation of a line passing through ( 6,-3 ) and m = 3 perpendicular to y = 3x + 7. m = - 1/3 x 1 = 6 ; y 1 = -3 y – (-3) = -1/3 ( x – 6 ) y + 3 = -1/3 x + 2 y = - 1/3 x - 1

15. Seat work: ( ½ crosswise ) Answer page 98. #’s 25, 34, 37 and 40

16. Homework: (1/2 crosswise) Answer page 98. #’s 26, 35, 38 and 41.

17. Find the Equation of the Line Given Two Points Calculate the slope of the two points. Use one of the points and the slope to substitute into the Point-Slope formula.

18. Example Write the equation of the line that goes through the points (3, 2) and (5, 4). m = 2/2 or 1 y – 2 = 1 ( x -3 ) y – 2 = x -3 y = x - 1

19. Equation of a Line in diff. forms Slope – intercept form: y = mx + b y = x -1 Standard form : Ax + By = C x – y = 1 General form: Ax + By + C = 0 x – y – 1 = 0

20. Try this! Write the equation of the line that goes through the points (5, 2) and (-3, 7).

21. Find the Equation of the Line Given the x - and y - intercepts Write the intercepts as ordered pairs. The x -intercept 4 is the ordered pair (4, 0). The y -intercept -2 is the ordered pair (0, -2). Calculate the slope. Substitute the slope and the y -intercept ( b ) into the slope-intercept formula.

22. Example Write the equation of the line with x -intercept 3 and y -intercept 2. x -intercept 3 = (3, 0); y -intercept 2 = (0, 2) Slope: y = mx + b

23. Seatwork: (1/2 crosswise) Express your answer in different forms of equation. (slope-intercept , standard and general) 1.Find the equation of a line which goes through (1,-3) and (-5,2). 2. Find the equation of a line with x-intercept of 4 and y-intercept of -16.