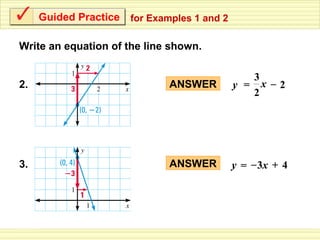
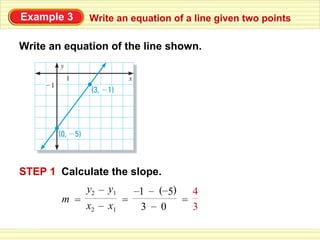
The document provides examples for writing linear equations in slope-intercept form (y=mx+b) given different representations of a line: 1) Given the slope (m) and y-intercept (b), write the equation. 2) Given a graph of the line, calculate the slope and y-intercept to write the equation. 3) Given the coordinates of two points on the line, calculate the slope and use it to write the equation. 4) Given an equation and a point that the line passes through, solve for the missing slope (m) or y-intercept (b) value.

1. Unit 6.1
Write Linear Equations in Slope-Intercept Form
TABLE
GRAPH EQUATION
RULE
• How can we recognize a linear equation?
• How do we know our rule is correct?
• What does the representation tell us?
• What are the connections between representations?

2. Example 1 Use slope and y-intercept to write an equation
Write an equation of the line with a slope of – 2 and a
y-intercept of 5.
y = mx + b Write slope-intercept form.
y = – 2x + 5 Substitute – 2 for m and 5 for b.

3. Example 2 Write an equation of a line from a graph
Write an equation of the line shown.
SOLUTION
–2 2
The slope of the line is m = = – .
5 5
The line crosses the y-axis at (0, 3).
So, the y-intercept is b = 3 .
y = mx + b Write slope-intercept form.
2 2
y = – x + 3 Substitute – for m and 3 for b.
5 5

4. Guided Practice for Examples 1 and 2
1. Write an equation of the line with a slope of 8 and a
y-intercept of – 7.
ANSWER y = 8x – 7

5. Guided Practice for Examples 1 and 2
Write an equation of the line shown.
3
2. ANSWER y = x –2
2
3. ANSWER y = – 3x + 4

6. Example 3 Write an equation of a line given two points
Write an equation of the line shown.
STEP 1 Calculate the slope.
y2 – y1 –1 – (–5) 4
m = = =
x2 – x1 3 – 0 3

7. Example 3 Write an equation of a line given two points
STEP 2 Write an equation of the line. The line crosses
the y-axis at (0, – 5 ). So, the y-intercept is b = – 5.
y = mx + b Write slope-intercept form.
4 4
y = x – 5 Substitute for m and – 5 for b.
3 3

8. Example 4 Find the slope or y-intercept given a point
Find the value of m or b if the given line passes through
the given point.
a. y = mx + 1; ( 3, – 2) b. y = 2x + b; (– 1, – 4)
SOLUTION
a. Substitute the coordinates of the given point into
the equation and solve for m.
y = mx + 1 Write original equation.
–2 = m ( 3) + 1 Substitute 3 for x and – 2 for y.
–3 = 3m Subtract 1 from each side.
–1 = m Divide each side by 3.

9. Example 4 Find the slope or y-intercept given a point
b. Substitute the coordinates of the given point into
the equation and solve for b.
y = 2x + b Write original equation.
–4 = 2(–1) + b Substitute –1 for x and – 4 for y.
–4 = –2 + b Multiply.
–2 = b Add 2 to each side.