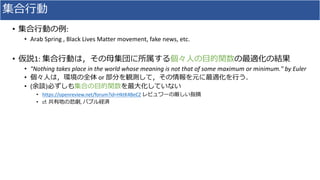
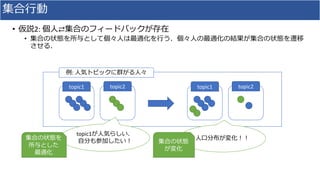
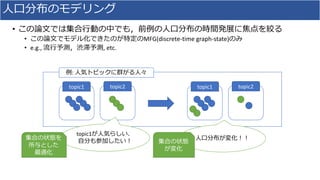
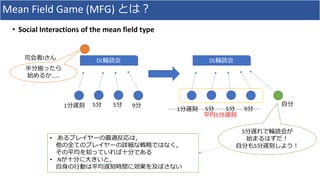
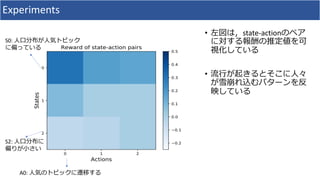
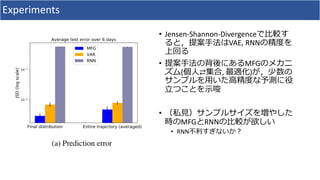
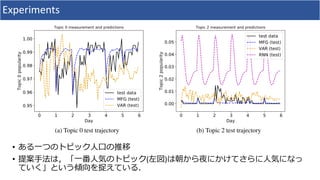
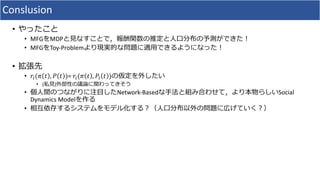
1. The document discusses using deep learning and mean field games to model collective behavior in large populations. 2. It proposes modeling collective behavior as a discrete-time graph-state mean field game and inferring the mean field game via Markov decision process optimization. 3. Experiments on modeling Twitter topics over time using this approach showed it outperformed vector autoregression and RNN baselines.

1. 1
DEEP LEARNING JP
[DL Papers]
http://deeplearning.jp/
“Learning deep mean field games for modeling large
population behavior"
or the intersection of machine learning and modeling collective processes

2. • : Learning deep mean fieldgamse for modeling large population behavior
• : Jiachen Yang, Xiaojing Ye, Rakshit Trivedi, Huan Xu, Hongyuan Zha
• Georgia Institute of Technology and Georgia State University
• : ICLR2018 (Oral)
• Scores: 10, 8, 8
• :
• Collective Behavior

3. • :
• Collective Behavior( )
• Mean Field Games(MFG)
• Pros:
• Cons: (= )
• : Inference of MFG via Markov Decision Process(MDP) Optimization
• MFG(discrete-time graph-state MFG) MDP
• MFG
•
• Twitter VAR, RNN

4. • :
• Arab Spring , Black Lives Matter movement, fake news, etc.
• 1:
• "Nothing takes place in the world whose meaning is not that of some maximum or minimum." by Euler
• or
• ( )
• https://openreview.net/forum?id=HktK4BeCZ
• cf. ,

5. • 2: ⇄
•
topic1 topic2 topic1 topic2
:
topic1

6. •
• MFG(discrete-time graph-state)
• e.g., , etc.
topic1 topic2 topic1 topic2
:
topic1

7. •
1. ( ⇄ )
2.
3.
• Mean Filed Game
1. 2. 3.
Time-Series-Analysis
(e.g., VAR)
Network-Analysis , ?,
Mean Field Game

8. Mean Field Game (MFG)
•
ØN-player ! → ∞
Ø
• e.g.,
•
•
•
• opinion network
• etc. ( : Gueant+ 2011)

9. Mean Field Game (MFG)
• MFG (Guent 2009):
•
• ! → ∞
•
• Social Interactions of the mean field type
•
•

10. Mean Field Game (MFG)
• Social Interactions of the mean field type
DL
1 5 5 9
DL
1 5 5 9
5
5
5
•
• N
……
I

11. ( ) Multi Agent Reinforcement Learning (MARL)
• Mean Field Multi-Agent Reinforcement Learning (Yang+ 2018)
• MARL
ØMARL j : !"
#
$, & = (#
$, & + *+,-~/(,-|&,,)[4"
#
($5
)]
Ø(#
$, & , 7($5
|&, $) &
Ø
•

12. Mean Field Game (MFG)
• MFG : (=- )
ØMFG agnostic
Ø
Ø MFG Toy-Problem
• Contribution:
• MFG Toy-Problem

13. Discrete-time graph-state MFG
• : Discrete-time graph-state MFG
• d
• !" # : t i
• $"%
&
: t, t+1 i j
• (Mean)
topic1 topic2 topic1 topic2
:
!' # =
2
3
!+ # =
1
3 !' # + 1 =
7
9
!' # + 2 =
2
9
$',+
&
=
1
6
, $+,'
&
=
2
3

14. Discrete-time graph-state MFG
• : Discrete-time graph-state MFG
• !"($ % , '" % ):
• $ % = $" % "*+
,
'"
-
= '",+
-
, … , '",,
-
i
• !"($ % , ' % )= !"($ % , '" % ) (where '-
= '+
-
, … , ',
-
)
topic1 topic2 topic1 topic2
:
!/($ % , '/ % )
$ %
2 '/ %
2 ( ⇄ )

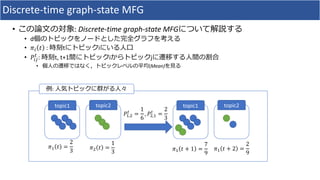
15. Discrete-time graph-state MFG
• MFG
• !"
#
= max
()
*
[," -#
, /"
#
+ ∑2 /"2
#
!2
#34
] (backward Hamilton-Jacobi-Bellman equation, HJB)
• -"
#34
= ∑2 /2"
#
-2
#
(forward Fokker-Planck equation)
• !"
6
: t i ( )
• -7
, !8
, ," -#
, /"
#
Dynamic Programing Trajectory -#
, !#
#97
8
• ," -#
, /"
#
•
ØHJB: Nash-Maximizer /"
#

16. Inference on MFG via MDP optimization
•
…
MDP
MFG Trajectory

17. Inference on MFG via MDP optimization
• MFG MDP
•
• MFG MDP
Ø
Ø MFG Forward-Path
• Settings
• States: !"
, n
• Actions: #"
, n
• Dynamics: !$
"%&
= ∑) #)$
"
!)
"
• Reward: * !"
, #"
= ∑$,&
-
!$
" ∑),&
-
#$)
"
.$)(!"
, #$
"
),

18. Inference on MFG via MDP optimization
• : MDP
MFG HJB, Fokker-Planck
HJB
Fokker-Planck
!
Nash-Maximizer!"

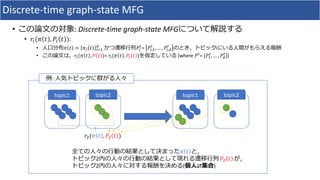
19. Inference on MFG via MDP optimization
•
1. ( ⇄ )
2.
3.
• MFG MDP
Øsingle-agent RL V∗
(%&
) = max
,
[. %&
, 0 + V∗
%&23
]
Ø ⇄
ØMDP

20. Experiments
• : Twitter
• d = 15 topics 15 ( ( , etc.) )
• n_timesteps=16, 16 1episode
• n_episodes = 27, 27
• Guided Cost Learning (Finn+ 2016)
• Forward-Path
•
• Deep
• : Vector Autoregression(VAR), RNN

21. Experiments
• state-action
•
S0:
A0:
S2:

22. Experiments
• Jensen-Shannon-Divergence
VAE, RNN
• MFG
( ⇄ , )
•
MFG RNN
• RNN

23. Experiments
•
• ( )

24. Conslusion
•
• MFG MDP
• MFG Toy-Problem
•
• !"($ % , ' % )= !"($ % , '" % )
• ( )
• Network-Based Social
Dynamics Model
•

25. • MFG VAR
or
•

26. References
• Gueant, Olivier. (2009). A reference case for mean field games models. Journal de
Mathématiques Pures et Appliquées. 92. 276-294. 10.1016/j.matpur.2009.04.008.
• Guéant O., Lasry JM., Lions PL. (2011) Mean Field Games and Applications. In: Paris-
Princeton Lectures on Mathematical Finance 2010. Lecture Notes in Mathematics, vol
2003. Springer, Berlin, Heidelberg
• Chelsea Finn, Sergey Levine, and Pieter Abbeel. Guided cost learning: Deep inverse
optimal control via policy optimization. In International Conference on Machine Learning,
pp. 49–58, 2016.
• Yaodong Yang, Rui Luo, Minne Li, Ming Zhou, Weinan Zhang, Jun Wang, Mean Field
Multi-Agent Reinforcement Learning, 2018, arxiv

27. • MFG :
• https://link.springer.com/content/pdf/10.1007%2Fs11537-007-0657-8.pdf
• MFG :
• https://www.sciencedirect.com/science/article/pii/S002178240900138X
• :
• https://terrytao.wordpress.com/2010/01/07/mean-field-equations/
• The causal mechanism for such waves is somewhat strange, though, due to the presence of the
backward propagating equation – in some sense, the wave continues to propagate because the
audience members expect it to continue to propagate, and act accordingly. (One wonders if these
sorts of equations could provide a model for things like asset price bubbles, which seem to be
governed by a similar mechanism.)