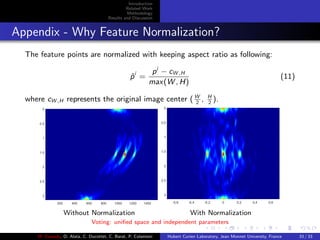
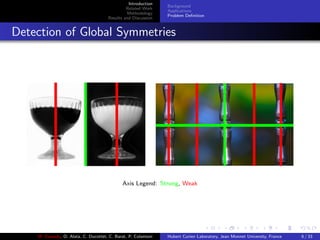
This document presents a methodology for detecting multiple reflection symmetries in images. It begins with an introduction and background on symmetry detection. It then discusses related work on intensity-based and edge-based symmetry detection methods. The proposed methodology extracts multi-scale edge segments from images and uses them to build a triangulation-based representation of local symmetry. A linear-directional kernel density estimation is applied to detect symmetry axes. The methodology is evaluated on standard symmetry detection datasets and compared to previous methods through precision-recall curves.

1. Introduction
Related Work
Methodology
Results and Discussion
Multiple Reflection Symmetry Detection via
Linear-Directional Kernel Density Estimation
M. Elawady1
, O. Alata1
, C. Ducottet1
, C. Barat1
, P. Colantoni2
1
Universit´e de Lyon, CNRS, UMR 5516, Laboratoire Hubert Curien,
Universit´e de Saint-´Etienne, Jean-Monnet, F-42000 Saint-´Etienne, France
2
Universit´e Jean Monnet, CIEREC EA n0
3068, Saint-´Etienne, France
17th
International Conference on Computer Analysis of Images and Patterns
UMR • CNRS • 5516 • SAINT-ETIENNE
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 1 / 33

2. Introduction
Related Work
Methodology
Results and Discussion
Table of Contents
1 Introduction
Background
Applications
Problem Definition
2 Related Work
Intensity-based Methods
Edge-based Methods
3 Methodology
Motivation
Algorithm Details
4 Results and Discussion
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 2 / 33

3. Introduction
Related Work
Methodology
Results and Discussion
Background
Applications
Problem Definition
Table of Contents
1 Introduction
Background
Applications
Problem Definition
2 Related Work
Intensity-based Methods
Edge-based Methods
3 Methodology
Motivation
Algorithm Details
4 Results and Discussion
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 3 / 33

4. Introduction
Related Work
Methodology
Results and Discussion
Background
Applications
Problem Definition
Bilateral Symmetry
1Image from book: The Photographer’s Eye by Michael Freeman
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 4 / 33

5. Introduction
Related Work
Methodology
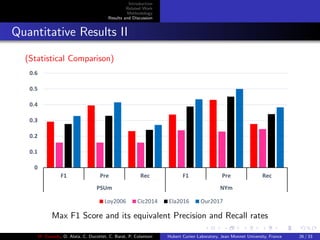
Results and Discussion
Background
Applications
Problem Definition
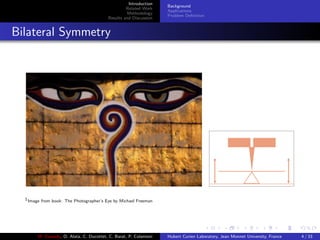
Bilateral Symmetry in Computer Vision
Medial Image Segmentation [1]
Aerial-based vehicle detection [2]
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 5 / 33

6. Introduction
Related Work
Methodology
Results and Discussion
Background
Applications
Problem Definition
Detection of Global Symmetries
Axis Legend: Strong, Weak
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 6 / 33

7. Introduction
Related Work
Methodology
Results and Discussion
Intensity-based Methods
Edge-based Methods
Table of Contents
1 Introduction
Background
Applications
Problem Definition
2 Related Work
Intensity-based Methods
Edge-based Methods
3 Methodology
Motivation
Algorithm Details
4 Results and Discussion
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 7 / 33

8. Introduction
Related Work
Methodology
Results and Discussion
Intensity-based Methods
Edge-based Methods
Baseline (Loy 2006) and its Successor (Mo 2011)
The general scheme (Loy and Eklundh 2006 [3]) consists of:
Disadvantages:
Depending mainly on the properties of hand-crafted features (i.e. SIFT).
For example: (smooth objects with noisy background)
little feature points =⇒ lost symmetry.
(Mo and Draper 2011 [4]) proposed refinements in the general scheme.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 8 / 33

9. Introduction
Related Work
Methodology
Results and Discussion
Intensity-based Methods
Edge-based Methods
First Work (Cic 2014)
Instead of SIFT, the general idea (Cicconet et al. 2014 [5]) is extracting a
regular set of wavelet segments with local edge amplitude and orientation.
Disadvantages:
Lacking neighborhood’s information inside the feature representation.
Depending on the scale parameter of the edge detector.
For example: (high texture objects with noisy background)
inferior symmetrical info =⇒ incorrect symmetry.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 9 / 33

10. Introduction
Related Work
Methodology
Results and Discussion
Intensity-based Methods
Edge-based Methods
State-of-Art (Ela 2016)
(Single Symmetry) Investigating Cicconet’s edge features [5] within Loy’s
scheme [3] by adding neighboring-pixel information.
(1) Mul�scale Edge
Segment Extrac�on
(2) Triangula�on based on
Local Symmetry Weights:
• Geometry Edge Orienta�ons (Cic)
• Local Texture Histogram (Loy)
(3) Vo�ng Space for Peak Detec�on with Handling
Orienta�on Discon�nuity.
θ
ρ
0
π
Legend: Groundtruth, Our2016, Loy2006, Mo2011, Cic2014
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 10 / 33

11. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Table of Contents
1 Introduction
Background
Applications
Problem Definition
2 Related Work
Intensity-based Methods
Edge-based Methods
3 Methodology
Motivation
Algorithm Details
4 Results and Discussion
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 11 / 33

12. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Proposed Idea
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 12 / 33

13. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Symmetry Detection Algorithm: Main Steps
Input Image
d) Symmetry Selection
a) Feature Extraction
Scale 1 Scale S
MagnitudeOrientationHistogram
Point 1 Point 2 Point P
c) Kernel Density Estimator
b) Feature Triangulation
Edge Magnitude
Symmetry Coefficient
Neighborhood Texture
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 13 / 33

14. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Multiscale Edge Segment Extraction I
Input Image
Scale 1
Scale 2
Scale S
Orientation 1
Orientation O/2
Orientation O
Amplitude Map
Orientation Map
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 14 / 33

15. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Multiscale Edge Segment Extraction II
A feature point pi
and its local edge characteristics (Ji
, φi
) are extracted
within each cell using a Morlet wavelet ψk,σ of constant scale σ and
varying orientation {φo
, o = 1 . . . O}.
Amplitude Map Orientation Map
Max
Amplitude
Corresponding
Orientation
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 15 / 33

16. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Multiscale Edge Segment Extraction III
Neighboring textural histogram hi
of size B:
hi
(b) =
r∈D(pi )
Jr
δφb−φr
, φb ∈ {
bπ
B
, b = 0 . . . B − 1, 8 ≤ B ≤ 32} (1)
where hi
is l1 normalized and circular shifted respect to the maximum
magnitude Ji
among the neighborhood window D(pi
).
0 36 72 108 144
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
#106
Magnitude Histogram
108 144 0 36 72
0
0.1
0.2
0.3
0.4
0.5
0.6
Histogram Count (hi)
0 36 72 108 144
0
500
1000
1500
2000
2500
3000
Frequency Histogram
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 16 / 33

17. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Symmetry Triangulation I
(Textural Information) Symmetry degree of the two regions around i and
j can be measured by comparing their corresponding local orientation
histograms hi
and ˜hj
(reverse histogram of hj
). Texture-based symmetry
measure is given by:
d(i, j) =
B
b=1
min(hi
(b), ˜hj
(b)) (2)
108 144 0 36 72
0
0.1
0.2
0.3
0.4
0.5
0.6
Histogram Count (hp)
72 36 0 144 108
0
0.1
0.2
0.3
0.4
0.5
0.6
Histogram Count (hq*)
1 2 3 4 5
0
0.1
0.2
0.3
0.4
0.5
0.6
Histogram Intersection
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 17 / 33

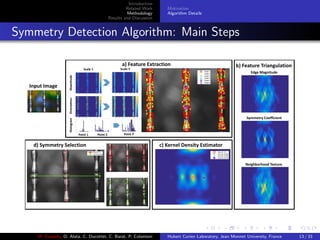
18. Introduction
Related Work
Methodology
Results and Discussion
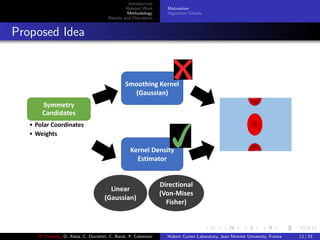
Motivation
Algorithm Details
Symmetry Triangulation II
(Edge Information) Semi-dense edge magnitude m(i, j) and mirror
symmetry coefficient c(i, j) {similar to cosine distance} are defined as [5]:
m(i, j) = Ji
Jj
(3)
c(i, j) = |τi
S(T⊥
ij )τj
| (4)
where τi
= [cos(φi
), sin(φi
)], and S(.) is a reflection matrix.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 18 / 33

19. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Symmetry Triangulation III
The candidate axis is parametrized by angle θn, and displacement ρn and
has pairwise symmetry weight ωn = ωi,j (i = j and σi
= σj
) is defined as:
ωn = ω(ˆpi
, ˆpj
) = m(i, j) c(i, j) d(i, j) (5)
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 19 / 33

20. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Kernel Density Estimation I
(Linear: Displacement) Linear kernel density estimator fl (.) is defined as
fl (x; g) =
1
Ng
N
n=1
G(
x − ρn
g
) | G(u) =
1
(2π)
1
2
e− 1
2
|u|2
(6)
where G(.) is a Gaussian kernel with bandwidth parameter g.
(Directional: Angle) Directional kernel density estimator fd (.) is defined as:
fd (y; k) =
C(k)
N
N
n=1
L(yT
µn; k) | L(x; k) = ekx
, C(k) =
1
2πS(0, k)
(7)
where L(.) is a von-Mises Fisher kernel with concentration parameter k, and
normalization constant C(k). S(.) is the modified Bessel function of the first
kind.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 20 / 33

21. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Kernel Density Estimation II
Thanks for the linear-directional density estimator fl,d (.) [6]. We define
the extended weighted version ˆfl,d (.) as:
ˆfl,d (x, y; g, k) =
C(k)
Ng
N
n=1
ωnG(
x − ρn
g
)L(yT
µn; k) (8)
y = [cos(θ), sin(θ)], µn = [cos(θn), sin(θn)]
assuming that linear and directional data are independent resulting dot
product between accompanying kernels.
B
A2 A1 A3
B
B
A2 A1 A3
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 21 / 33

22. Introduction
Related Work
Methodology
Results and Discussion
Motivation
Algorithm Details
Kernel Density Estimation III
B
A2 A1 A3
Input Image
A2
A1
A3
Linear KDE fl (.)
[A1,A2,A3]
B B
Directional KDE fd (.)
Edge Magnitude mn(.) Symmetry Coefficient cn(.) Neighborhood Texture dn(.)
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 22 / 33

23. Introduction
Related Work
Methodology
Results and Discussion
Table of Contents
1 Introduction
Background
Applications
Problem Definition
2 Related Work
Intensity-based Methods
Edge-based Methods
3 Methodology
Motivation
Algorithm Details
4 Results and Discussion
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 23 / 33

24. Introduction
Related Work
Methodology
Results and Discussion
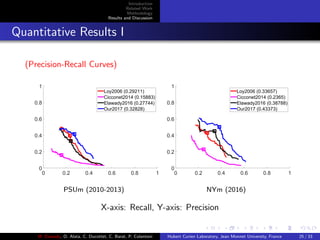
Evaluation Details
Datasets:
PSUm dataset: Liu’s vision group proposed a symmetry groundtruth
[7, 8] for Flickr images (# images = 142, # symmetries = 479) in
ECCV2010, CVPR2011 and CVPR2013.
NYm dataset: Cicconet et al. [9] presented a new symmetry
database (# images = 63, # symmetries = 188) in 2016.
Evaluation Metrics:
True Positive [8]:
ang(SC, GT) < 10◦
(9)
dist(CenSC , CenGT ) < 20% × min(LenSC , LenGT ) (10)
Precision, Recall, and Maximum F1 Score
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 24 / 33

25. Introduction
Related Work
Methodology
Results and Discussion
Quantitative Results I
(Precision-Recall Curves)
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Loy2006 (0.29211)
Cicconet2014 (0.15883)
Elawady2016 (0.27744)
Our2017 (0.32828)
PSUm (2010-2013)
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Loy2006 (0.33657)
Cicconet2014 (0.2365)
Elawady2016 (0.38788)
Our2017 (0.43373)
NYm (2016)
X-axis: Recall, Y-axis: Precision
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 25 / 33

26. Introduction
Related Work
Methodology
Results and Discussion
Quantitative Results II
(Statistical Comparison)
Max F1 Score and its equivalent Precision and Recall rates
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 26 / 33

27. Introduction
Related Work
Methodology
Results and Discussion
Qualitative Results I - PSUm
Columns: (1) GT, (2) Our, (3) Ela2016 [10], and (4) Loy2006 [3]
Top 5 detections: red, yellow, green, blue, and magenta.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 27 / 33

28. Introduction
Related Work
Methodology
Results and Discussion
Qualitative Results II - NYm
Columns: (1) GT, (2) Our, (3) Ela2016 [10], and (4) Loy2006 [3]
Top 5 detections: red, yellow, green, blue, and magenta.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 28 / 33

29. Introduction
Related Work
Methodology
Results and Discussion
Conclusion
Summary:
1 A weighted joint density estimator is proposed to handle both orientation and
displacement information.
2 A reliable detection framework is developed for global multiple symmetries.
Future work:
1 The proposed detection can be improved using a continuous maximal-seeking
technique to avoid over-extended axes.
2 Entropy-based balance measure can be introduced to describe the existence and
degree of global axes inside an image.
3 Possibility of integration within retrieval systems for artistic photographs and
paintings in museums
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 29 / 33

30. Introduction
Related Work
Methodology
Results and Discussion
References I
[1] F. Abdolali, R. A. Zoroofi, Y. Otake, and Y. Sato, “Automatic segmentation of
maxillofacial cysts in cone beam ct images,” Computers in biology and medicine,
vol. 72, pp. 108–119, 2016.
[2] S. Ram and J. J. Rodriguez, “Vehicle detection in aerial images using multiscale
structure enhancement and symmetry,” in Image Processing (ICIP), 2016 IEEE
International Conference on, pp. 3817–3821, IEEE, 2016.
[3] G. Loy and J.-O. Eklundh, “Detecting symmetry and symmetric constellations of
features,” in Computer Vision–ECCV 2006, pp. 508–521, Springer, 2006.
[4] Q. Mo and B. Draper, “Detecting bilateral symmetry with feature mirroring,” in
CVPR 2011 Workshop on Symmetry Detection from Real World Images, 2011.
[5] M. Cicconet, D. Geiger, K. C. Gunsalus, and M. Werman, “Mirror symmetry
histograms for capturing geometric properties in images,” in Computer Vision
and Pattern Recognition (CVPR), 2014 IEEE Conference on, pp. 2981–2986,
IEEE, 2014.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 30 / 33

31. Introduction
Related Work
Methodology
Results and Discussion
References II
[6] E. Garc´ıa-Portugu´es, R. M. Crujeiras, and W. Gonz´alez-Manteiga, “Kernel
density estimation for directional–linear data,” Journal of Multivariate Analysis,
vol. 121, pp. 152–175, 2013.
[7] I. Rauschert, K. Brocklehurst, S. Kashyap, J. Liu, and Y. Liu, “First symmetry
detection competition: Summary and results,” tech. rep., Technical Report
CSE11-012, Department of Computer Science and Engineering, The
Pennsylvania State University, 2011.
[8] J. Liu, G. Slota, G. Zheng, Z. Wu, M. Park, S. Lee, I. Rauschert, and Y. Liu,
“Symmetry detection from realworld images competition 2013: Summary and
results,” in Computer Vision and Pattern Recognition Workshops (CVPRW),
2013 IEEE Conference on, pp. 200–205, IEEE, 2013.
[9] M. Cicconet, V. Birodkar, M. Lund, M. Werman, and D. Geiger, “A convolutional
approach to reflection symmetry,” Pattern Recognition Letters, 2017.
[10] M. Elawady, C. Barat, C. Ducottet, and P. Colantoni, “Global bilateral symmetry
detection using multiscale mirror histograms,” in International Conference on
Advanced Concepts for Intelligent Vision Systems, pp. 14–24, Springer, 2016.
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 31 / 33

32. Introduction
Related Work
Methodology
Results and Discussion
Questions?
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 32 / 33

33. Introduction
Related Work
Methodology
Results and Discussion
Appendix - Why Feature Normalization?
The feature points are normalized with keeping aspect ratio as following:
ˆpi
=
pi
− cW ,H
max(W , H)
(11)
where cW ,H represents the original image center (W
2
, H
2
).
Without Normalization With Normalization
Voting: unified space and independent parameters
M. Elawady, O. Alata, C. Ducottet, C. Barat, P. Colantoni Hubert Curien Laboratory, Jean Monnet University, France 33 / 33