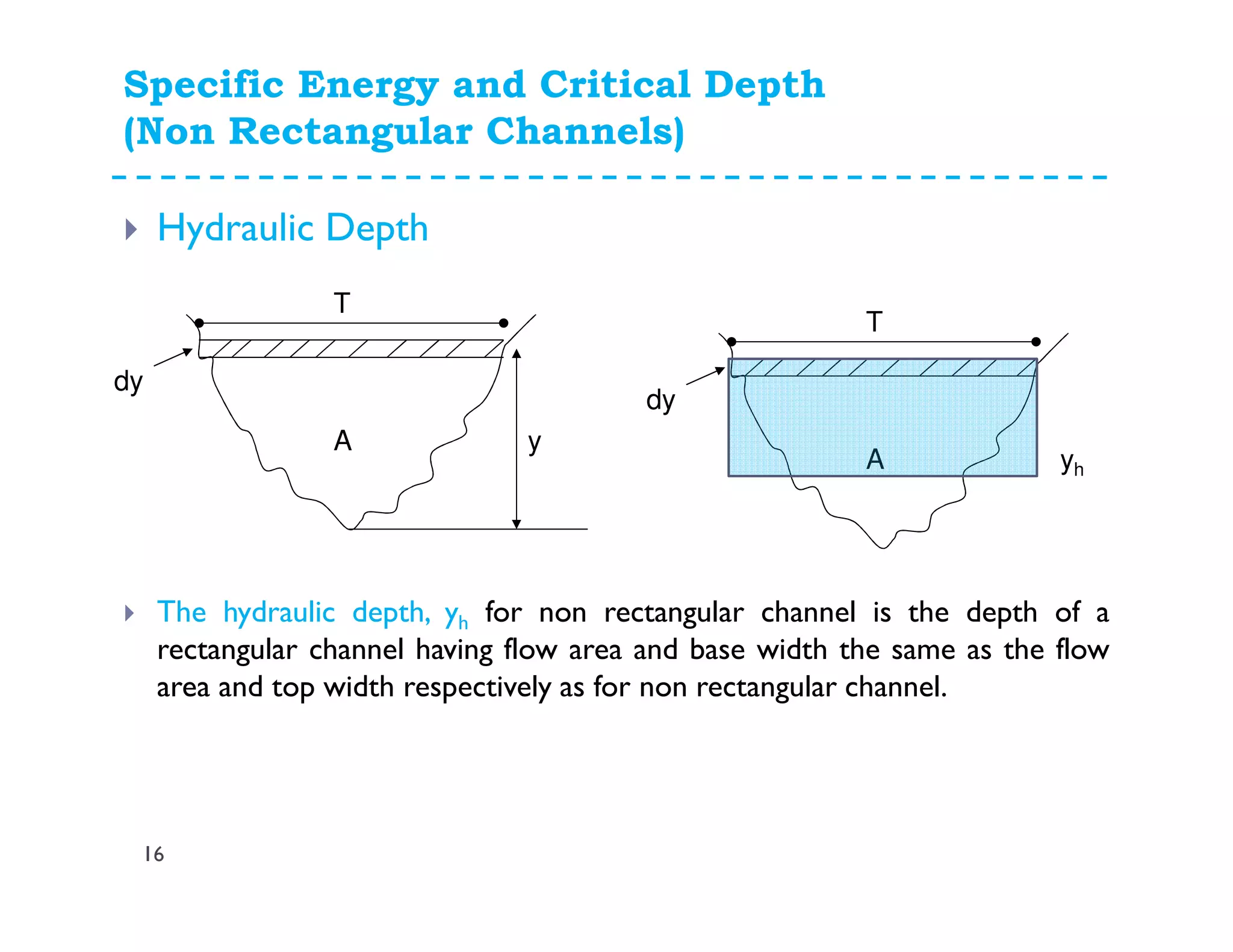
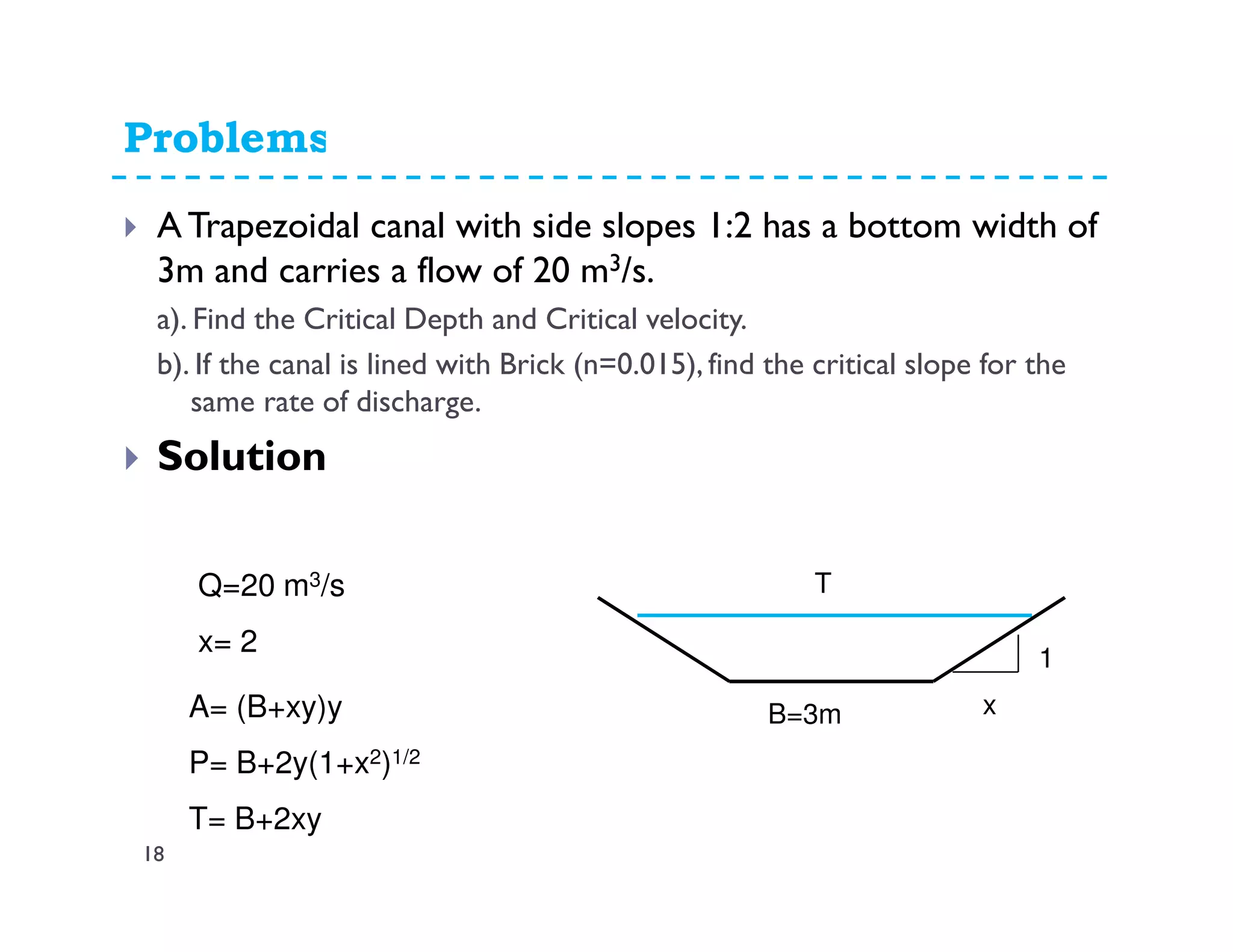
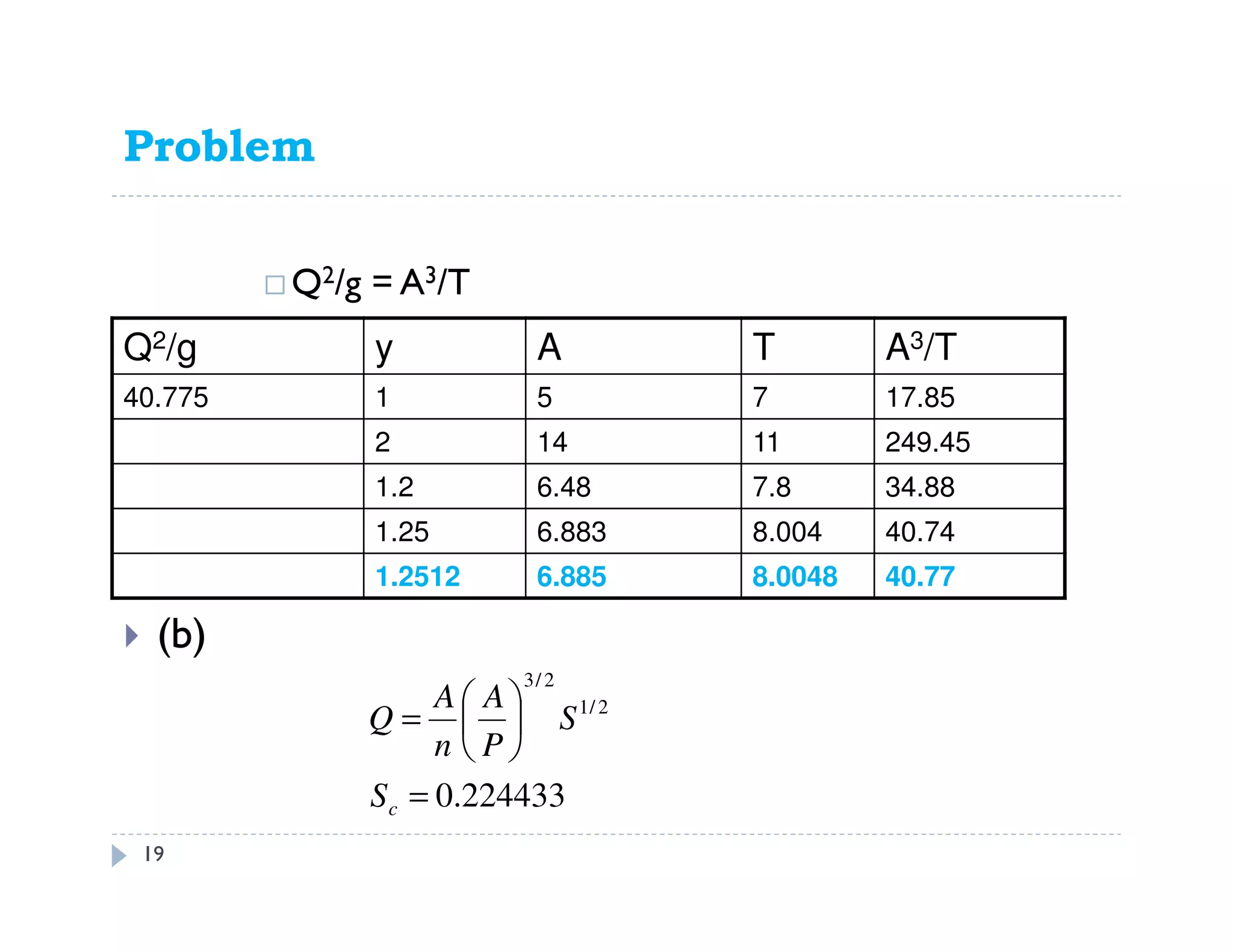
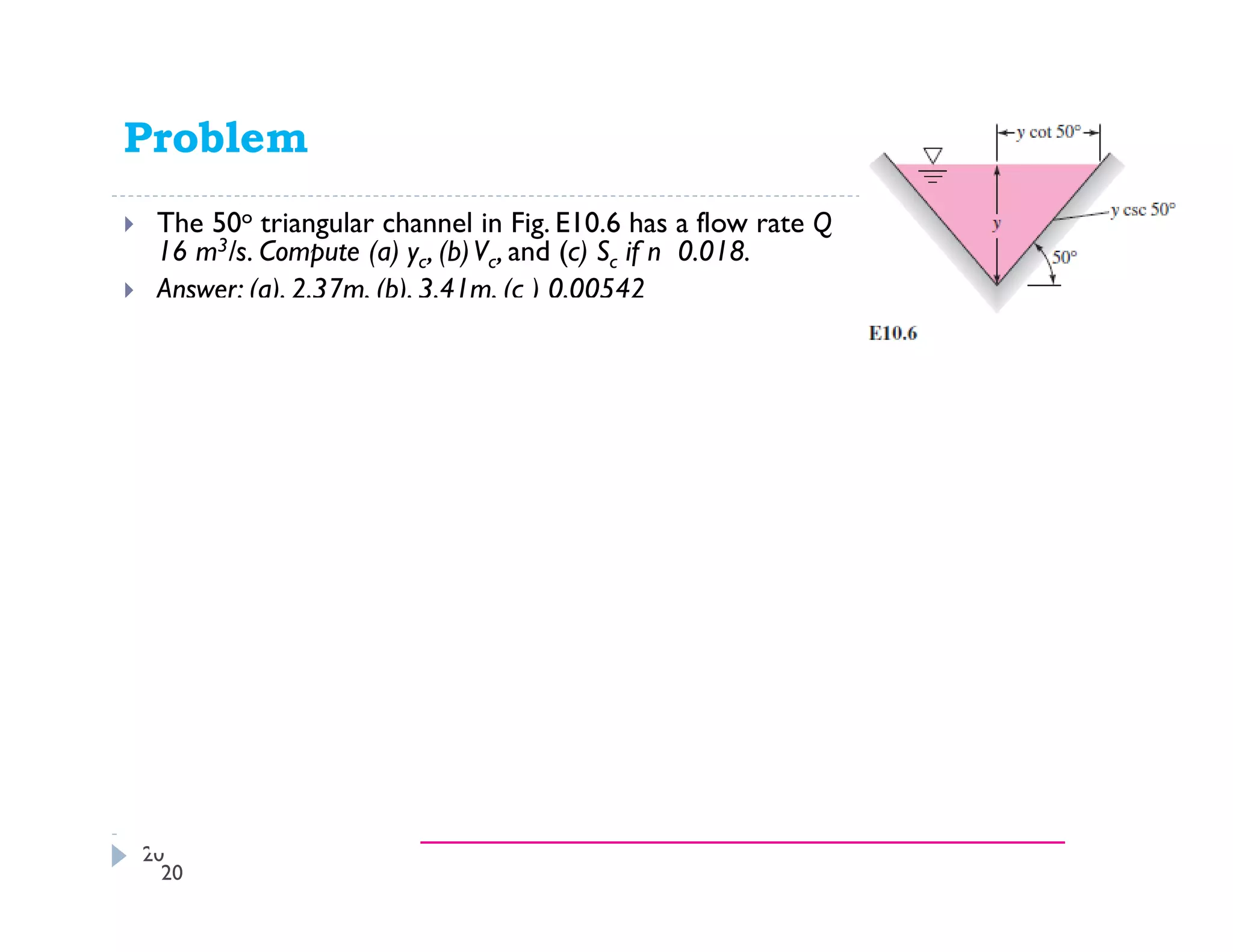
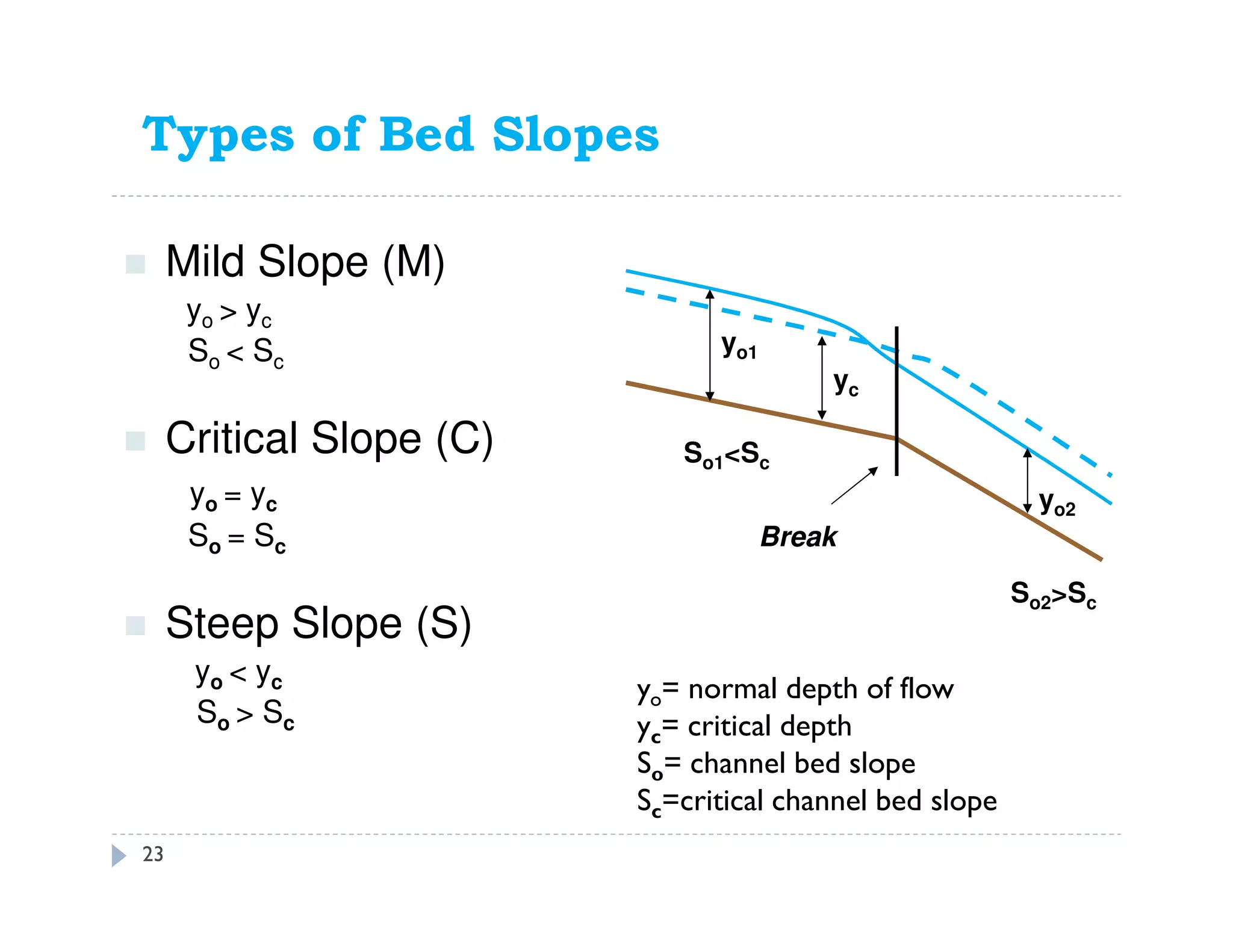
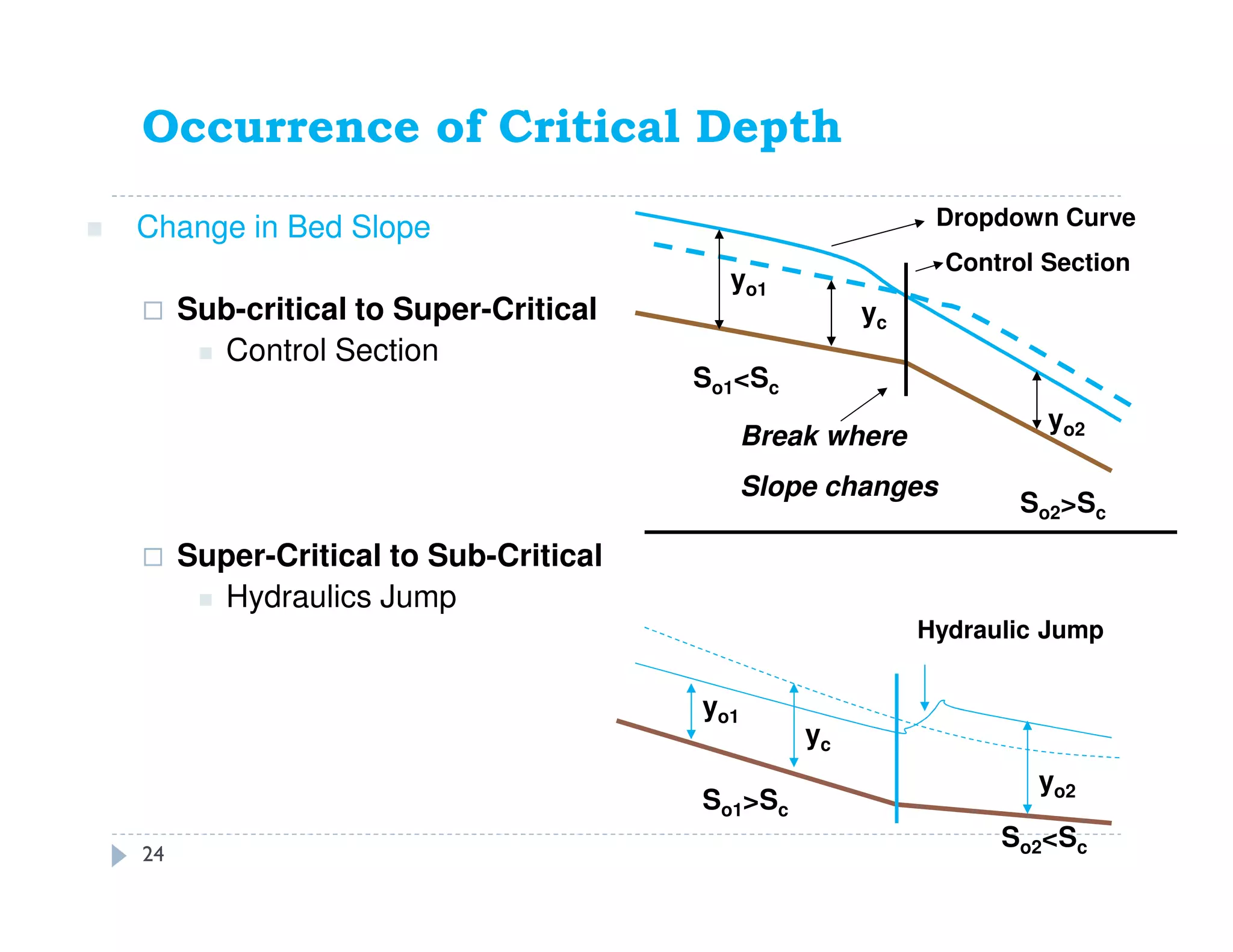
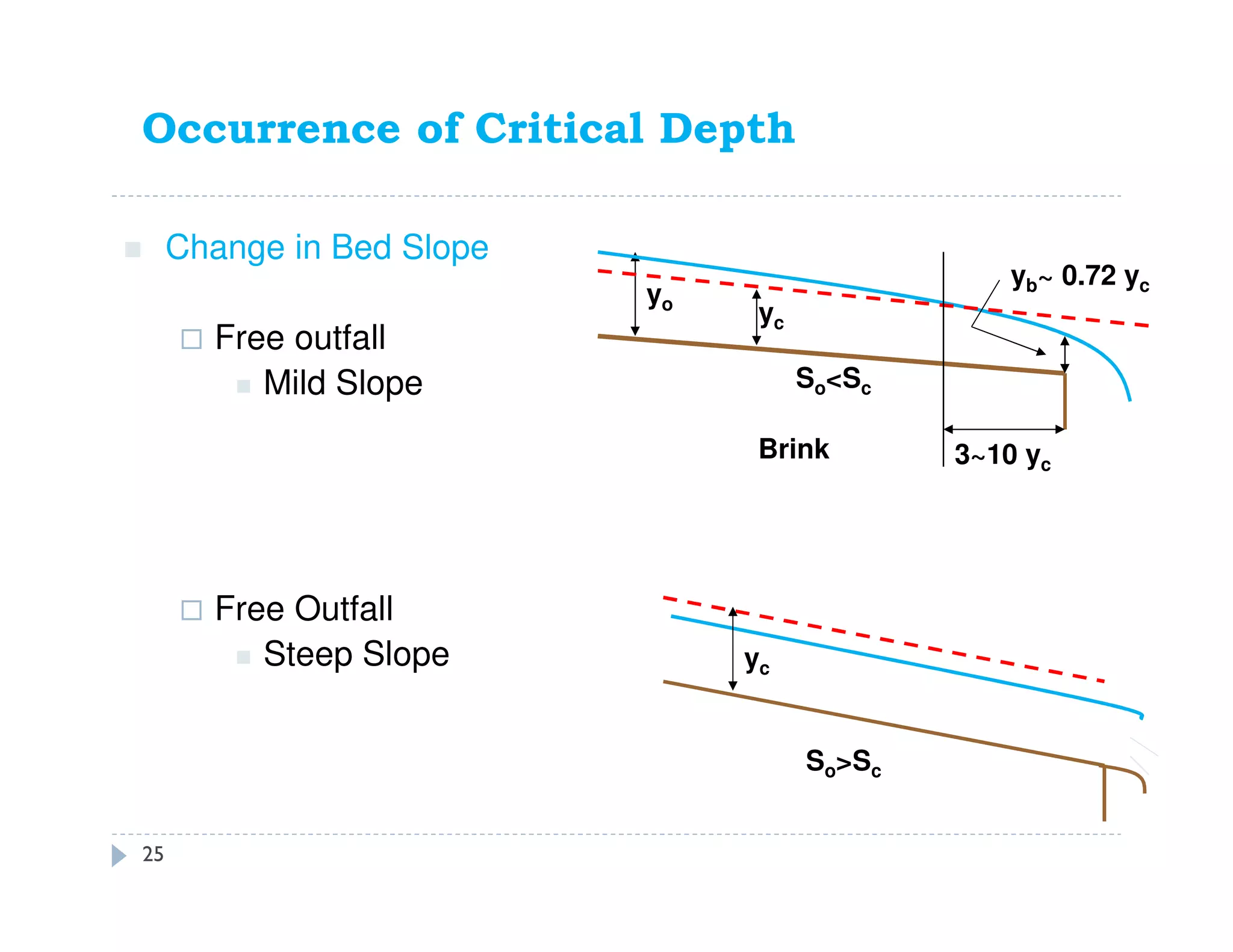
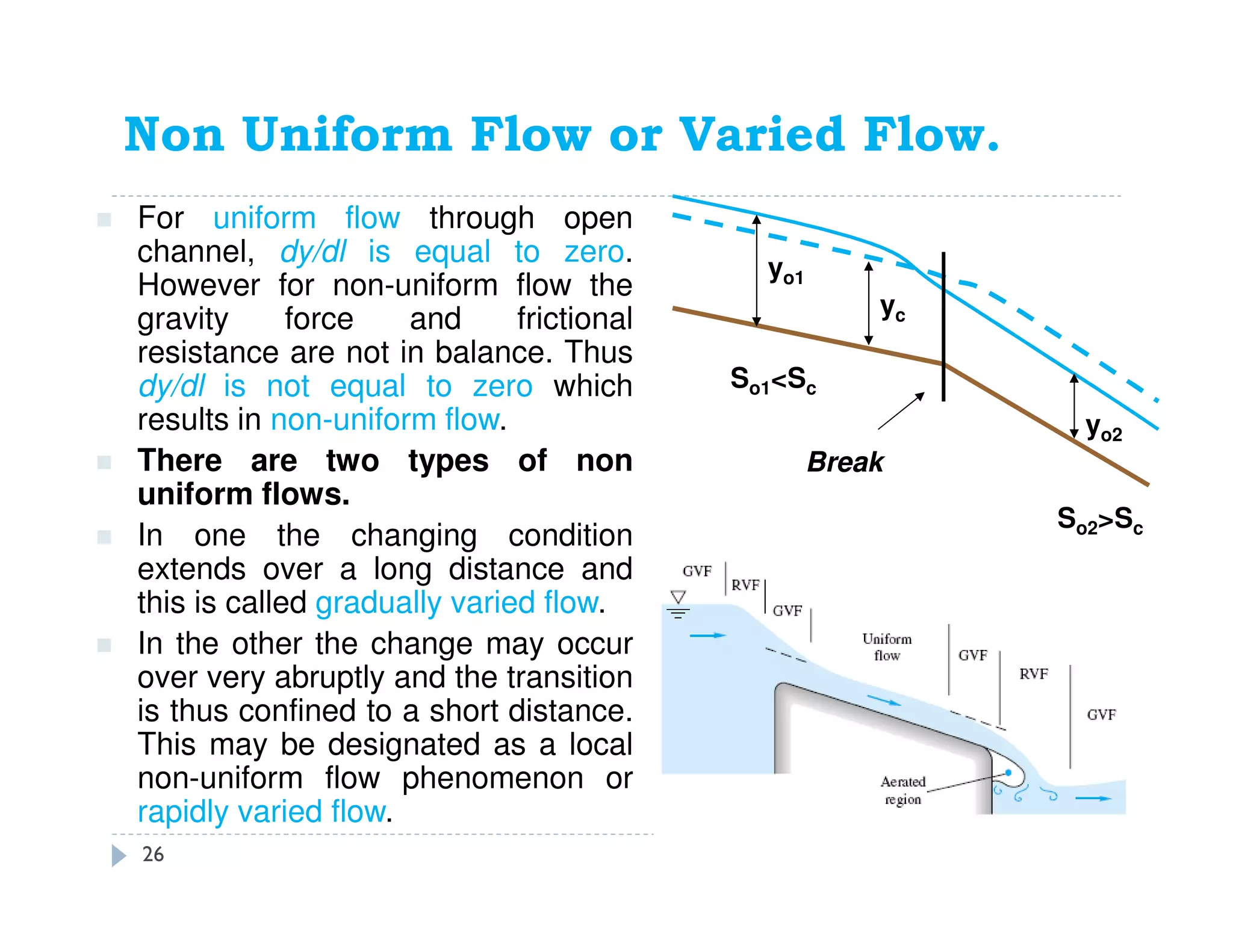
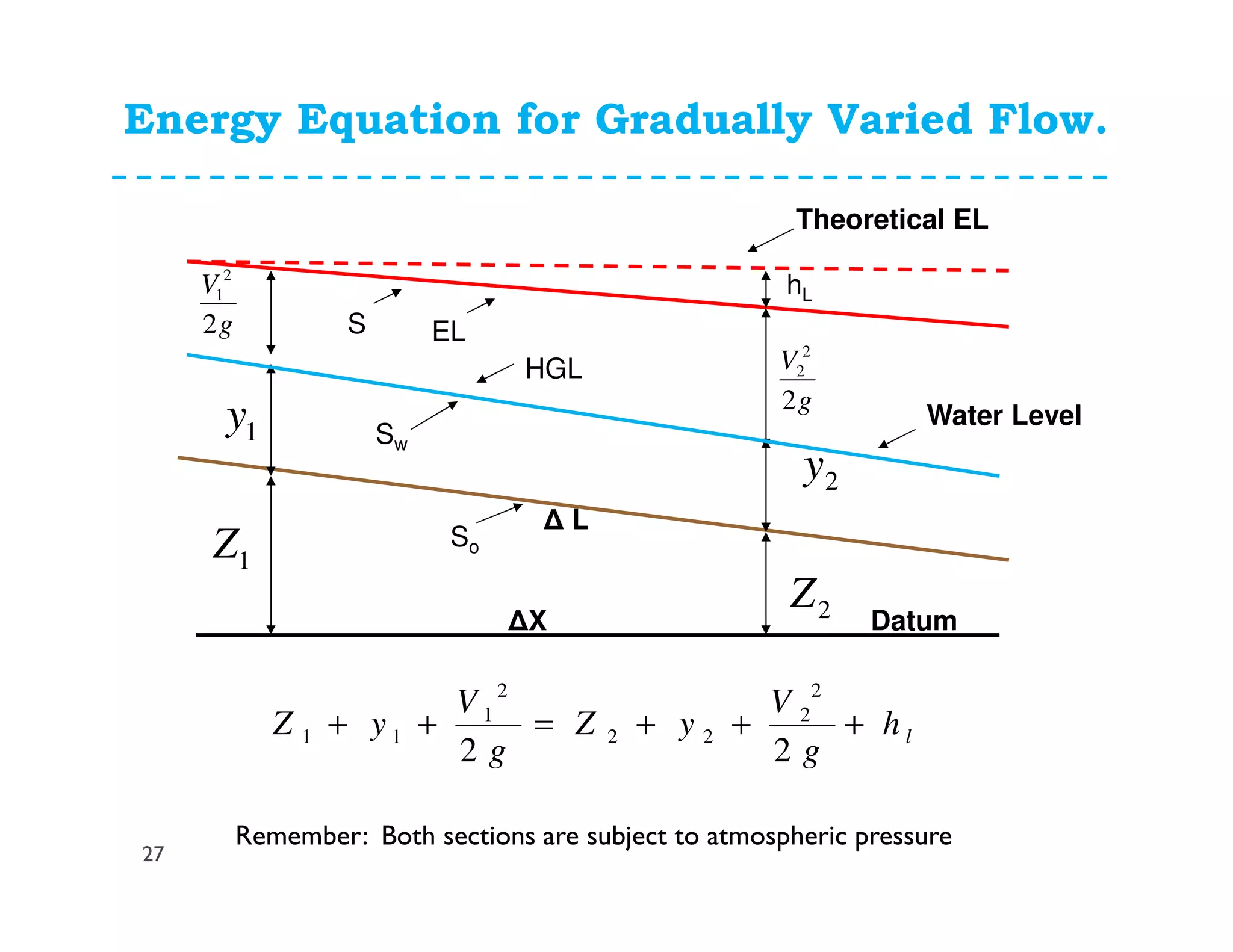
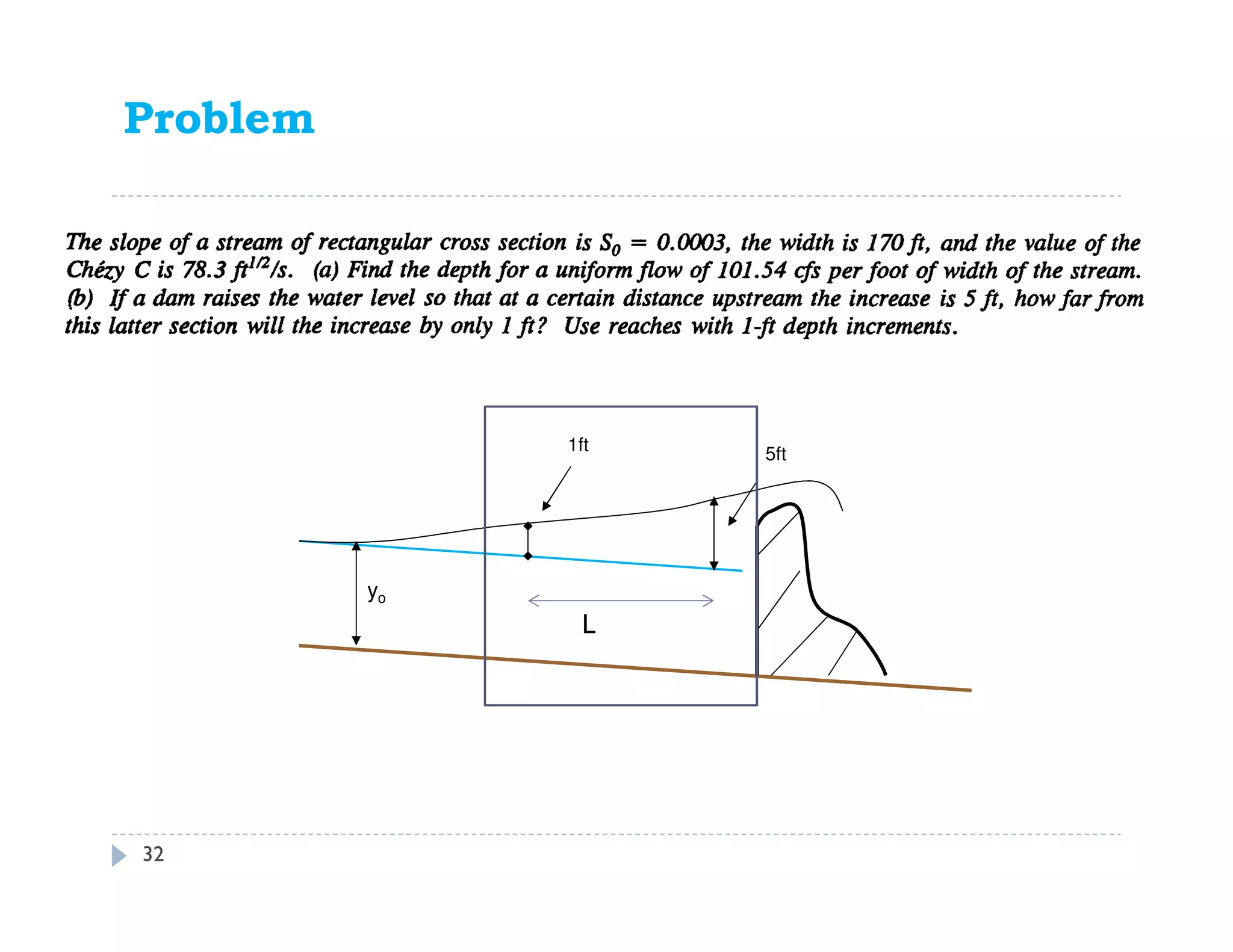
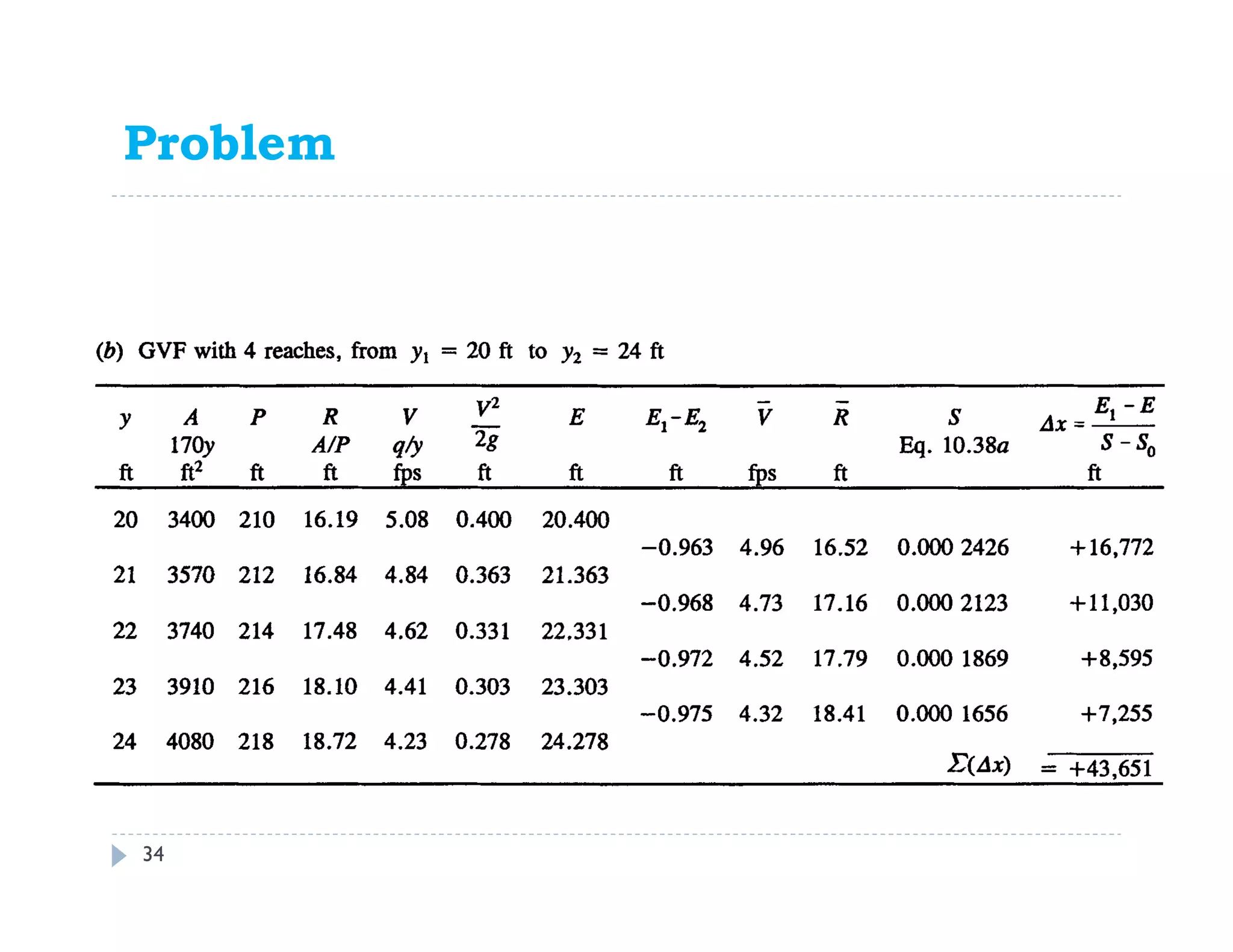
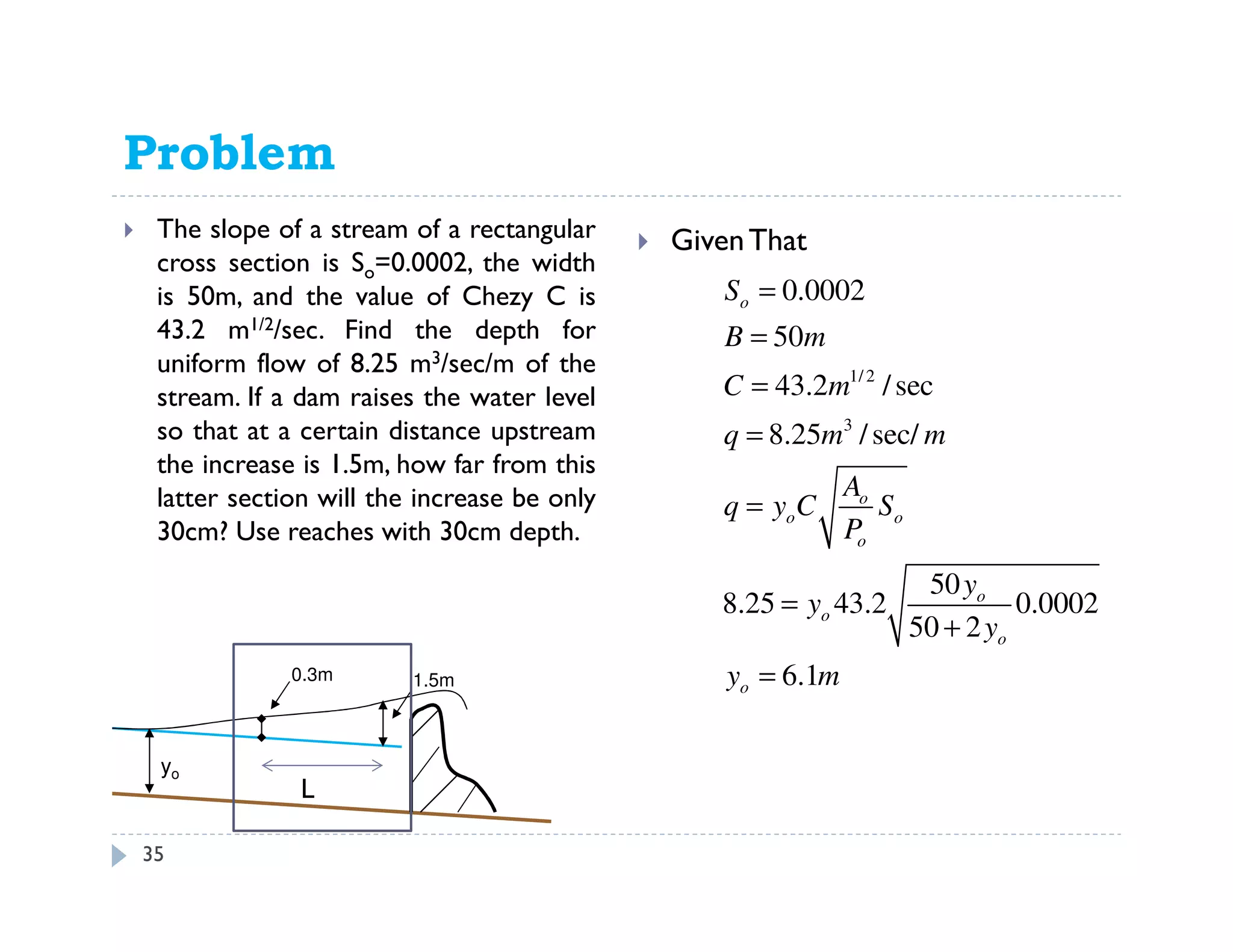
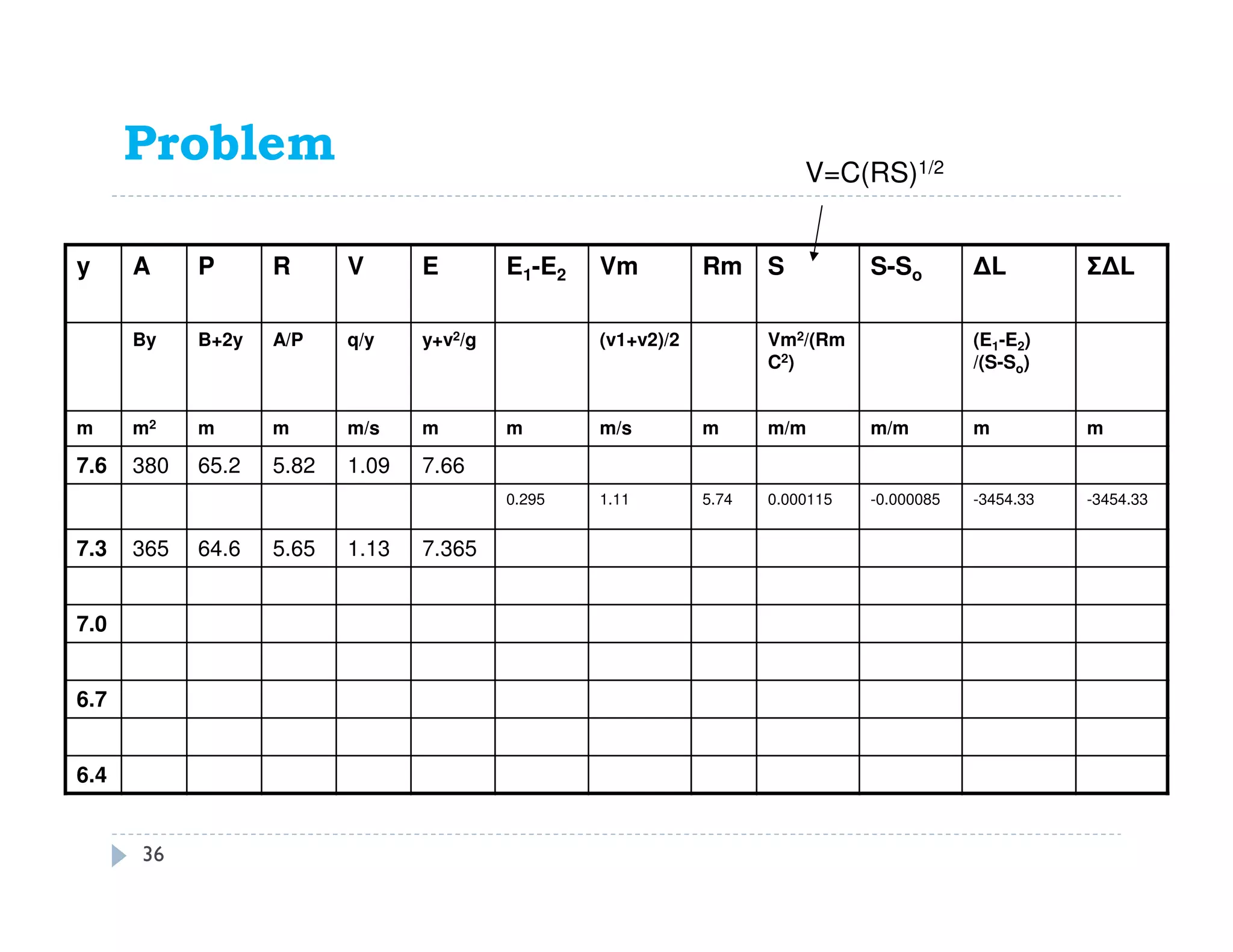
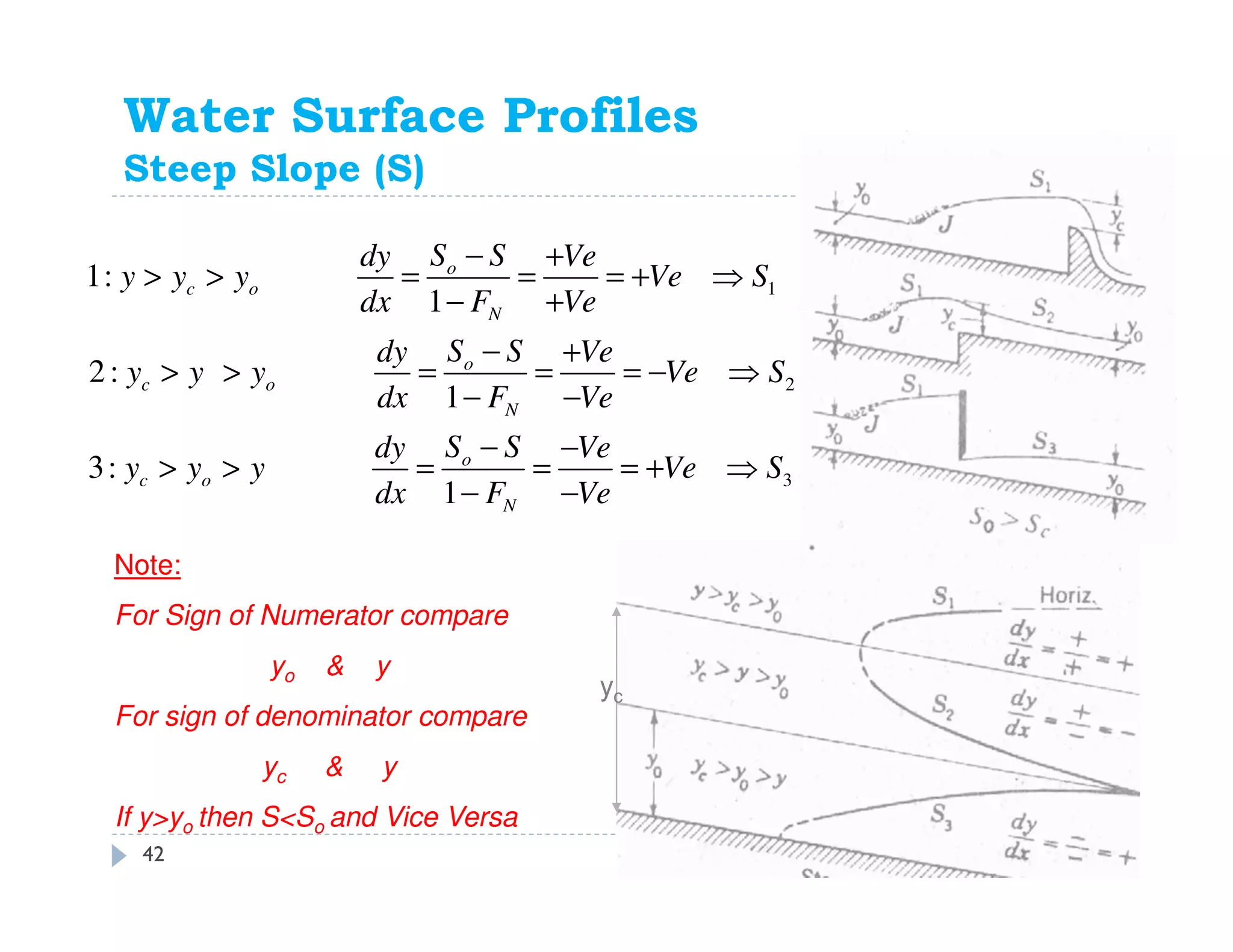
This document discusses open channel hydraulics and specific energy. It defines key terms like head, energy, hydraulic grade line, energy line, critical depth, Froude number, specific energy, and gradually varied flow. It explains the concepts of critical depth, alternate depths, and how specific energy relates to critical depth for rectangular and non-rectangular channels. It also discusses surface profiles, backwater curves, types of bed slopes, occurrence of critical depth with changes in bed slope, and the energy equation for gradually varied flow. An example problem is included to demonstrate calculating distance between depths for gradually varied flow.

1. Open Channel Hydraulics
1
Hydraulics
Dr. Mohsin Siddique
Assistant Professor

2. Steady Flow in Open Channels
Specific Energy and Critical Depth
Surface Profiles and Backwater Curves in Channels of
Uniform sections
Hydraulics jump and its practical applications.
Flow over Humps and through Constrictions
Broad Crested Weirs andVenturi Flumes
2

3. Specific Energy and Critical Depth
Basic Definitions
Head
Energy per unit weight
Energy Line
Line joining the total head at different positions
Hydraulics Grade Line
Line joining the pressure head at different positions
3

4. Specific Energy and Critical Depth
Basic Definitions
Open Channel Flow
1Z
g
V
2
2
1
Datum
So
1y
2Z
g
V
2
2
2
2y
HGL
EL
Water Level
lh
g
V
yZ
g
V
yZ +++=++
22
2
2
22
2
1
11
4

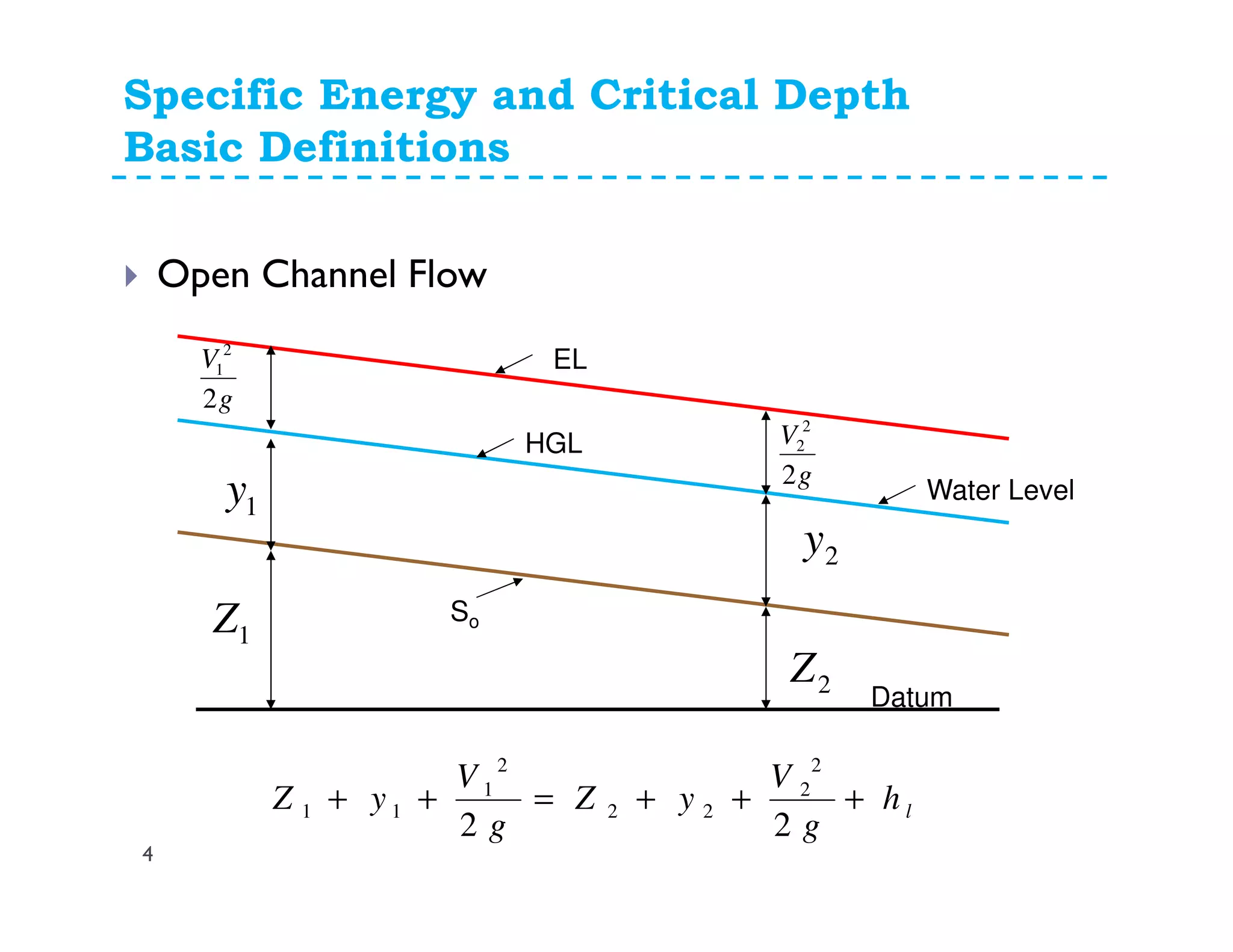
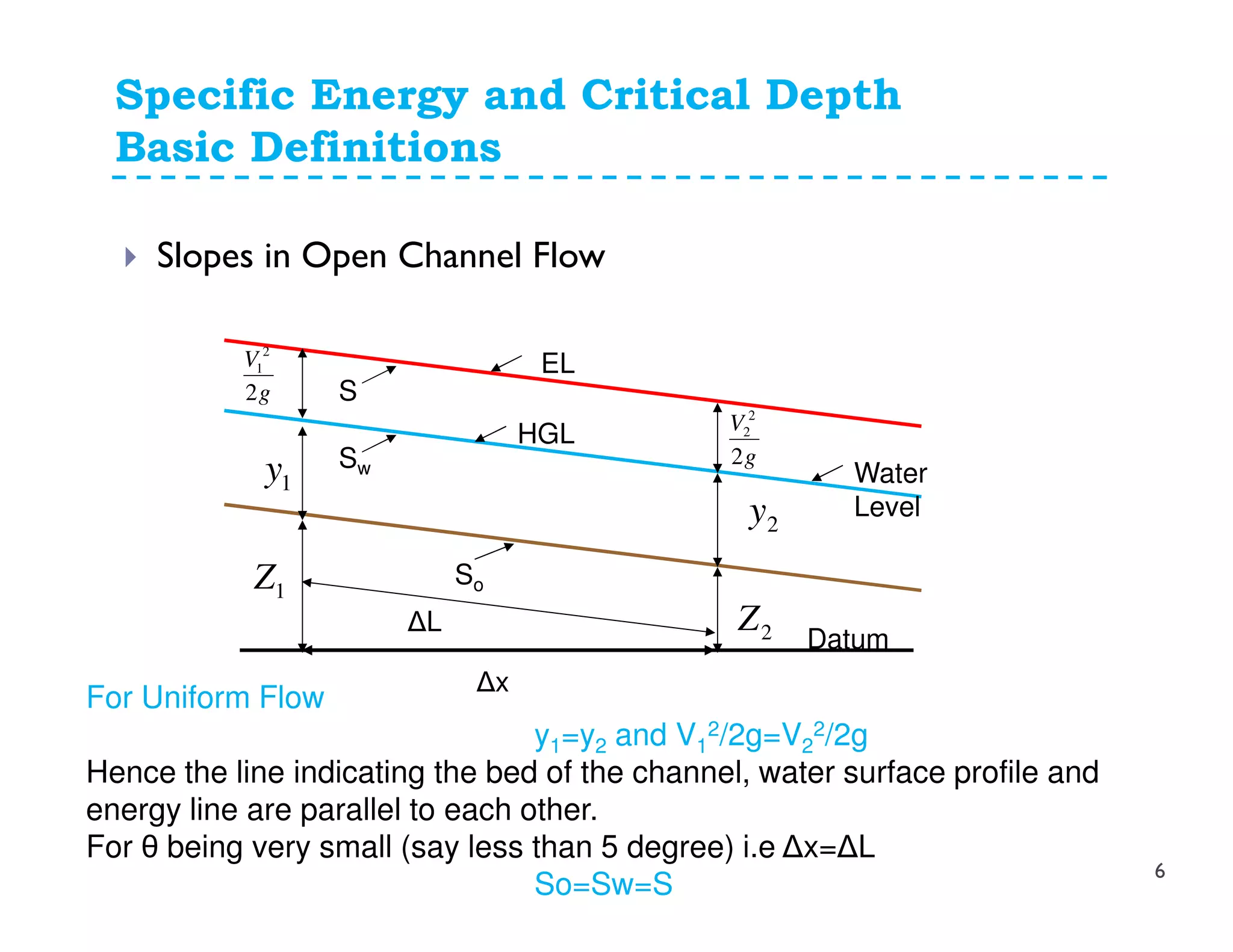
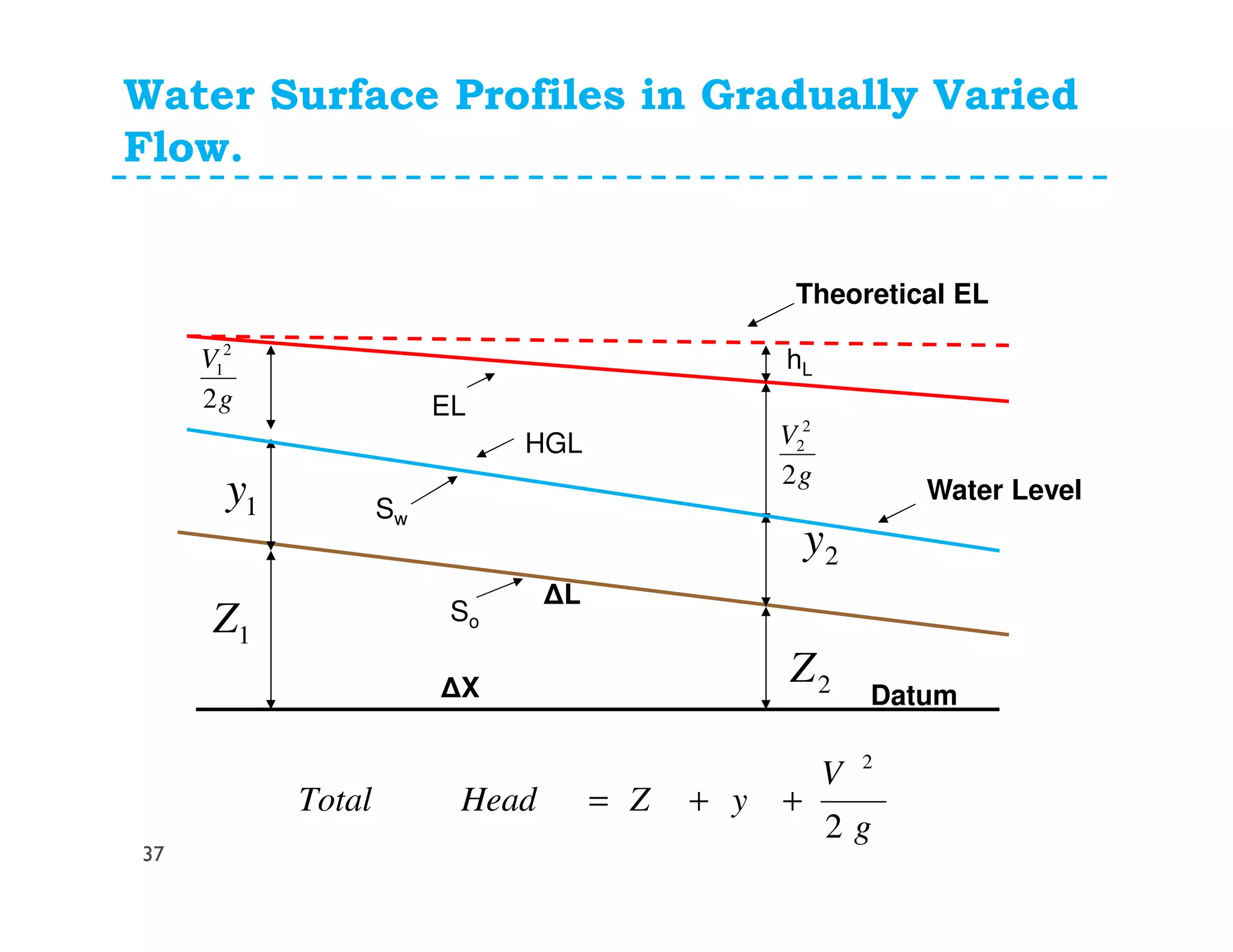
5. Slopes in Open Channel Flow
So= Slope of Channel Bed = (Z1-Z2)/(Δx)= -ΔZ/Δx
Sw= Slope of Water Surface= [(Z1+y1)-(Z2+y2)]/Δx
S= Slope of Energy Line= [(Z1+y1+V1
2/2g)-(Z2+y2+V2
2/2g)]/Δx
= hl/ΔL
1Z
g
V
2
2
1
Datum
So
1y
2Z
g
V
2
2
2
2y
HGL
EL
Water
Level
Sw
S
∆L
∆x
Specific Energy and Critical Depth
Basic Definitions
5

6. Specific Energy and Critical Depth
Basic Definitions
Slopes in Open Channel Flow
1Z
g
V
2
2
1
Datum
So
1y
2Z
g
V
2
2
2
2y
HGL
EL
Water
Level
Sw
S
∆L
∆x
For Uniform Flow
y1=y2 and V1
2/2g=V2
2/2g
Hence the line indicating the bed of the channel, water surface profile and
energy line are parallel to each other.
For θ being very small (say less than 5 degree) i.e ∆x=∆L
So=Sw=S
6

7. Specific Energy and Critical Depth
Basic Definitions
Froude’s Number (FN)
It is the ratio of inertial forces to
gravitational forces.
For a rectangular channel it may be
written as
FN= 1 Critical Flow
> 1 Super-Critical Flow
< 1 Sub-Critical Flow
gy
V
NF =
William Froude (1810-79)
Born in England and engaged
in shipbuilding. In his sixties
started the study of ship
resistance, building a boat
testing pool (approximately 75
m long) near his home. After his
death, this study was continued
by his son, Robert Edmund
Froude (1846-1924). For
similarity under conditions of
inertial and gravitational forces,
the non-dimensional number
used carries his name.
7

8. Specific Energy and Critical Depth
(Rectangular Channels)
Specific Energy
Specific Energy at a section in an open channel is the energy
with reference to the bed of the channel.
Mathematically;
Specific Energy = E = y+V2/2g
For a rectangular Channel
q = Discharge per unit width m3/s per m
B
( ) Vy
B
VBy
B
AV
B
Q
qwhere
yE
yE
yg
q
g
V
====
+=
+=
2
2
2
2
2 y
8
Datum

9. Specific Energy and Critical Depth
As it is clear from E~y diagram
drawn for constant discharge for
any given value of E, there would
be two possible depths, say y1 and
y2. These two depths are called
Alternate depths.
However for point C
corresponding to minimum
specific energy Emin, there would
be only one possible depth yc. The
depth yc is know as critical depth.
The critical depth may be defined
as depth corresponding to minimum
specific energy discharge remaining
Constant.
E~y Diagram or E-Diagram
Static Head
Line
BQqwhereyE yg
q
/2
2
2
=+=
9

10. Specific Energy and Critical Depth
For y>yc ,V<Vc Deep Channel
Sub-Critical Flow,Tranquil Flow, Slow Flow.
For y<yc ,V>Vc Shallow Channel
Super-Critical Flow, Shooting Flow, Rapid Flow, Fast Flow.
10

11. Specific Energy and Critical Depth
Relationship Between Critical Depth and Specific Energy
for rectangular channels
22
2
cc y
g
V
=
Substituting in eq. (1)
( )
( )
( )
( )g
yVc
g
yV
c
ccg
yV
c
g
q
c
cg
q
c
gy
q
dy
dE
gy
q
dy
dE
gy
q
g
V
cc
cc
cc
y
y
yVqy
y
yyy
yyE
2
3
3
3/1
3/1
23
3
2
32
22
2
2
2
22
22
22
2
2
2
2
)2(
)(
01
1
)1(
=
=
==
=
==
=−=
−=
+=+=
Q
Q
)5(2
3
2min
cc
y
cc
yE
yEE c
=
+==
11
)4(1
)3(22
2
=
=
c
c
c
gy
V
y
g
Vc
Froude #
=1 !!

12. Example
12

13. Problem
13
( ) 3/12
g
q
cy =
( ) 2/1
cc gyV =
2/13/2486.1
oSAR
n
Q =

14. Problem 11.38
Water is released from a sluice gate in a rectangular channel 1.5m wide such
that depth is 0.6 m and velocity is 4.5 m/s. Find
(a). Critical Depth for this specific energy
(b). Critical Depth for this rate of Discharge
(c).The type of flow and alternate depth by either direct solution or the
discharge Curve.
Solution
B=1.5 m
y=0.6 m
V= 4.5 m/sec
(a)
mEy
m
g
V
yEnergySpecific
c 088.1
3
2
632.1
2
2
==
=+=
sluice gate
14
Critical flow

15. Problem 11.38
(b)
(c)
CriticalSuperisFlowTherefore
ym
g
q
y
mpermvyq
mByVAVQ
c
−
>=





=
==
===
906.0
sec/7.2
sec/05.4
3/12
3
CriticalSuperisFlow
gy
V
FN
−
>== 1855.1
2
2
2
2
3
)81.9(2
7.2
632.1
2
sec/05.4
y
y
gy
q
yE
mByVAVQ
+=
+=
===
my
my
yy
46.1
6.0
037156.0632.1 23
=
=
=+−
15

16. Specific Energy and Critical Depth
(Non Rectangular Channels)
Hydraulic Depth
The hydraulic depth, yh for non rectangular channel is the depth of a
rectangular channel having flow area and base width the same as the flow
area and top width respectively as for non rectangular channel.
dy
T
A y
dy
T
A yh
16

17. Specific Energy and Critical Depth
Relationship Between Critical Depth and Specific Energy
Froude’s number may be numerically
calculate as
3
2
2
2
2
gA
TQ
F
T
A
y
gA
Q
F
gy
V
F
N
h
T
A
h
N
N
=
==
=
ycy
g
Q
T
A
Therefore
dy
dE
flowCriticalfor
T
gA
Q
dy
dE
TdydASince
=






=
=
−=
=
23
3
2
0
1
17
dy
dA
gA
Q
dy
dE
gA
Q
yEEq
3
2
2
2
1
2
)1.(
−=
+=⇒

18. Problems11.45
A Trapezoidal canal with side slopes 1:2 has a bottom width of
3m and carries a flow of 20 m3/s.
a). Find the Critical Depth and Critical velocity.
b). If the canal is lined with Brick (n=0.015), find the critical slope for the
same rate of discharge.
Solution
B=3m
T
A= (B+xy)y
P= B+2y(1+x2)1/2
T= B+2xy
1
x
Q=20 m3/s
x= 2
18

19. Problem 11.45
Q2/g = A3/T
(b)
Q2/g y A T A3/T
40.775 1 5 7 17.85
2 14 11 249.45
1.2 6.48 7.8 34.88
1.25 6.883 8.004 40.74
1.2512 6.885 8.0048 40.77
224433.0
2/1
2/3
=






=
cS
S
P
A
n
A
Q
19

20. Problem
The 50o triangular channel in Fig. E10.6 has a flow rate Q
16 m3/s. Compute (a) yc, (b)Vc, and (c) Sc if n 0.018.
Answer: (a). 2.37m, (b). 3.41m, (c ) 0.00542
20
20

21. Surface Profiles and
Backwater Curves in Channels of
Uniform sections
21

22. Steady Flow in Open Channels
Specific Energy and Critical Depth
Surface Profiles and Backwater Curves in Channels of
Uniform Sections
Hydraulics jump and its practical applications.
Flow over Humps and through Constrictions
Broad Crested Weirs andVenturi Flumes
22

23. Types of Bed Slopes
Mild Slope (M)
yo > yc
So < Sc
Critical Slope (C)
yo = yc
So = Sc
Steep Slope (S)
yo < yc
So > Sc
So1<Sc
So2>Sc
yo1
yo2
yc
Break
23
yo= normal depth of flow
yc= critical depth
So= channel bed slope
Sc=critical channel bed slope

24. Occurrence of Critical Depth
Change in Bed Slope
Sub-critical to Super-Critical
Control Section
Super-Critical to Sub-Critical
Hydraulics Jump
Control Section
So1<Sc
So2>Sc
yo1
yo2
yc
Break where
Slope changes
Dropdown Curve
So1>Sc
So2<Sc
yo1
yo2
yc
Hydraulic Jump
24

25. Occurrence of Critical Depth
Change in Bed Slope
Free outfall
Mild Slope
Free Outfall
Steep Slope
yb~ 0.72 yc
So<Sc
yo
yc
3~10 yc
Brink
yc
So>Sc
25

26. Non Uniform Flow or Varied Flow.
For uniform flow through open
channel, dy/dl is equal to zero.
However for non-uniform flow the
gravity force and frictional
resistance are not in balance. Thus
dy/dl is not equal to zero which
results in non-uniform flow.
There are two types of non
uniform flows.
In one the changing condition
extends over a long distance and
this is called gradually varied flow.
In the other the change may occur
over very abruptly and the transition
is thus confined to a short distance.
This may be designated as a local
non-uniform flow phenomenon or
rapidly varied flow.
So1<Sc
So2>Sc
yo1
yo2
yc
Break
26

27. Energy Equation for Gradually Varied Flow.
1Z
g
V
2
2
1
Datum
So
1y
2Z
g
V
2
2
2
2y
HGL
EL
Water Level
lh
g
V
yZ
g
V
yZ +++=++
22
2
2
22
2
1
11
Theoretical EL
Sw
hL
∆X
∆ L
S
27
Remember: Both sections are subject to atmospheric pressure

28. Energy Equation for Gradually Varied Flow.
( )
( ) ( )
profilesurfacewateroflengthLWhere
SS
EE
L
LSLSEE
Now
for
L
ZZ
X
ZZ
S
L
h
S
hZZ
g
V
y
g
V
y
o
o
o
o
L
L
=∆
−
−
=∆
∆+∆−=
<
∆
−
≈
∆
−
=
∆
=
+−−+=+
)1(
6,
22
21
21
2121
21
2
2
2
2
1
1
θ
An approximate analysis of gradually varied, non uniform flow can
be achieved by considering a length of stream consisting of a
number of successive reaches, in each of which uniform occurs.
Greater accuracy results from smaller depth variation in each reach.
28

29. Energy Equation for Gradually Varied Flow.
3/4
22
2/13/21
m
m
mm
R
nV
S
SR
n
V
=
=
The Manning's formula (or Chezy’s formula) is applied to average
conditions in each reach to provide an estimate of the value of S for that
reach as follows;
2
2
21
21
RR
R
VV
V
m
m
+
=
+
=
In practical, depth range of the interest is divided into small increments,
usually equal, which define the reaches whose lengths can be found by
equation (1)
29

30. Problem 11.59
A rectangular flume of planer
timber (n=0.012) is 1.5 m wide
and carries 1.7m3/s of water. The
bed slope is 0.0006, and at a
certain section the depth is 0.9m.
Find the distance (in one reach) to
the section where depth is 0.75m.
Is the distance upstream or
downstream ?
3
1
2
Rectangular Channel
0.012
1.5
1.7 /sec
0.0006
0.9
0.75
o
n
B m
Q m
S
y m
y
=
=
=
=
=
=
B
y
30

31. Problem 11.59
Solution
1 2
2 2
4/3
2
1
2
2
1
2
1 1 1
2 2 2
1 1
2 2
&
1.5 0.9 1.35
1.5 0.75 1.125
1.5 2 0.9 3.3
1.5 2 0.75 3
/ 0.41
/ 0.375
/ 1.26 / sec
/ 1.51 / sec
o
m
m
Since
E E
L
S S
V n
S
R
A x m
A x m
P x m
P x m
R A P
R A P
V Q A m
V Q A m
−
∆ =
−
=
= =
= =
= + =
= + =
= =
= =
= =
= =
2 2
4/3
1 2
2 2
1 2
1 2
0.3925
1.385
& 0.000961
2 2
317.73
m
m
m
m
o
o
R m
V m
V n
S
R
E E
Now L
S S
V V
y y
g g
L
S S
m Downstream
=
=
= =
−
∆ =
−
   
+ − +   
   ∆ =
−
=
31
upstream

32. Problem
32
5ft
yo
1ft
L

33. Problem
33

34. Problem
34

35. Problem 11.66
The slope of a stream of a rectangular
cross section is So=0.0002, the width
is 50m, and the value of Chezy C is
43.2 m1/2/sec. Find the depth for
uniform flow of 8.25 m3/sec/m of the
stream. If a dam raises the water level
so that at a certain distance upstream
the increase is 1.5m, how far from this
latter section will the increase be only
30cm? Use reaches with 30cm depth.
GivenThat
1.5m
yo
0.3m
1/ 2
3
0.0002
50
43.2 /sec
8.25 /sec/
50
8.25 43.2 0.0002
50 2
6.1
o
o
o o
o
o
o
o
o
S
B m
C m
q m m
A
q y C S
P
y
y
y
y m
=
=
=
=
=
=
+
=
L
35

36. Problem 11.66
y A P R V E E1-E2 Vm Rm S S-So ∆L Σ∆L
By B+2y A/P q/y y+v2/g (v1+v2)/2 Vm2/(Rm
C2)
(E1-E2)
/(S-So)
m m2 m m m/s m m m/s m m/m m/m m m
7.6 380 65.2 5.82 1.09 7.66
0.295 1.11 5.74 0.000115 -0.000085 -3454.33 -3454.33
7.3 365 64.6 5.65 1.13 7.365
7.0
6.7
6.4
V=C(RS)1/2
36

37. Water Surface Profiles in Gradually Varied
Flow.
1Z
g
V
2
2
1
Datum
So
1y
2Z
g
V
2
2
2
2y
HGL
EL
Water Level
g
V
yZHeadTotal
2
2
++=
Theoretical EL
Sw
hL
∆X
∆L
37

38. Water Surface Profiles in Gradually Varied
Flow.
( )
0
1
0
)2(
1
.
1
1
2
.tan..
22
2
2
3
2
2
3
2
2
2
2
22
1
=
−
−
∴
=
−
−
=
−
=−+−=−






−+=
−






++=
++=++=
N
o
N
NNo
F
SS
dx
dy
flowuniformFor
F
SSo
dx
dy
or
gsindecreaisflow
ofdirectionalongheadtotalthatshowssignve
gy
q
FF
dx
dy
SS
gy
q
dx
dy
dx
dZ
dx
dH
gulartanrecastionseccrossgConsiderin
gy
q
dx
d
dx
dy
dx
dZ
dx
dH
xdirectionhorizontalincedistrwHheadtotaltheatingDifferenti
gy
q
yZ
g
v
yZH
Q
Equation (2) is dynamic Equation for
gradually varied flow for constant value
of q and n
If dy/dx is +ve the depth of flow
increases in the direction of flow and
vice versa
38
Important assumption !!

39. Water Surface Profiles in Gradually Varied
Flow.
3/10
3/10
22
3/10
22
2/13/5
2/13/2
1
1






=∴
=
=
=
=
≈
y
y
S
S
y
qn
S
channel
gulartanrecinflowuniformFor
y
qn
S
orSy
n
q
orSy
n
V
yR
channelgulartanrecwideaFor
o
o
o
o
2
1 F
SS
dx
dy o
−
−
=
Consequently, for constant q and n,
when y>yo, S<So, and the numerator
is +ve.
Conversely, when y<yo, S>So, and
the numerator is –ve.
To investigate the denominator we
observe that,
if F=1, dy/dx=infinity;
if F>1, the denominator is -ve; and
if F<1, the denominator is +ve.
39

40. Classification of Surface Profiles
Mild Slope (M)
yo > yc
So < Sc
Critical Slope (C)
yo = yc
So = Sc
Steep Slope (S)
yo < yc
So > Sc
Horizontal (H)
So = 0
Adverse (A)
So = -ve
Type 1: If the stream
surface lies above both the
normal and critical depth of
flow (M1, S1)
Type 2: If the stream
surface lies between normal
and critical depth of flow
(M2, S2)
Type 3: If the stream
surface lies below both the
normal and critical depth of
flow. (M3, S3)
40

41. Water Surface Profiles
Mild Slope (M)
1
2
3
1:
1
2:
1
3:
1
o
o c
N
o
o c
N
o
o c
N
S Sdy Ve
y y y Ve M
dx F Ve
S Sdy Ve
y y y Ve M
dx F Ve
S Sdy Ve
y y y Ve M
dx F Ve
− +
> > = = = + ⇒
− +
− −
> > = = = − ⇒
− +
− −
> > = = = + ⇒
− −
yc
Note:
For Sign of Numerator compare
yo & y
For sign of denominator compare
yc & y
If y>yo then S<So and Vice Versa
41

42. Water Surface Profiles
Steep Slope (S)
1
2
3
1:
1
2:
1
3:
1
o
c o
N
o
c o
N
o
c o
N
S Sdy Ve
y y y Ve S
dx F Ve
S Sdy Ve
y y y Ve S
dx F Ve
S Sdy Ve
y y y Ve S
dx F Ve
− +
> > = = = + ⇒
− +
− +
> > = = = − ⇒
− −
− −
> > = = = + ⇒
− −
Note:
For Sign of Numerator compare
yo & y
For sign of denominator compare
yc & y
If y>yo then S<So and Vice Versa
yc
42

43. Water Surface Profiles
Critical (C)
1
3
1:
1
2:
1
o
o c
N
o
o c
N
S Sdy Ve
y y y Ve C
dx F Ve
S Sdy Ve
y y y Ve C
dx F Ve
− +
> = = = = + ⇒
− +
− −
= > = = = + ⇒
− −
Note:
For Sign of Numerator compare
yo & y
For sign of denominator compare
yc & y
If y>yo then S<So and Vice Versa
yo=yc
C2 is not possible
43

44. Water Surface Profiles
Horizontal (H)
( ) 2
( ) 3
1:
1
2:
1
o
o c
N
o
o c
N
S Sdy Ve
y y y Ve H
dx F Ve
S Sdy Ve
y y y Ve H
dx F Ve
∞
∞
− −
> > = = = − ⇒
− +
− −
> > = = = + ⇒
− −
Note:
For Sign of Numerator compare
yo & y
For sign of denominator compare
yc & y
If y>yo then S<So and Vice Versa
yc
H1 is not possible bcz water has to lower down
44

45. Water Surface Profiles
Adverse (A)
( ) 2
( ) 3
1:
1
2:
1
o
o c
N
o
o c
N
S Sdy Ve
y y y Ve A
dx F Ve
S Sdy Ve
y y y Ve A
dx F Ve
∞
∞
− −
> > = = = − ⇒
− +
− −
> > = = = + ⇒
− −
Note:
For Sign of Numerator compare
yo & y
For sign of denominator compare
yc & y
If y>yo then S<So and Vice Versa
yc
A1 is not possible bcz water has to lower down
45

46. Problem 1
46
Classify the water surface profile for given data,
Channel type: rectangular
n=0.013
B=1.6
So=0.0005, Q=1.7m
y= varies from 0.85-1.0m
Solution:
Calculate normal depth of flow yo using Manning’s equation
2
1 F
SS
dx
dy o
−
−
=
( ) 2/1
0
3/2
2/1
0
3/2
2
11
S
yB
By
By
n
SAR
n
Q
o
o
o 





+
==
y< yo

47. Problem 1
47
Determine Critical depth
Thus yo > yc slope is Mild and profile type will be one of M type
Since y lies between both yo and yc i.e. yo >y> yc, the profile type is M2
( ) m
g
q
yc 486.0
81.9
6.1/7.1
3/123/12
=







=





=

48. Problem 2
48
Classify the water surface profile for given data,
Channel type: rectangular
n=0.013
B=1.6
So=-0.0004 < 0 adverse slope
Q=1.7m
y= varies from 0.85-1.0m
Solution:
Calculate normal depth of flow yo:
2
1 F
SS
dx
dy o
−
−
=
yyo >∞=

49. Problem 2
49
Determine Critical depth
Thus yo > yc Since slope is Adverse and profile type will be one of A
type
Since y lies between both yo and yc i.e. yo >y> yc, the profile type is A2
( ) m
g
q
yc 486.0
81.9
6.1/7.1
3/123/12
=







=





=

50. Problem 3
50
B=15m, rectangular channel, Q=1400cfs, yo=6ft.
y=2.8m
Determine y to yo depth increase of decrease towards
downstream.
Solution: Determine yc
yo< yc mean So>Sc, Steep slope (S)
Now comparing all depths
yc > yo >y
Hence the slope type is S3
+=
+
+
=
−
−
= 2
1 F
SS
dx
dy o
Water depth will increase

51. Practice problems
51

52. Thank you
Questions….
Feel free to contact:
52