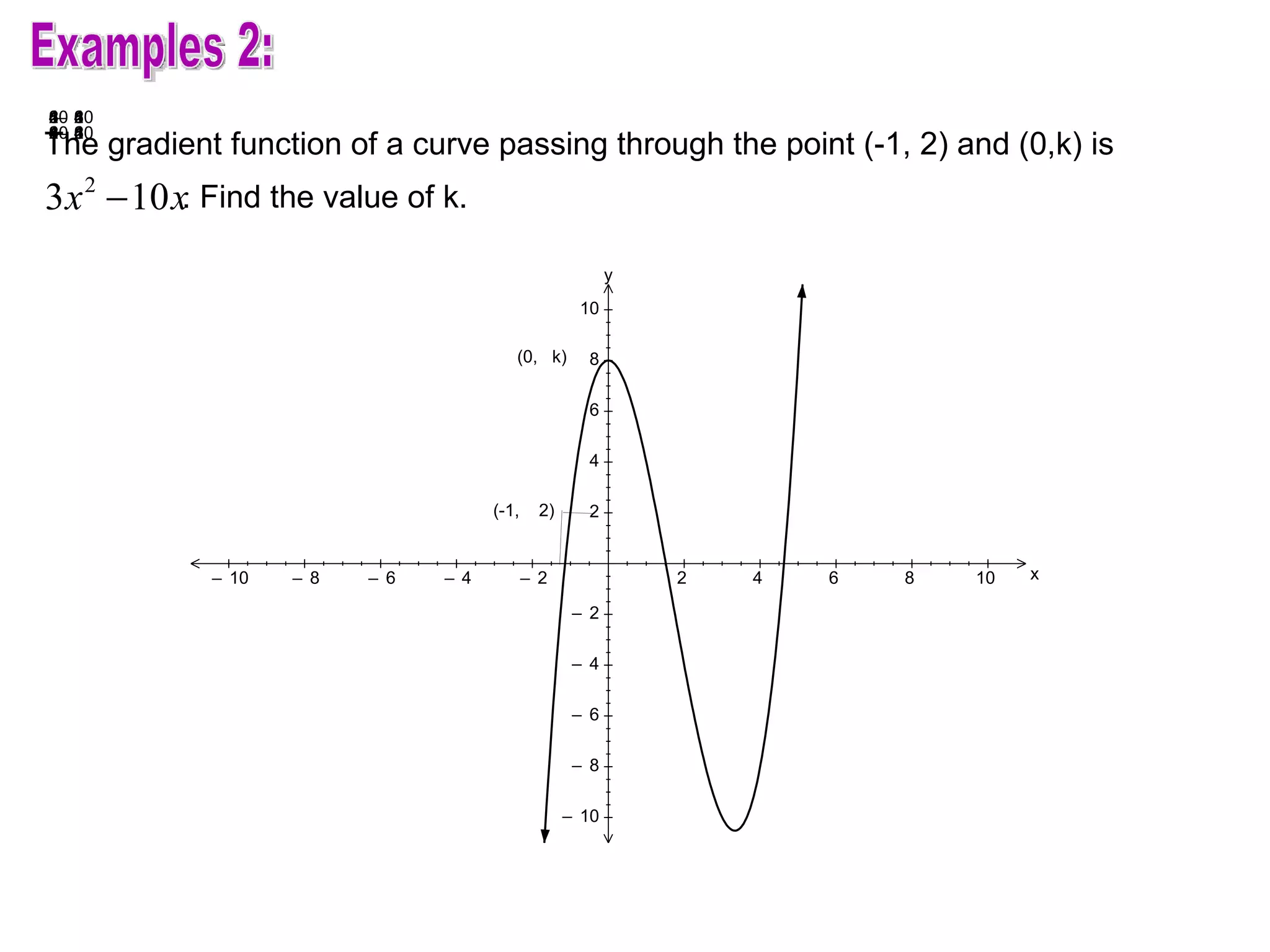
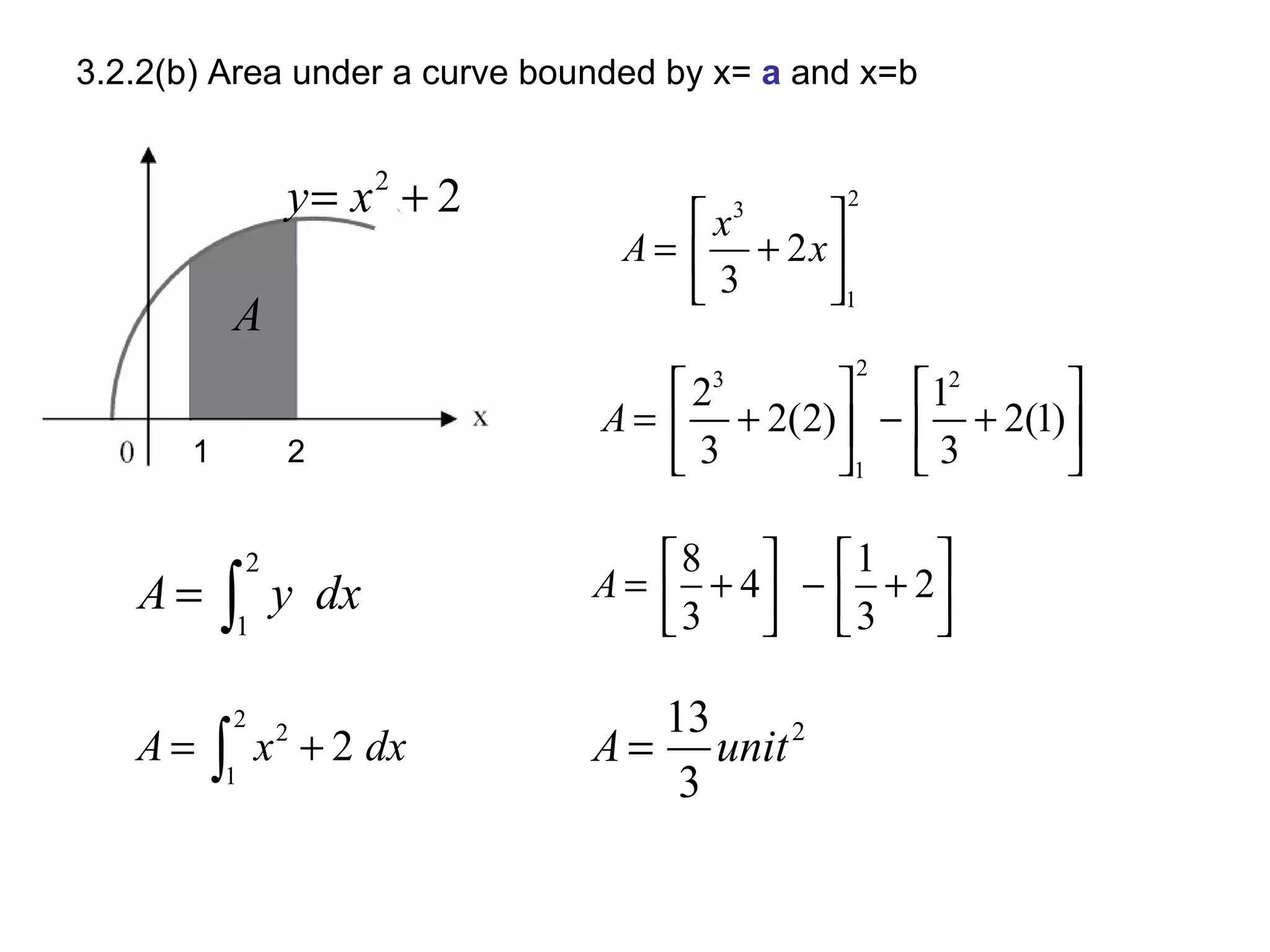
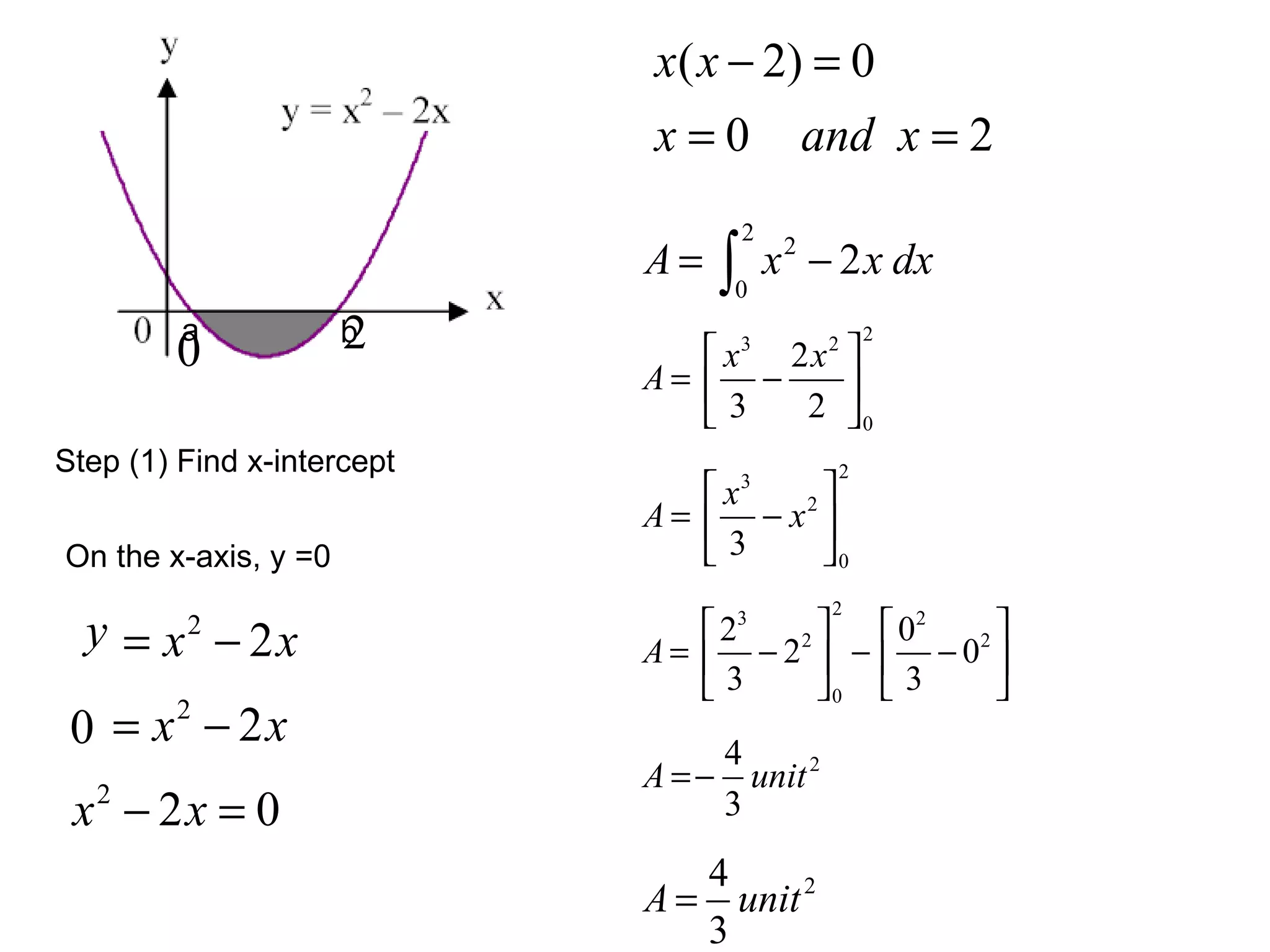
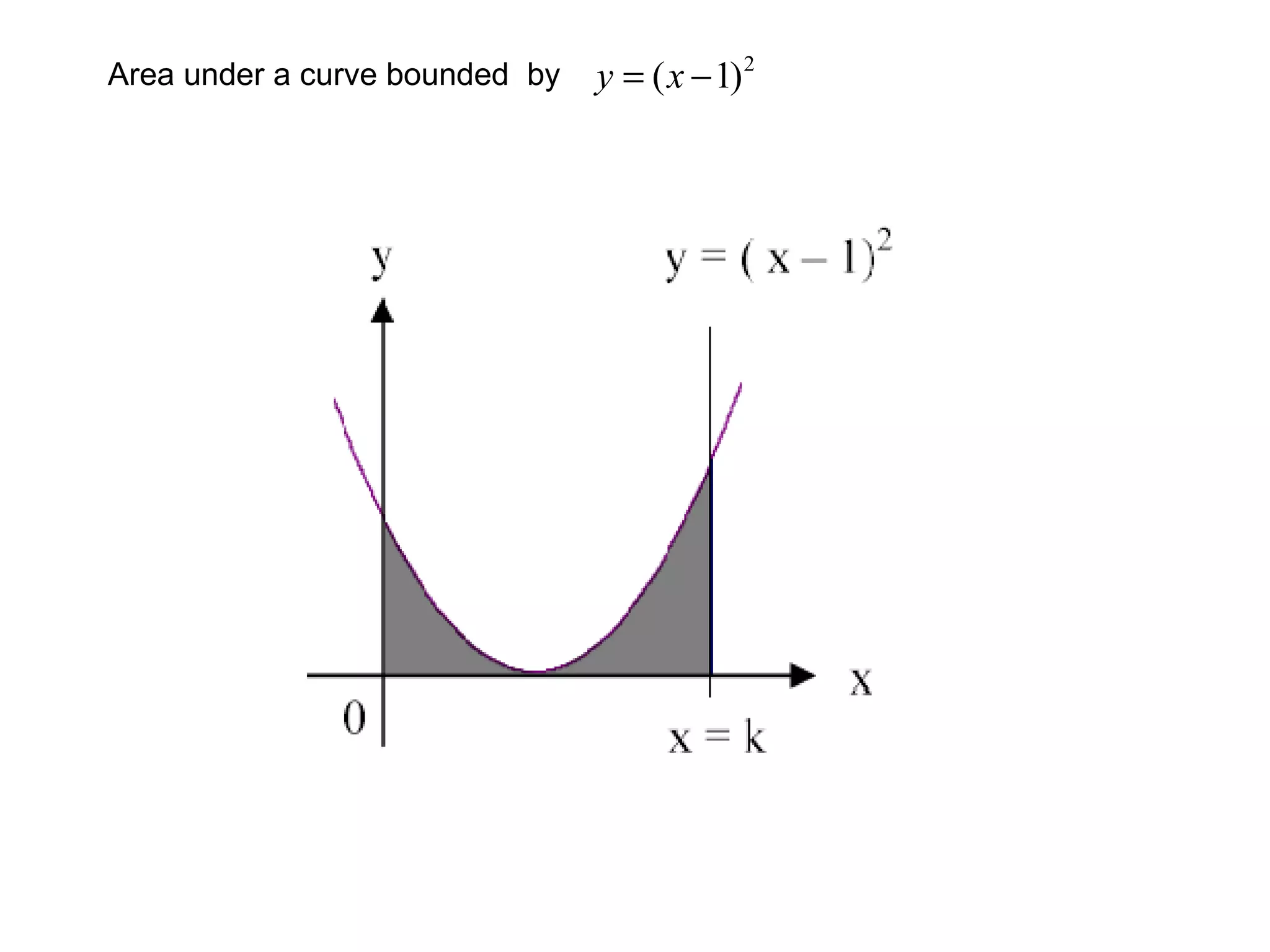
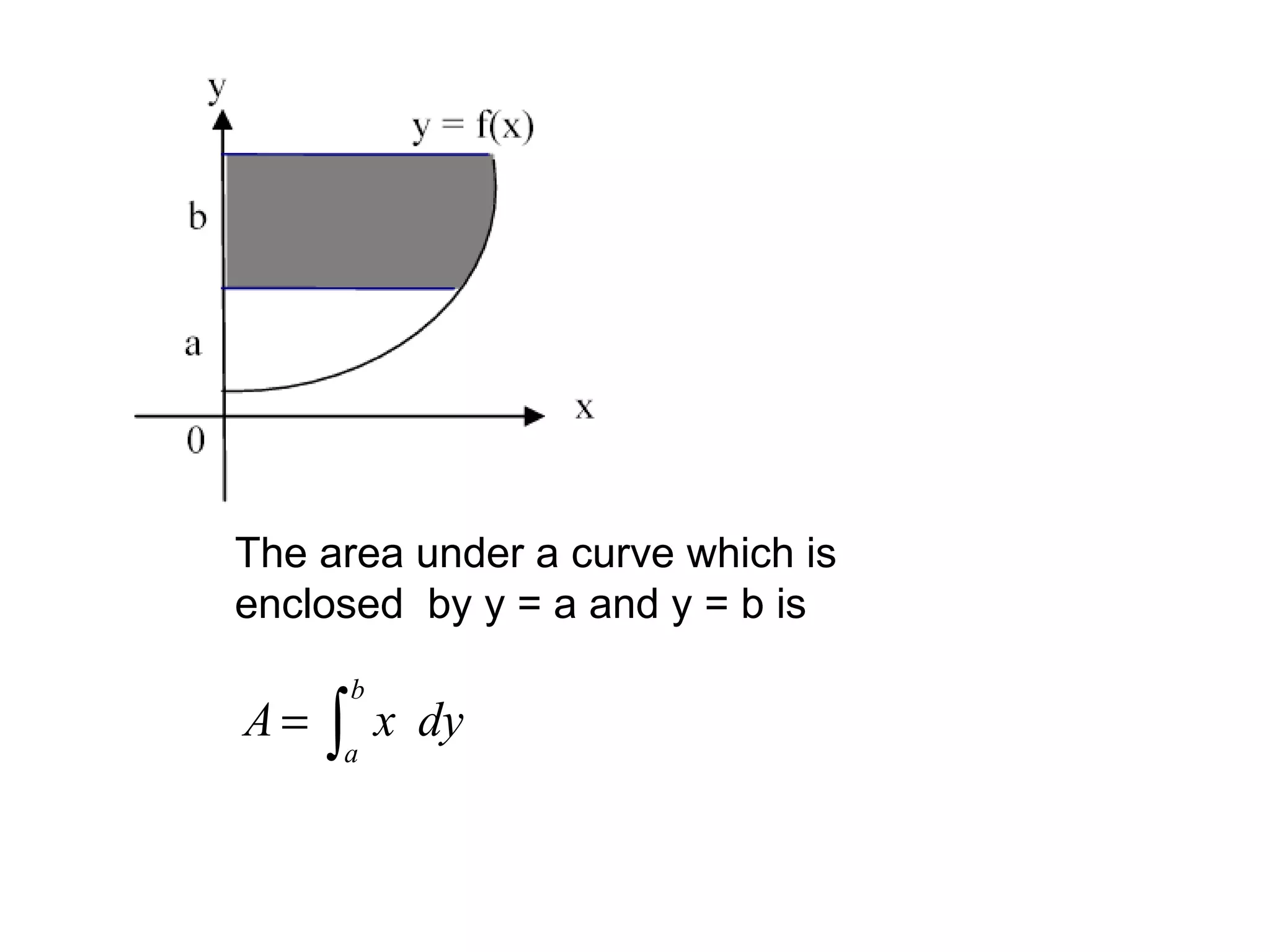
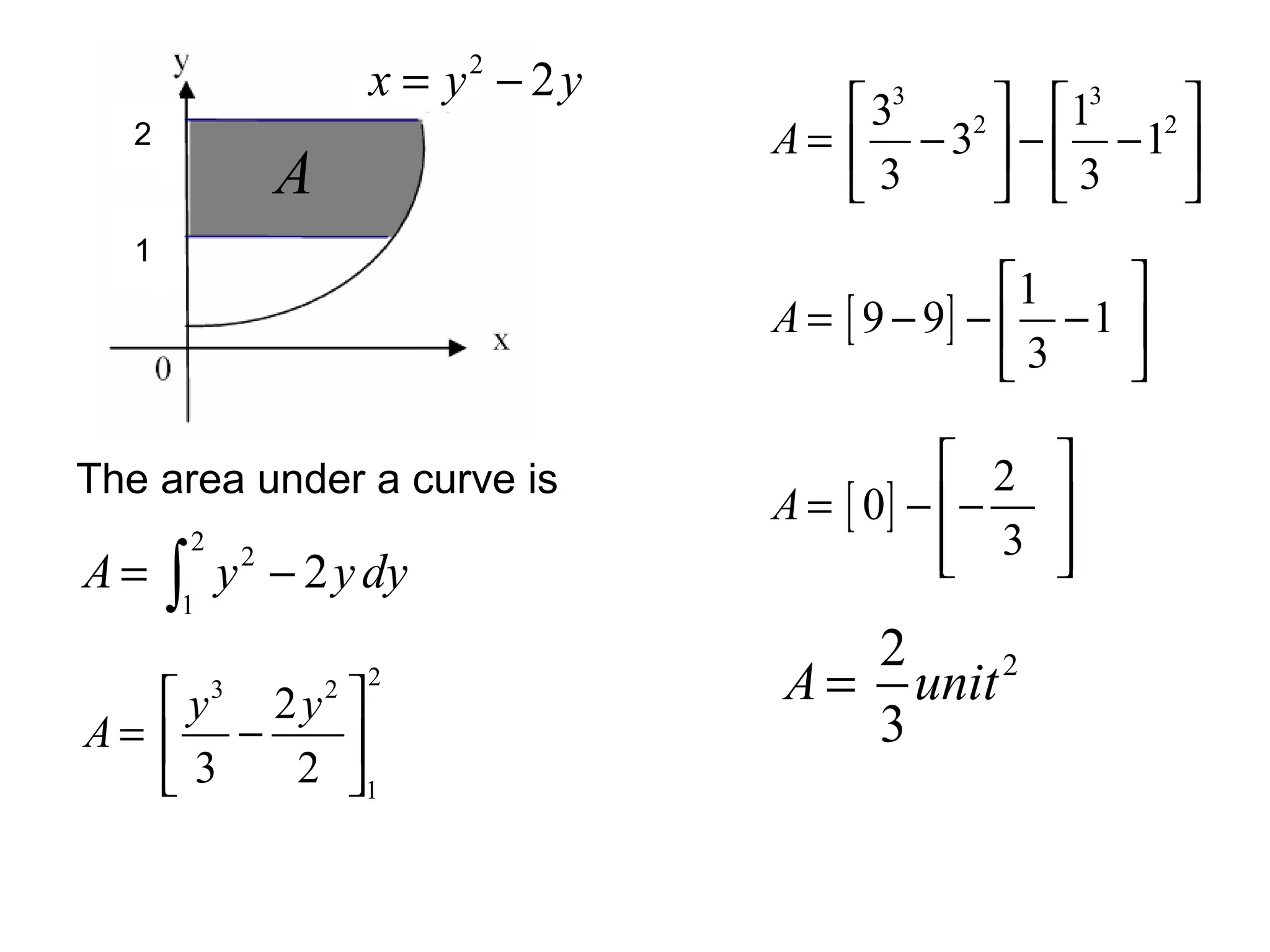
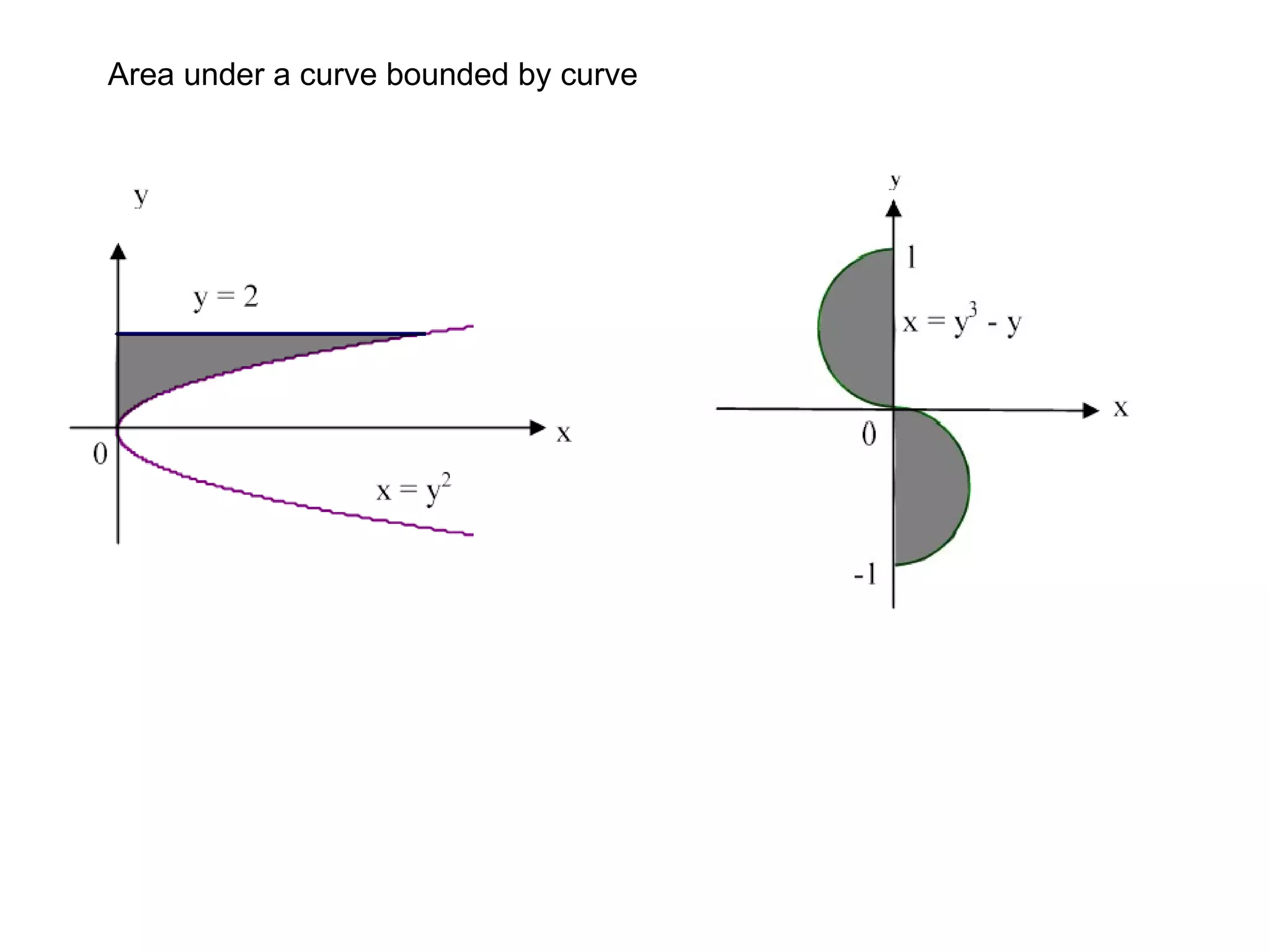
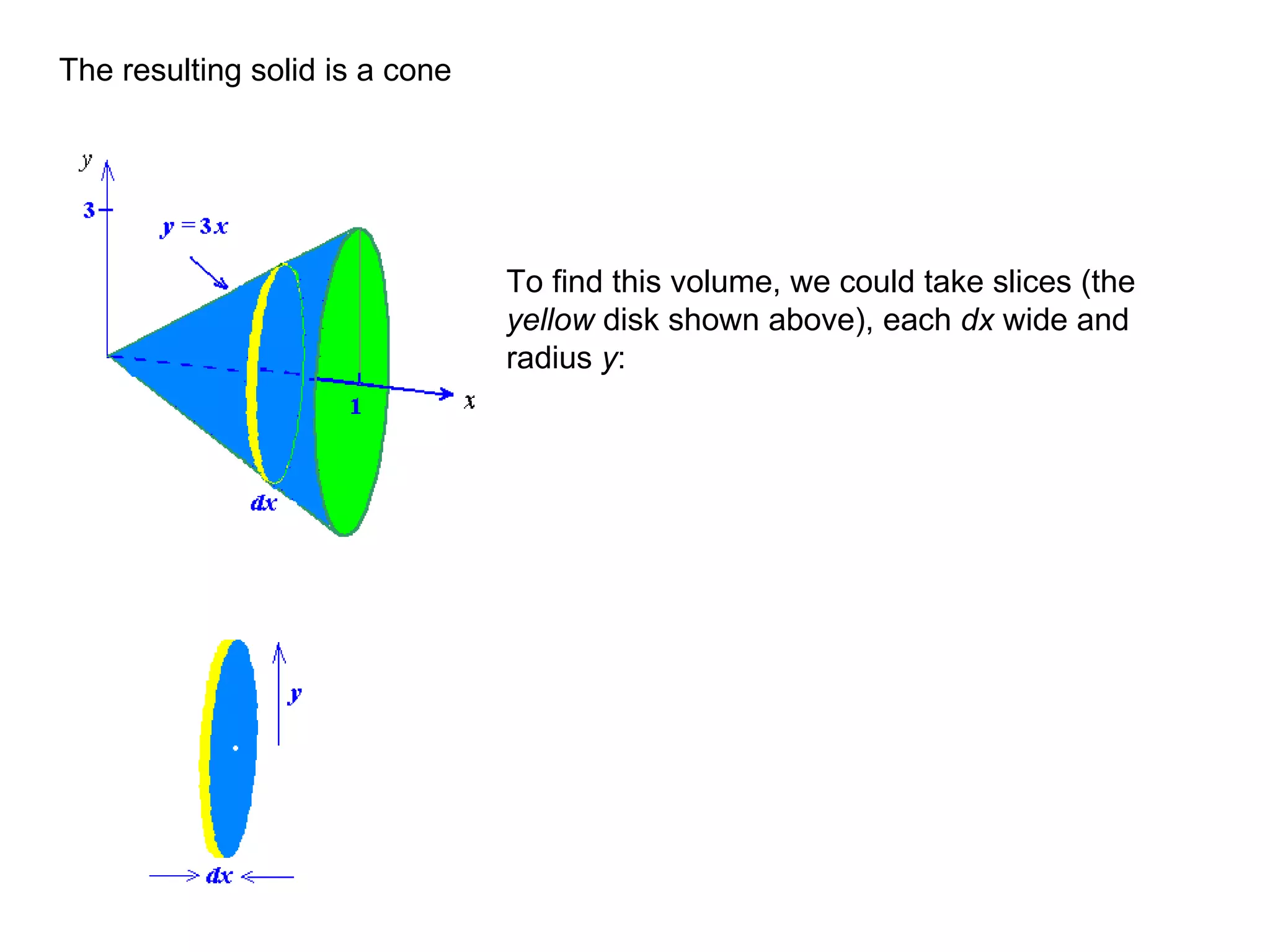
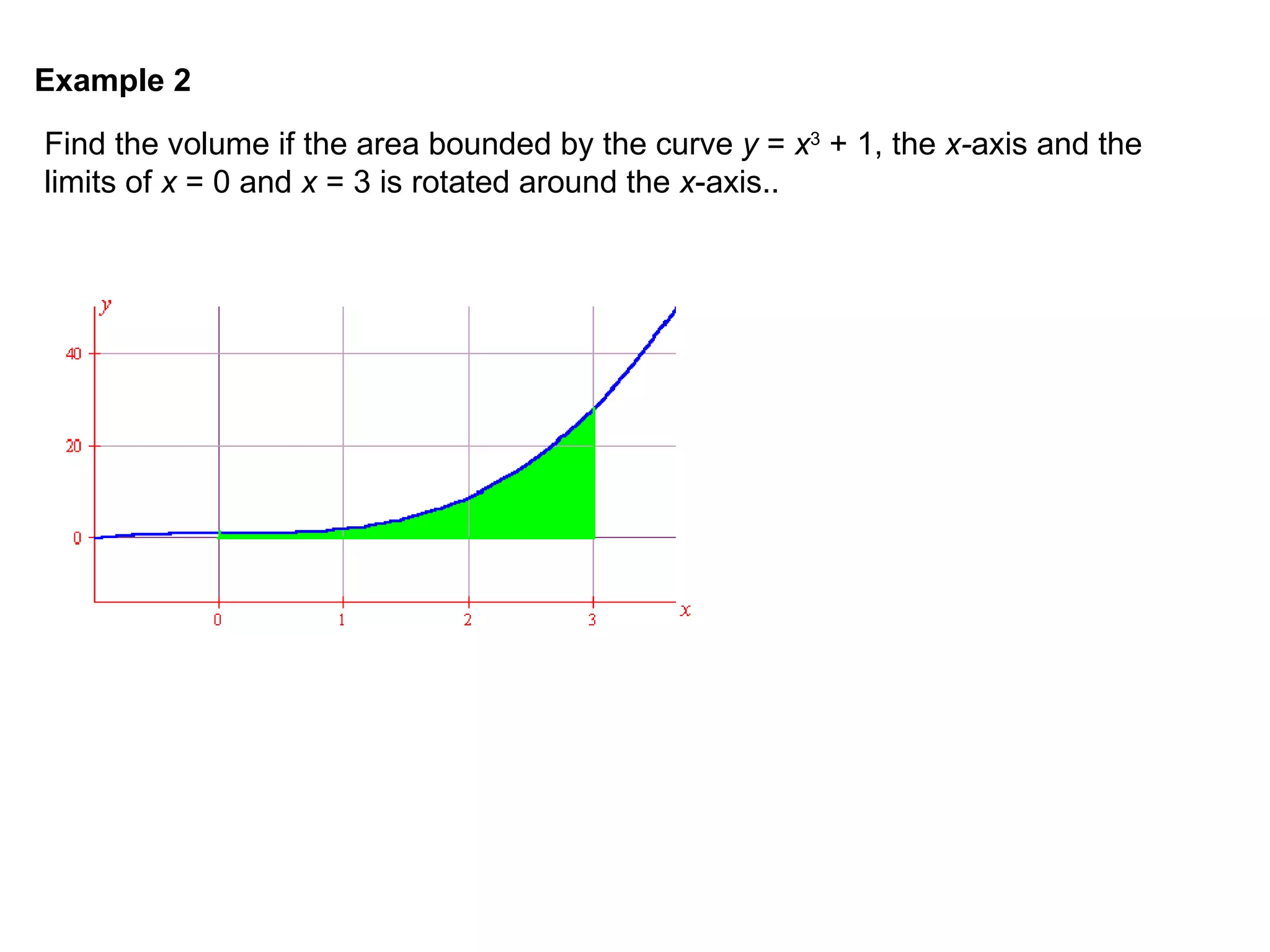
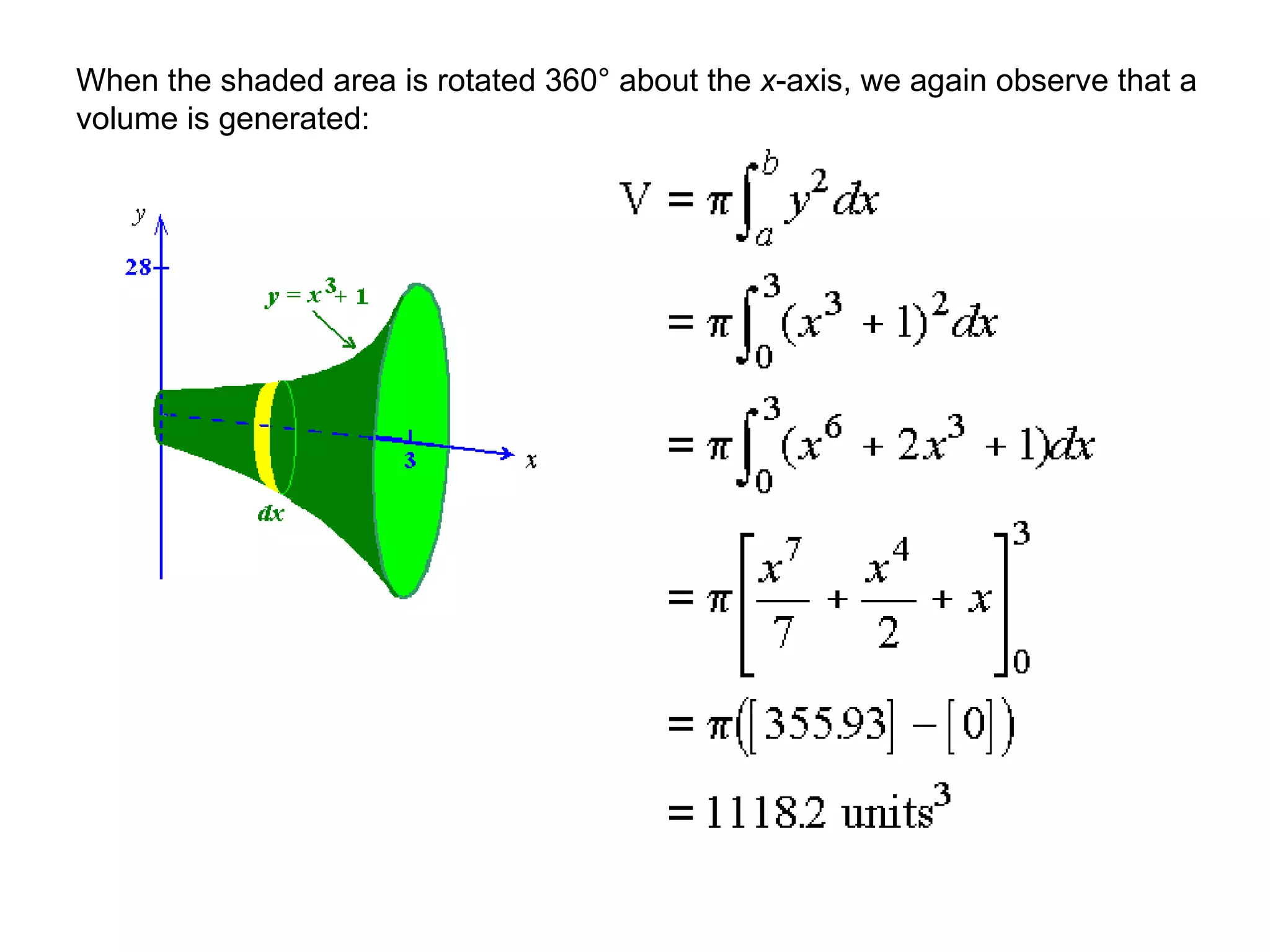
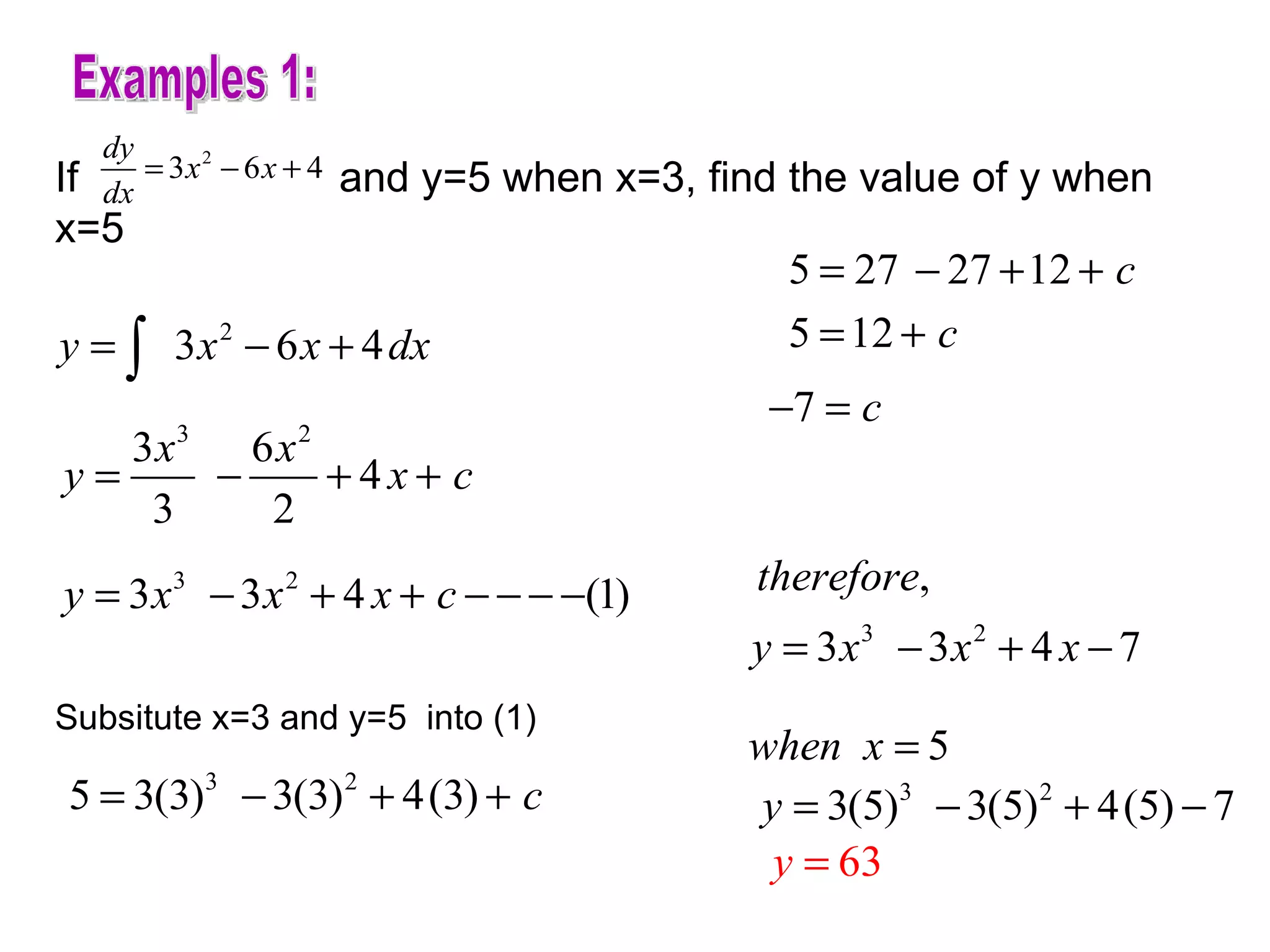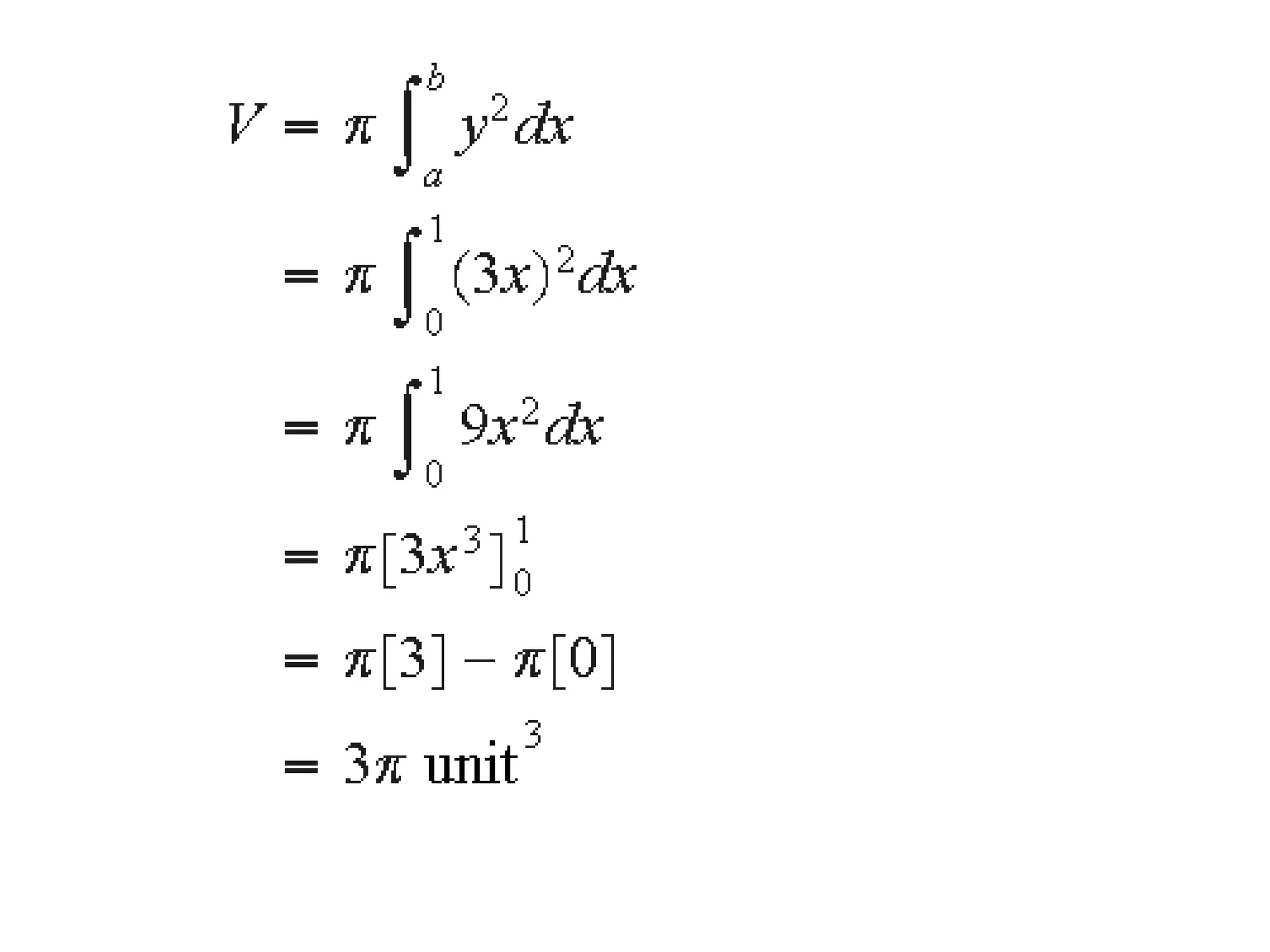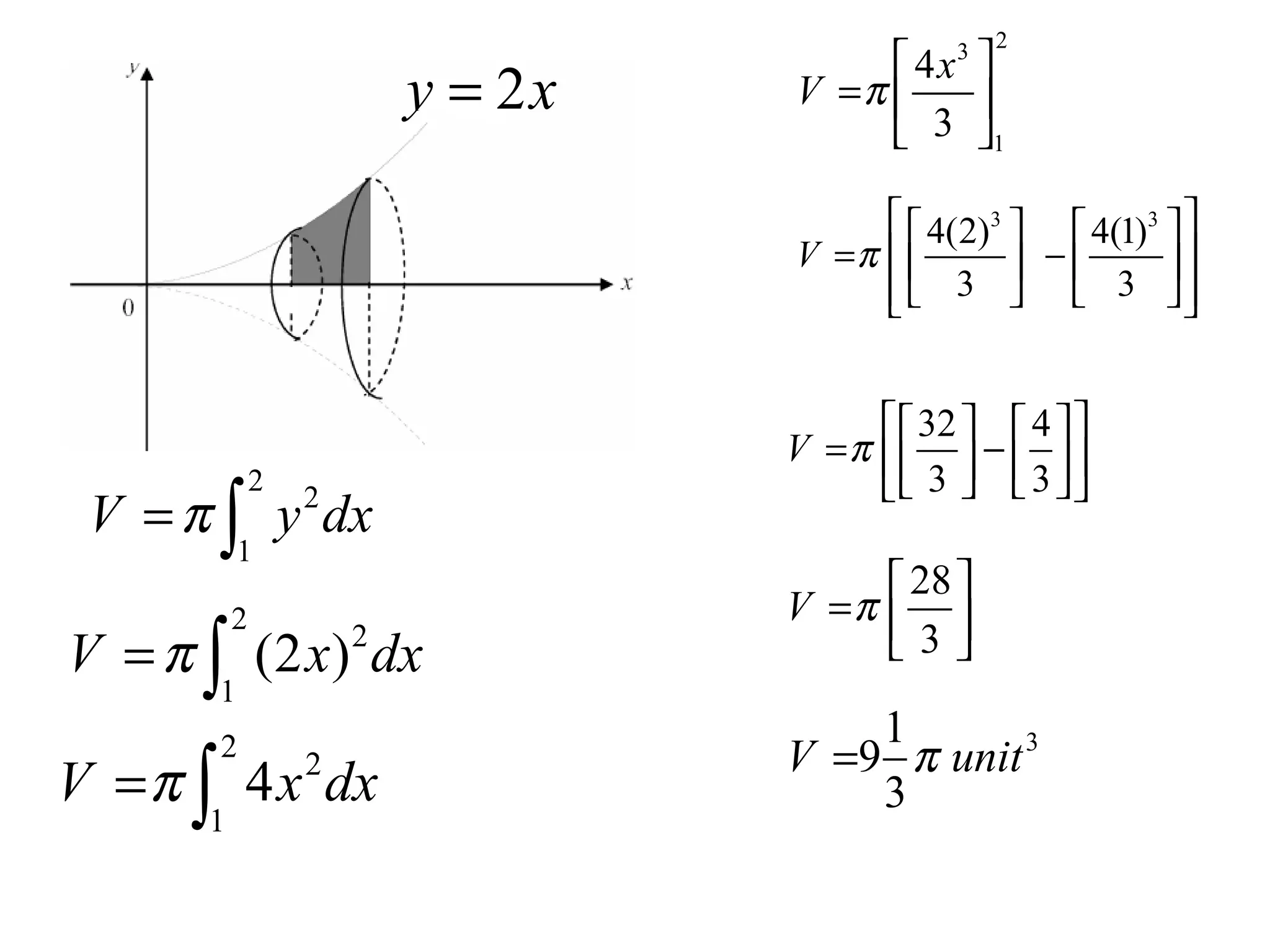The document discusses integration and indefinite integrals. It covers determining integrals by reversing differentiation, integrating algebraic expressions like constants, variables, and polynomials. It also discusses determining the constant of integration and using integration to find equations of curves from their gradients. Examples are provided to illustrate integrating functions and finding volumes generated by rotating an area about an axis.

1. Integration Learning Objectives : In this chapter, you will learn about the concept of indefinite integral Learning Outcomes: Determine integrals by reversing differentiation

2. 3.1 Indefinite Integral

3. 3.1.2 Integration of algebraic expressions Integrate (a) 8 (b) 3.5 (c) 3.1.2 (a) Integral of Constant

4. 3.1.2 Integration of algebraic expressions During differentiation, we carry out two operations on each term in x: multiply the term with the index, and reduce the index by 1. 3.1.2 (b) Integral of Differentiation Integration

5. Examples 1: Integrate each of the following with respect of x: (a) (b)

6. Examples 2: If the derivative of a function is given as find the function y.

7. 3.1.3 Determine the constant of Integration

8. Examples 1: Subsitute x=3 and y=5 into (1) If and y=5 when x=3, find the value of y when x=5

9. 3.1.4 Equations of curve from functions of gradients Examples 1: Find the equation of curve. by integration, The curve passing through the point (-1, 2) x=-1 when y=2 The equation of the curve is The gradient of a curve passing through the point (-1, 2) is given by

10. Examples 2: . Find the value of k. The gradient function of a curve passing through the point (-1, 2) and (0,k) is

11. The curve pass through (-1, 2) Therefore, the equation of the curve is At point (0, k),

12. Exercise 3-1-09 t0 6-1-09 Given that and that y=5 when x= -1, find the value of y when x=2 Given that and that v=2 when t = 1, find the value of v when t = 2.

13. 3.1.5 Integrate by substitution Find the integration by substitution

14. 3.1.5 Integrate by substitution Find the integration by substitution

15. 3.1.5 (a) Integral of

16. The gradient of the curve, Integrate with respect to x, we have Since the curve passes through (4, -3) The equation of the curve is The slope of a curve at any point P(x, y) is given by . Find the equation of the curve given that its passes through the point ( 4, -3)

17. Area under a curve

18. 3.2.2(b) Area under a curve bounded by x= a and x=b The area A under a curve by y = f(x) bounded by the x-axis from x=a to x=b is given by Integration as Summation of Area

19. 3.2.2(b) Area under a curve bounded by x= a and x=b 1 2

20. Step (1) Find x-intercept a b On the x-axis, y =0

21. Area under a curve bounded by

22. Area under a curve bounded by

23. The area under a curve which is enclosed by y = a and y = b is

24. The area under a curve is 1 2

25. Area under a curve bounded by curve

26. Area under a curve bounded

27. Exercise 19-2-09 23-2-09 1 2

28. Exercise Text Book Page 71 23-2-09 10- ( a) ( b ) ( c ) 11- ( a) ( b ) ( c ) 12- ( a) ( b )

29. Exercise Text Book Page 72 13- ( a) ( b ) ( c ) 14 17 ( a ) (b ) ( c )

30. Volume of Revolutions

31. The resulting solid is a cone To find this volume, we could take slices (the yellow disk shown above), each dx wide and radius y :

32. The volume of a cylinder is given by V = π r 2 h Because radius = r = y and each disk is dx high, we notice that the volume of each slice is: V = π y 2 dx Adding the volumes of the disks (with infinitely small dx ), we obtain the formula: y = f ( x ) is the equation of the curve whose area is being rotated a and b are the limits of the area being rotated dx show that the area is being rotated abount the x-axis.

34. Example 2 Find the volume if the area bounded by the curve y = x 3 + 1, the x- axis and the limits of x = 0 and x = 3 is rotated around the x -axis..

35. When the shaded area is rotated 360° about the x -axis, we again observe that a volume is generated: