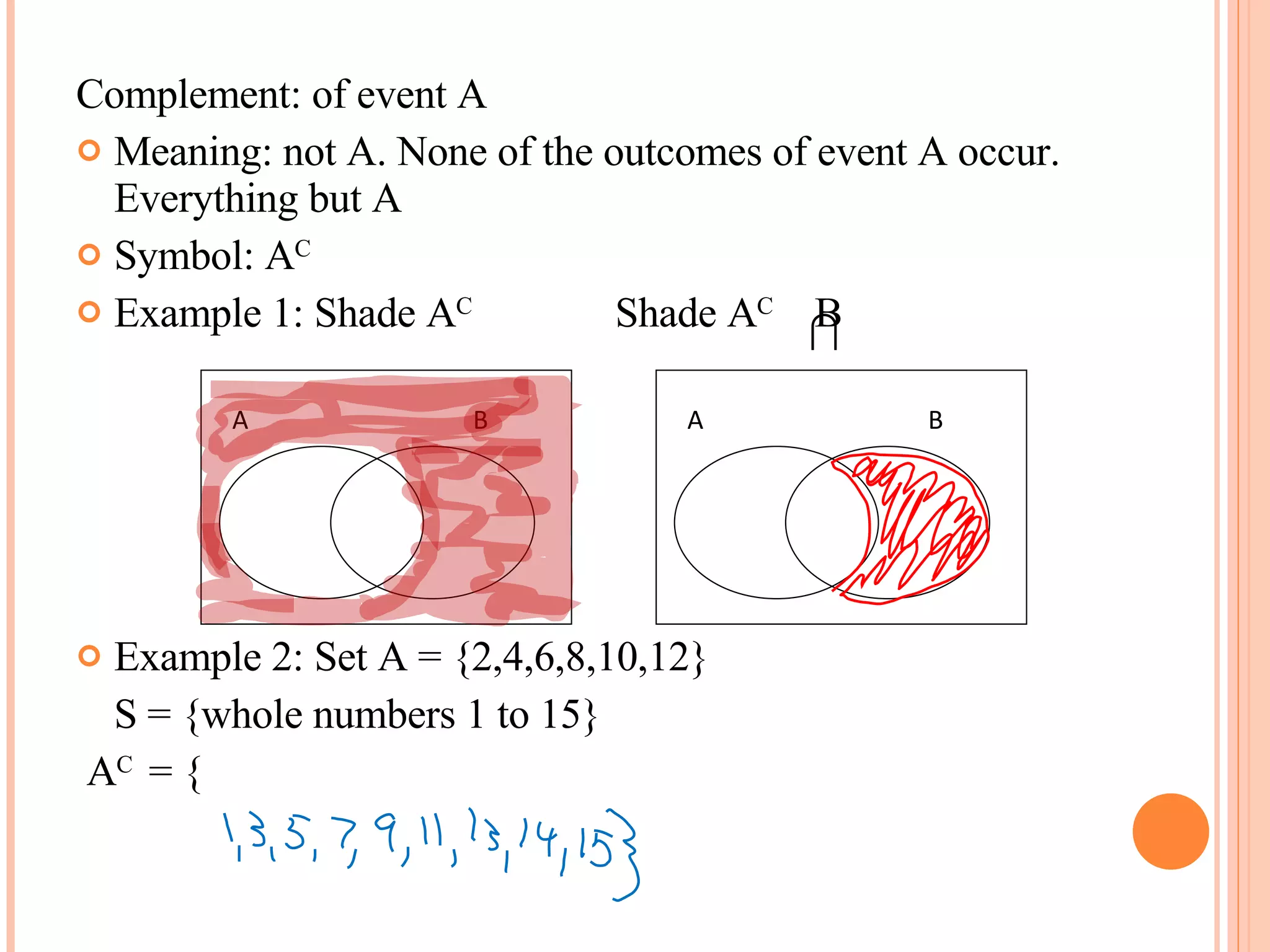
This document introduces key concepts in probability including: - Random events have uncertain outcomes but a regular distribution appears with large numbers of trials. - Probability is the proportion of times an outcome would occur with many trials. - Set theory concepts like unions, intersections, and complements are used to define sample spaces and calculate probabilities. - The three basic probability rules are that probabilities lie between 0 and 1, the probabilities of all outcomes sum to 1, and the probability of an event's complement is 1 minus the probability of the event.

1. CHAPTER 4 - PROBABILITY

2. INTRODUCTORY VOCABULARY Random (trials) – individual outcomes of a trial are uncertain, but when a large number of trials are performed a regular distribution appears Probability – Proportion of times an outcome would occur in a large number of trials Experimental Probability – What did happen in an experiment. The proportion of times an event occurred in an experiment

3. Theoretical Probability – What should happen in an experiment. Usually found by looking at experimental probabilities. Probability Models – List of all possible outcomes The probability of each outcome is then listed. Sample Space – the set of all possible outcomes of an event. S = { } Examples: Rolling a die once; S = {1,2,3,4,5,6} Flipping a coin twice; S = {HH,HT,TH,TT}

4. PROBABILITY NOTATION A,B,C, etc. – events or outcomes P(A) = the probability of outcome A occuring S = sample space When we represent events, we draw them with Venn Diagrams Venn Diagrams use shapes to represent events and a box around the shapes that represents the sample space or all possible outcomes

5. GENERAL SET THEORY Union: “or” statements Meaning: joining, addition Symbol: Example 1: Example 2: Set A = {2,4,6,8,10,12} Set B = {1,2,3,4,5,6,7} A B = A B

6. Intersection: “and” Meaning: overlap, things in common Symbol: Example 1: Example 2: Set A = {2,4,6,8,10,12} Set B = {1,2,3,4,5,6,7} A B = A B

7. Complement: of event A Meaning: not A. None of the outcomes of event A occur. Everything but A Symbol: A C Example 1: Shade A C Shade A C B Example 2: Set A = {2,4,6,8,10,12} S = {whole numbers 1 to 15} A C = { A B A B

8. TRY THE SET THEORY WORKSHEET

9. PROBABILITY RULES! First Three Probability Rules All probabilities lie between 0 and 1 Probability of all possible outcomes must be equal to 1 Probability of the compliment of A is the same as 1 minus the probability of A Example 1:

10. Example 2: Example 3: Type A+ A- B+ B- AB+ AB- O+ O- Prob. 0.16 0.14 0.19 0.17 ? 0.07 0.1 0.11

11. Unions OR => Addition General Rule: Why do we subtract the intersection? We don’t want to count the outcomes in A and B twice, the overlap of A and B. A B

12. Special Case: What if A and B don’t overlap? So This is called Disjoint or Mutually Exclusive No common outcomes

13. Conditional Probability Probability of B happening given that A has already happened. Formula: Example: P(A) = 5/10 P(B) = 3/10 P(B|A) = 3/9 since the first one was not replaced P(B|A)=P(A|B)??

14. Intersections General Rule: Also called the multiplication rule Special Case P(Red) = 3/10 P(Red|Blue) = 3/10 If P(B|A) = P(B) the two events are independent