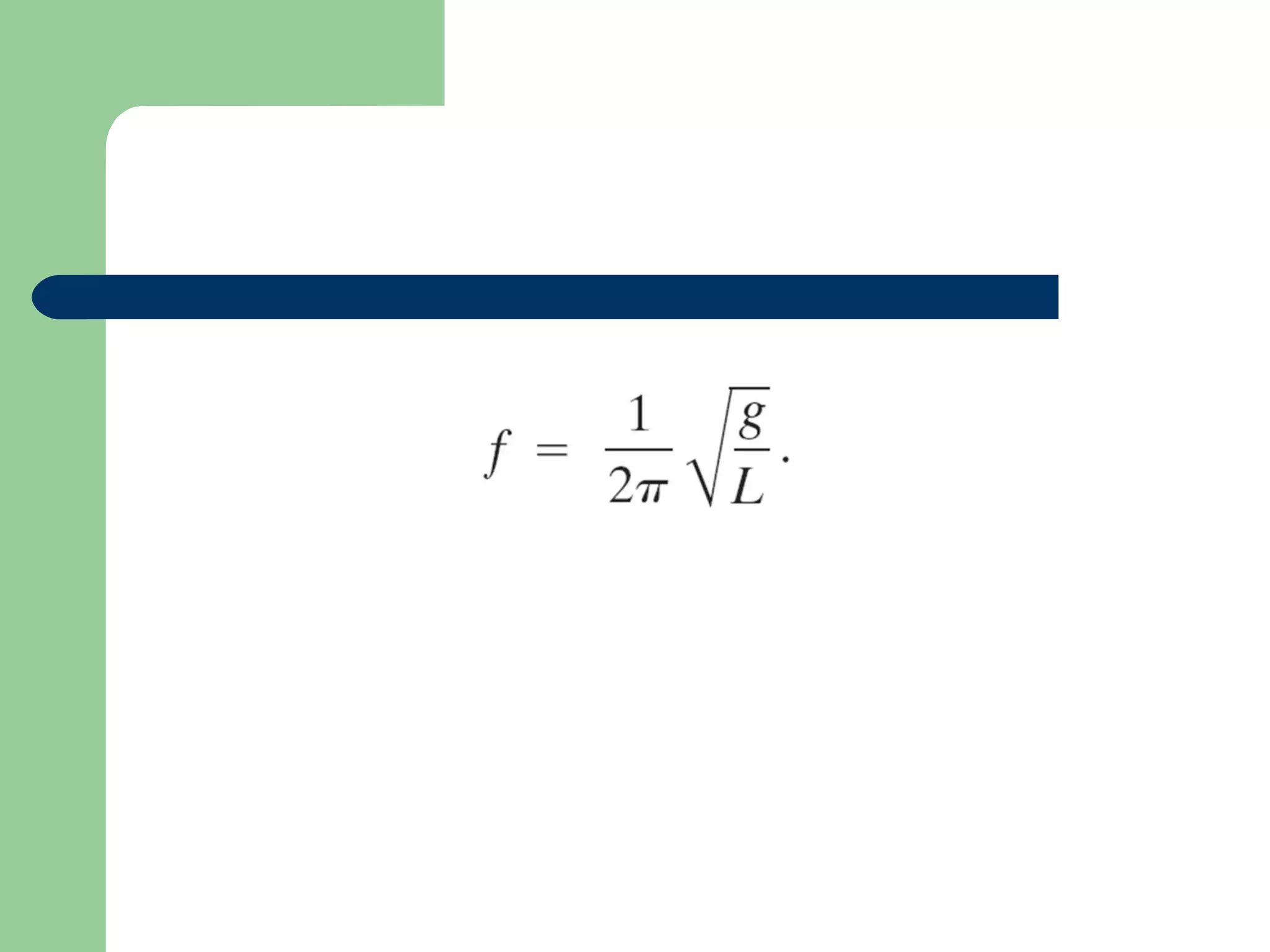This document discusses simple and compound pendulums. A simple pendulum consists of a mass attached to a string that swings back and forth. Its period depends only on its length and gravity. A compound pendulum is a rigid object that pivots, like a door. Its period depends on its length of gyration, moment of inertia, mass, and gravity. For small angles, a compound pendulum behaves similarly to a simple pendulum with an effective length. Both types of pendulums exhibit simple harmonic motion that can be modeled by the same equation.

1. SIMPLE PENDULUM AND
COMPOUND PENDULUM

2. PERIODIC MOTION
 The motion which
repeats itself after
fixed time intervals is
called periodic
motion
The best example of periodic motion are the pendulum clocks.

3. A SIMPLE PENDULUM
 A string with a mass at
the end which is free to
swing is called a
pendulum.

4. TO AND FRO MOTION
 The ball moves to
and fro. It rises to
extreme positions on
both sides and
reverses its motion
 Oscillations gradually
die down

5. LENGTH OF THE PENDULUM
 The length of the
string from the point
of suspension to the
mass is called the
length of the
pendulum.
 It is denoted by L

6. MEAN POSITION OF THE PENDULUM
 The central position of
the pendulum (the
starting position) is
called the mean
position of the
pendulum.
 It is labeled here as B.

7. EXTREME POSITIONS OF THE
PENDULUM
 A and C are the extreme positions of the pendulum.

8. OSCILLATION
 The motion of the mass
from its extreme
position A to C and
back to A is called an
oscillation.

9. TIME TAKEN FOR ONE OSCILLATION
 The time taken for one oscillation is very
short and therefore, difficult to measure
accurately.
 To find the time taken, we find the time taken
for large number say 20 oscillations. This
time divided by 20 will give us time taken for
one oscillation.

10. PERIODIC TIME OF THE SIMPLE
PENDULUM
 The time taken to complete one oscillation is
called the periodic time of the simple
pendulum.
 It is sometimes also called its period and is
denoted by T.

11. RELATIONSHIP BETWEEN LENGTH AND
TIME PERIOD OF THE PENDULUM
 The graph of the
relationship between
length and time period
of the pendulum is a
parabola.
 Thus the relationship
can be expressed as
L=constant X T2

12. VALUE OF CONSTANT
L= constant X T2
constant=
2
T
L
By calculating the value of 2
T
L
2
T
L
for each value of the graph
between L and T2
, the value of the
constant comes out to be 0.248

13. UNITS OF THE CONSTANT
 The constant has the same
units as the acceleration that
is m/s2
 If we try to learn more about
the pendulum, we will find
that the constant is just the
acceleration g due to gravity
divided by
∏
2
4

14. RELATIONSHIP BETWEEN T AND L
 The equation is
∏=
g
L
2T
The Period of the pendulum T is related to the length L
by the relation

15. :
which is proportional to sin θ
and not to θ itself.
However, if the angle is small,
sin θ ≈ θ.
The Simple Pendulum

16. Therefore, for small angles, we have:
Where
,
The period and frequency are:

18. COMPOUND PENDULUM
 The compound pendulum, which is also known as
the physical pendulum, is an extension of the
simple pendulum.
 The physical pendulum is any rigid body that is
pivoted so that it can oscillate freely.
 The compound pendulum has a point called the
center of oscillation.
 This is placed at a distance L from the pivot where
L is given by L = I/mR; here, m is the mass of the
pendulum, I is the moment of inertia over the pivot,
and R is the distance to the center of mass from
the pivot.

19.  The period of oscillation for the physical pendulum
is given by T = L is known as the length of
gyration.

20. Difference between
Simple Pendulum
 The period and,
therefore, the
frequency of the
simple pendulum
depends only on the
length of the string
and the gravitational
acceleration
Compound Pendulum
 The period and the
frequency of the
compound pendulum
depend on the length of
gyration, the moment of
inertia, and the mass of
the pendulum, as well
as the gravitational
acceleration.

21.  Consider an extended body of mass M
with a hole drilled though it.
 Suppose that the body is suspended
from a fixed peg, which passes through
the hole, such that it is free to swing
from

23.  Let P be the pivot point, and let $C$ be the
body's centre of mass, which is located a
distance d from the pivot.
 Let the a be the angle subtended between
the downward vertical (which passes through
point P and the line PC
 The equilibrium state of the compound
pendulum corresponds to the case in which

24. the centre of mass lies vertically below the
pivot point: i.e., the a=0 .
The angular equation of motion of the
pendulum is simply

25. Where,
I is the moment of inertia of the body about the
pivot point, and
T is the torque

26. Using similar arguments to those employed
for the case of the simple pendulum (recalling
that all the weight of the pendulum acts at its
centre of mass),
we can write

27.  Note that the reaction, R , at the peg does not
contribute to the torque, since its line of action
passes through the pivot point.
 Combining the previous two equations, we obtain
the following angular equation of motion of the
pendulum:

28.  It is clear, by analogy with our
previous solutions of such equations,
that the angular frequency of small
amplitude oscillations of a compound
pendulum is given by

29.  Finally, adopting the small angle
approximation , , we arrive at the
simple harmonic equation:

30. It is helpful to define the length:
Equation reduces to :

31. Conclusion
esponding expression for a simple pendulum. We conclude that a compound pendulum behaves like a simple pendulum with effective lengt
 corresponding expression is identical to a
simple pendulum.
 We conclude that a compound pendulum
behaves like a simple pendulum with
effective length L.

32. PRITAM KUMAR(13129)
PRASHANT KUMAR(13126)
PRASHANT SINGH (13127)
PRAVESH PRADHAN(13128)
DONE BY:-
Sem 4
Div 4