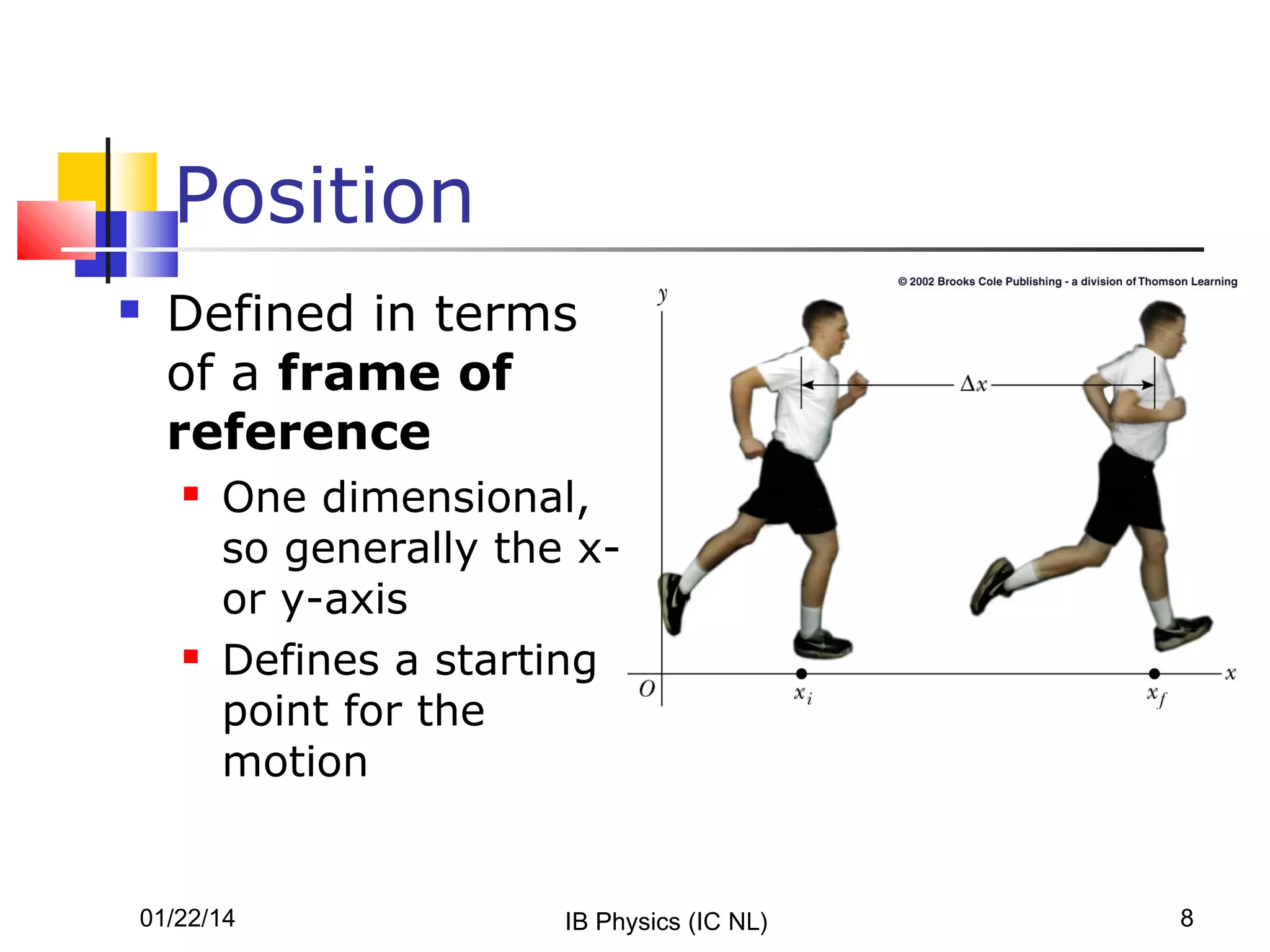
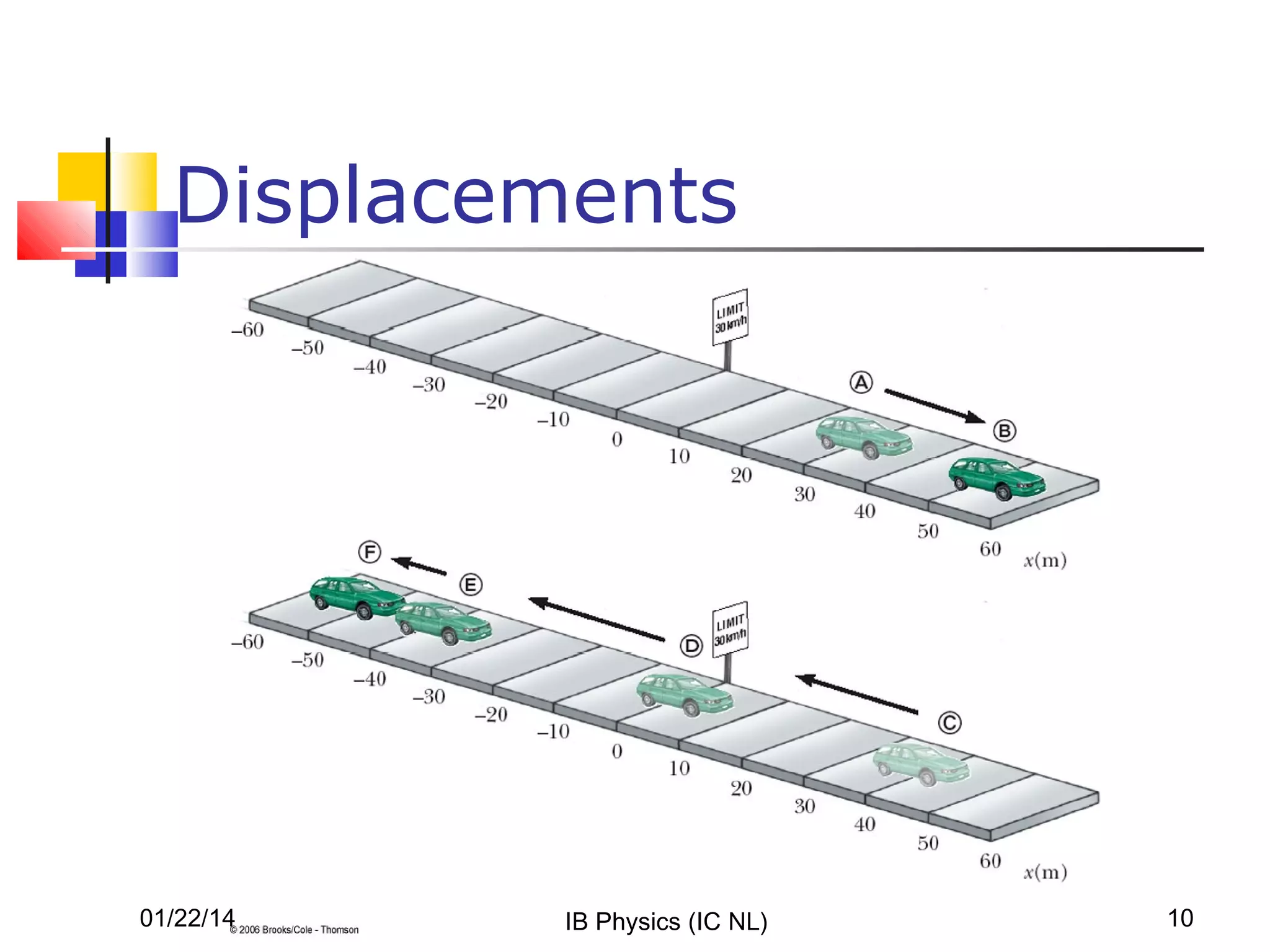
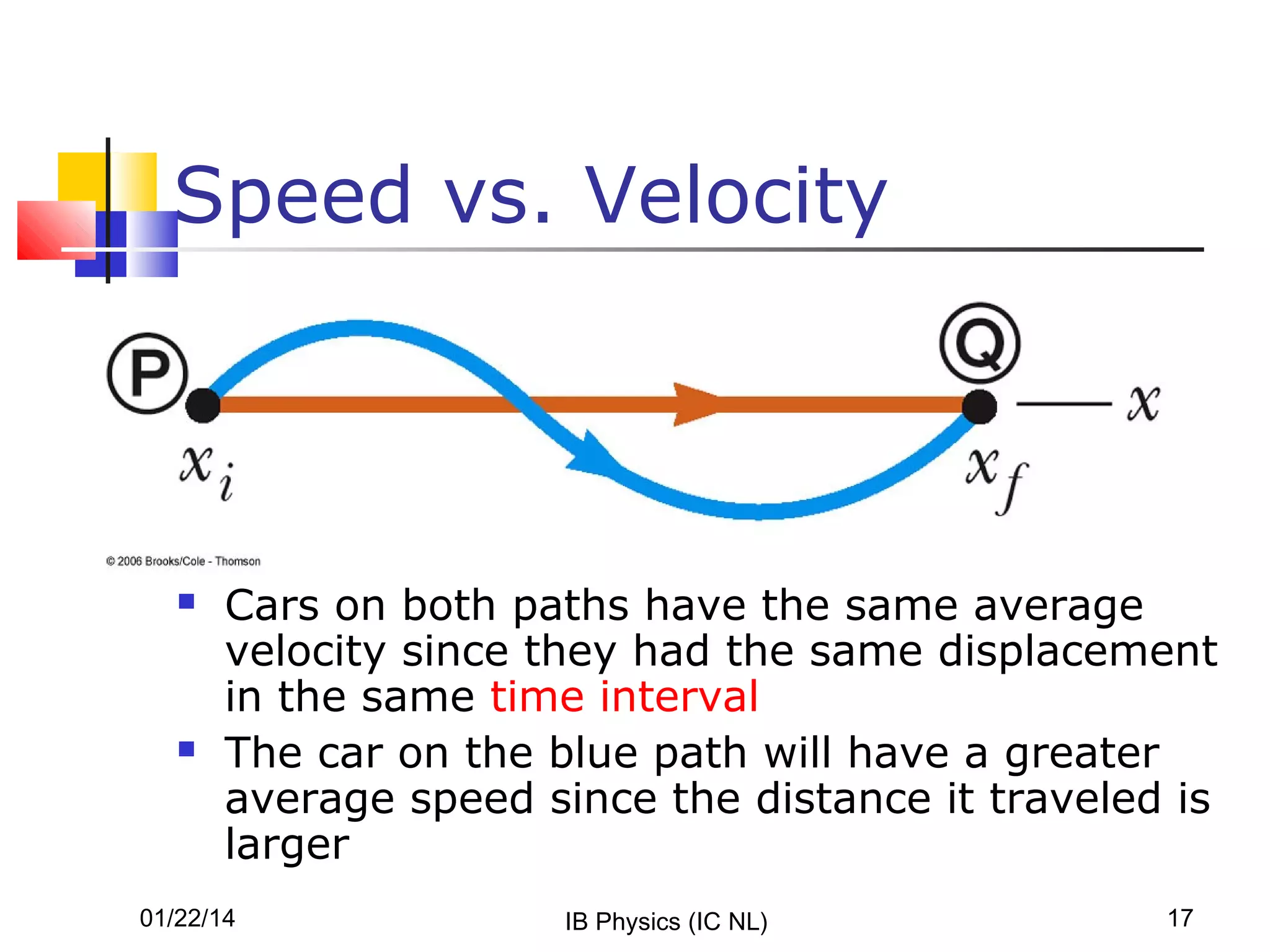
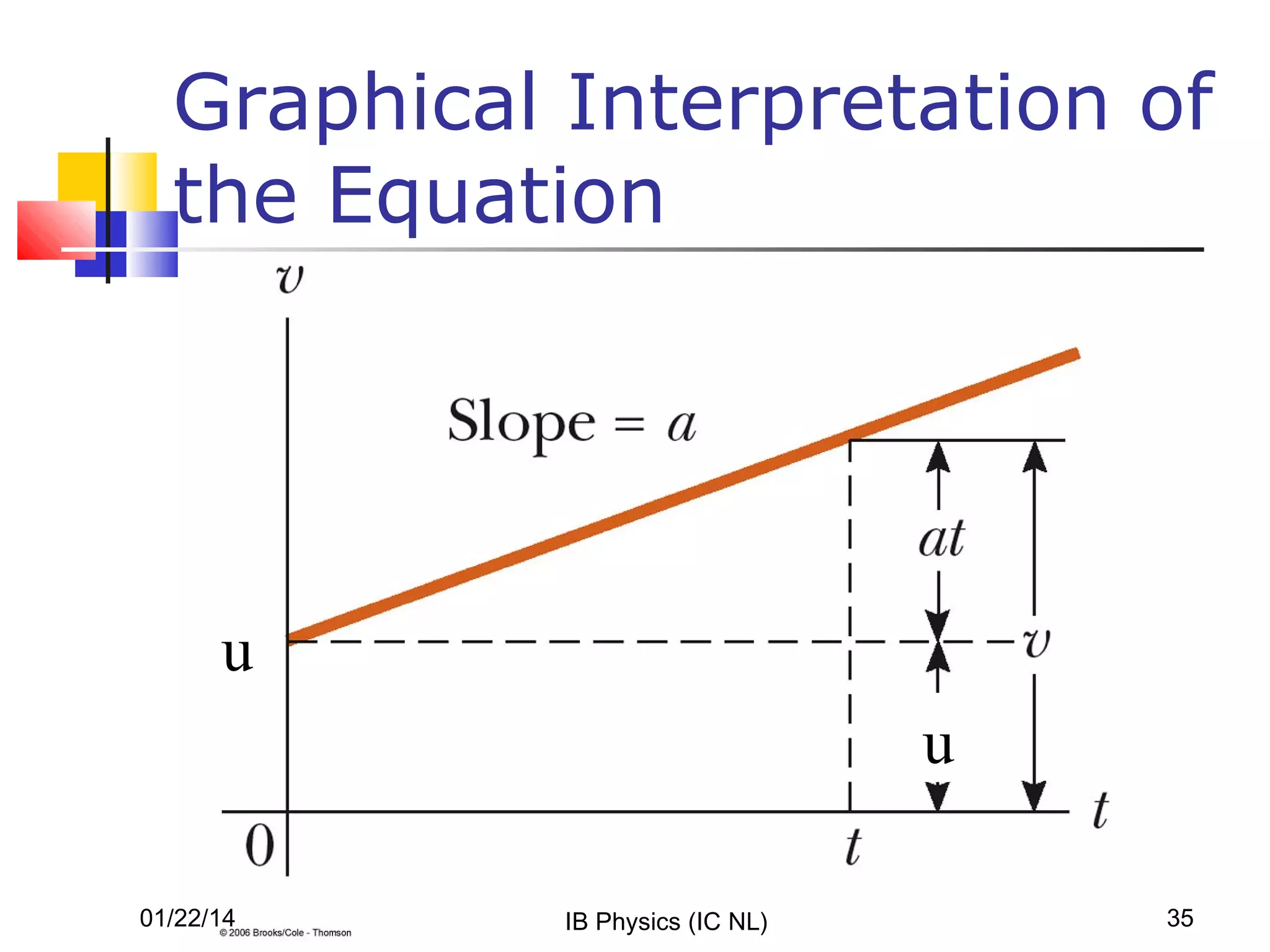
This document provides an overview of motion in one dimension, including: - Kinematics is the study of motion without considering causes of motion or forces. It examines displacement, velocity, and acceleration. - Displacement is the change in position of an object. Velocity is the rate of change of displacement, or how displacement changes over time. It has both magnitude and direction. - For constant velocity, the kinematic equations are simple. But when acceleration is involved, more complex equations relate variables like displacement, time, initial/final velocities, and acceleration. 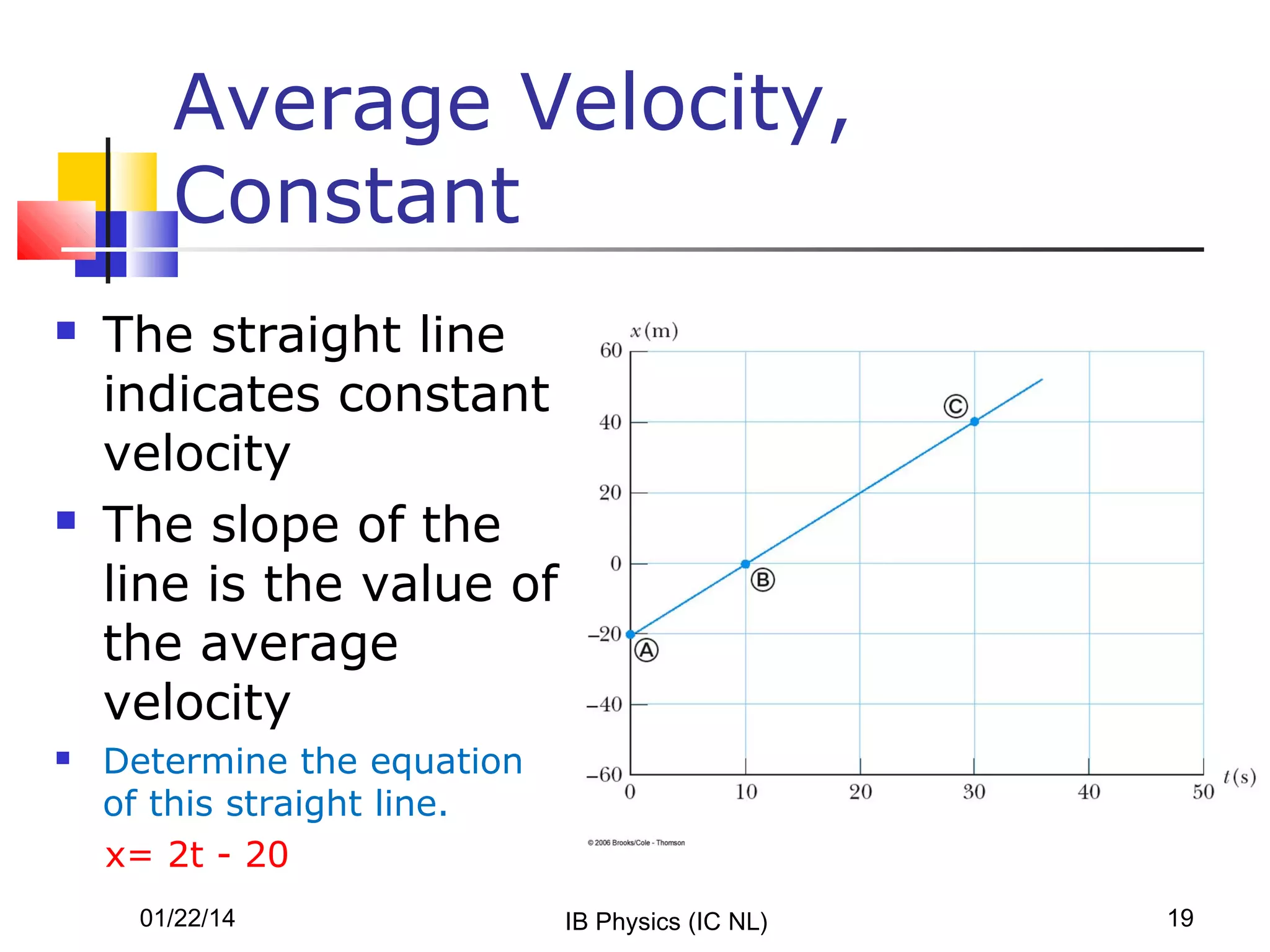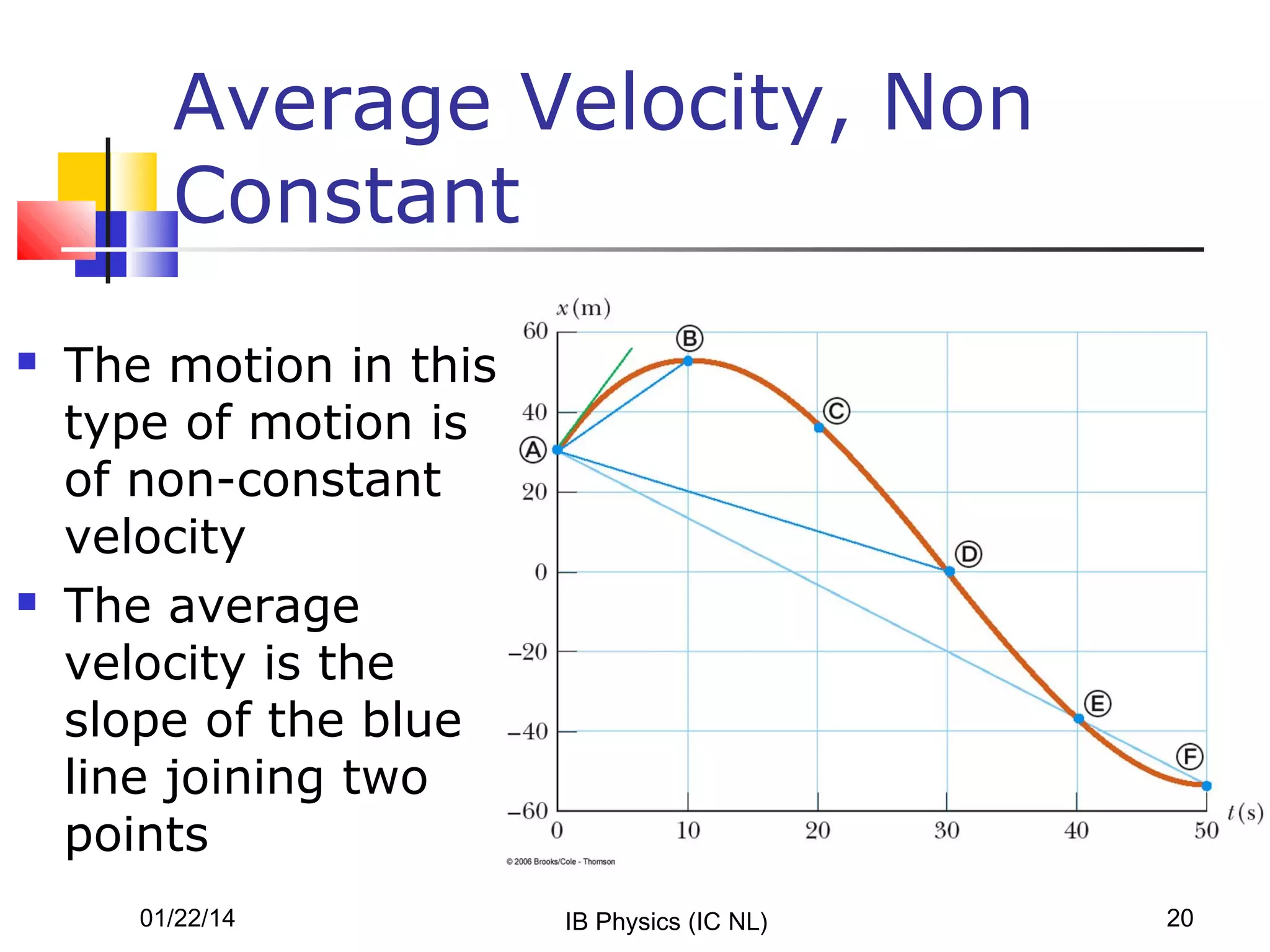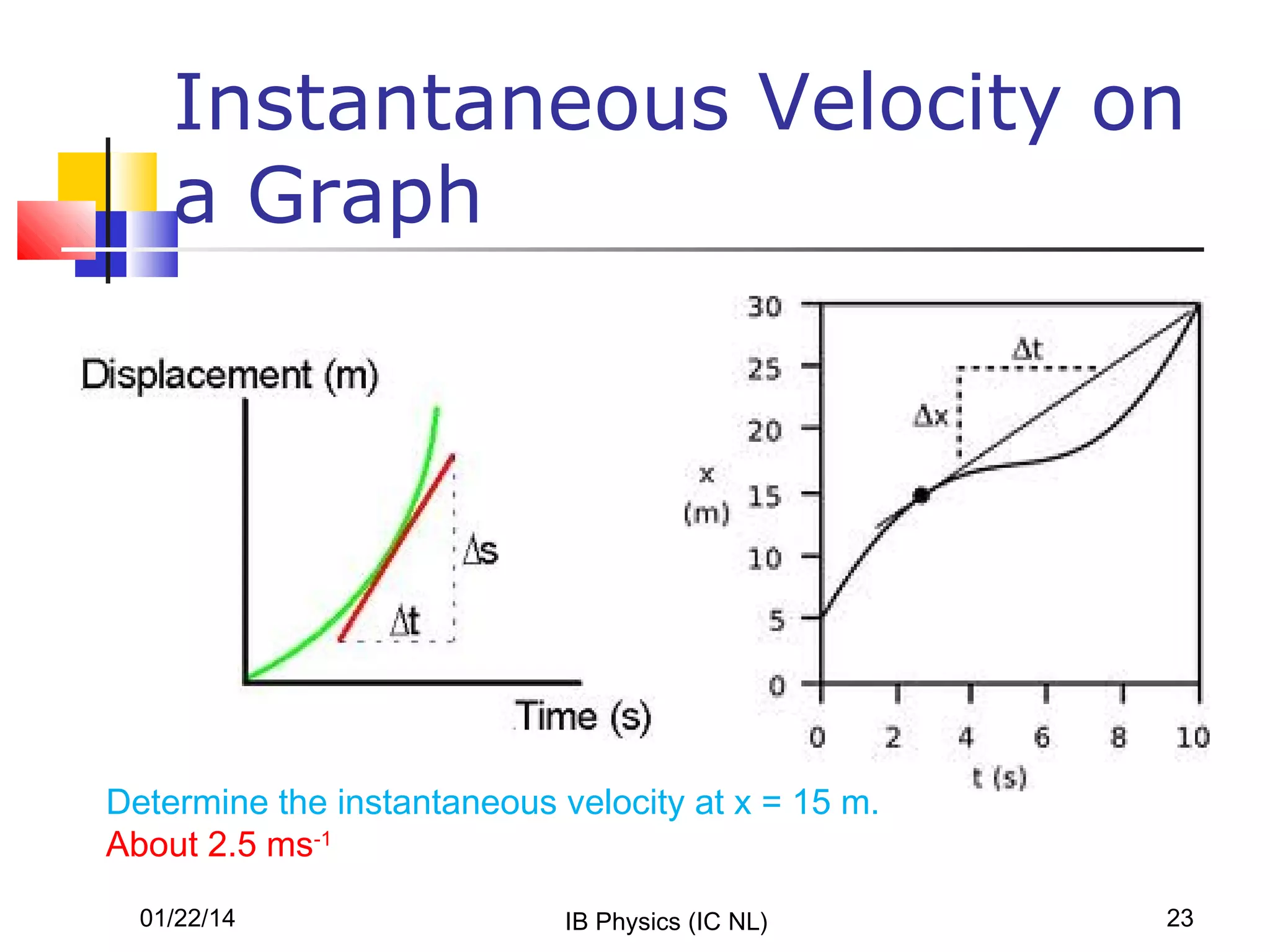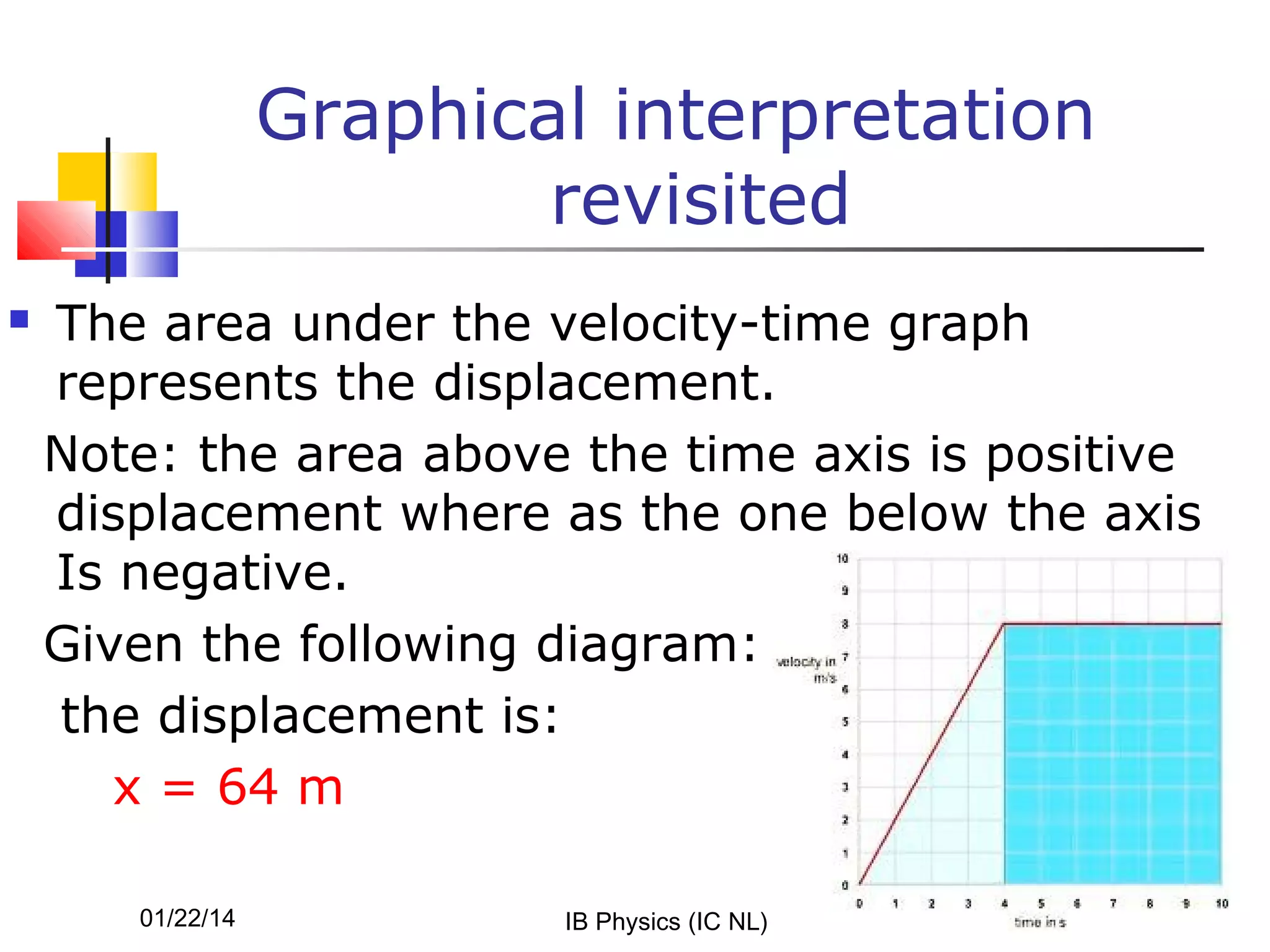- Graphs of position versus time can reveal if velocity or acceleration are constant or changing. The slope and shape of the graph provide kinetic information.

1. Chapter 2
Motion in One Dimension
01/22/14
IB Physics (IC NL)
1

2. Mechanics
Mechanics is a branch of physics
concerned with the behavior of physical
bodies when subjected to forces or
displacements also it deals with matter
and investigates energy.
Mechanics is divided into three branches:
1- Statics
2- Kinematics
3- Dynamics
In this slide we will discuss
01/22/14
KINEMATICS.
IB Physics (IC NL)
2

3. Kinematics

Kinematics is a part of mechanics that
studies motion in relationship to time.


In kinematics, you are interested in the
description of motion
Not concerned with the cause of the motion
(Dynamics) or bodies at rest (statics)
01/22/14
IB Physics (IC NL)
3

4. Motion



A body or object is said to be in motion when it is
observed moving or changing position relative to
a fixed reference as time passes.
Therefore motion is relative; example when you
are in a car and you take the moving car as your
reference then you see a building moving back
relative to you.
Then there should exist a reference frame to your
work and since we are studying this topic while
on Earth, we suppose the Earth is our reference
frame thus it is called the terrestrial frame.
01/22/14
IB Physics (IC NL)
4

5. Motion cont.


Motion, to our level, is studied either according
to trajectory or according to speed.
The trajectory is the path followed by the
center of mass of a moving object.
Remark: our object could be:
1- either a solid body of considerable dimensions with a
center of mass where all the mass of the object is
concentrated (also called center of gravity)
2- or a point mass with relative negligible dimensions and
the mass is concentrated at the point itself.
Hint: don’t worry about this the question usually identifies
the type of the object.

01/22/14
IB Physics (IC NL)
5

6. Motion according to trajectory.
Studying the motion according to
trajectory is very wide so we are
limiting it to a general one which is
curvilinear and includes one of three:
 Rectilinear: along a straight line
 Circular: along a circle
 Curvilinear along a curve.
The first study is the rectilinear motion
that is motion in one dimension.

01/22/14
IB Physics (IC NL)
6

7. Quantities in Motion

Any motion involves three
concepts




Displacement
Velocity
Acceleration
These concepts can be used to
study objects in motion
01/22/14
IB Physics (IC NL)
7

8. Position

Defined in terms
of a frame of
reference


One dimensional,
so generally the xor y-axis
Defines a starting
point for the
motion
01/22/14
IB Physics (IC NL)
8

9. Displacement

Defined as the change in position
or how much the object was
displaced from its initial position.

∆x ≡ xf − xi



01/22/14
f stands for final and i stands for initial
May be represented as ∆y if vertical
Units are meters (m) in SI,
centimeters (cm) in cgs.
IB Physics (IC NL)
9

10. Displacements
01/22/14
IB Physics (IC NL)
10

11. Vector and Scalar
Quantities

Vector quantities need both
magnitude (size) and direction to
completely describe them



Generally denoted by boldfaced type
and an arrow over the letter
+ or – sign is also used in vector
representation.
Scalar quantities are completely
described by magnitude only
01/22/14
IB Physics (IC NL)
11

12. Displacement Isn’t
Distance

The displacement of an object is
not the same as the distance it
travels

Example: Throw a ball straight up
and then catch it at the same point
you released it


01/22/14
The distance is twice the height
The displacement is zero
IB Physics (IC NL)
12

13. Speed

The average speed of an object is
defined as the total distance traveled
divided by the total time elapsed
total distance
Average speed =
total time
d
v =
t

01/22/14
Speed is a scalar quantity
IB Physics (IC NL)
13

14. Speed, cont



Average speed totally ignores any
variations in the object’s actual
motion during the trip
The total distance and the total
time are all that is important
SI unit m.s-1
01/22/14
IB Physics (IC NL)
14

15. Velocity



It takes time for an object to
undergo a displacement
The average velocity is rate at
which the displacement occurs or
simply the rate of change of
displacement.
∆ x xf − xi
v average =
=
∆t
tf − ti
generally use a time interval, so let ti = 0
01/22/14
IB Physics (IC NL)
15

16. Velocity continued

Direction will be the same as the
direction of the displacement (time
interval is always positive)


+ or - is sufficient
Units of velocity is also m.s-1 (SI)

01/22/14
Other units may be given in a
problem, but generally will need to be
converted to m.s-1 these like km/h
IB Physics (IC NL)
16

17. Speed vs. Velocity


Cars on both paths have the same average
velocity since they had the same displacement
in the same time interval
The car on the blue path will have a greater
average speed since the distance it traveled is
larger
01/22/14
IB Physics (IC NL)
17

18. Graphical Interpretation of
Velocity



Velocity can be determined from a
position-time graph
Average velocity equals the slope
of the line joining the initial and
final positions
An object moving with a constant
velocity will have a graph that is a
straight line.
01/22/14
IB Physics (IC NL)
18

19. Average Velocity,
Constant



The straight line
indicates constant
velocity
The slope of the
line is the value of
the average
velocity
Determine the equation
of this straight line.
x= 2t - 20
01/22/14
IB Physics (IC NL)
19

20. Average Velocity, Non
Constant


The motion in this
type of motion is
of non-constant
velocity
The average
velocity is the
slope of the blue
line joining two
points
01/22/14
IB Physics (IC NL)
20

21. Instantaneous Velocity



The limit of the average velocity as the
time interval becomes infinitesimally
short, or as the time interval approaches
zero
lim ∆x
v ≡ ∆t → 0
∆t
The instantaneous velocity indicates what
is happening at every instant of time. It
is a function of time.
The speedometer of a car indicates the
instantaneous speed.
01/22/14
IB Physics (IC NL)
21

22. Instantaneous Velocity on
a Graph

The slope of the line tangent to the
position-vs.-time graph is defined
to be the instantaneous velocity at
that time

01/22/14
The instantaneous speed is defined as
the magnitude of the instantaneous
velocity
IB Physics (IC NL)
22

23. Instantaneous Velocity on
a Graph
Determine the instantaneous velocity at x = 15 m.
About 2.5 ms-1
01/22/14
IB Physics (IC NL)
23

24. Motion according to speed
In this part we study the motion of an
object depending on its velocity along a
rectilinear trajectory.
 Our study is limited now to:
1- motion with constant speed or velocity
and called uniform motion (URM)
2- motion with a constantly varying
velocity and called uniformly
accelerated motion. (UARM)

01/22/14
IB Physics (IC NL)
24

25. Uniform rectilinear motion


URM is motion with constant
velocity
The instantaneous velocities are
always the same

01/22/14
All the instantaneous velocities will
also equal the average velocity
IB Physics (IC NL)
25

26. Kinematic equations of
URM









a=0
v = constant
x = vt + xo
Where:
a is acceleration
v is velocity
x is displacement
xo is initial displacement or distance
covered when started timing
and t is time
01/22/14
IB Physics (IC NL)
26

27. Acceleration



Changing velocity (not-uniform)
means an acceleration is present
Acceleration is the rate of change
of the velocity
∆v vf − vi
a=
=
∆t
tf − ti
Units is ms-² (SI)
01/22/14
IB Physics (IC NL)
27

28. Relationship Between
Acceleration and Velocity


Uniform velocity (shown by red arrows
maintaining the same size)
Acceleration equals zero
01/22/14
IB Physics (IC NL)
28

29. Relationship Between
Velocity and Acceleration
Velocity and acceleration are in the same
direction
 Acceleration is uniform (blue arrows maintain
the same length)
 Velocity is increasing uniformly (red arrows are
getting longer)
 Positive velocity and positive acceleration, thus
Accelerated motion. va>0
01/22/14
29
IB Physics (IC NL)


30. Relationship Between
Velocity and Acceleration




Acceleration and velocity are in opposite
directions
Acceleration is uniform (blue arrows maintain
the same length)
Velocity is decreasing uniformly (red arrows
are getting shorter)
Velocity is positive and acceleration is
negative, thus decelerated motion. va<0
01/22/14
IB Physics (IC NL)
30

31. Kinematic Equations

Used in situations with uniform
acceleration
a = const.
1
v = u + at
2
1
3
∆x = vt = ( u + v ) t
2
1 2
4
∆x = ut + at
2
v 2 = u2 + 2a∆x
5
01/22/14
IB Physics (IC NL)
31

32. Kinematic equations cont.
Equation 4 is derive when
plugging equation 2 in
equation 3
 Equation 5 is obtained when
eliminating t from equation 2
and plug it in equation 3

01/22/14
IB Physics (IC NL)
32

33. Notes on the equations
v i +v f 
∆ x = v average t = 
t
 2 


Gives displacement as a function
of velocity and time.
Use when you don’t know and
aren’t asked for the acceleration.
01/22/14
IB Physics (IC NL)
33

34. Notes on the equations
v = u + at


Shows velocity as a function of
acceleration and time
Use when you don’t know and aren’t
asked to find the displacement
01/22/14
IB Physics (IC NL)
34

35. Graphical Interpretation of
the Equation
u
u
01/22/14
IB Physics (IC NL)
35

36. Notes on the equations
1 2
∆ x = ut + at
2


Gives displacement as a function
of time, velocity and acceleration
Use when you don’t know and
aren’t asked to find the final
velocity
01/22/14
IB Physics (IC NL)
36

37. Displacement-time graph
01/22/14
IB Physics (IC NL)
37

38. Acceleration graph

When you are given a displacementtime graph and the figure simulates a
smiling face then the motion is
accelerated. If it is a gloomy face then
the motion is decelerated.
01/22/14
IB Physics (IC NL)
38

39. Notes on the equations
2
2
v = u + 2a∆ x


Gives velocity as a function of
acceleration and displacement
Use when you don’t know and
aren’t asked for the time
01/22/14
IB Physics (IC NL)
39

40. Graphical interpretation
revisited

The area under the velocity-time graph
represents the displacement.
Note: the area above the time axis is positive
displacement where as the one below the axis
Is negative.
Given the following diagram:
the displacement is:
x = 64 m
01/22/14
IB Physics (IC NL)
40

41. Graphical interpretation
revisited
The area under the accelerationtime graph represents the change
in velocity.
 Given the following graph:
 What is the velocity
relative to this motion:
v = 45 ms-1

01/22/14
IB Physics (IC NL)
41

42. Problem-Solving Hints


Read the problem
Draw a diagram


Label all quantities, be sure all the units are
consistent



Choose a coordinate system, label initial and final
points, indicate a positive direction for velocities
and accelerations
Convert if necessary
Specify the type of motion according to a.
Choose the appropriate kinematic equation
01/22/14
IB Physics (IC NL)
42

43. Problem-Solving Hints,
cont

Solve for the unknowns


You may have to solve two equations
for two unknowns
Check your results


01/22/14
Estimate and compare
Check units
IB Physics (IC NL)
43

44. Galileo Galilei



1564 - 1642
Galileo formulated
the laws that govern
the motion of objects
in free fall
Also looked at:




01/22/14
Inclined planes
Relative motion
Thermometers
Pendulum
IB Physics (IC NL)
44

45. Free Fall

All objects moving under the influence
of gravity only are said to be in free fall



Free fall does not depend on the object’s
original motion
All objects falling near the earth’s
surface fall with a constant acceleration
The acceleration is called the
acceleration due to gravity, and
indicated by g
01/22/14
IB Physics (IC NL)
45

46. Laws of free fall



First law: in vacuum and in the same
place, all bodies, dense or light obey the
same law of fall.
Second law: the trajectory followed by a
freely falling object is the vertical,
directed towards the center of the earth.
Third law: the motion of a freely falling
object is uniformly accelerated of
acceleration g.
01/22/14
46
IB Physics (IC NL)

47. Free fall on the moon
01/22/14
IB Physics (IC NL)
47

48. Hyperlink for previous page

Apollo 15 Hammer/Feather gravity
demonstration
01/22/14
IB Physics (IC NL)
48

49. Motion in air



Consequence: In air and in the same
place, dense bodies only and at the
beginning of their fall obey the same law
of fall as in vacuum.
When an object falls in air it is subjected
to friction with air particles and to an
opposing force called air resistance R.
R=kSV2
01/22/14
(go Physics the following slide)
49
IB to (IC NL)

50. Air resistance cont.
R = kSV2
R is air resistance
k is the aerodynamic constant depending
on the shape of the object.
S is cross-sectional area of object.
V is velocity of object.
01/22/14
IB Physics (IC NL)
50

51. Aerodynamic shape and k.
For each shape there is a different k.
The last shape F has the least k so that air resistance is
minimal thus this shape is recommended for the use in
airplanes and it is called the aerodynamic shape.
Note: the object is moving to the left.
01/22/14
IB Physics (IC NL)
51

52. Terminal velocity


When the air resistance reaches a
value that balances the weight of the
object then
Ksv2=mg
mg
v=
ks

This velocity is called the terminal
velocity with which the object
continues falling and it is constant.
01/22/14
IB Physics (IC NL)
52

53. Acceleration due to
Gravity


Symbolized by g
g = 9.80 ms-²


g is always directed downward


When estimating, use g ≈ 10 m.s-2
toward the center of the earth
Ignoring air resistance and assuming g
doesn’t vary with altitude over short
vertical distances, free fall is constantly
accelerated motion
01/22/14
IB Physics (IC NL)
53

54. Free Fall – an object
dropped



Initial velocity is
zero
Let up be positive
Use the kinematic
equations


u= 0
a=g
Generally use y
instead of x since
vertical
Acceleration is g
= -9.80 m.s-2
01/22/14
IB Physics (IC NL)
54

55. Free Fall – an object
thrown downward


a = g = -9.80
m.s-2
Initial velocity ≠ 0

01/22/14
With upward
being positive,
initial velocity will
be negative
IB Physics (IC NL)
55

56. Free Fall -- object thrown
upward



Initial velocity is
upward, so positive
The instantaneous
velocity at the
maximum height is
zero
a = g = -9.80 m.s-2
everywhere in the
motion
01/22/14
IB Physics (IC NL)
u=0
56

57. Thrown upward, cont.

The motion may be symmetrical



Then tup = tdown
Then v = -u
The motion may not be symmetrical

You can break the motion into various
parts to understand but it is
recommendable that you don’t do this and
stick to one system of axes with specified
directions that don’t change with the
motion of the object.
Generally in initial direction of motion of the
01/22/14
IB Physics (IC NL)
object.

57

58. Non-symmetrical
Free Fall


No need to divide the
motion into segments
Object thrown up:
Vertical axis directed
upwards
 Horizontal axis through
projection point O.
 Above O, displacement is
positive
 Below O, displacement is
negative.
01/22/14
IB Physics (IC NL)

58

59. Combination Motions
01/22/14
IB Physics (IC NL)
59