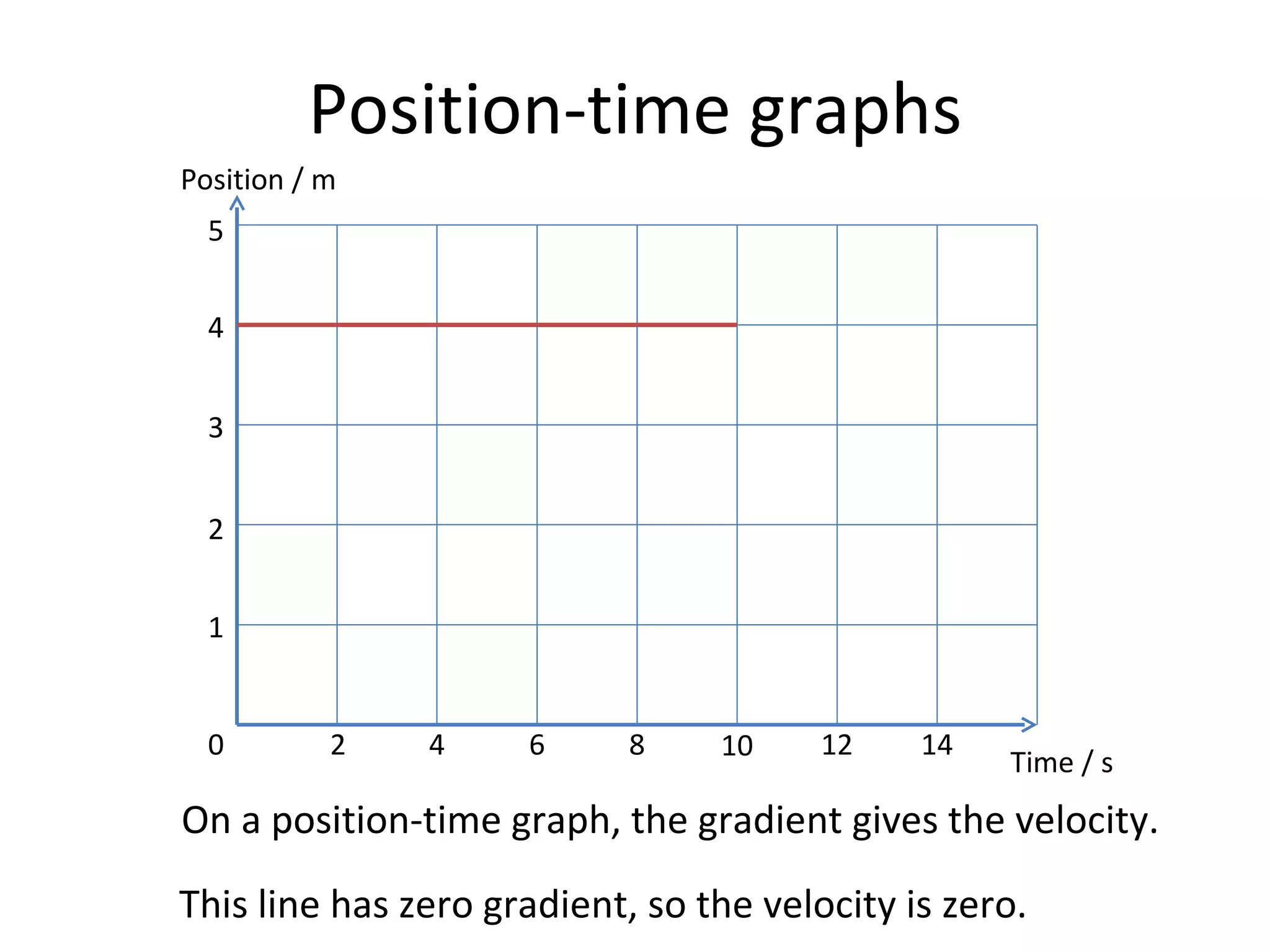
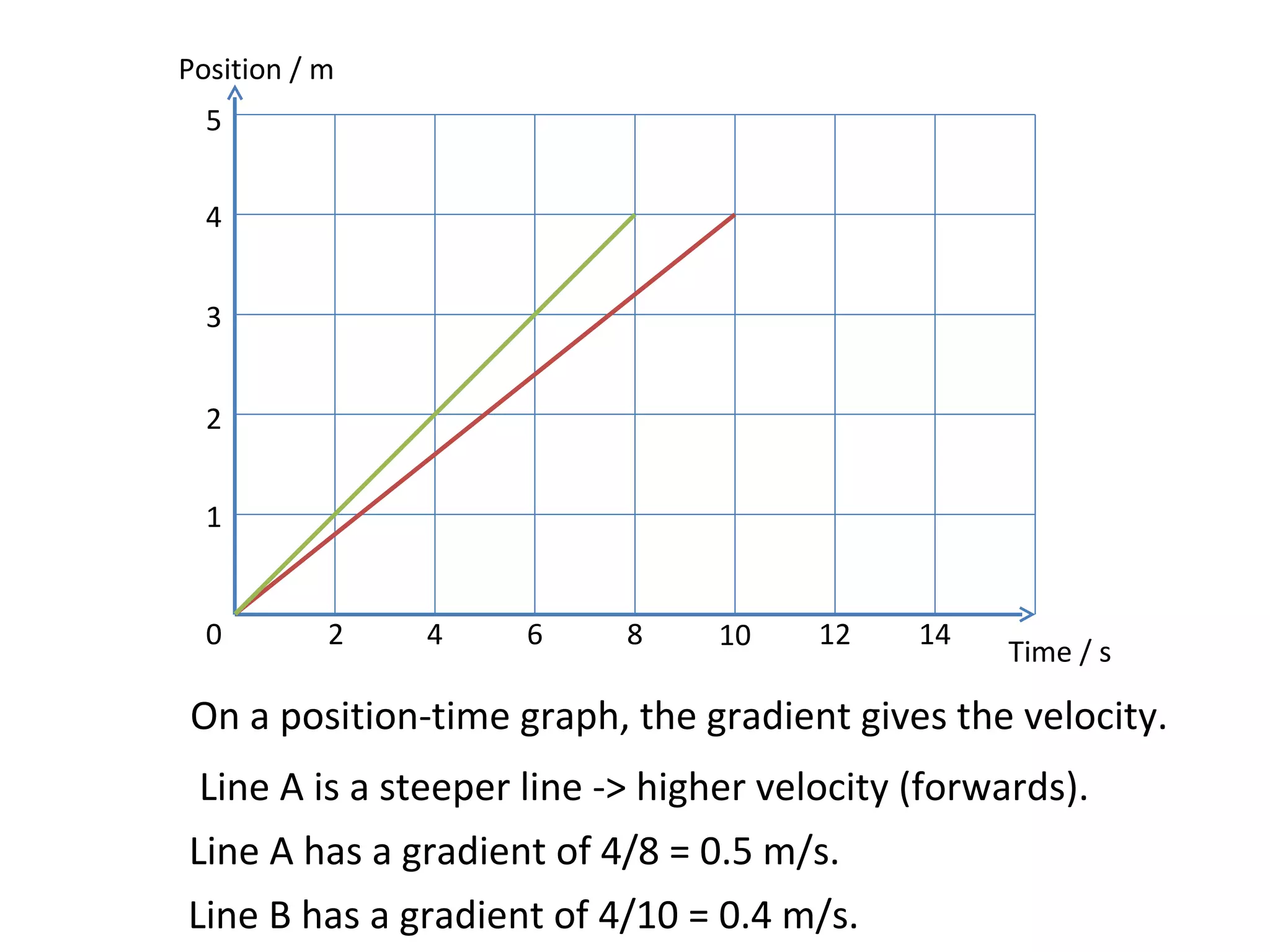
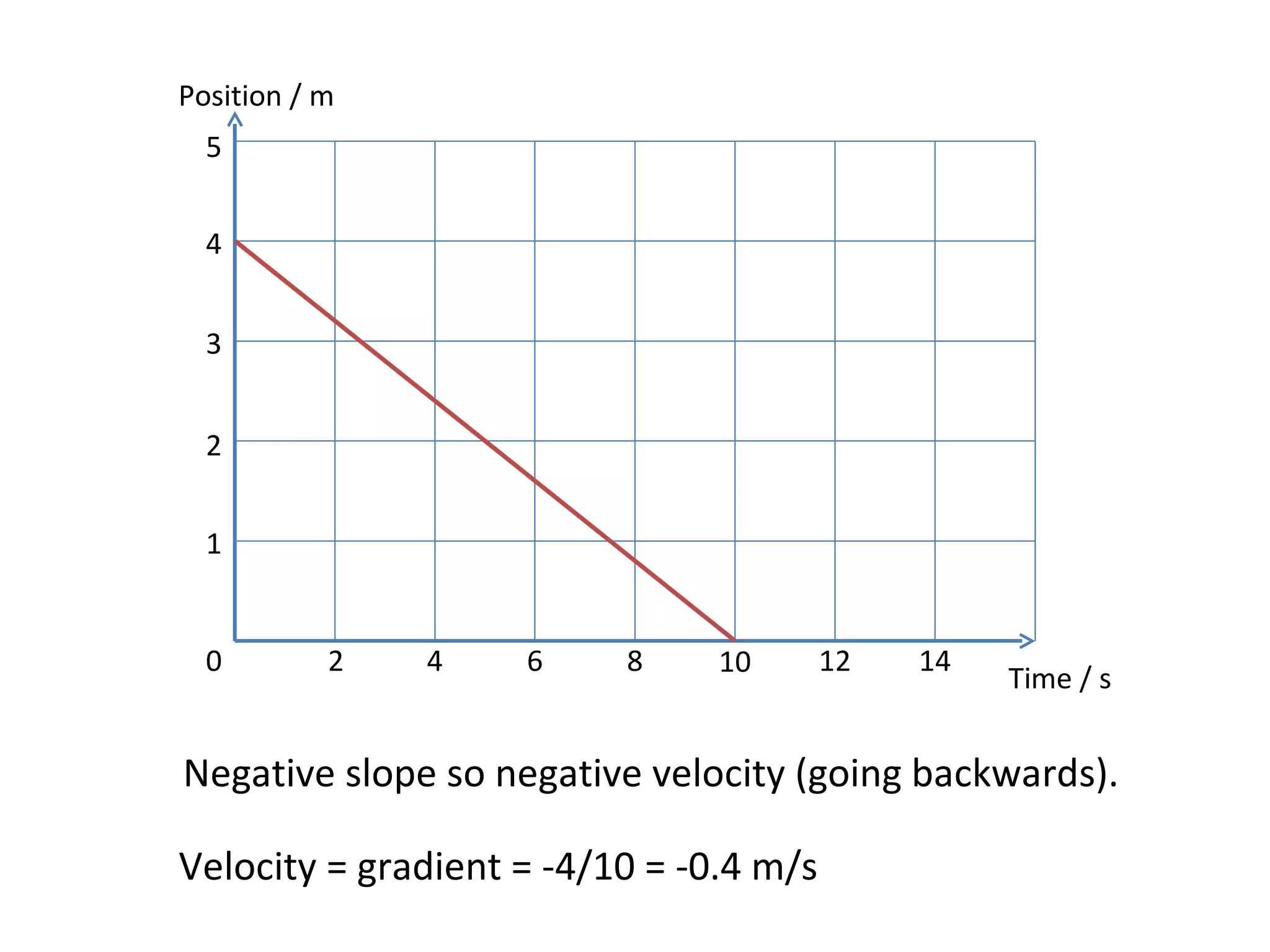
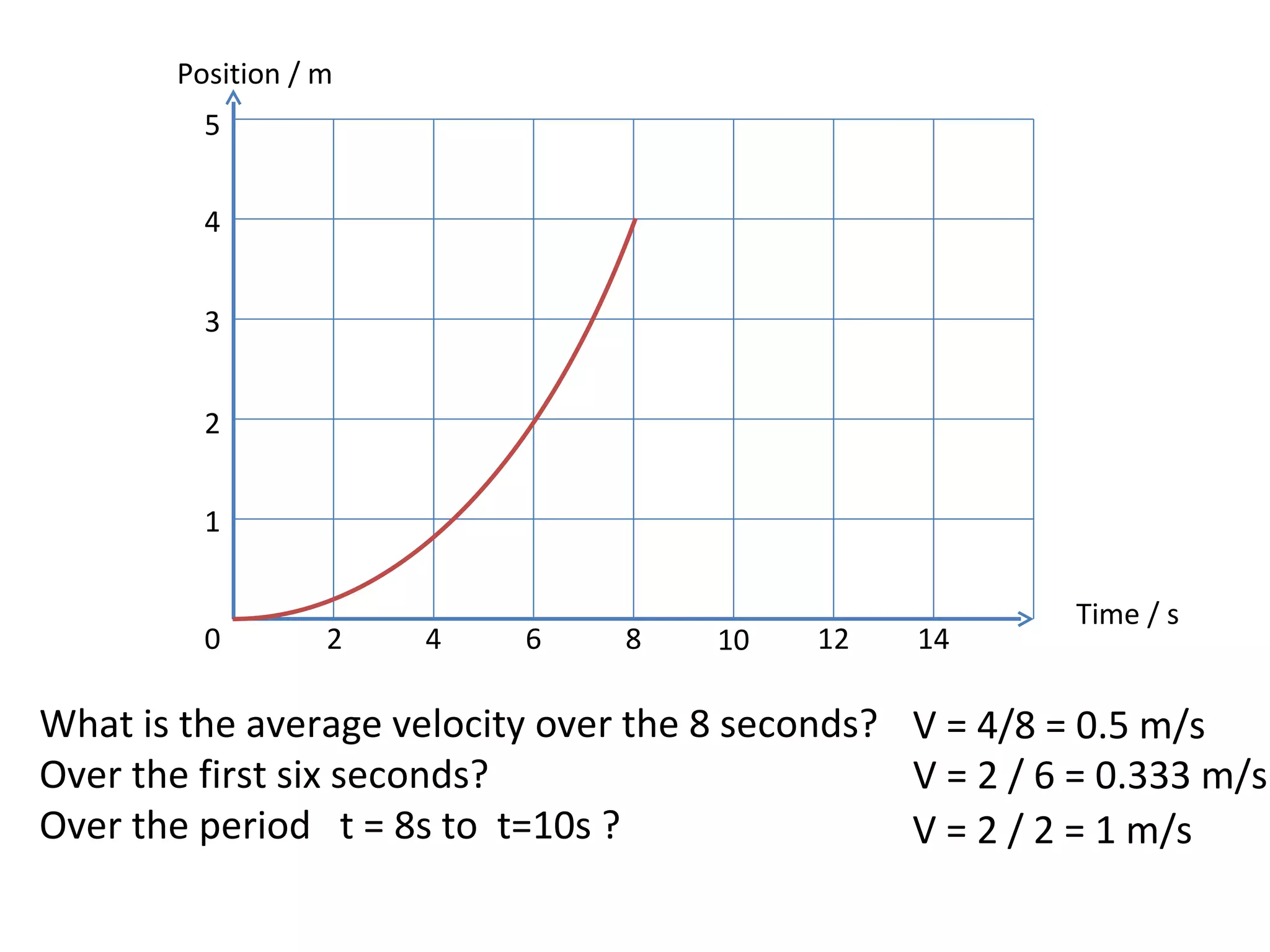
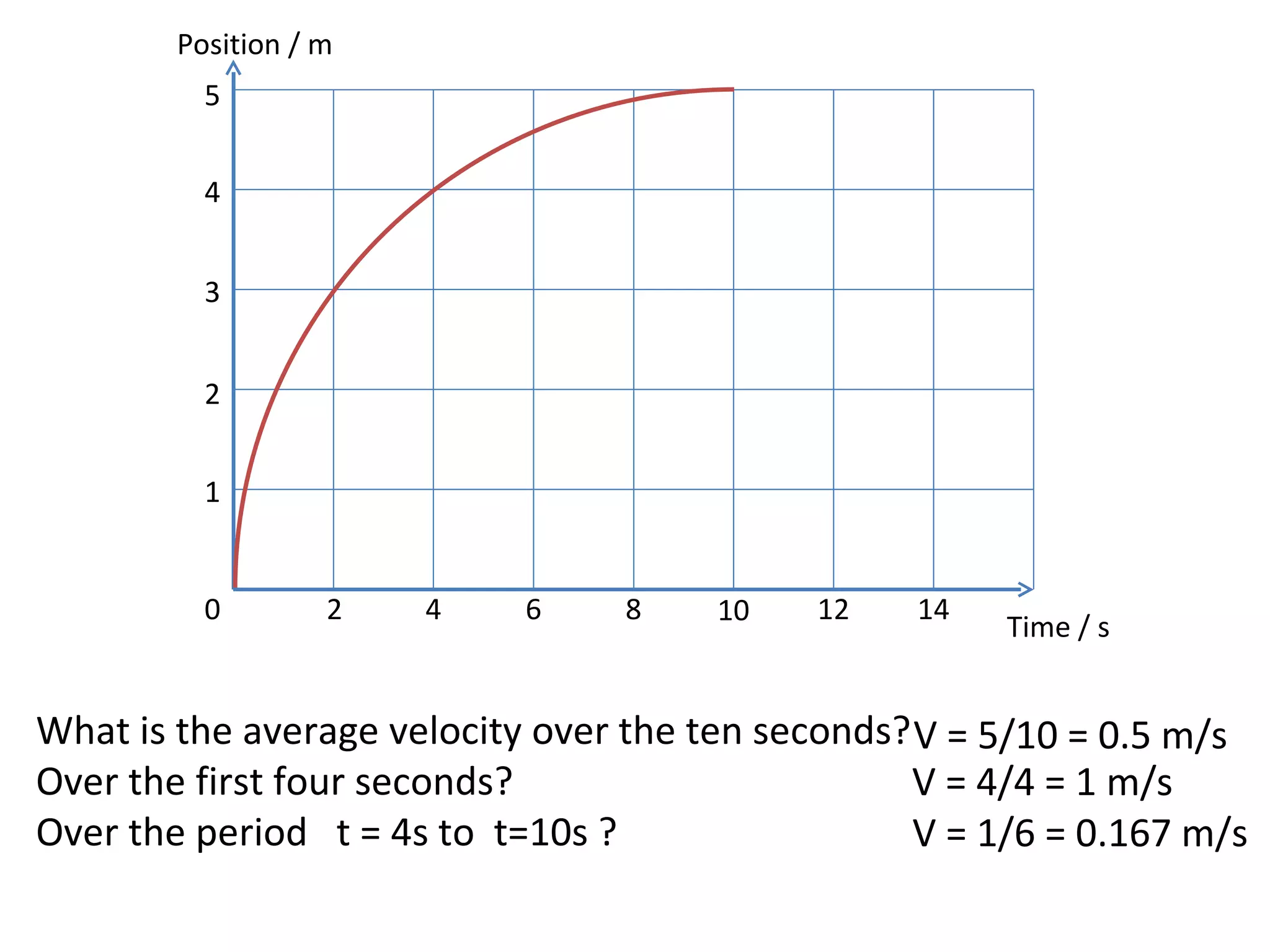
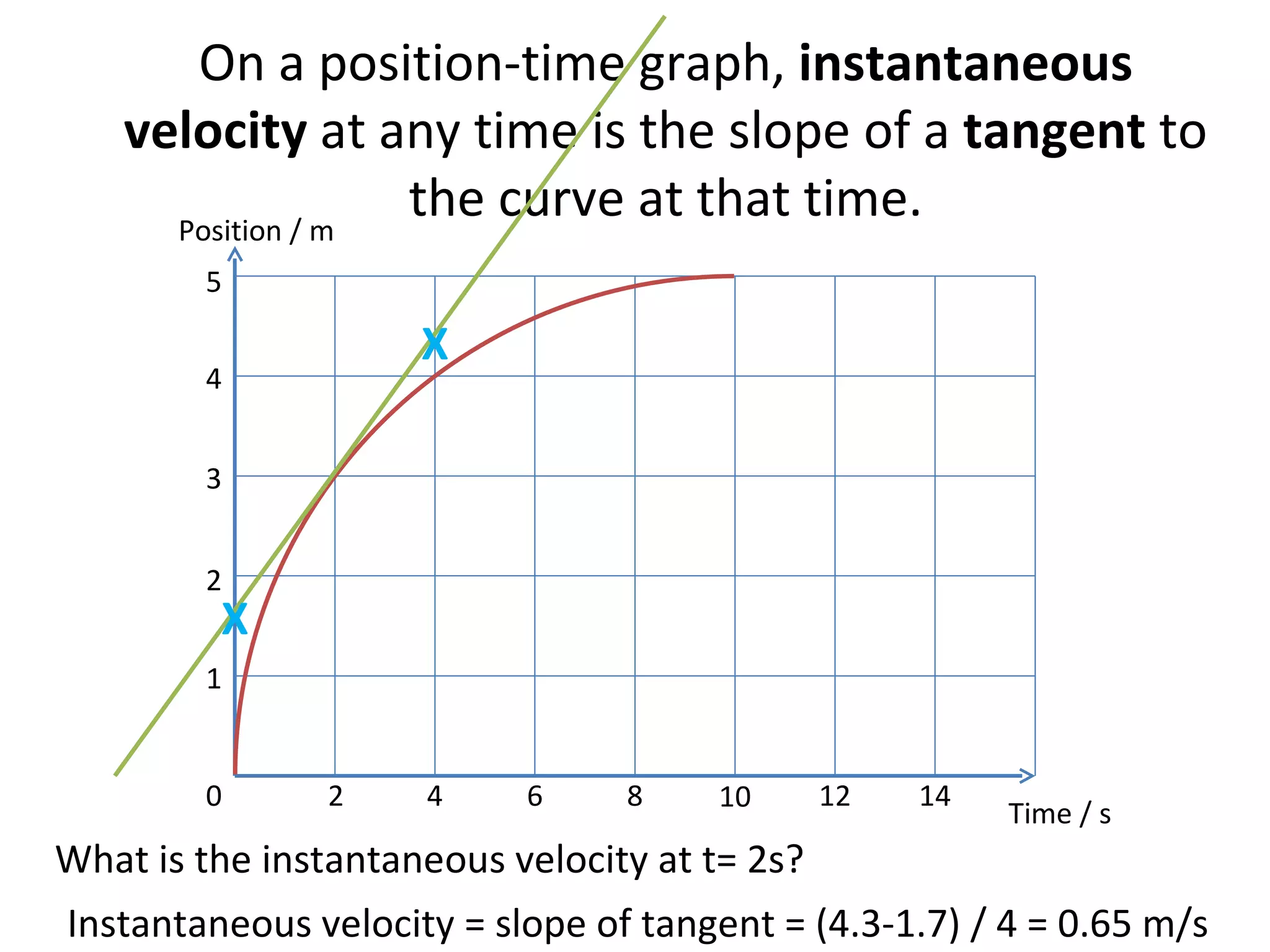
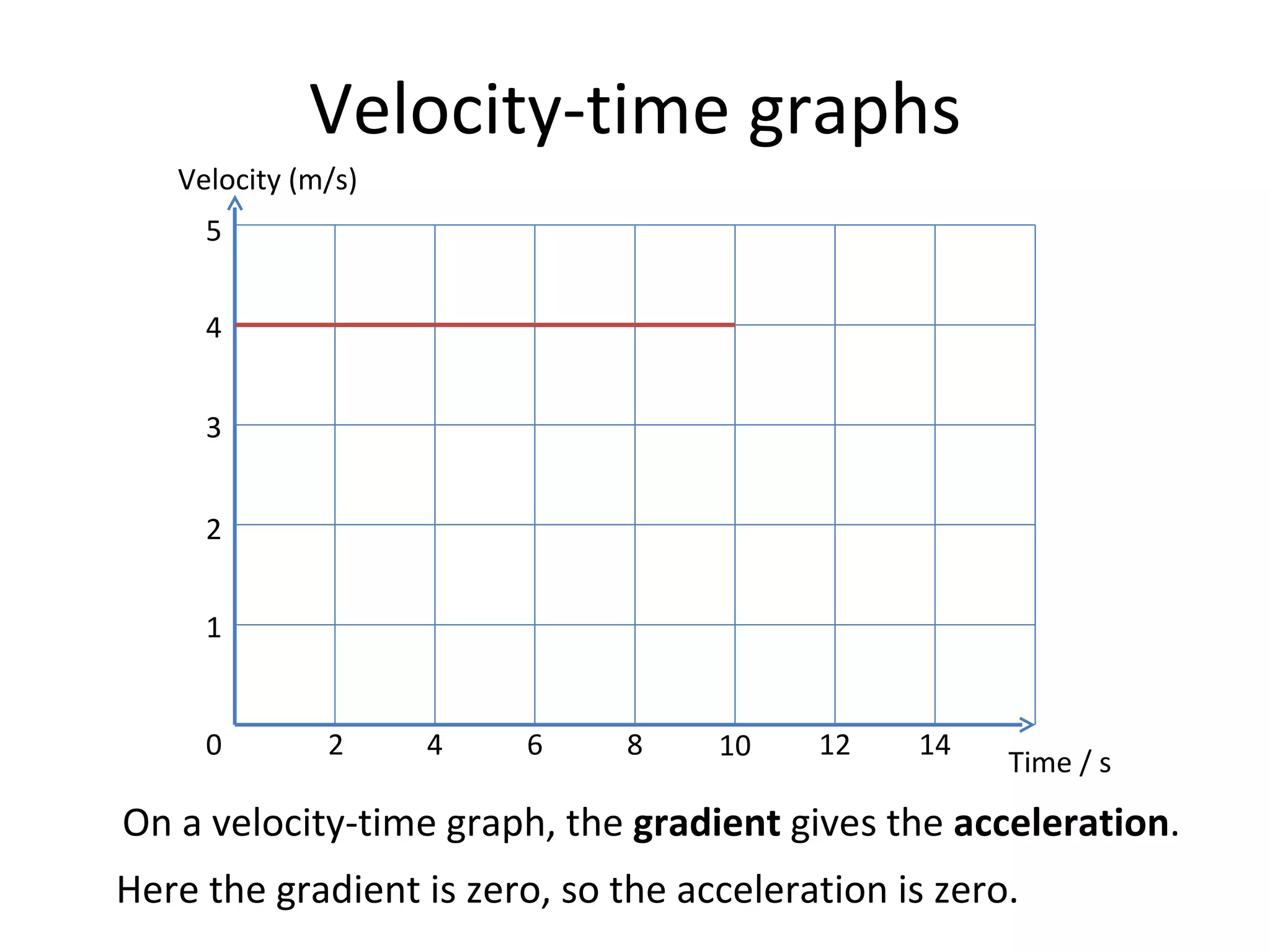
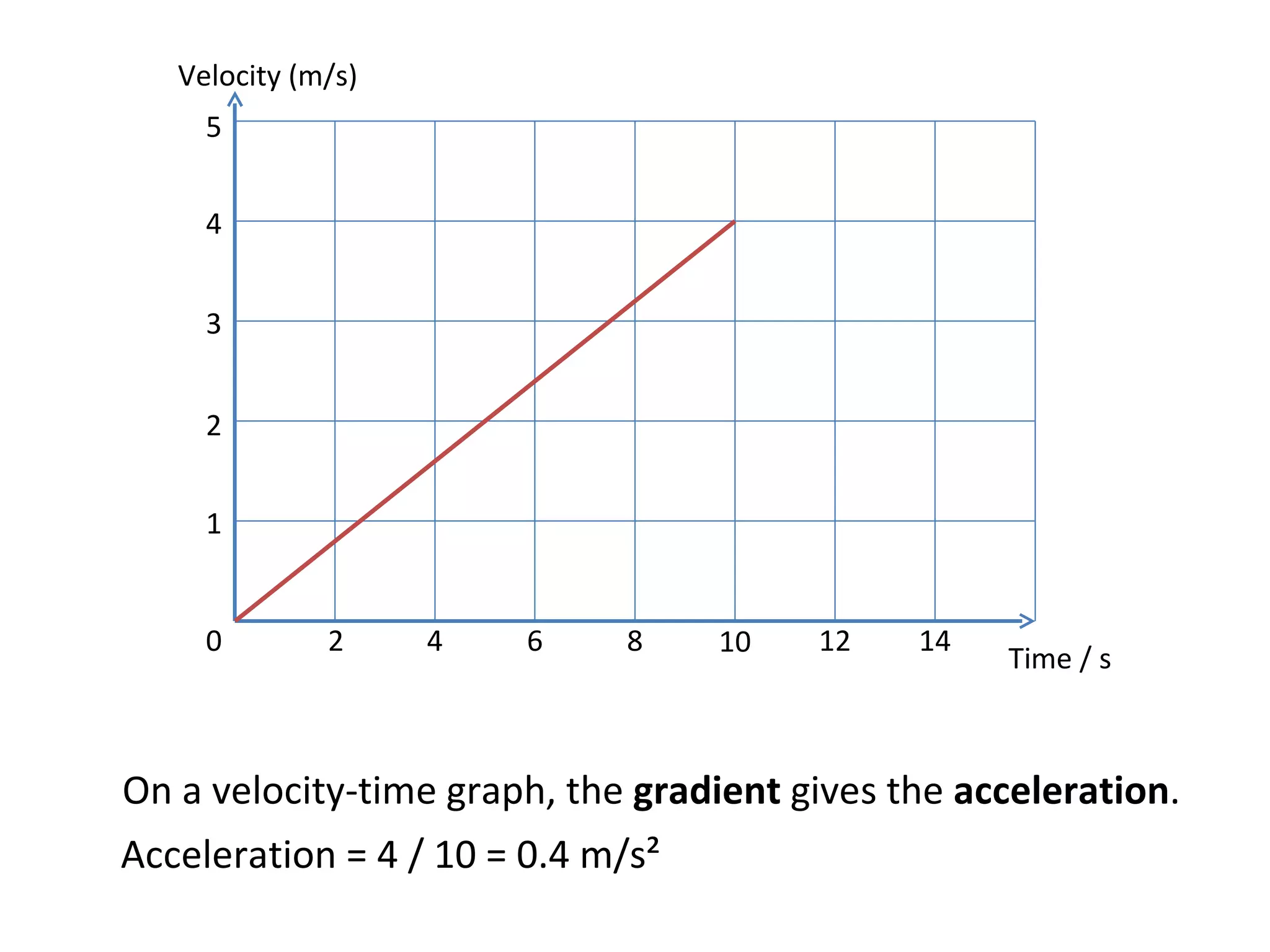
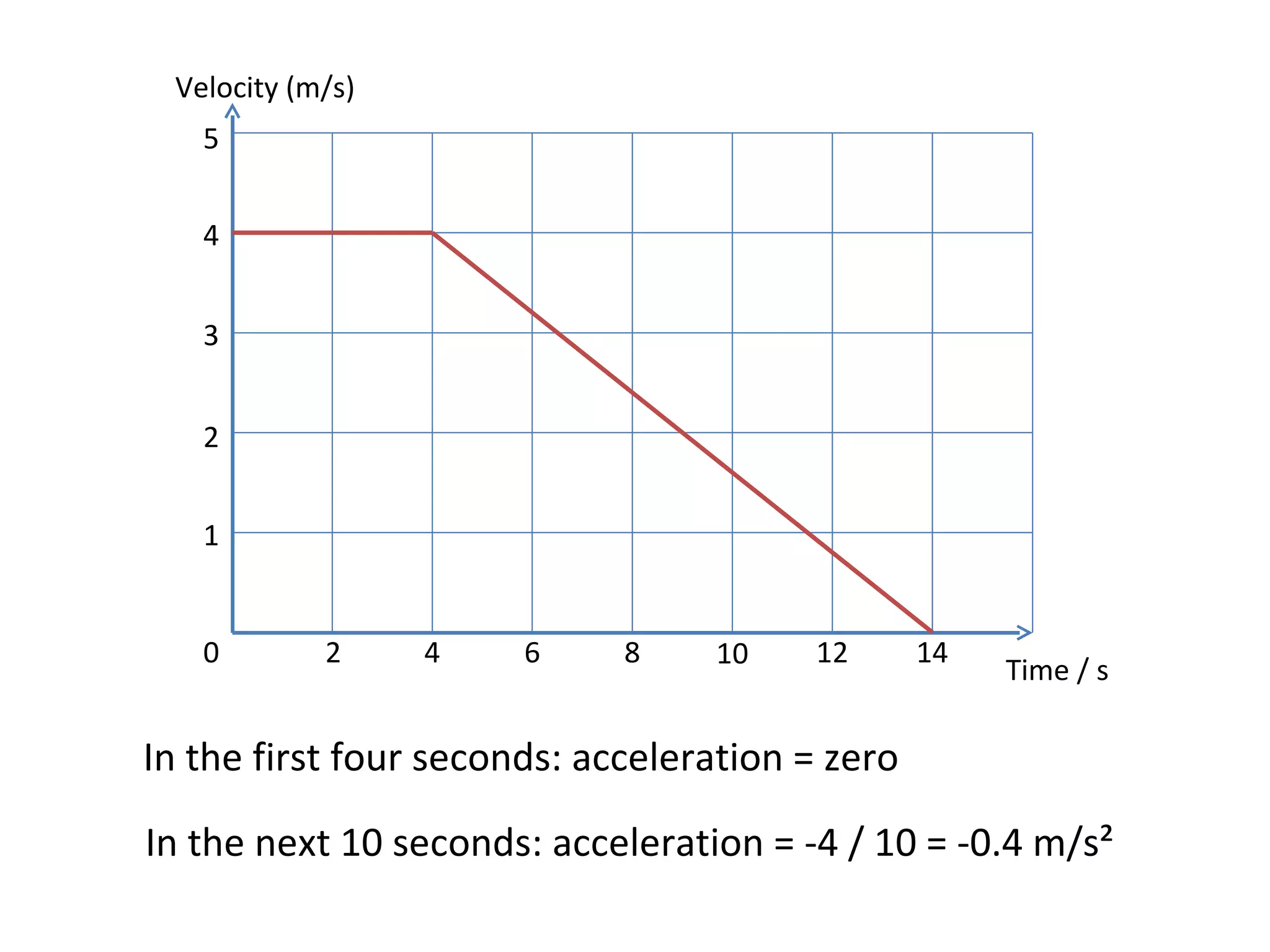
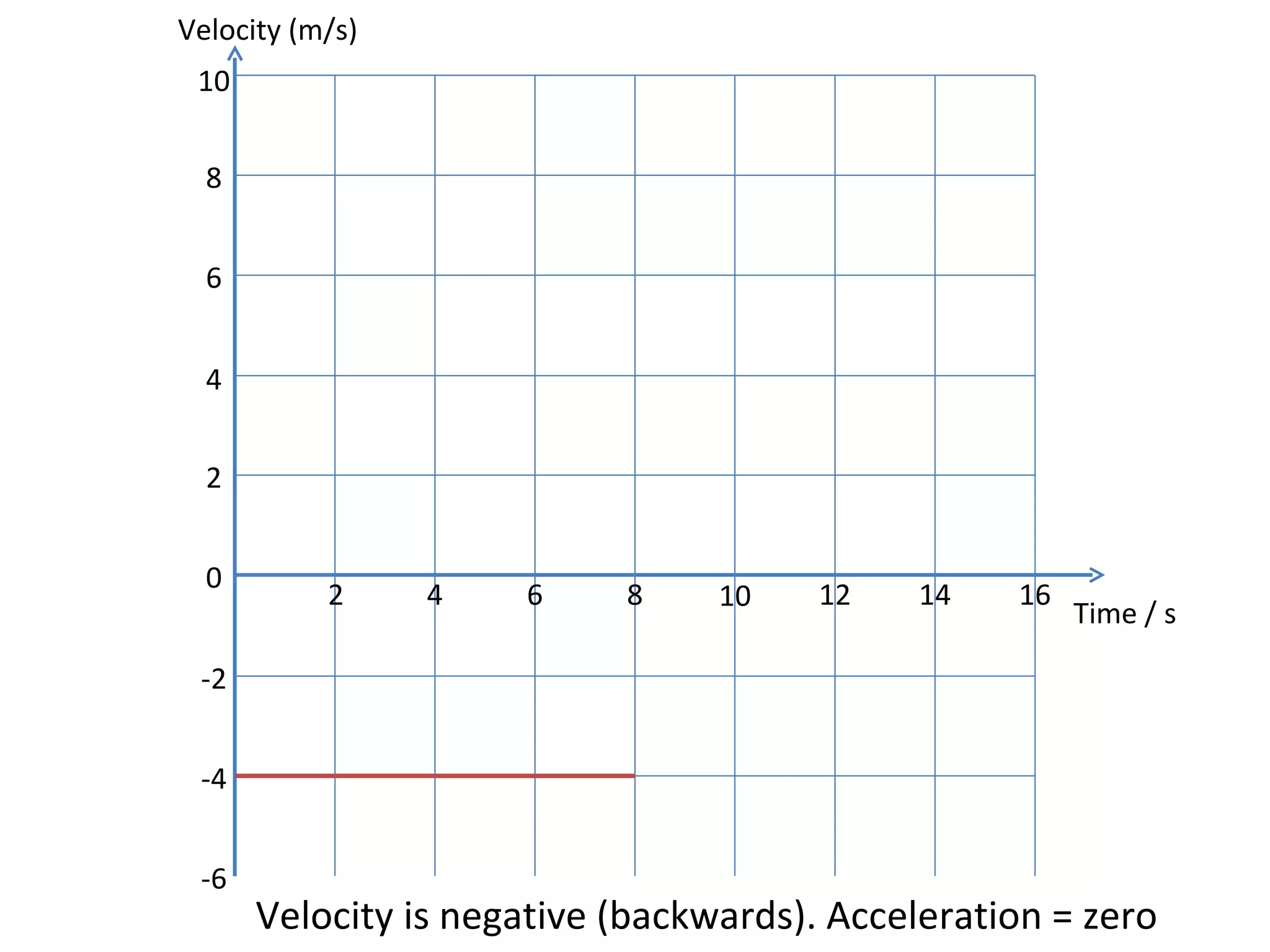
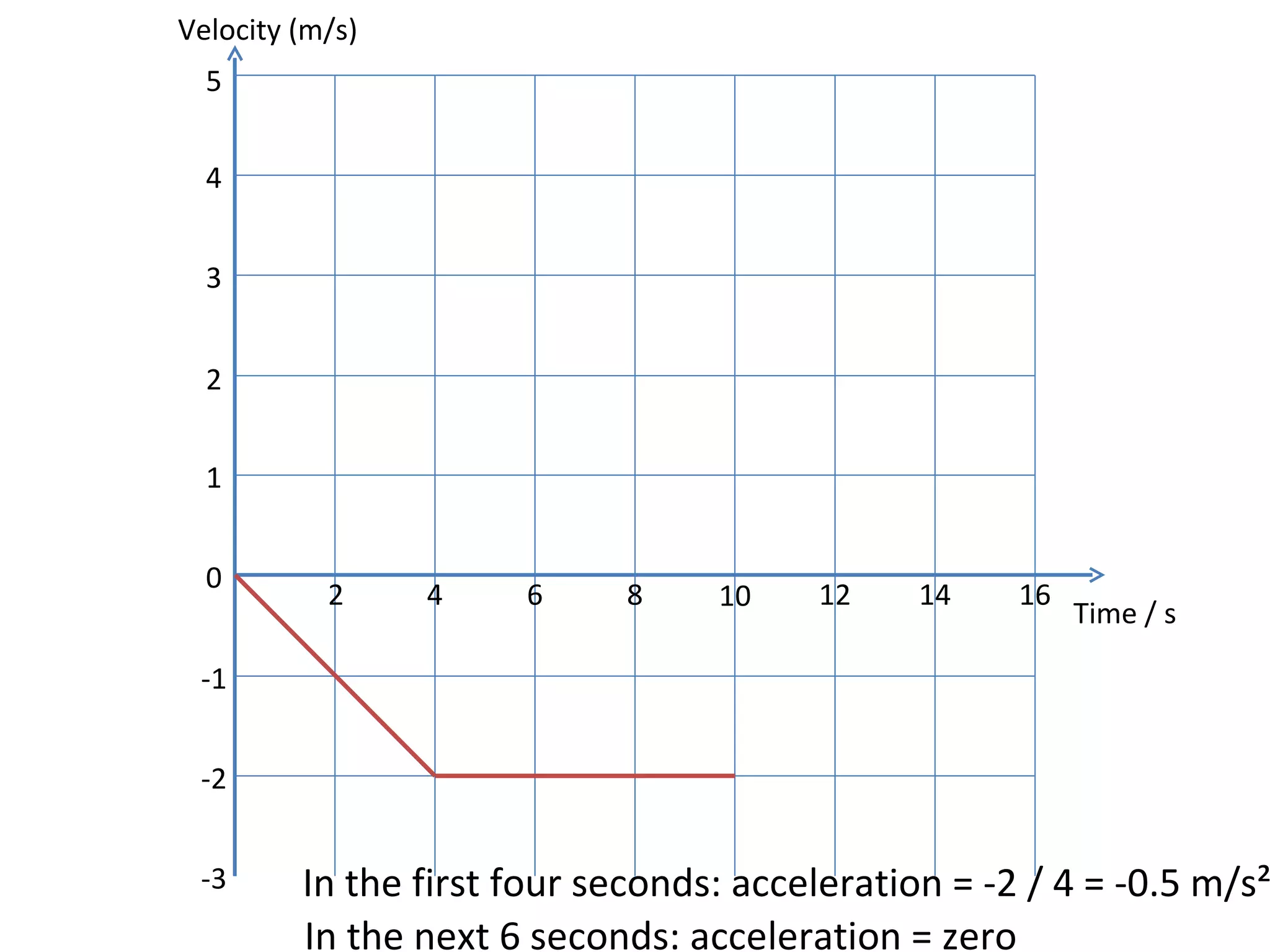
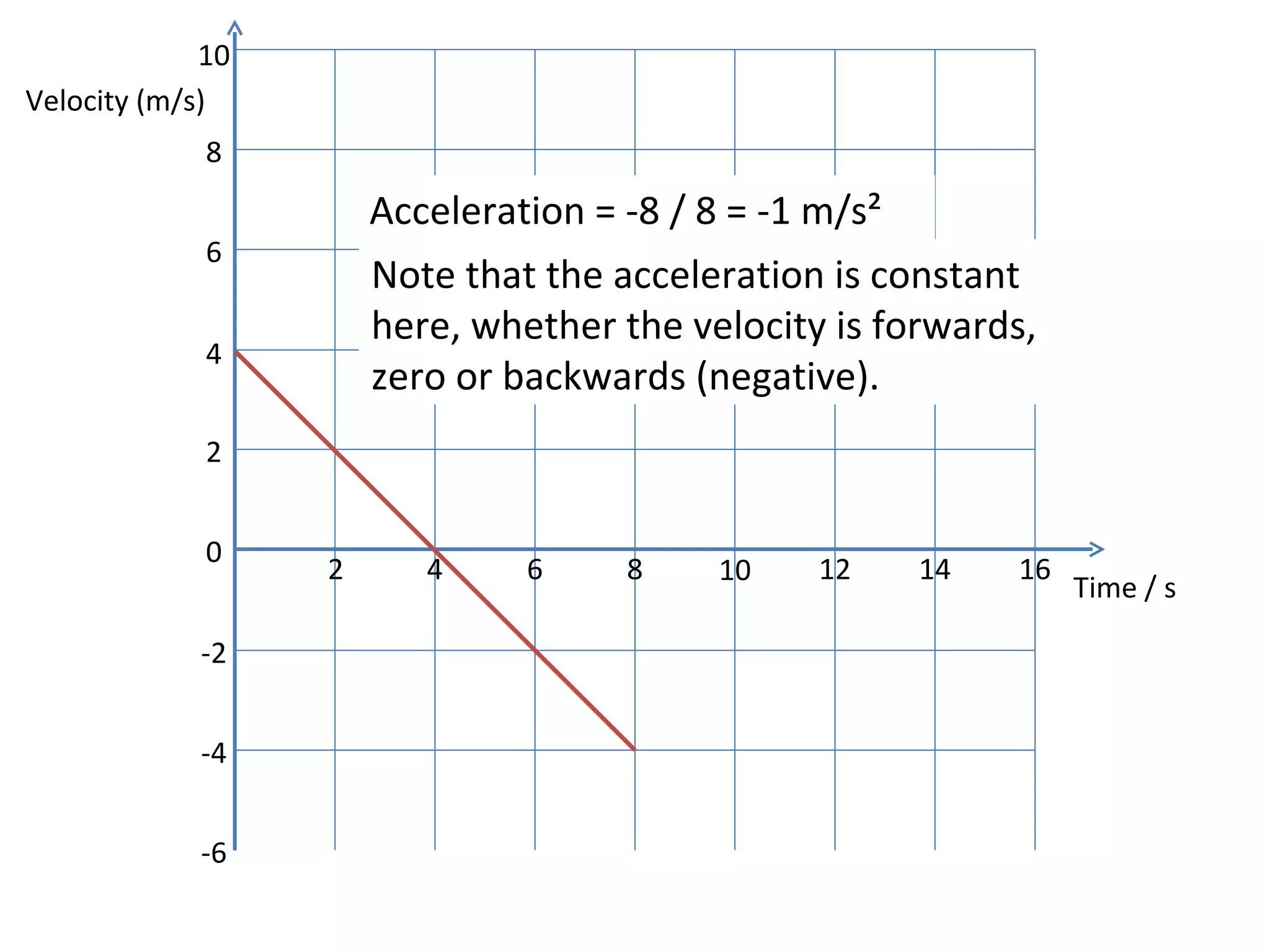
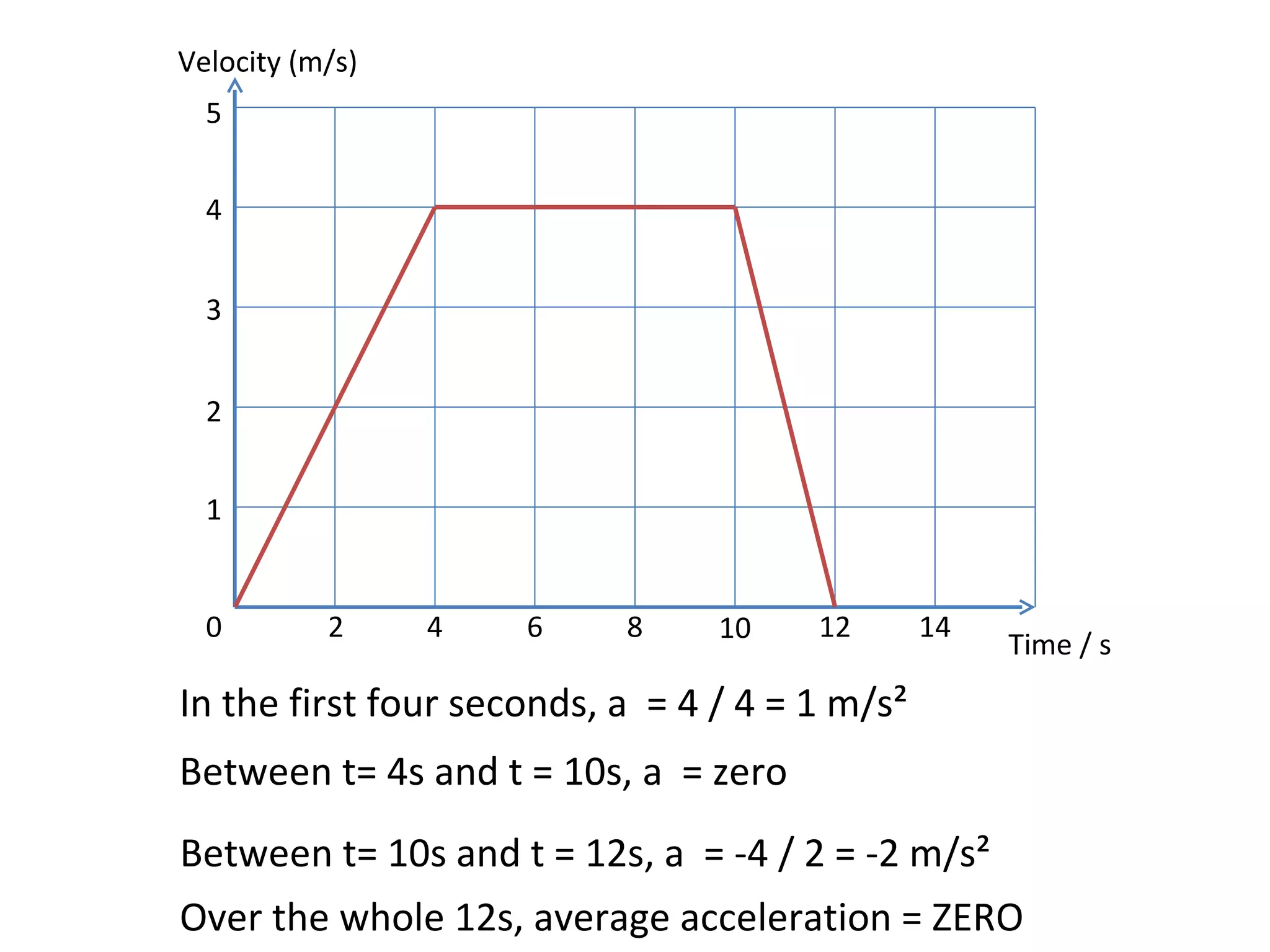
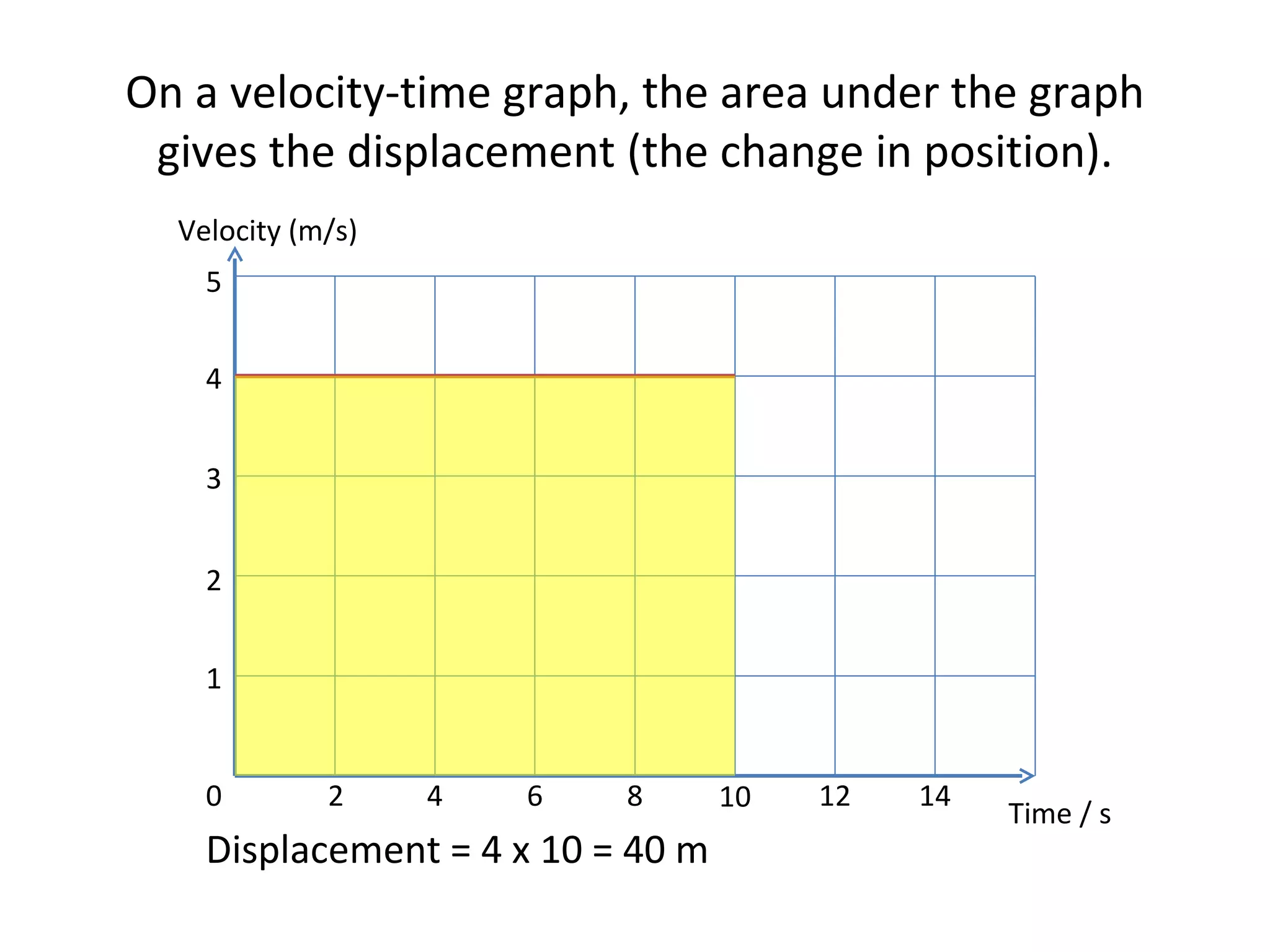
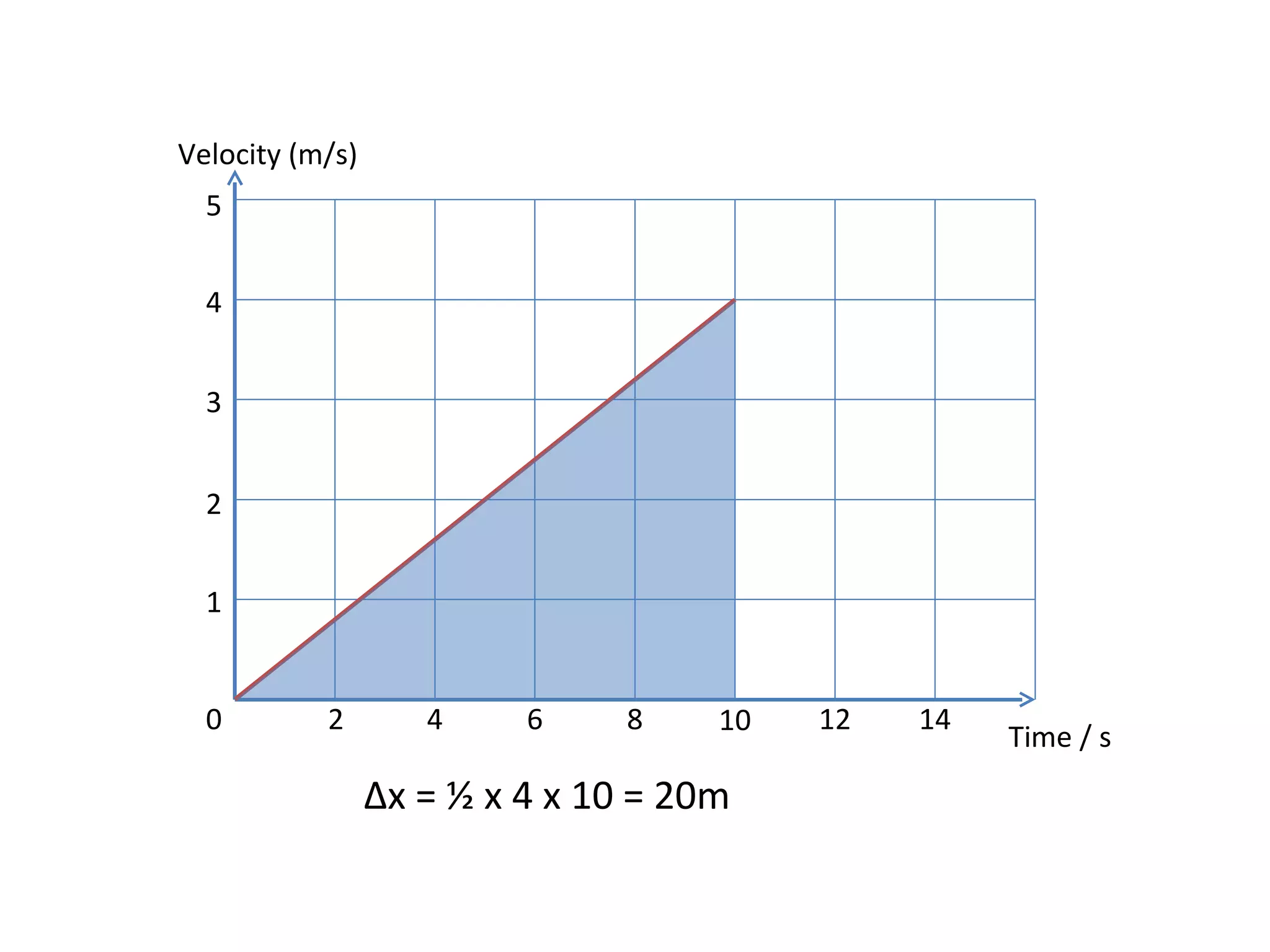
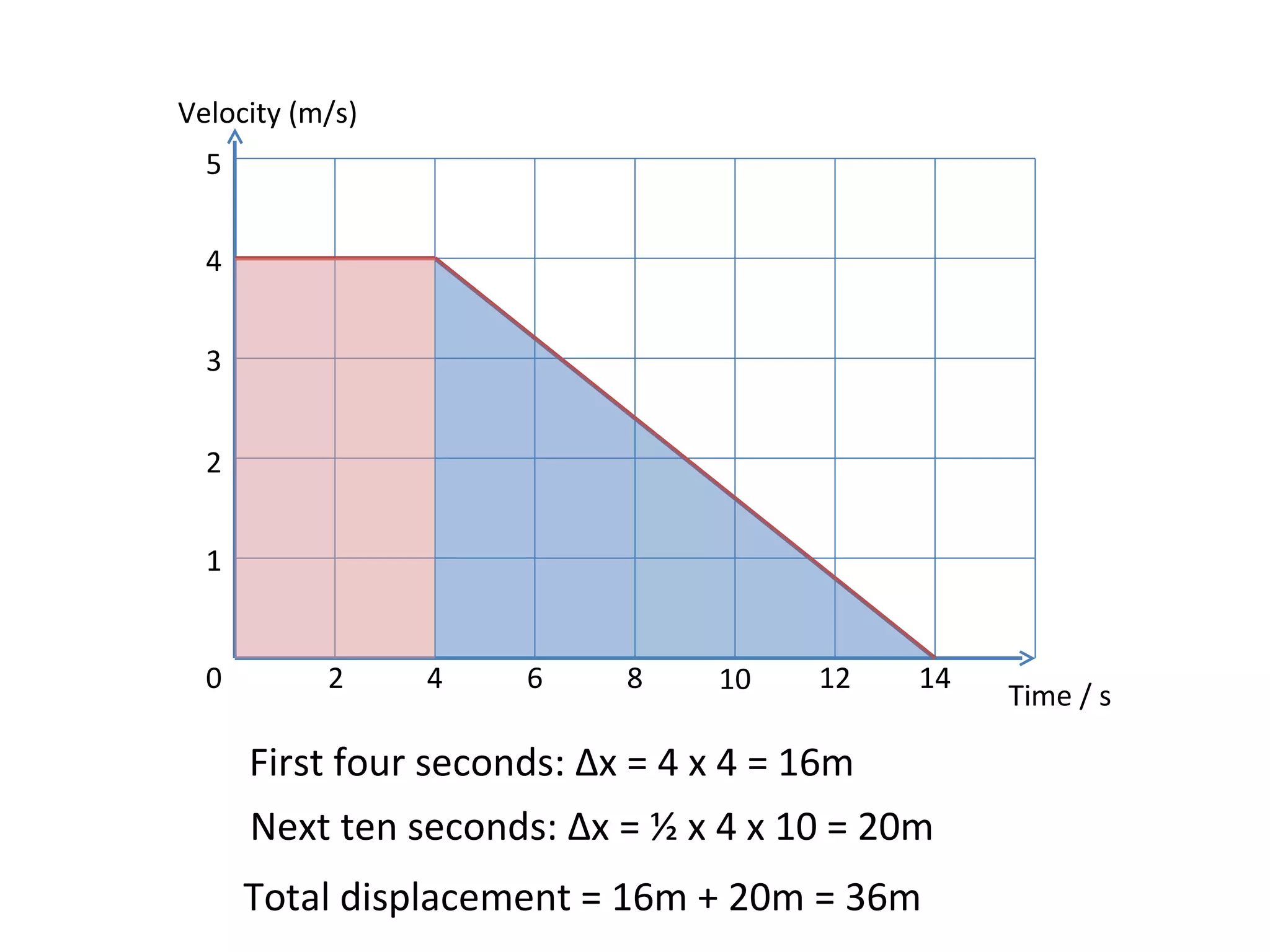
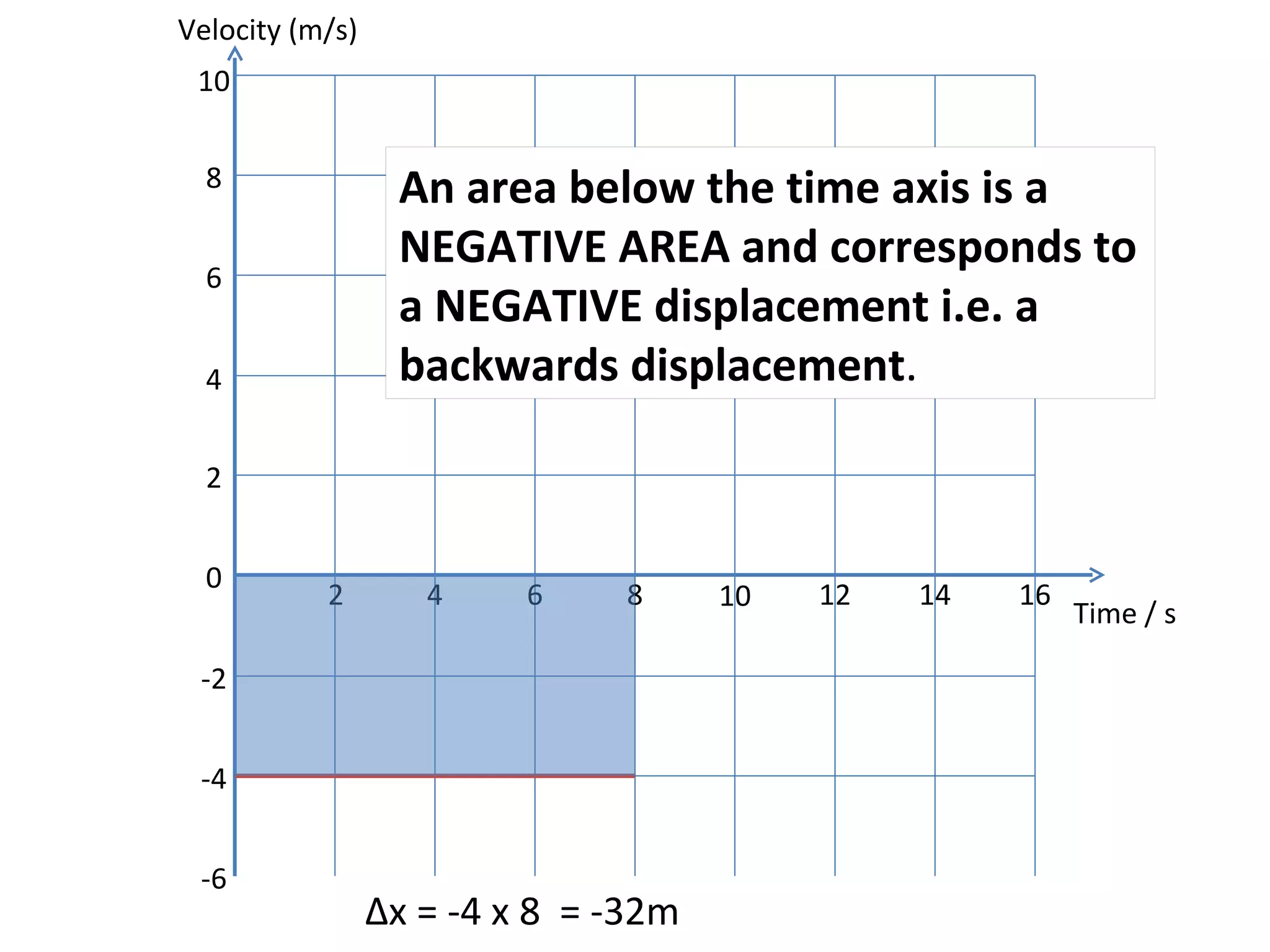
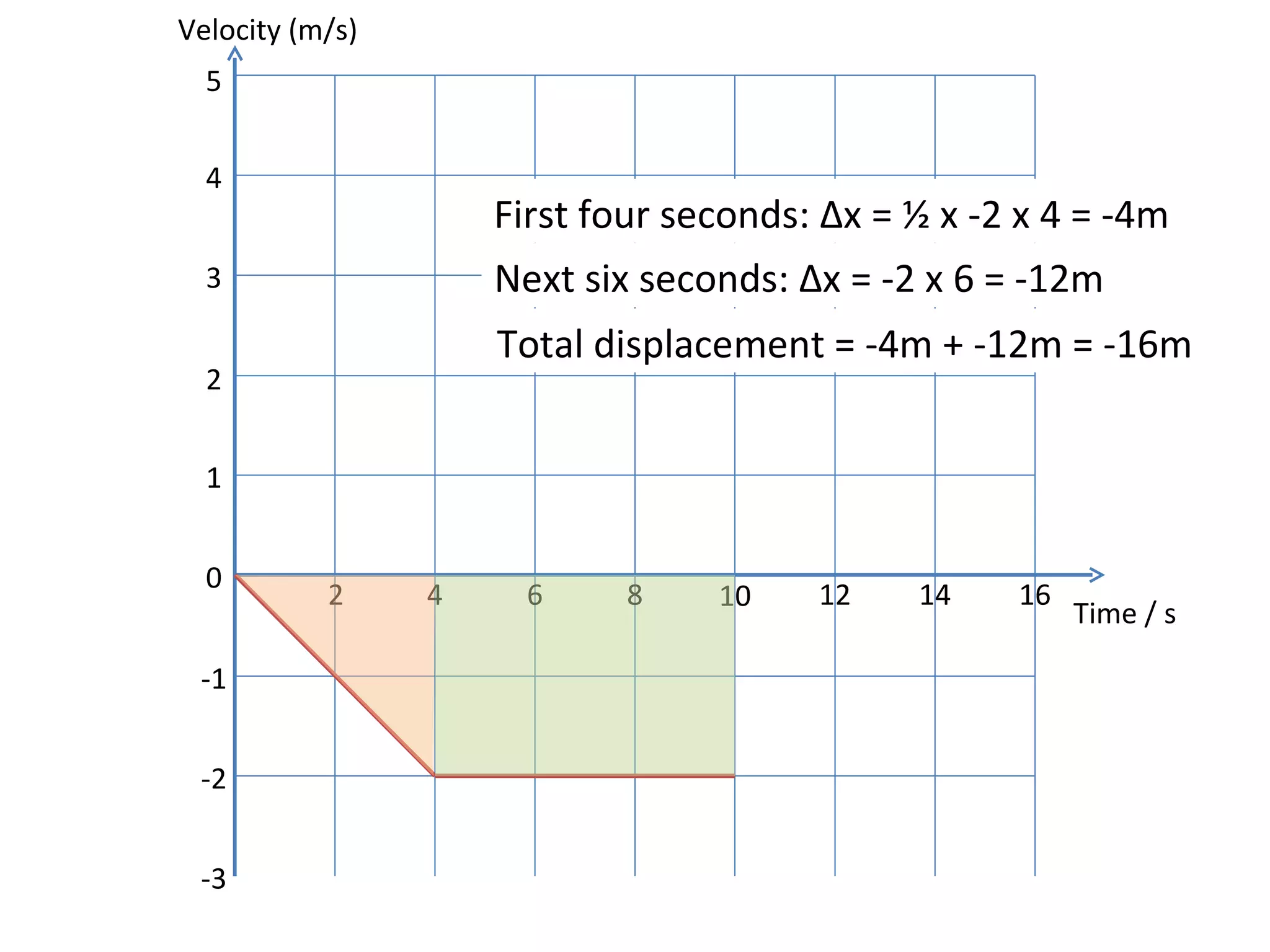
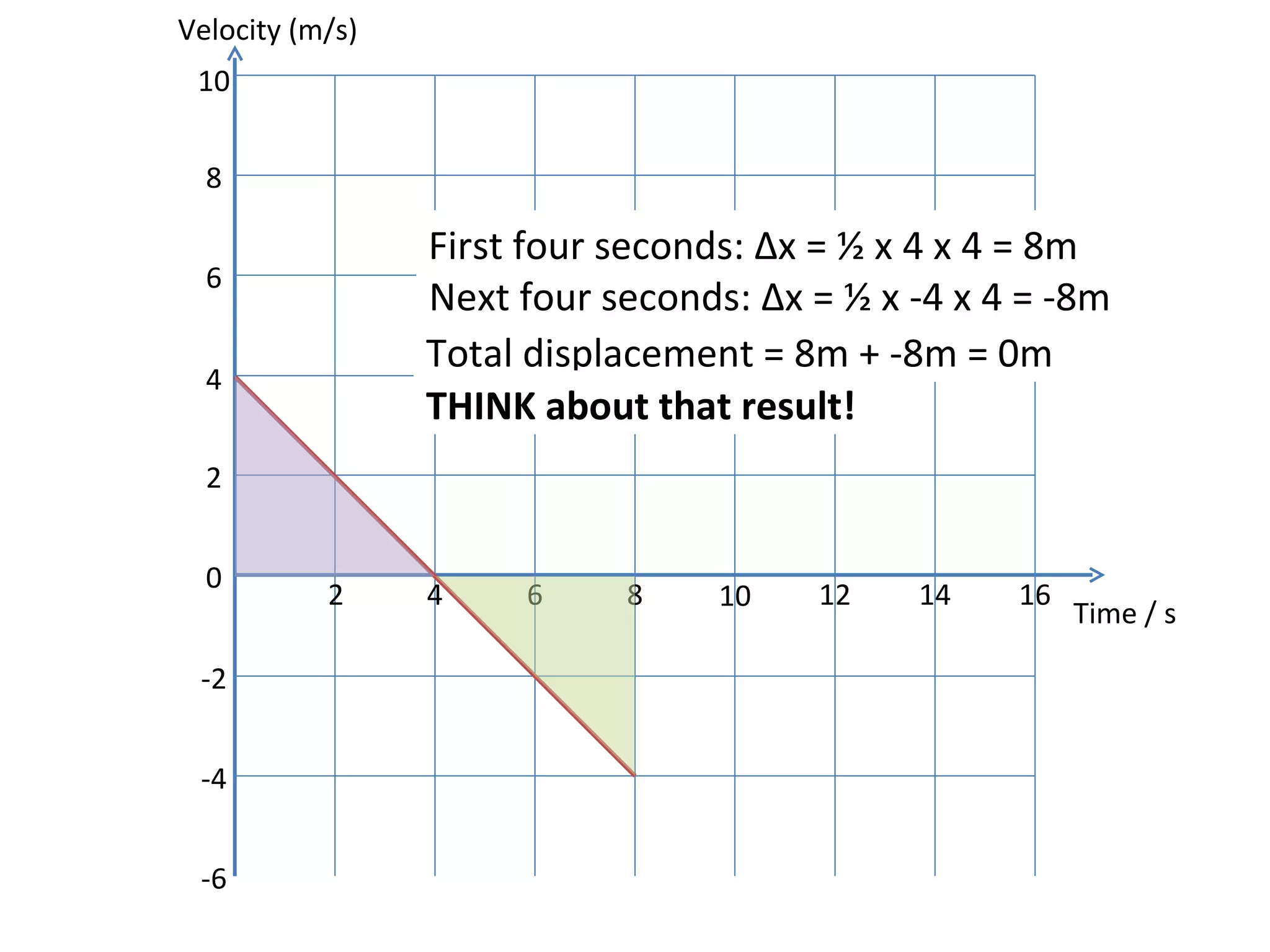
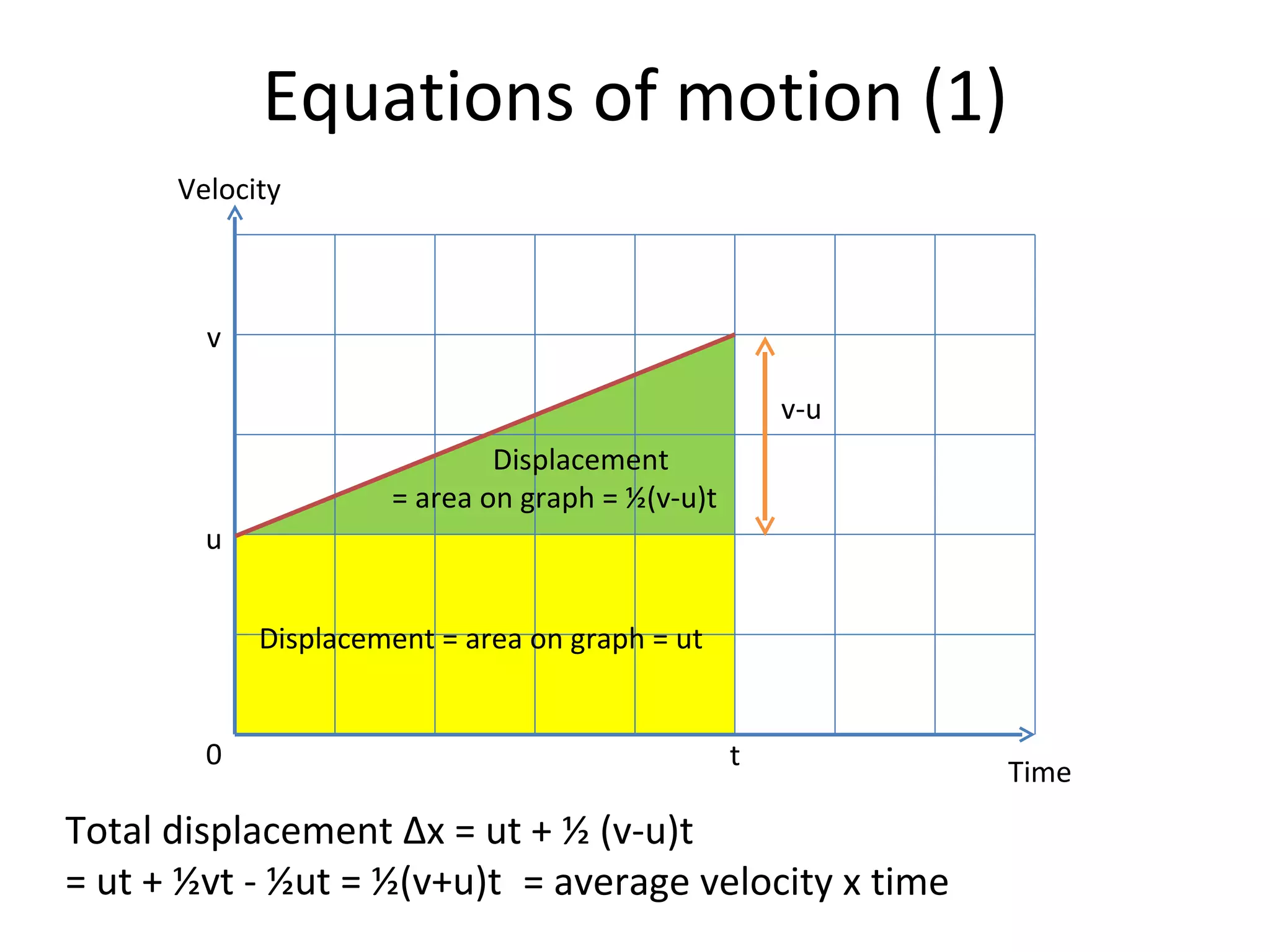
This document covers the basics of one-dimensional (linear) motion, emphasizing the importance of position-time and velocity-time graphs. Key concepts include calculating velocity from gradients, understanding instantaneous velocity, and using area under the curve to find displacement. The document also presents equations of motion and guides the reader on selecting the appropriate equation based on given variables.