This document contains lecture notes on inverse trigonometric functions. It begins with definitions of inverse functions and conditions for a function to have an inverse. It then defines the inverse trigonometric functions arcsin, arccos, arctan, and arcsec and gives their domains and ranges. Examples are provided to illustrate calculating values of the inverse trigonometric functions. The document concludes with a brief discussion of notational ambiguity and an outline mentioning that derivatives of the inverse trigonometric functions will be covered.

1. Section 3.5
Inverse Trigonometric
Functions
V63.0121.006/016, Calculus I
March 11, 2010
Announcements
Exams returned in recitation
There is WebAssign due Tuesday March 23 and written HW
due Thursday March 25 . . . . . .

2. Announcements
Exams returned in recitation
There is WebAssign due Tuesday March 23 and written HW
due Thursday March 25
next quiz is Friday April 2
. . . . . .

3. What is an inverse function?
Definition
Let f be a function with domain D and range E. The inverse of f is
the function f−1 defined by:
f−1 (b) = a,
where a is chosen so that f(a) = b.
. . . . . .

4. What is an inverse function?
Definition
Let f be a function with domain D and range E. The inverse of f is
the function f−1 defined by:
f−1 (b) = a,
where a is chosen so that f(a) = b.
So
f−1 (f(x)) = x, f(f−1 (x)) = x
. . . . . .

5. What functions are invertible?
In order for f−1 to be a function, there must be only one a in D
corresponding to each b in E.
Such a function is called one-to-one
The graph of such a function passes the horizontal line test:
any horizontal line intersects the graph in exactly one point
if at all.
If f is continuous, then f−1 is continuous.
. . . . . .

6. Outline
Inverse Trigonometric Functions
Derivatives of Inverse Trigonometric Functions
Arcsine
Arccosine
Arctangent
Arcsecant
Applications
. . . . . .

7. arcsin
Arcsin is the inverse of the sine function after restriction to
[−π/2, π/2].
y
.
. . . x
.
π π s
. in
−
. .
2 2
. . . . . .

8. arcsin
Arcsin is the inverse of the sine function after restriction to
[−π/2, π/2].
y
.
.
. . . x
.
π π s
. in
−
. . .
2 2
. . . . . .

9. arcsin
Arcsin is the inverse of the sine function after restriction to
[−π/2, π/2].
y
.
y
. =x
.
. . . x
.
π π s
. in
−
. . .
2 2
. . . . . .

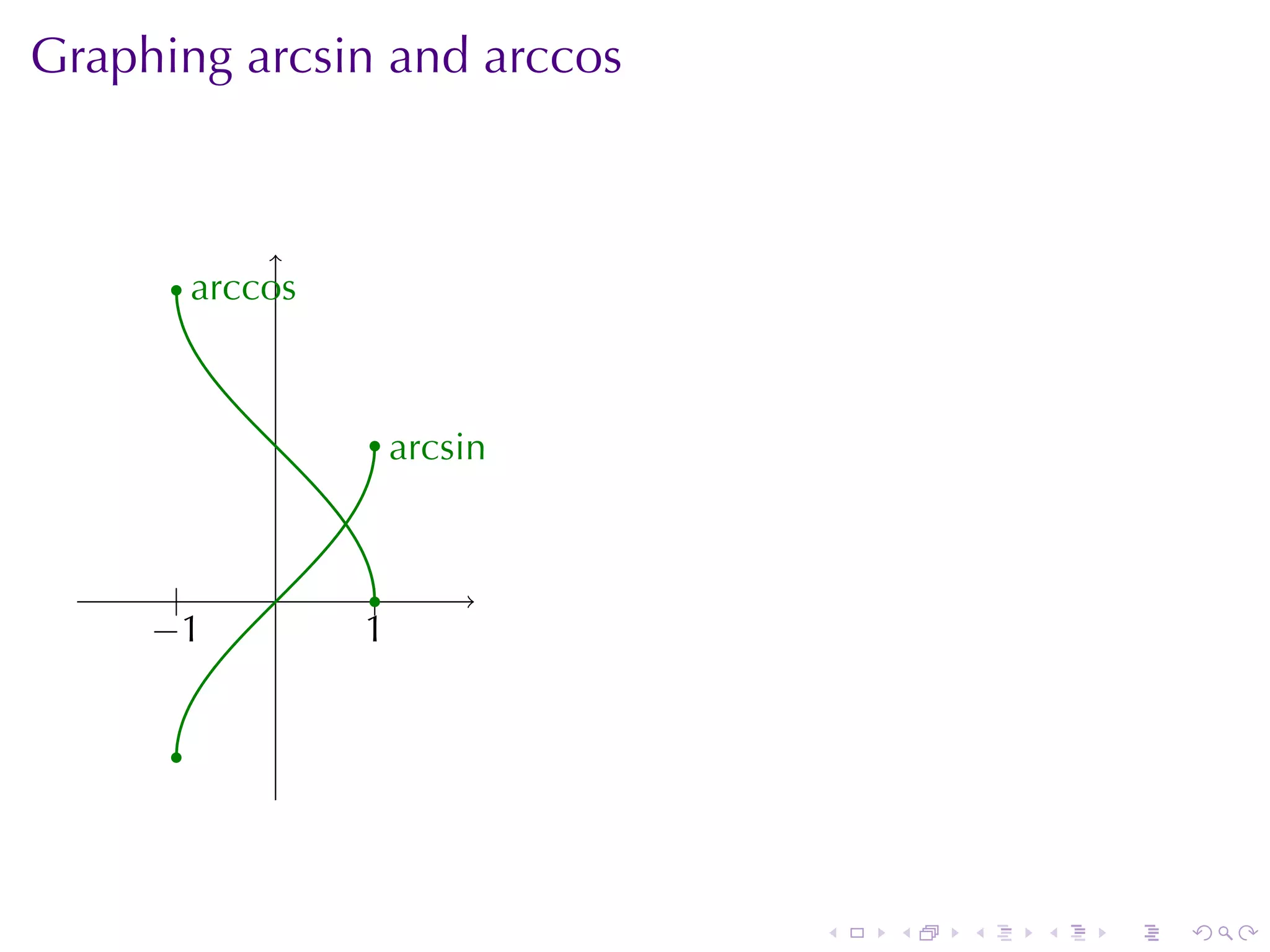
10. arcsin
Arcsin is the inverse of the sine function after restriction to
[−π/2, π/2].
y
.
. . rcsin
a
.
. . . x
.
π π s
. in
−
. . .
2 2
.
The domain of arcsin is [−1, 1]
[ π π]
The range of arcsin is − ,
2 2
. . . . . .

11. arccos
Arccos is the inverse of the cosine function after restriction to
[0, π]
y
.
c
. os
. . x
.
0
. .
π
. . . . . .

12. arccos
Arccos is the inverse of the cosine function after restriction to
[0, π]
y
.
.
c
. os
. . x
.
0
. .
π
.
. . . . . .

13. arccos
Arccos is the inverse of the cosine function after restriction to
[0, π]
y
.
y
. =x
.
c
. os
. . x
.
0
. .
π
.
. . . . . .

14. arccos
Arccos is the inverse of the cosine function after restriction to
[0, π]
. . rccos
a
y
.
.
c
. os
. . . x
.
0
. .
π
.
The domain of arccos is [−1, 1]
The range of arccos is [0, π]
. . . . . .

15. arctan
Arctan is the inverse of the tangent function after restriction to
[−π/2, π/2].
y
.
. x
.
3π π π 3π
−
. −
. . .
2 2 2 2
t
.an
. . . . . .

16. arctan
Arctan is the inverse of the tangent function after restriction to
[−π/2, π/2].
y
.
. x
.
3π π π 3π
−
. −
. . .
2 2 2 2
t
.an
. . . . . .

17. arctan
Arctan is the inverse of the tangent function after restriction to
y
. =x
[−π/2, π/2].
y
.
. x
.
3π π π 3π
−
. −
. . .
2 2 2 2
t
.an
. . . . . .

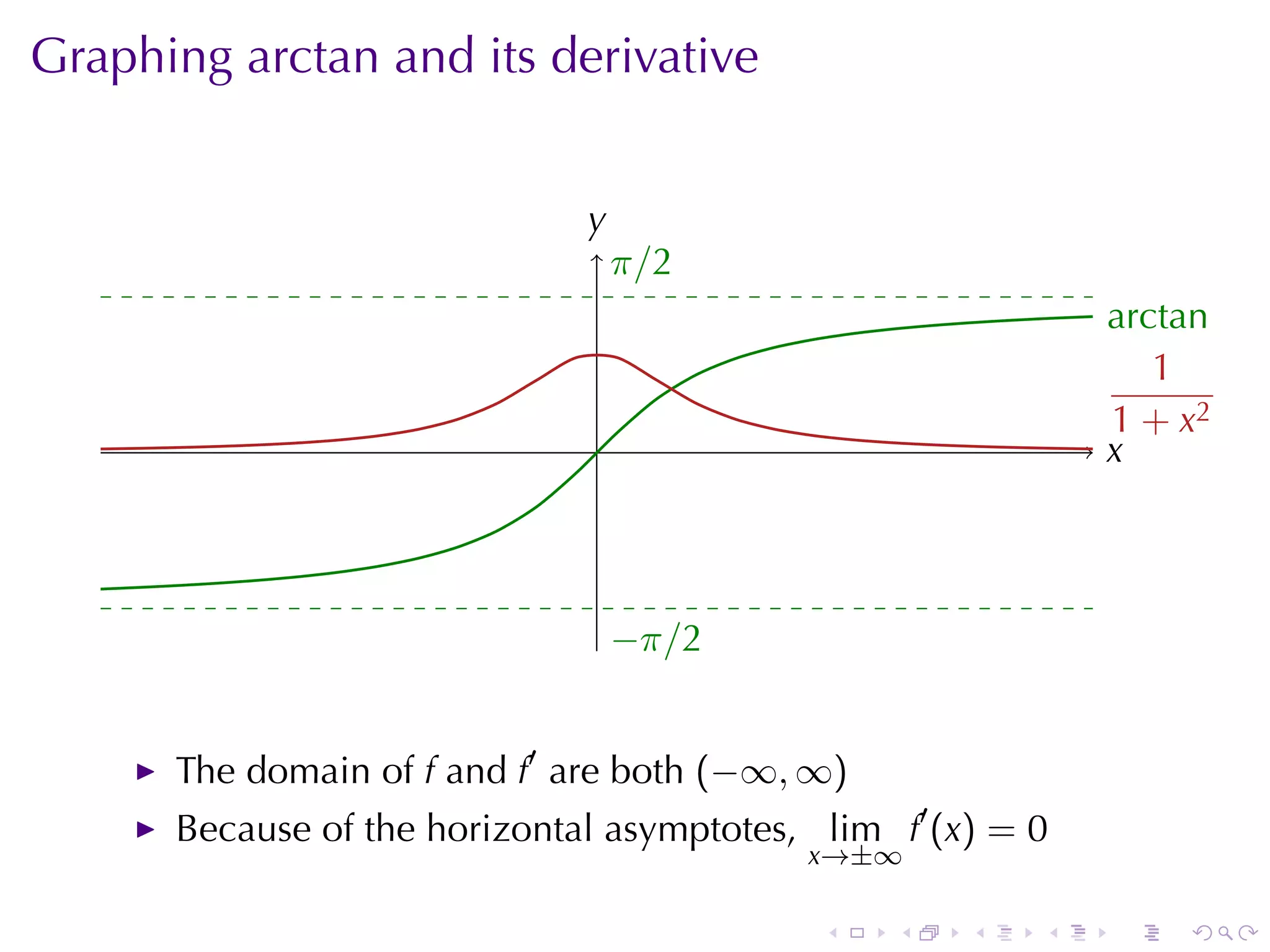
18. arctan
Arctan is the inverse of the tangent function after restriction to
[−π/2, π/2].
y
.
π
. a
. rctan
2
. x
.
π
−
.
2
The domain of arctan is (−∞, ∞)
( π π)
The range of arctan is − ,
2 2
π π
lim arctan x = , lim arctan x = −
x→∞ 2 x→−∞ 2
. . . . . .

19. arcsec
Arcsecant is the inverse of secant after restriction to
[0, π/2) ∪ (π, 3π/2].
y
.
. x
.
3π π π 3π
−
. −
. . .
2 2 2 2
s
. ec
. . . . . .

20. arcsec
Arcsecant is the inverse of secant after restriction to
[0, π/2) ∪ (π, 3π/2].
y
.
.
. x
.
3π π π 3π
−
. −
. . . .
2 2 2 2
s
. ec
. . . . . .

21. arcsec
Arcsecant is the inverse of secant after restriction to
y
. =x
[0, π/2) ∪ (π, 3π/2].
y
.
.
. x
.
3π π π 3π
−
. −
. . . .
2 2 2 2
s
. ec
. . . . . .

22. arcsec 3π
.
Arcsecant is the inverse of secant after restriction to
2
[0, π/2) ∪ (π, 3π/2].
. . y
π
.
2 .
. . x
.
.
The domain of arcsec is (−∞, −1] ∪ [1, ∞)
[ π ) (π ]
The range of arcsec is 0, ∪ ,π
2 2
π 3π
lim arcsec x = , lim arcsec x =
x→∞ 2 x→−∞ 2
. . . . . .

23. Values of Trigonometric Functions
π π π π
x 0
6 4 3 2
√ √
1 2 3
sin x 0 1
2 2 2
√ √
3 2 1
cos x 1 0
2 2 2
1 √
tan x 0 √ 1 3 undef
3
√ 1
cot x undef 3 1 √ 0
3
2 2
sec x 1 √ √ 2 undef
3 2
2 2
csc x undef 2 √ √ 1
2 3
. . . . . .

24. Check: Values of inverse trigonometric functions
Example
Find
arcsin(1/2)
arctan(−1)
( √ )
2
arccos −
2
. . . . . .

25. Check: Values of inverse trigonometric functions
Example
Find
arcsin(1/2)
arctan(−1)
( √ )
2
arccos −
2
Solution
π
6
. . . . . .

26. What is arctan(−1)?
.
3
. π/4
.
. .
.
−
. π/4
. . . . . .

27. What is arctan(−1)?
.
( )
3
. π/4 3π
. Yes, tan = −1
4
√
2
s
. in(3π/4) =
2
.
√ .
2
. os(3π/4) = −
c
2
.
−
. π/4
. . . . . .

28. What is arctan(−1)?
.
( )
3
. π/4 3π
. Yes, tan = −1
4
√ But, the range of arctan
( π π)
2
s
. in(3π/4) = is − ,
2 2 2
.
√ .
2
. os(3π/4) = −
c
2
.
−
. π/4
. . . . . .

29. What is arctan(−1)?
.
( )
3
. π/4 3π
. Yes, tan = −1
4
But, the range of arctan
( π π)
√ is − ,
2 2 2
c
. os(π/4) =
. 2 Another angle whose
. π
tangent is −1 is − , and
√ 4
2 this is in the right range.
. in(π/4) = −
s
2
.
−
. π/4
. . . . . .

30. What is arctan(−1)?
.
( )
3
. π/4 3π
. Yes, tan = −1
4
But, the range of arctan
( π π)
√ is − ,
2 2 2
c
. os(π/4) =
. 2 Another angle whose
. π
tangent is −1 is − , and
√ 4
2 this is in the right range.
. in(π/4) = −
s π
2 So arctan(−1) = −
4
.
−
. π/4
. . . . . .

31. Check: Values of inverse trigonometric functions
Example
Find
arcsin(1/2)
arctan(−1)
( √ )
2
arccos −
2
Solution
π
6
π
−
4
. . . . . .

32. Check: Values of inverse trigonometric functions
Example
Find
arcsin(1/2)
arctan(−1)
( √ )
2
arccos −
2
Solution
π
6
π
−
4
3π
4
. . . . . .

33. Caution: Notational ambiguity
. in2 x =.(sin x)2
s . in−1 x = (sin x)−1
s
sinn x means the nth power of sin x, except when n = −1!
The book uses sin−1 x for the inverse of sin x, and never for
(sin x)−1 .
1
I use csc x for and arcsin x for the inverse of sin x.
sin x
. . . . . .

34. Outline
Inverse Trigonometric Functions
Derivatives of Inverse Trigonometric Functions
Arcsine
Arccosine
Arctangent
Arcsecant
Applications
. . . . . .

35. Theorem (The Inverse Function Theorem)
Let f be differentiable at a, and f′ (a) ̸= 0. Then f−1 is defined in an
open interval containing b = f(a), and
1
(f−1 )′ (b) = ′ −1
f (f (b))
. . . . . .

36. Theorem (The Inverse Function Theorem)
Let f be differentiable at a, and f′ (a) ̸= 0. Then f−1 is defined in an
open interval containing b = f(a), and
1
(f−1 )′ (b) = ′ −1
f (f (b))
“Proof”.
If y = f−1 (x), then
f(y ) = x ,
So by implicit differentiation
dy dy 1 1
f′ (y) = 1 =⇒ = ′ = ′ −1
dx dx f (y) f (f (x))
. . . . . .

37. The derivative of arcsin
Let y = arcsin x, so x = sin y. Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)
. . . . . .

38. The derivative of arcsin
Let y = arcsin x, so x = sin y. Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)
To simplify, look at a right
triangle:
.
. . . . . .

39. The derivative of arcsin
Let y = arcsin x, so x = sin y. Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)
To simplify, look at a right
triangle:
1
.
x
.
.
. . . . . .

40. The derivative of arcsin
Let y = arcsin x, so x = sin y. Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)
To simplify, look at a right
triangle:
1
.
x
.
y
. = arcsin x
.
. . . . . .

41. The derivative of arcsin
Let y = arcsin x, so x = sin y. Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)
To simplify, look at a right
triangle:
1
.
x
.
y
. = arcsin x
. √
. 1 − x2
. . . . . .

42. The derivative of arcsin
Let y = arcsin x, so x = sin y. Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)
To simplify, look at a right
triangle:
√
cos(arcsin x) = 1 − x2 1
.
x
.
y
. = arcsin x
. √
. 1 − x2
. . . . . .

43. The derivative of arcsin
Let y = arcsin x, so x = sin y. Then
dy dy 1 1
cos y = 1 =⇒ = =
dx dx cos y cos(arcsin x)
To simplify, look at a right
triangle:
√
cos(arcsin x) = 1 − x2 1
.
x
.
So
d 1 y
. = arcsin x
arcsin(x) = √
dx 1 − x2 . √
. 1 − x2
. . . . . .

44. Graphing arcsin and its derivative
1
.√
1 − x2
The domain of f is
[−1, 1], but the domain . . rcsin
a
of f′ is (−1, 1)
lim f′ (x) = +∞
x →1 −
lim f′ (x) = +∞ .
| . .
|
x→−1+ −
. 1 1
.
.
. . . . . .

45. The derivative of arccos
Let y = arccos x, so x = cos y. Then
dy dy 1 1
− sin y = 1 =⇒ = =
dx dx − sin y − sin(arccos x)
. . . . . .

46. The derivative of arccos
Let y = arccos x, so x = cos y. Then
dy dy 1 1
− sin y = 1 =⇒ = =
dx dx − sin y − sin(arccos x)
To simplify, look at a right
triangle:
√
sin(arccos x) = 1 − x2 1
. √
. 1 − x2
So
d 1 y
. = arccos x
arccos(x) = − √ .
dx 1 − x2 x
.
. . . . . .

47. Graphing arcsin and arccos
. . rccos
a
. . rcsin
a
.
| . |.
.
−
. 1 1
.
.
. . . . . .

48. Graphing arcsin and arccos
. . rccos
a
Note
(π )
cos θ = sin −θ
. . rcsin
a 2
π
=⇒ arccos x = − arcsin x
2
.
| . |.
. So it’s not a surprise that their
−
. 1 1
. derivatives are opposites.
.
. . . . . .

49. The derivative of arctan
Let y = arctan x, so x = tan y. Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y
. . . . . .

50. The derivative of arctan
Let y = arctan x, so x = tan y. Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y
To simplify, look at a right
triangle:
.
. . . . . .

51. The derivative of arctan
Let y = arctan x, so x = tan y. Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y
To simplify, look at a right
triangle:
x
.
.
1
.
. . . . . .

52. The derivative of arctan
Let y = arctan x, so x = tan y. Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y
To simplify, look at a right
triangle:
x
.
y
. = arctan x
.
1
.
. . . . . .

53. The derivative of arctan
Let y = arctan x, so x = tan y. Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y
To simplify, look at a right
triangle:
√
. 1 + x2 x
.
y
. = arctan x
.
1
.
. . . . . .

54. The derivative of arctan
Let y = arctan x, so x = tan y. Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y
To simplify, look at a right
triangle:
1
cos(arctan x) = √
1 + x2 √
. 1 + x2 x
.
y
. = arctan x
.
1
.
. . . . . .

55. The derivative of arctan
Let y = arctan x, so x = tan y. Then
dy dy 1
sec2 y = 1 =⇒ = = cos2 (arctan x)
dx dx sec2 y
To simplify, look at a right
triangle:
1
cos(arctan x) = √
1 + x2 √
. 1 + x2 x
.
So
d 1 y
. = arctan x
arctan(x) = .
dx 1 + x2
1
.
. . . . . .

56. Graphing arctan and its derivative
y
.
. /2
π
a
. rctan
1
.
1 + x2
. x
.
−
. π/2
The domain of f and f′ are both (−∞, ∞)
Because of the horizontal asymptotes, lim f′ (x) = 0
x→±∞
. . . . . .

57. Example
√
Let f(x) = arctan x. Find f′ (x).
. . . . . .

58. Example
√
Let f(x) = arctan x. Find f′ (x).
Solution
d √ 1 d√ 1 1
arctan x = (√ )2 x= · √
dx 1+ x dx 1+x 2 x
1
= √ √
2 x + 2x x
. . . . . .

59. The derivative of arcsec
Try this first.
. . . . . .

60. The derivative of arcsec
Try this first. Let y = arcsec x, so x = sec y. Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))
. . . . . .

61. The derivative of arcsec
Try this first. Let y = arcsec x, so x = sec y. Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))
To simplify, look at a right
triangle:
.
. . . . . .

62. The derivative of arcsec
Try this first. Let y = arcsec x, so x = sec y. Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))
To simplify, look at a right
triangle:
.
. . . . . .

63. The derivative of arcsec
Try this first. Let y = arcsec x, so x = sec y. Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))
To simplify, look at a right
triangle:
x
.
.
1
.
. . . . . .

64. The derivative of arcsec
Try this first. Let y = arcsec x, so x = sec y. Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))
To simplify, look at a right
triangle:
x
.
y
. = arcsec x
.
1
.
. . . . . .

65. The derivative of arcsec
Try this first. Let y = arcsec x, so x = sec y. Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))
To simplify, look at a right
triangle:
√
x2 − 1
tan(arcsec x) = √
1 x
. . x2 − 1
y
. = arcsec x
.
1
.
. . . . . .

66. The derivative of arcsec
Try this first. Let y = arcsec x, so x = sec y. Then
dy dy 1 1
sec y tan y = 1 =⇒ = =
dx dx sec y tan y x tan(arcsec(x))
To simplify, look at a right
triangle:
√
x2 − 1
tan(arcsec x) = √
1 x
. . x2 − 1
So
d 1 y
. = arcsec x
arcsec(x) = √ .
dx x x2 − 1
1
.
. . . . . .

67. Another Example
Example
Let f(x) = earcsec x . Find f′ (x).
. . . . . .

68. Another Example
Example
Let f(x) = earcsec x . Find f′ (x).
Solution
1
f′ (x) = earcsec x · √
x x2 − 1
. . . . . .

69. Outline
Inverse Trigonometric Functions
Derivatives of Inverse Trigonometric Functions
Arcsine
Arccosine
Arctangent
Arcsecant
Applications
. . . . . .

70. Application
Example
One of the guiding principles
of most sports is to “keep
your eye on the ball.” In
baseball, a batter stands 2 ft
away from home plate as a
pitch is thrown with a
velocity of 130 ft/sec (about
90 mph). At what rate does
the batter’s angle of gaze
need to change to follow the
ball as it crosses home plate?
. . . . . .

71. Let y(t) be the distance from the ball to home plate, and θ the
angle the batter’s eyes make with home plate while following the
ball. We know y′ = −130 and we want θ′ at the moment that
y = 0.
y
.
1
. 30 ft/sec
.
θ
.
. 2
. ft
. . . . . .

72. Let y(t) be the distance from the ball to home plate, and θ the
angle the batter’s eyes make with home plate while following the
ball. We know y′ = −130 and we want θ′ at the moment that
y = 0.
We have θ = arctan(y/2).
Thus
dθ 1 1 dy
= ·
2 2 dt
dt 1 + ( y /2 )
y
.
1
. 30 ft/sec
.
θ
.
. 2
. ft
. . . . . .

73. Let y(t) be the distance from the ball to home plate, and θ the
angle the batter’s eyes make with home plate while following the
ball. We know y′ = −130 and we want θ′ at the moment that
y = 0.
We have θ = arctan(y/2).
Thus
dθ 1 1 dy
= ·
2 2 dt
dt 1 + ( y /2 )
When y = 0 and y′ = −130, y
.
then
dθ 1 1
= · (−130) = −65 rad/sec 1
. 30 ft/sec
dt y =0 1+0 2
.
θ
.
. 2
. ft
. . . . . .

74. Let y(t) be the distance from the ball to home plate, and θ the
angle the batter’s eyes make with home plate while following the
ball. We know y′ = −130 and we want θ′ at the moment that
y = 0.
We have θ = arctan(y/2).
Thus
dθ 1 1 dy
= ·
2 2 dt
dt 1 + ( y /2 )
When y = 0 and y′ = −130, y
.
then
dθ 1 1
= · (−130) = −65 rad/sec 1
. 30 ft/sec
dt y =0 1+0 2
.
θ
The human eye can only .
track at 3 rad/sec! . 2
. ft
. . . . . .

75. Recap
y y′
1
arcsin x √
1 − x2
1
arccos x − √ Remarkable that the
1 − x2
derivatives of these
1 transcendental functions
arctan x
1 + x2 are algebraic (or even
1 rational!)
arccot x −
1 + x2
1
arcsec x √
x x2 − 1
1
arccsc x − √
x x2 − 1
. . . . . .