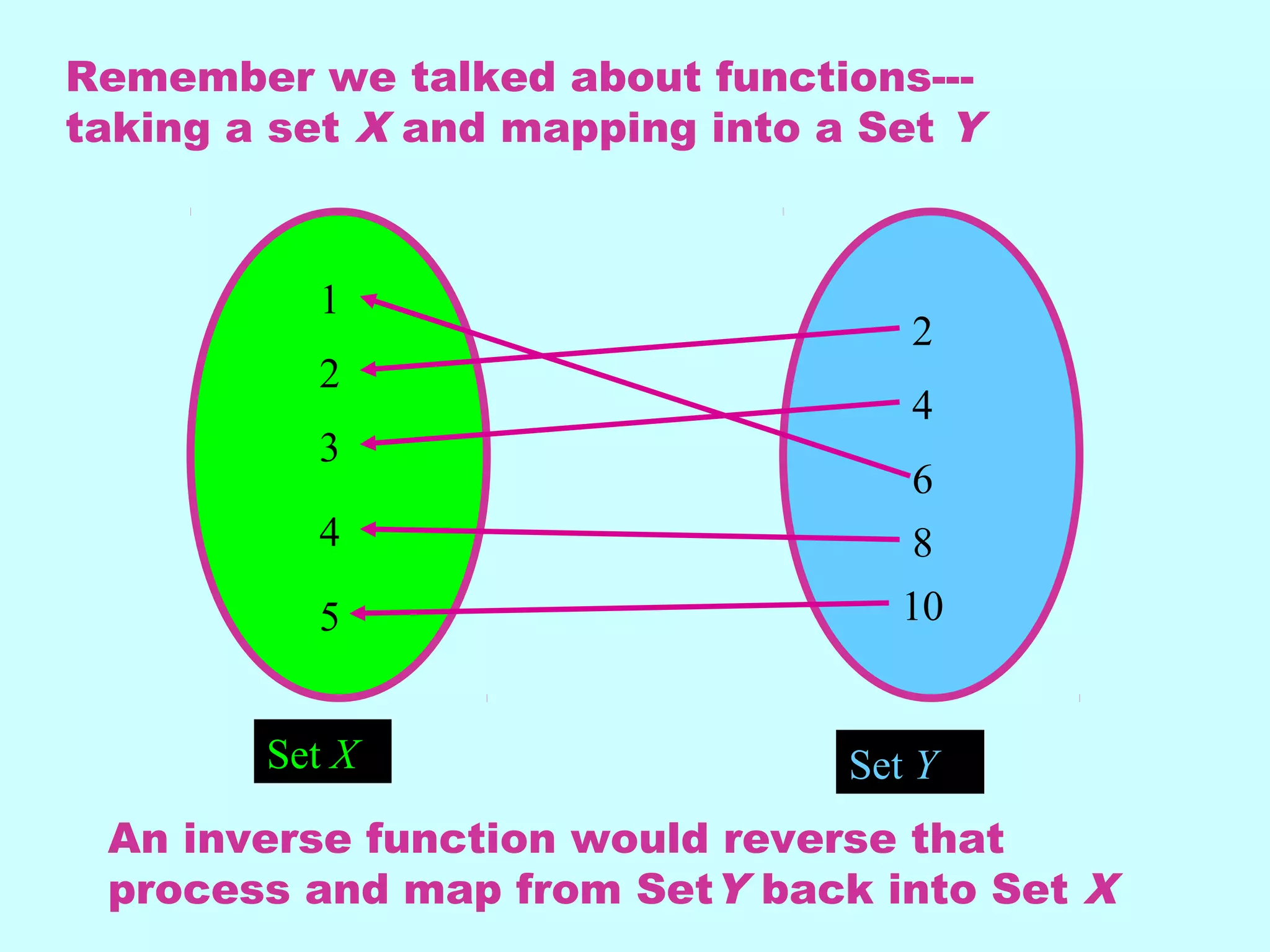
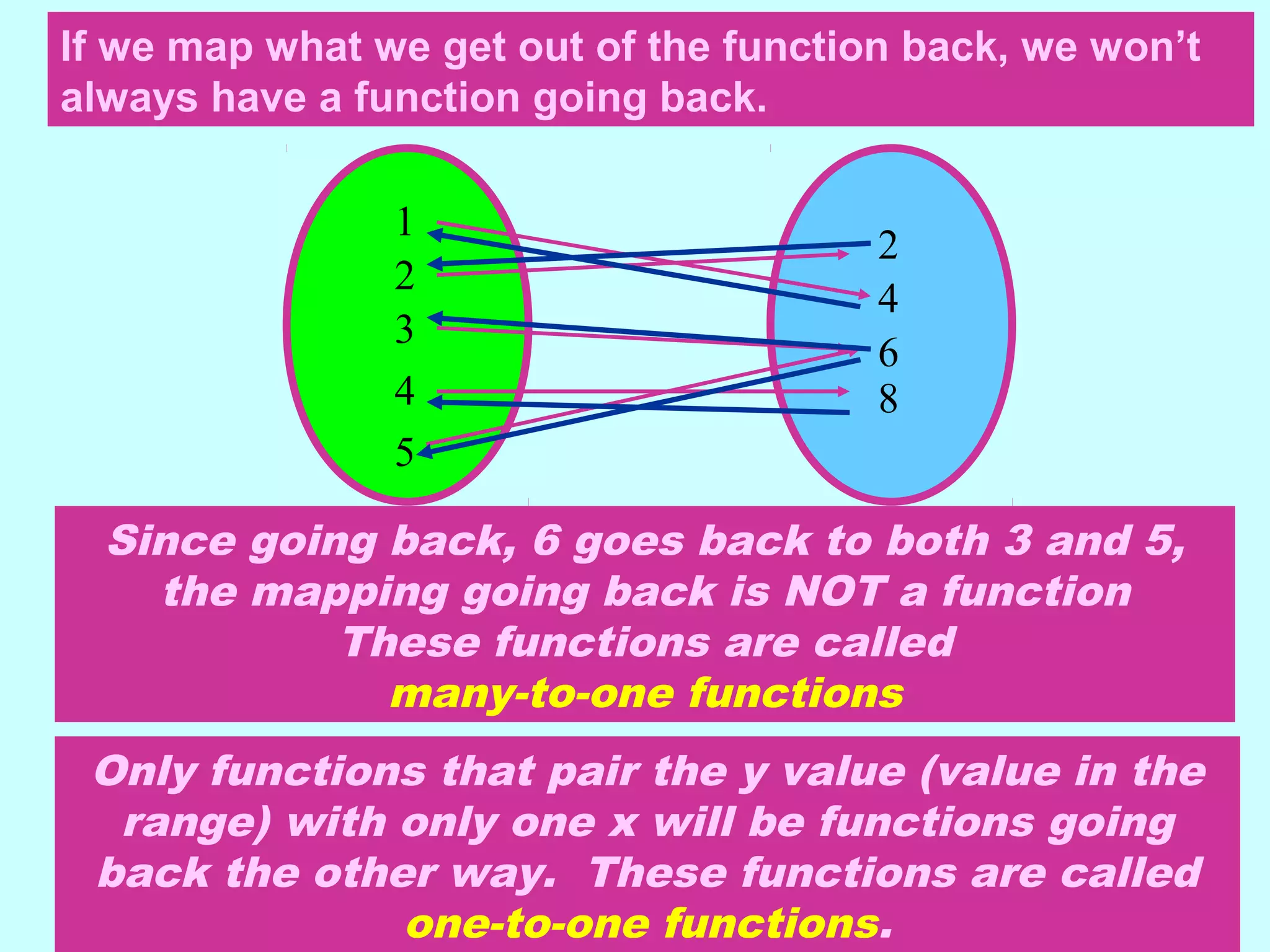
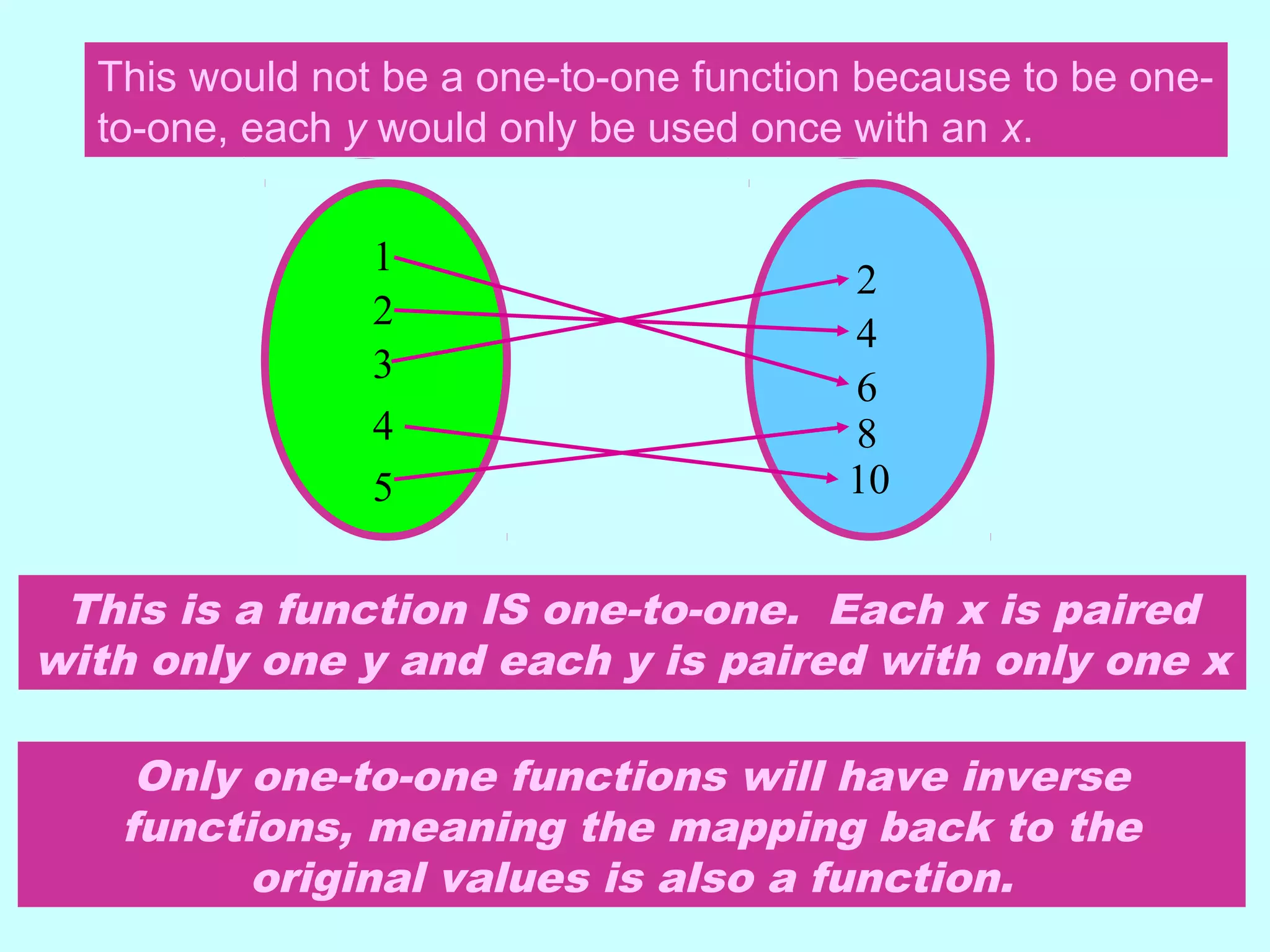
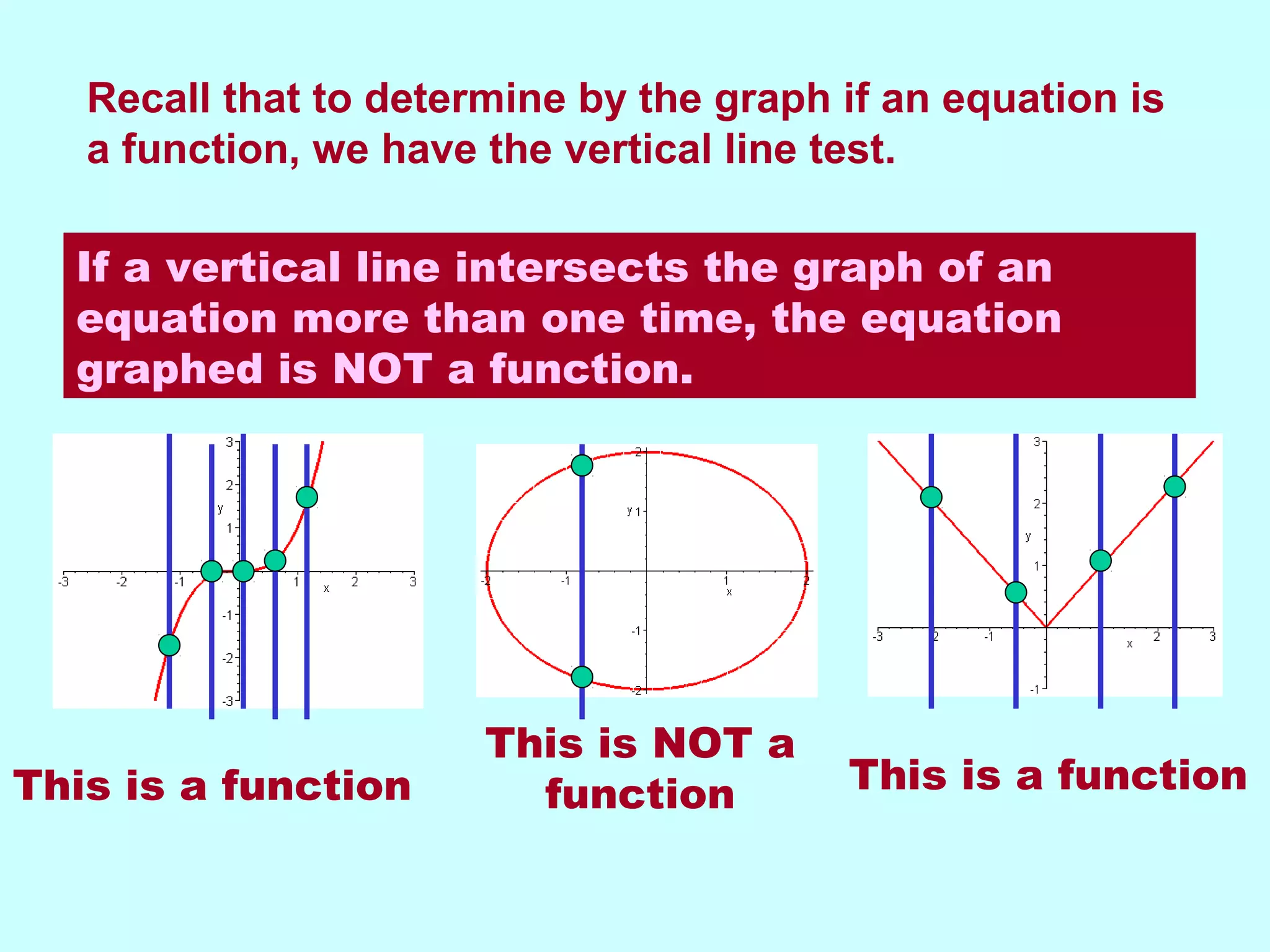
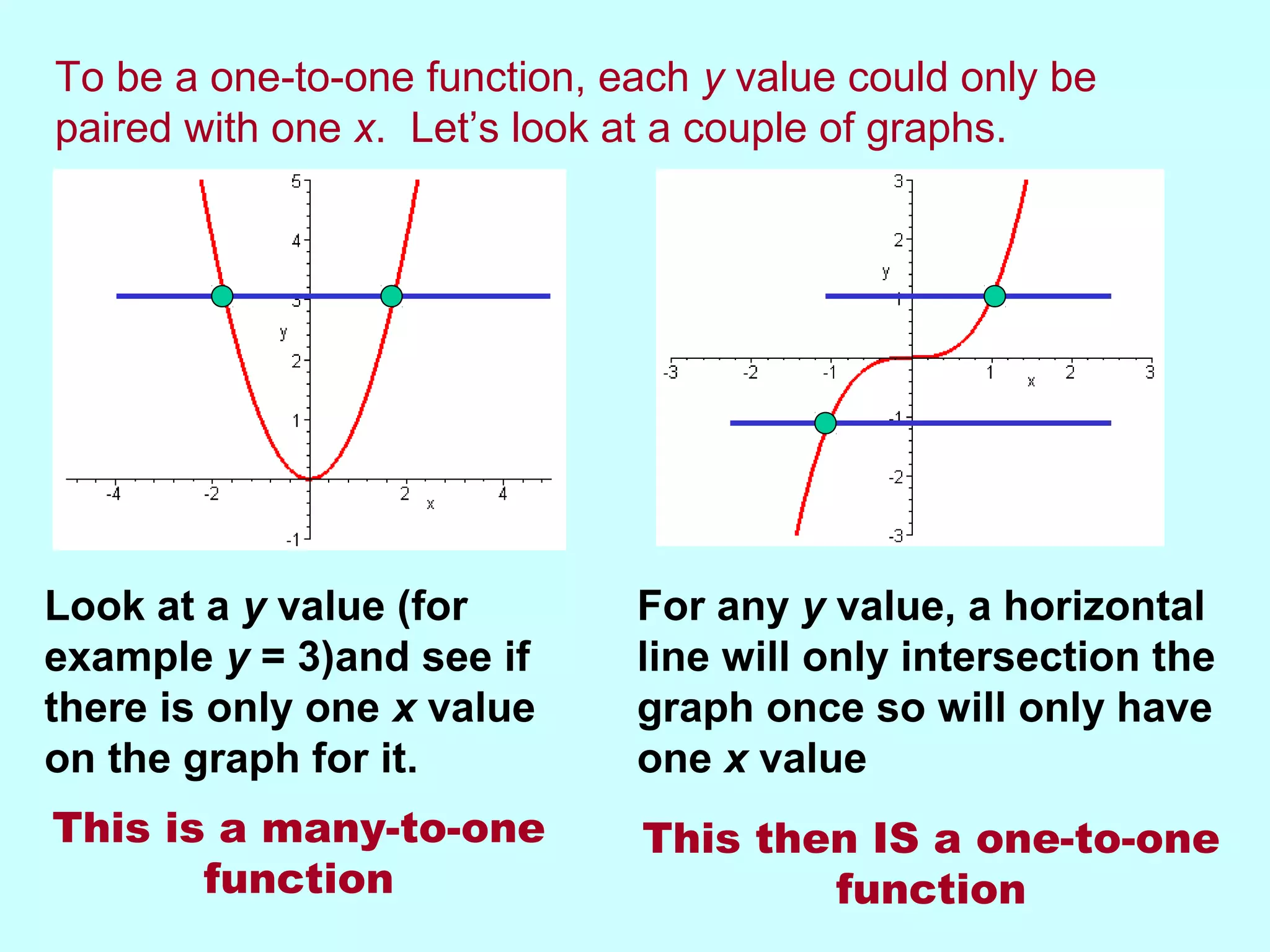
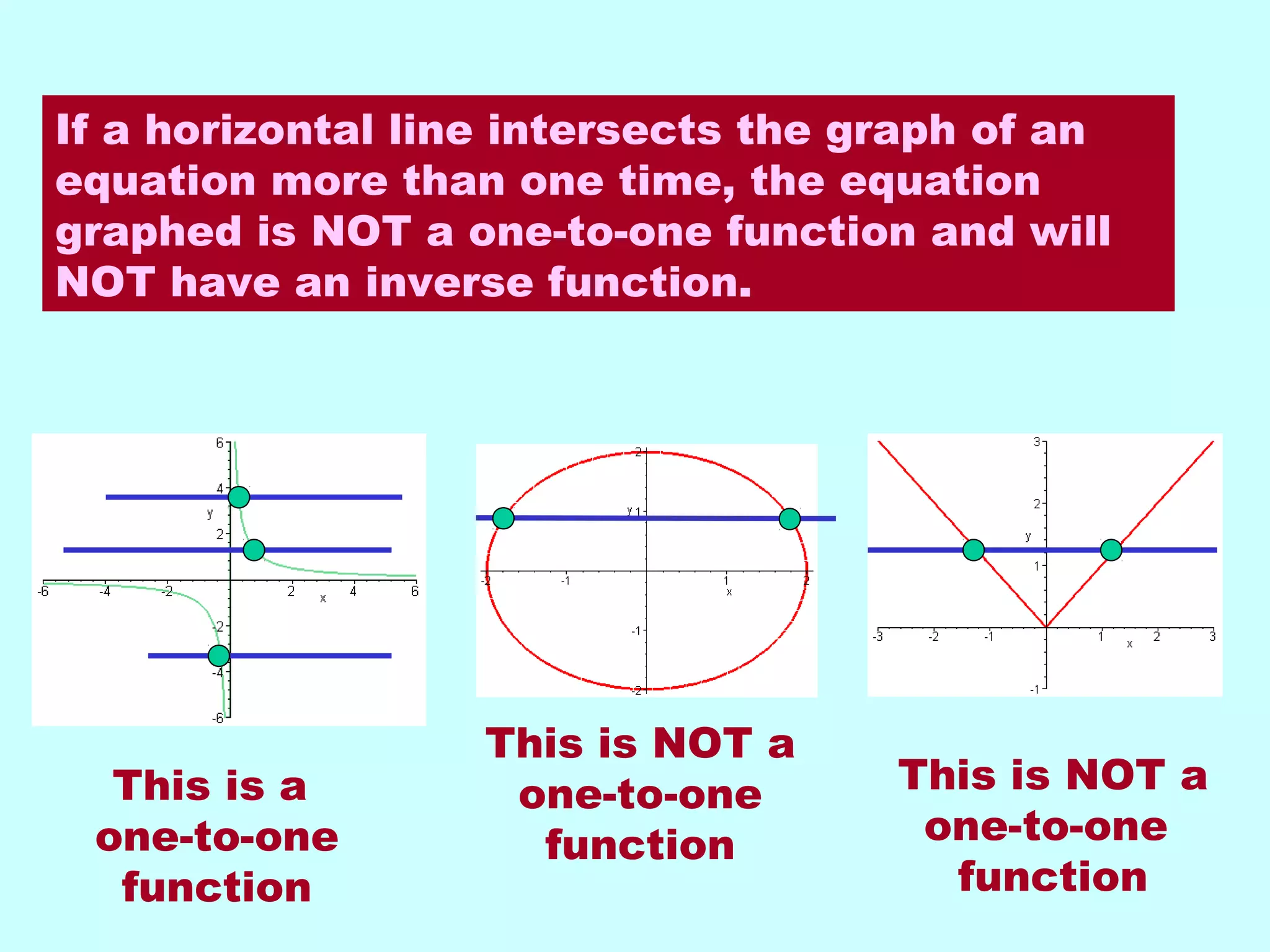
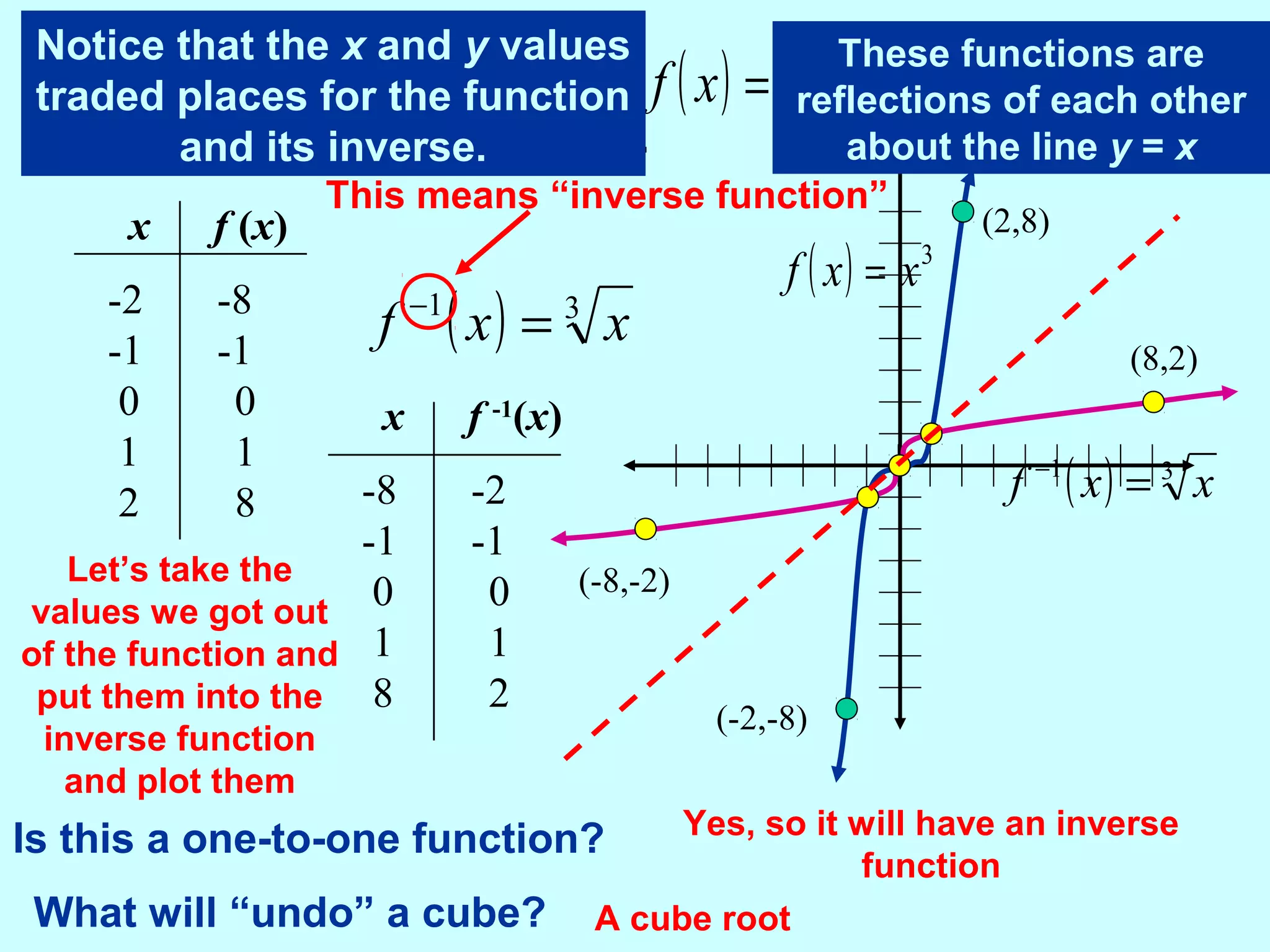
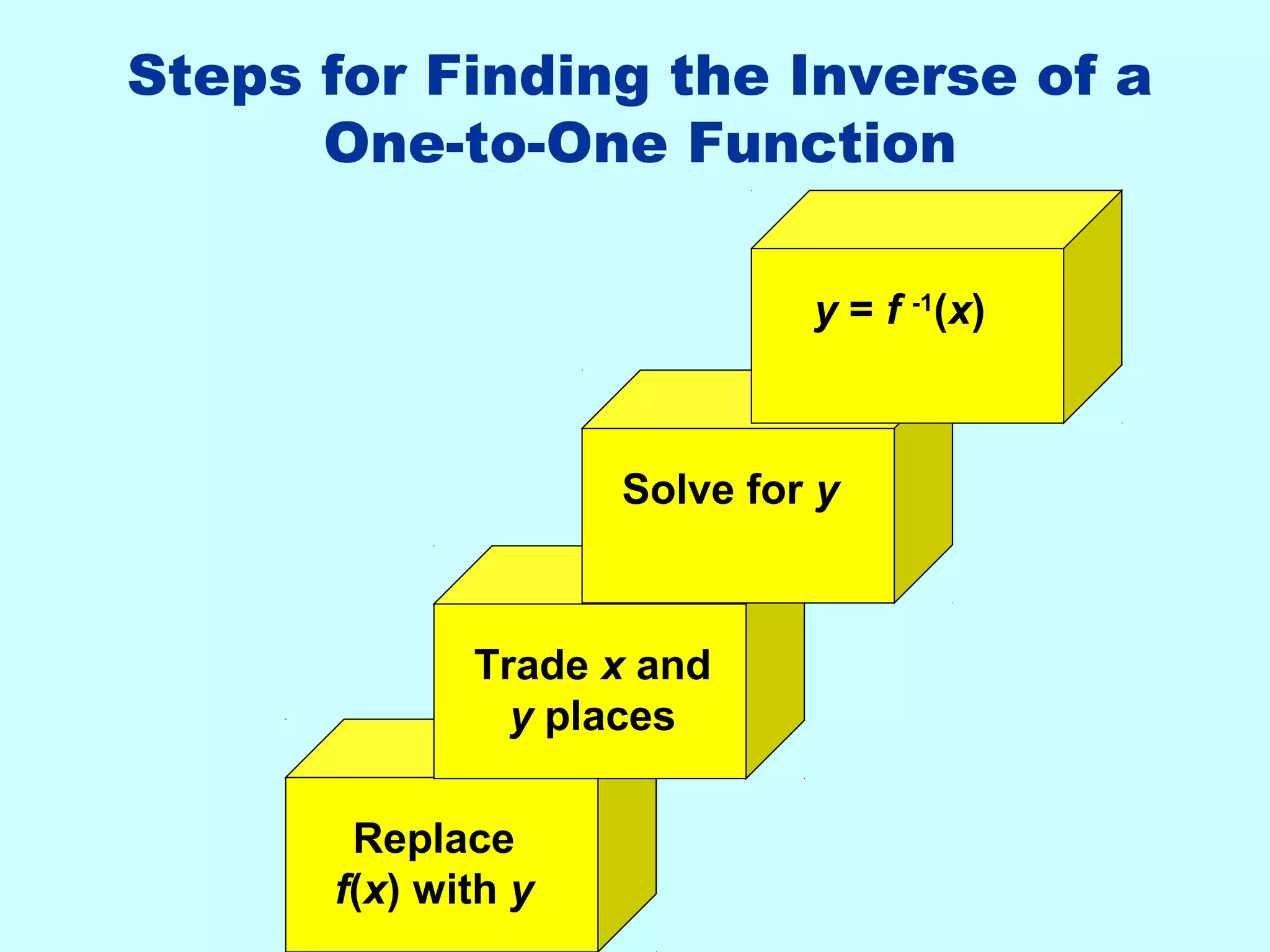
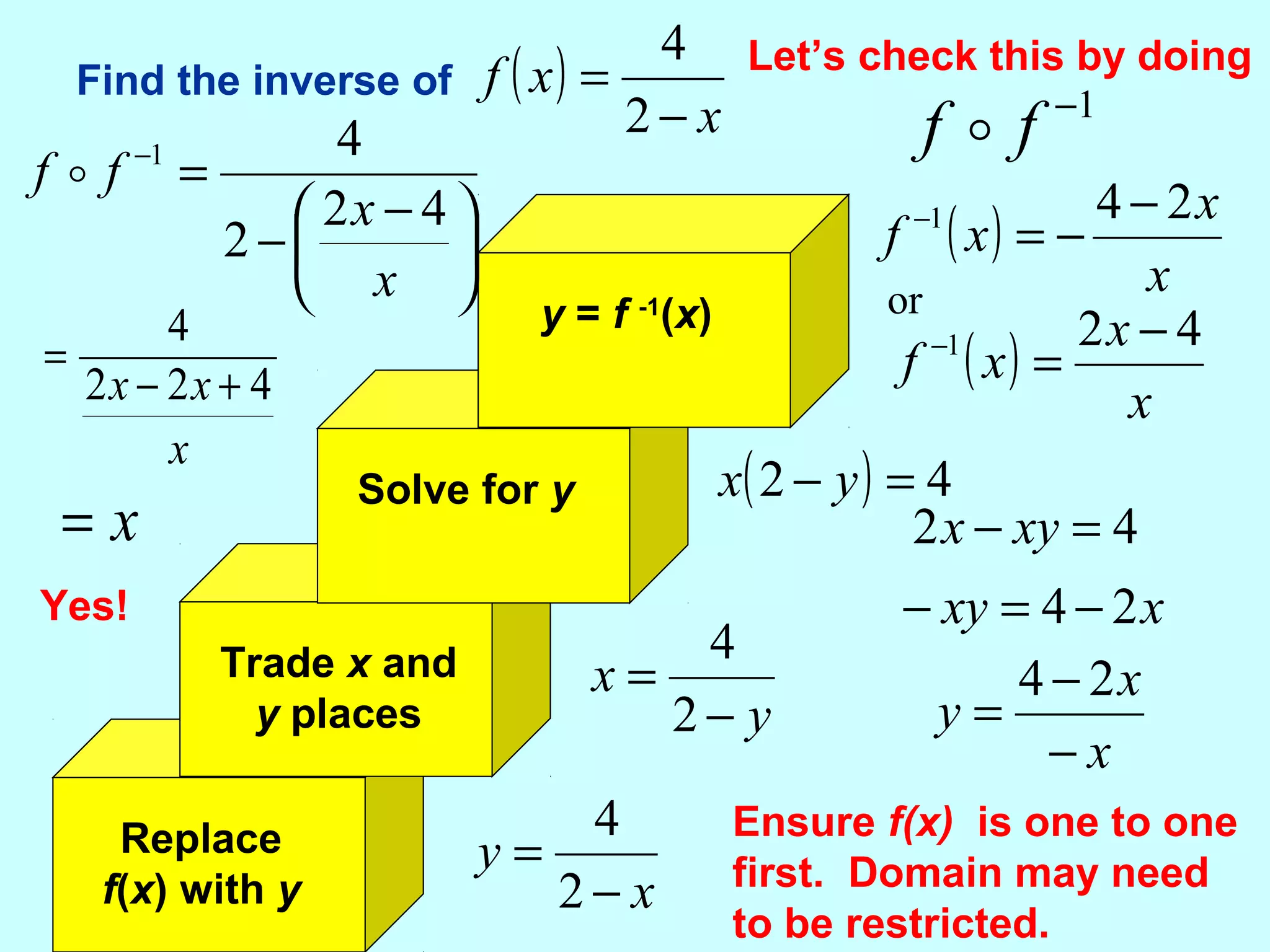
This document discusses inverse functions. It begins by explaining that an inverse function reverses the mapping of a regular function by mapping from the output set back to the input set. Only one-to-one functions, where each output is paired with exactly one input, will have inverse functions. The document provides examples of one-to-one and many-to-one functions through graphs and equations. It then outlines the steps to find the inverse of a function by replacing the function with y, swapping x and y, and solving for y. An example inverse function is worked through. The document emphasizes that the inverse undoes the original function when composed together.

1. INVERSE
FUNCTIONS
By
JUNREY P. FALCON

2. Set X Set Y
1
2
3
4
5
2
10
8
6
4
Remember we talked about functions---
taking a set X and mapping into a Set Y
An inverse function would reverse that
process and map from SetY back into Set X
1
2
3
4
5
2
10
8
6
4

3. 1
2
3
4
5
2
8
6
4
If we map what we get out of the function back, we won’t
always have a function going back.
Since going back, 6 goes back to both 3 and 5,
the mapping going back is NOT a function
These functions are called
many-to-one functions
Only functions that pair the y value (value in the
range) with only one x will be functions going
back the other way. These functions are called
one-to-one functions.

4. 1
2
3
4
5
2
10
8
6
4
This would not be a one-to-one function because to be one-
to-one, each y would only be used once with an x.
This is a function IS one-to-one. Each x is paired
with only one y and each y is paired with only one x
1
2
3
4
5
2
10
8
6
4
Only one-to-one functions will have inverse
functions, meaning the mapping back to the
original values is also a function.

5. Recall that to determine by the graph if an equation is
a function, we have the vertical line test.
If a vertical line intersects the graph of an
equation more than one time, the equation
graphed is NOT a function.
This is a function
This is NOT a
function This is a function

6. To be a one-to-one function, each y value could only be
paired with one x. Let’s look at a couple of graphs.
Look at a y value (for
example y = 3)and see if
there is only one x value
on the graph for it.
This is a many-to-one
function
For any y value, a horizontal
line will only intersection the
graph once so will only have
one x value
This then IS a one-to-one
function

7. If a horizontal line intersects the graph of an
equation more than one time, the equation
graphed is NOT a one-to-one function and will
NOT have an inverse function.
This is a
one-to-one
function
This is NOT a
one-to-one
function
This is NOT a
one-to-one
function

8. Let’s consider the function and compute
some values and graph them.
( ) 3
xxf =
x f (x)
-2 -8
-1 -1
0 0
1 1
2 8
Is this a one-to-one function? Yes, so it will have an inverse
function
What will “undo” a cube? A cube root
( ) 31
xxf =−
This means “inverse function”
x f -1
(x)
-8 -2
-1 -1
0 0
1 1
8 2
Let’s take the
values we got out
of the function and
put them into the
inverse function
and plot them
Notice that the x and y values
traded places for the function
and its inverse.
These functions are
reflections of each other
about the line y = x
( ) 3
xxf =
( ) 31
xxf =−
(2,8)
(8,2)
(-8,-2)
(-2,-8)

9. So geometrically if a function and its inverse are
graphed, they are reflections about the line y = x and the
x and y values have traded places. The domain of the
function is the range of the inverse. The range of the
function is the domain of the inverse. Also if we start
with an x and put it in the function and put the result in
the inverse function, we are back where we started from.
Given two functions, we can then tell if they are inverses
of each other if we plug one into the other and it
“undoes” the function. Remember subbing one function
in the other was the composition function.
( )( ) xxgfgf == ( )( ) xxfgfg ==
So if f and g are inverse functions, their composition
would simply give x back. For inverse functions then:

10. Verify that the functions f and g are inverses of each other.
( ) ( ) ( ) 2;2,2
2
+=≥−= xxgxxxf
If we graph (x - 2)2
it is a parabola shifted right 2.
Is this a one-to-one function?
This would not be one-to-one
but they restricted the domain
and are only taking the
function where x is greater
than or equal to 2 so we will
have a one-to-one function.

11. Verify that the functions f and g are inverses of each other.
( ) ( ) ( ) 2;2,2
2
+=≥−= xxgxxxf
( ) xxxgf ==−+=
22
22
( ) xxxfg =+−=+−= 2222
2

Since both of these = x, if you start with x and apply the
functions they “undo” each other and are inverses.

12. Steps for Finding the Inverse of a
One-to-One Function
Replace
f(x) with y
Trade x and
y places
Solve for y
y = f -1
(x)

13. Find the inverse of
Replace
f(x) with y
Trade x and
y places
Solve for y
y = f -1
(x)
( )
x
xf
−
=
2
4
x
y
−
=
2
4
y
x
−
=
2
4
( ) 42 =− yx
42 =− xyx
xxy 24 −=−
x
x
y
−
−
=
24
( )
x
x
xf
241 −
−=−
Let’s check this by doing
1−
ff 





 −
−
=−
x
x
ff
42
2
41

x
xx 422
4
+−
=
x=
Yes!
( )
x
x
xf
421 −
=−
or
Ensure f(x) is one to one
first. Domain may need
to be restricted.

14. Acknowledgement
I wish to thank Shawna Haider from Salt Lake Community College, Utah
USA for her hard work in creating this PowerPoint.
www.slcc.edu
Shawna has kindly given permission for this resource to be downloaded
from www.mathxtc.com and for it to be modified to suit the Western
Australian Mathematics Curriculum.
Stephen Corcoran
Head of Mathematics
St Stephen’s School – Carramar
www.ststephens.wa.edu.au