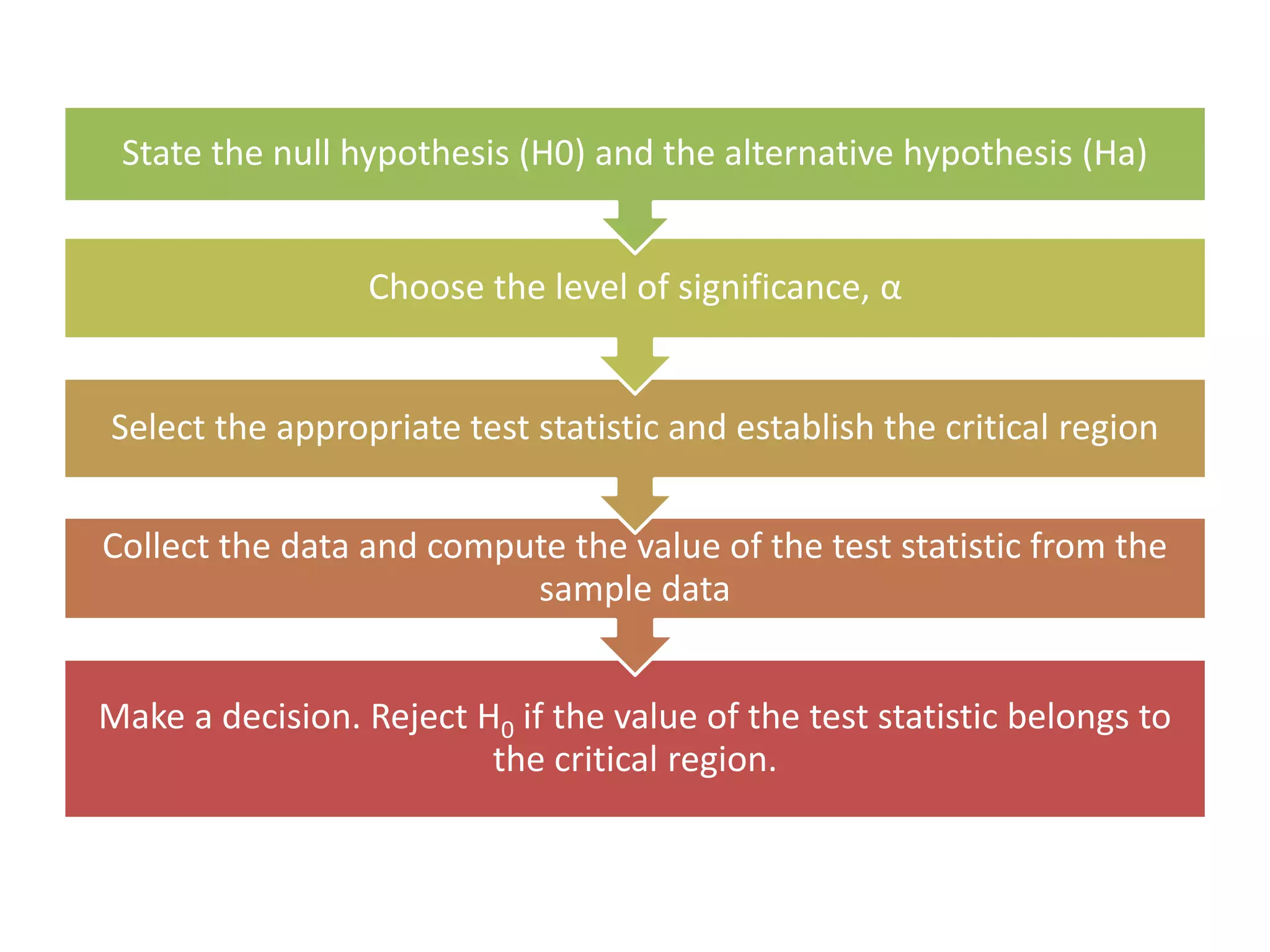
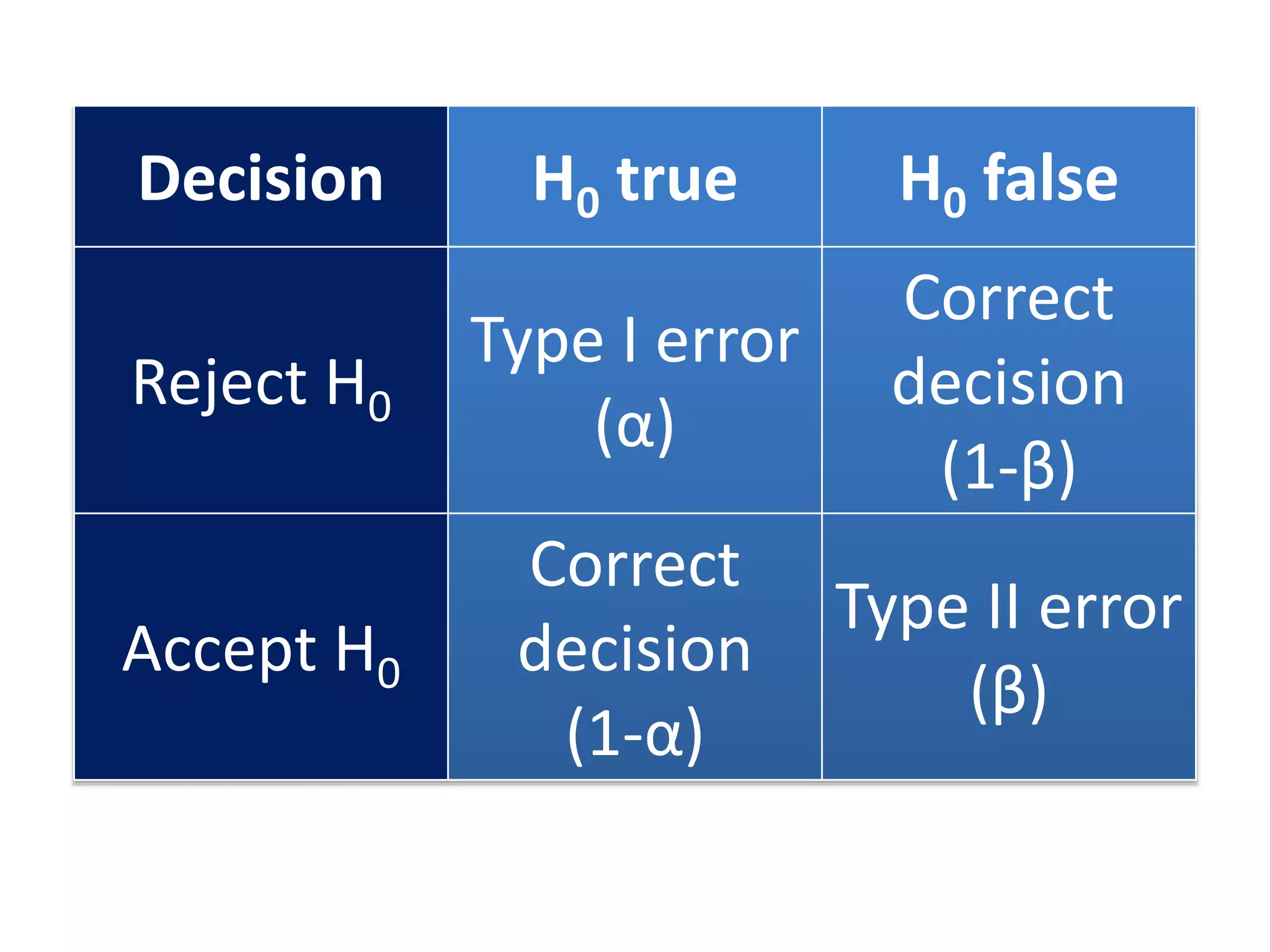
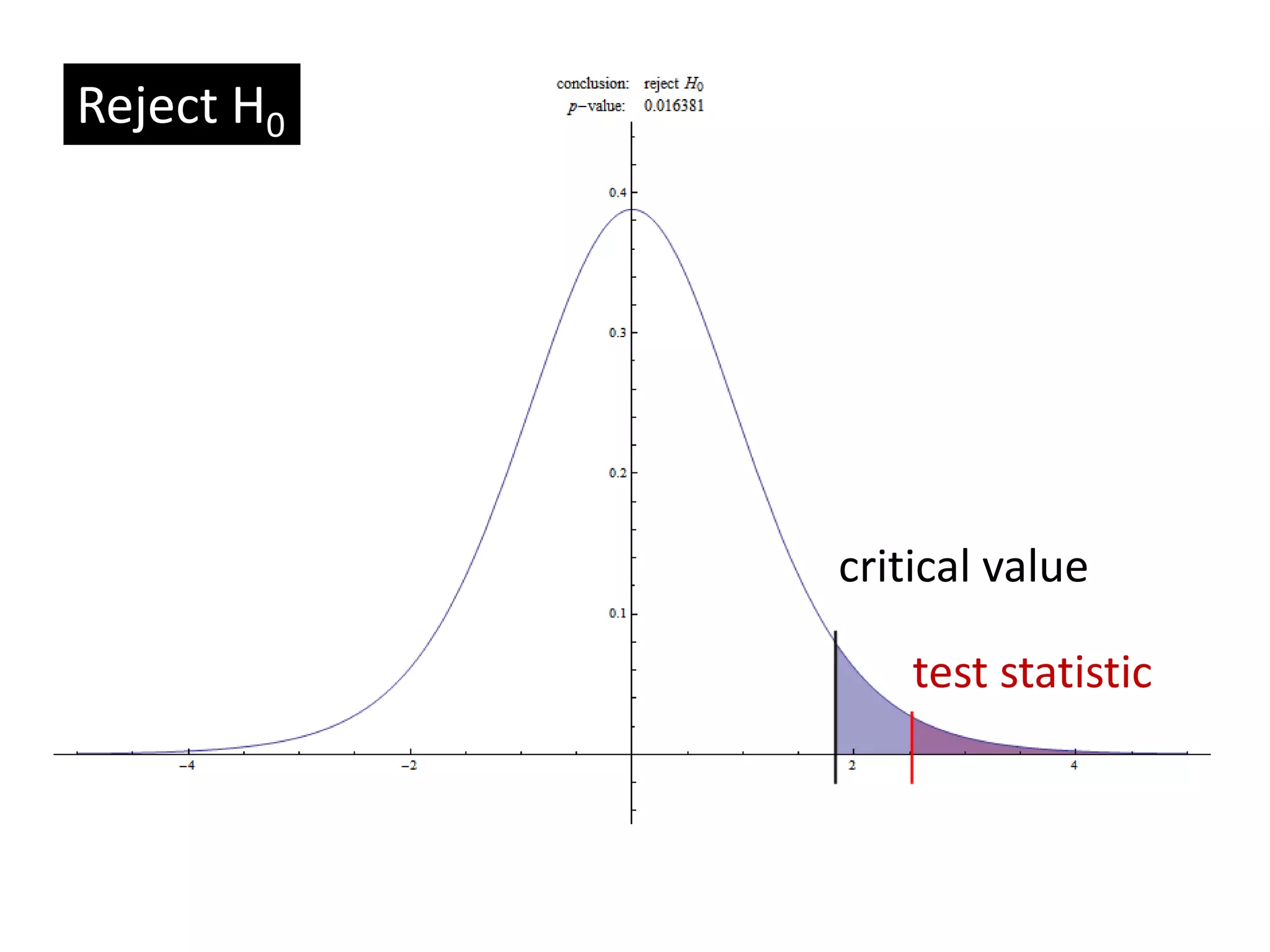
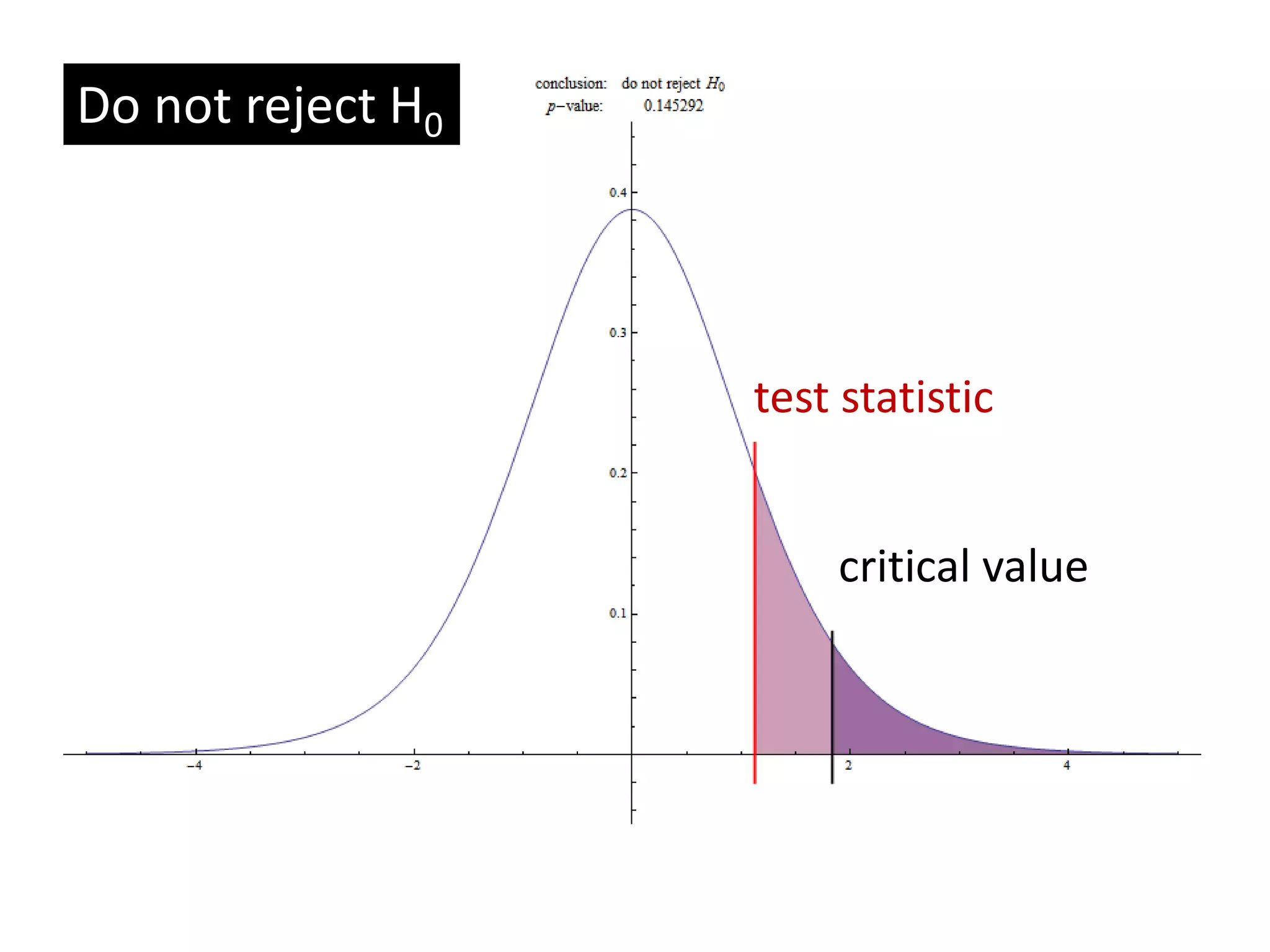
This document discusses hypothesis testing and the key concepts involved, including: - The difference between the null and alternative hypotheses, with the null hypothesis representing the hypothesis being tested. - Whether tests are one-tailed or two-tailed depending on if the alternative hypothesis specifies a directional difference. - Type I and Type II errors, with Type I errors occurring when the null hypothesis is incorrectly rejected and Type II errors occurring when it is incorrectly accepted.

1. HYPOTHESIS TESTING
Normal Distribution and Hypothesis Testing

2. Hypothesis Testing
• A hypothesis is a conjecture or assertion
about a parameter
• Null v. Alternative hypothesis
– Proof by contradiction
– Null hypothesis is the hypothesis being tested
– Alternative hypothesis is the operational
statement of the experiment that is believed to be
true

3. Null Hypothesis
• The hypothesis stating that the manipulation has no
effect and that there will be no difference between
the two groups
– H0: μ1 - μ2 = 0
– H0: μ1 = μ2

4. Alternative Hypothesis
• The hypothesis stating that the manipulation has an
effect and that there will be difference between the
two groups
– HA: μ1 < μ2 (one-tailed)
– HA: μ1 > μ2 (one-tailed)
– HA: μ1 ≠ μ2 (two-tailed)

5. One-tailed test
• Alternative hypothesis specifies a one-directional
difference for parameter
– H0: μ = 10 v. Ha: μ < 10
– H0: μ = 10 v. Ha: μ > 10
– H0: μ1 - μ2 = 0 v. Ha: μ1 - μ2 > 0
– H0: μ1 - μ2 = 0 v. Ha: μ1 - μ2 < 0

6. Two-tailed test
• Alternative hypothesis does not specify a directional
difference for the parameter of interest
– H0: μ = 10 v. Ha: μ ≠ 10
– H0: μ1 - μ2 = 0 v. Ha: μ1 - μ2 ≠ 0

7. Example
Title: The NSAT Scores and Academic Achievement of the
Students in Private School and Public Schools.
H0: There is no significant relationship between the NSAT
performance and the academic achievement among the
four learning areas of private schools, public schools and
combination of private and public schools
Ha: There is a significant relationship between the NSAT
performance and the academic achievement among the
four learning areas of private schools, public schools and
combination of private and public schools

8. Critical Region
• Also known as the “rejection region”
• Critical region contains values of the test
statistic for which the null hypothesis will be
rejected
• Acceptance and rejection regions are
separated by the critical value, Z.

9. Type I error
• Error made by rejecting the null hypothesis
when it is true.
• False positive
• Denoted by the level of significance, α
• Level of significance suggests the highest
probability of committing a type I error

10. Type II error
• Error made by not rejecting (accepting) the
null hypothesis when it is false.
• False negative
• Probability denoted by β

11. Decision H0 true H0 false
Reject H0
Type I error
(α)
Correct
decision
(1-β)
Accept H0
Correct
decision
(1-α)
Type II error
(β)

12. Notes on errors
• Type I (α) and type II errors (β) are related. A
decrease in the probability of one, increases
the probability in the other.
• As α increases, the size of the critical region
also increases
• Consequently, if H0 is rejected at a low α, H0
will also be rejected at a higher α.

13. critical value
test statistic
Reject H0

14. critical value
test statistic
Do not reject H0

15. Make a decision. Reject H0 if the value of the test statistic belongs to
the critical region.
Collect the data and compute the value of the test statistic from the
sample data
Select the appropriate test statistic and establish the critical region
Choose the level of significance, α
State the null hypothesis (H0) and the alternative hypothesis (Ha)

16. Independent-Groups and
Correlated-Groups T Tests
Independent Group t Test Correlated Group t Test
What it is A parametric test for a
two-group between-
participants design
A parametric test for a
two-group within-
participants or matched
participants design
What it does Compares performance of
the two groups to
determine whether they
represent the same
population or different
populations
Analyzes whether each
individual performed in a
similar or different manner
across conditions
Assumptions Interval-ratio data
Bell-shaped distribution
Independent observations
Homogeneity of variance
Interval-ratio data
Bell-shaped distribution
Dependent observations
Homogeneity of variance