Downloaded 57 times
Uploaded byAditya Abeysinghe Presentations
Mechanics 3
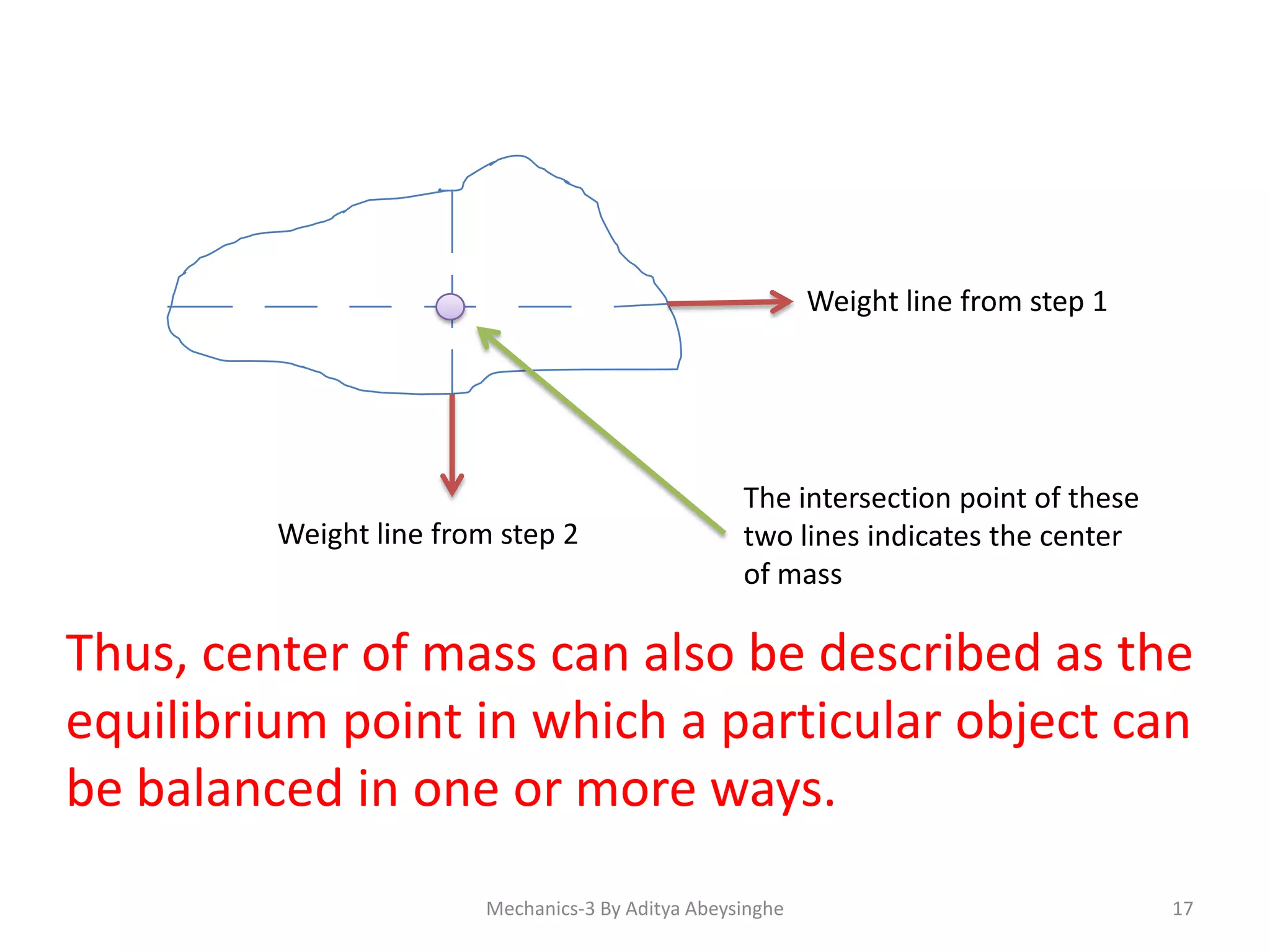
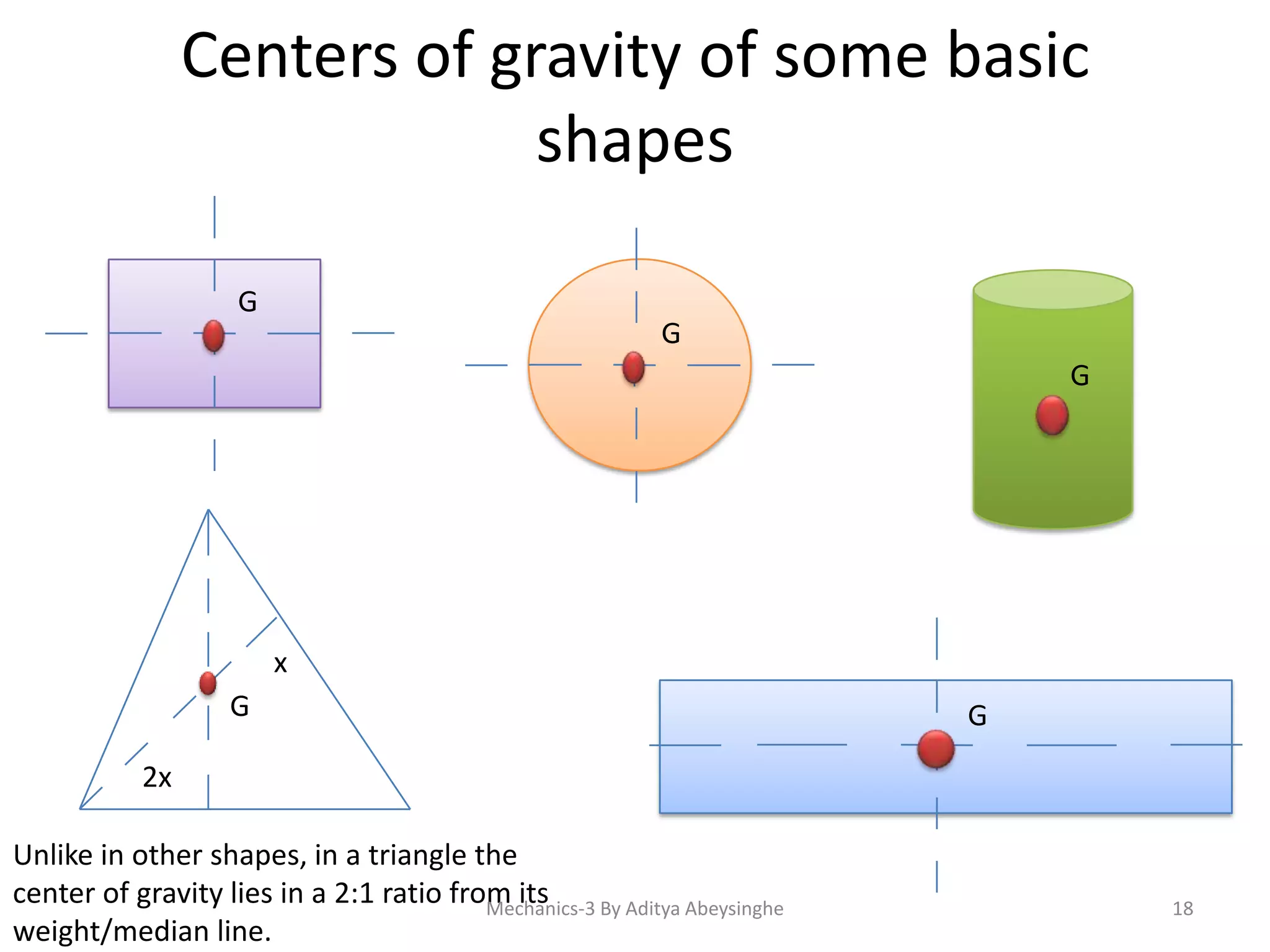
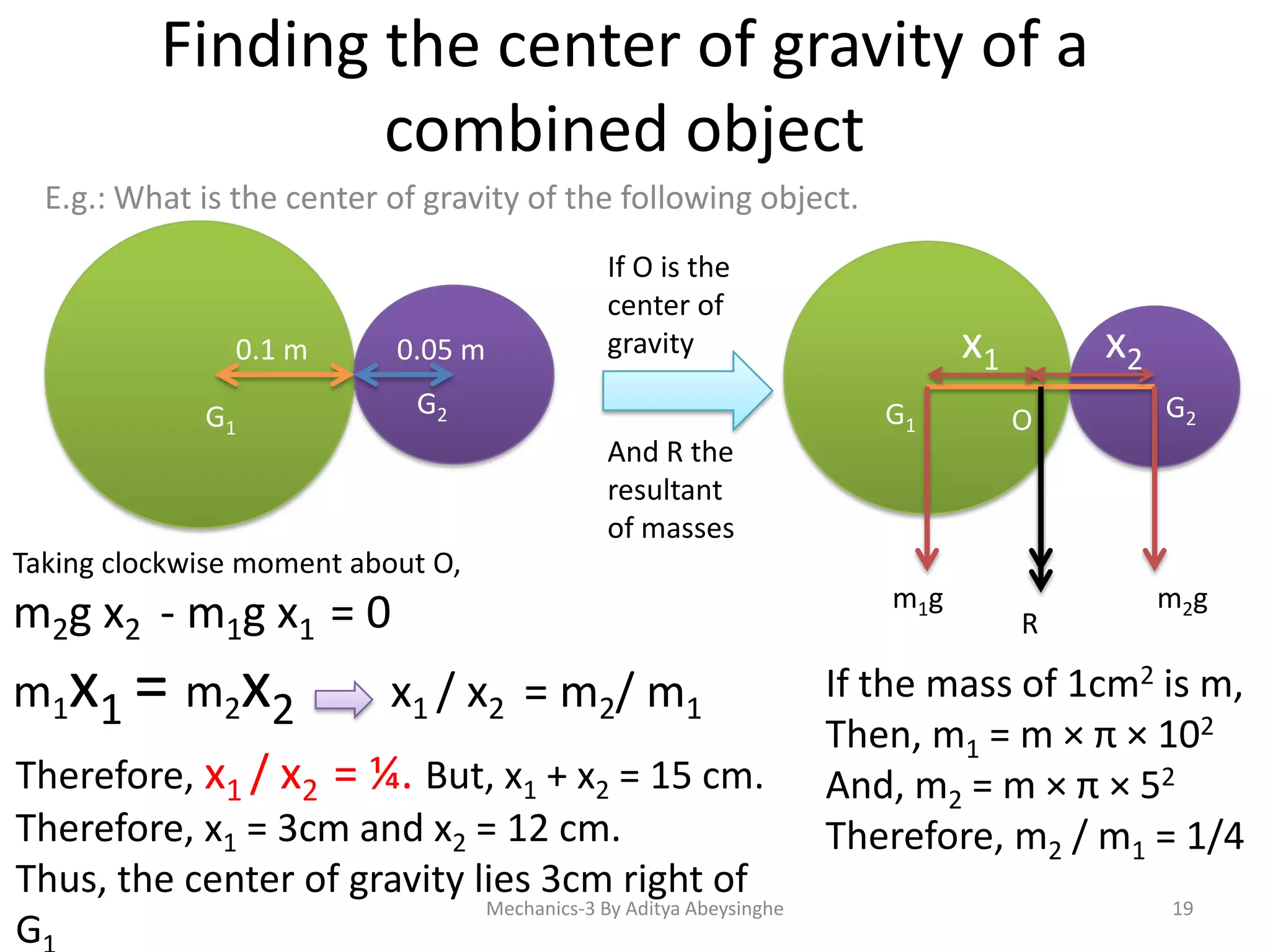
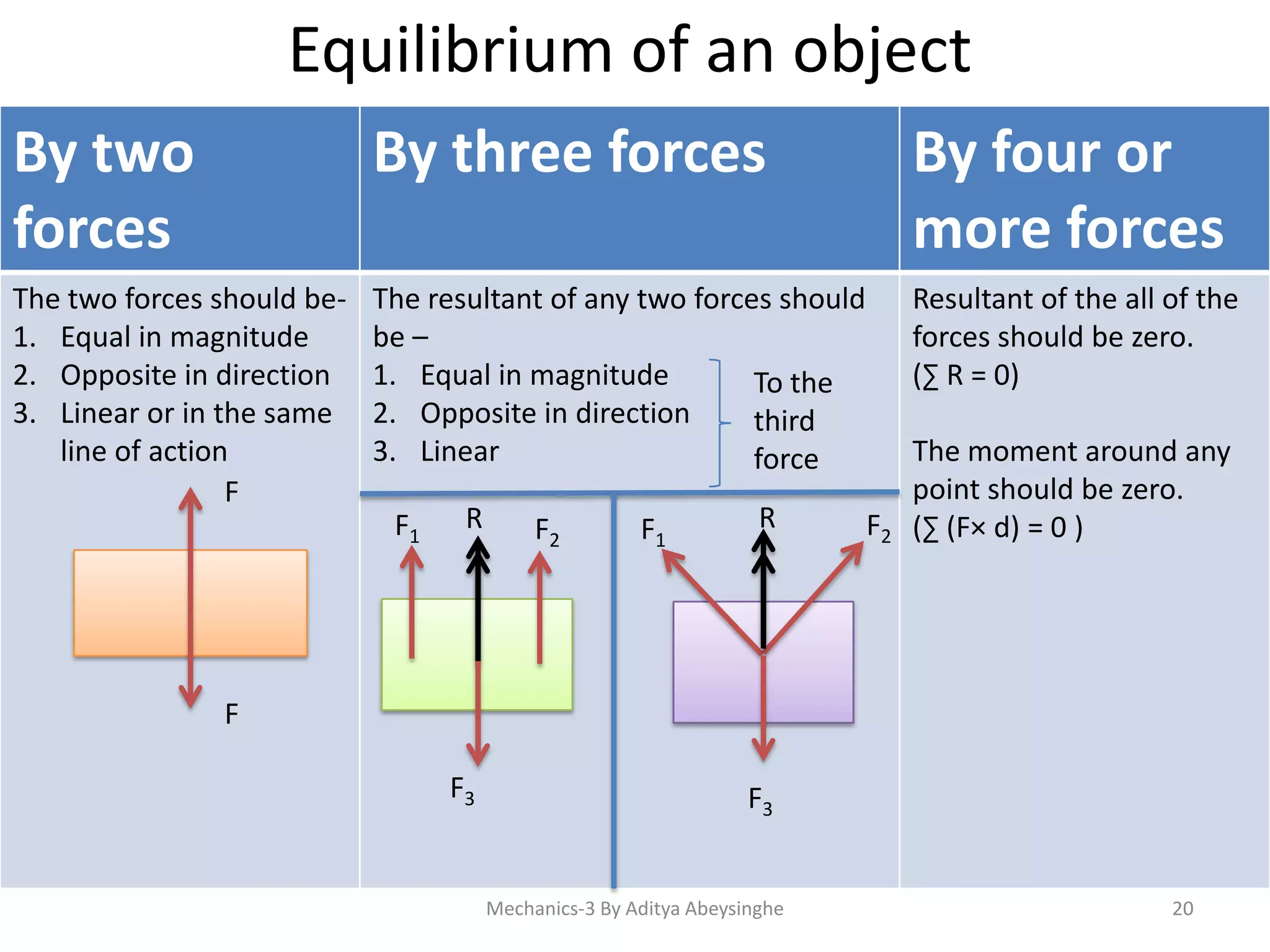
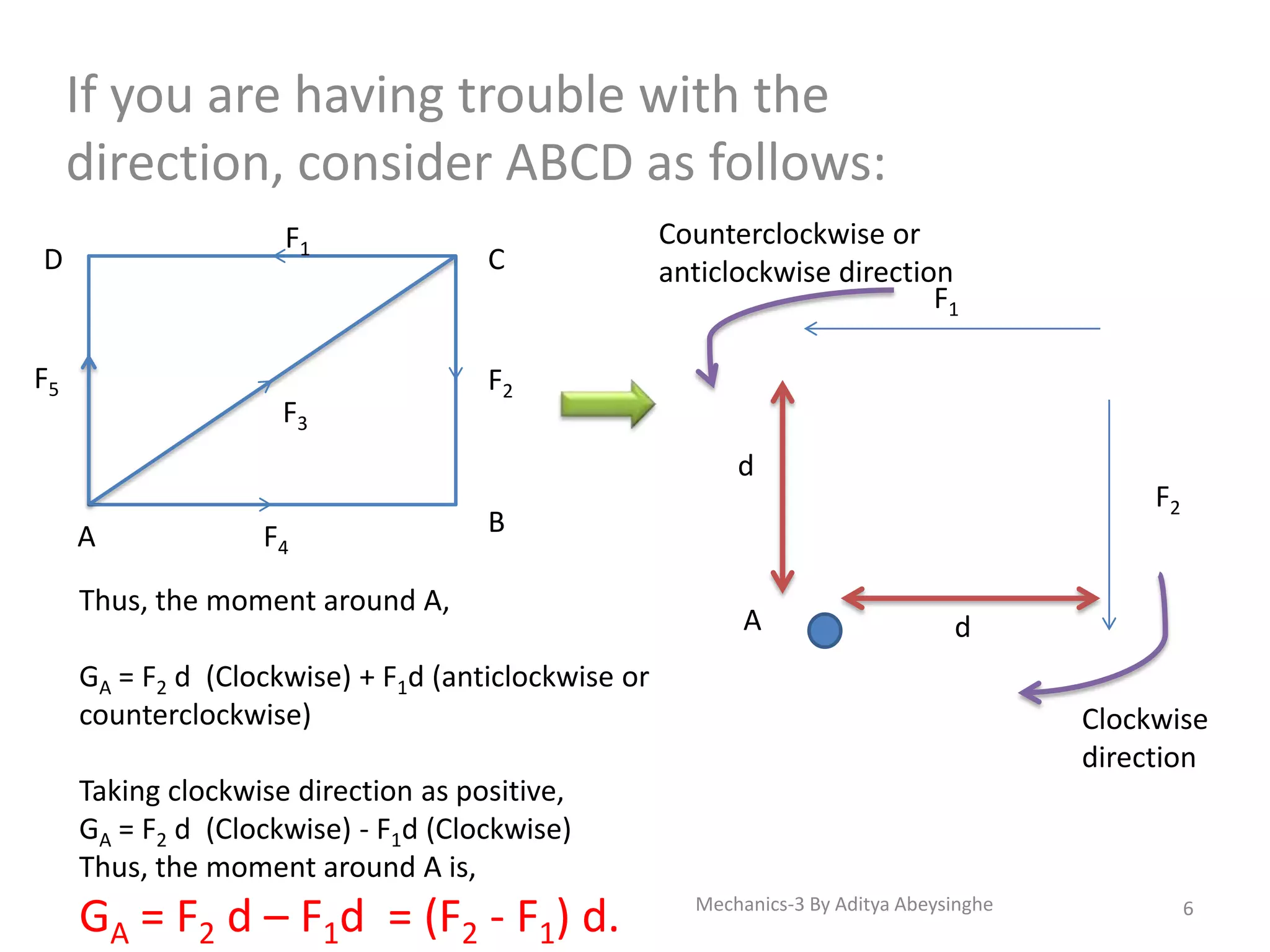
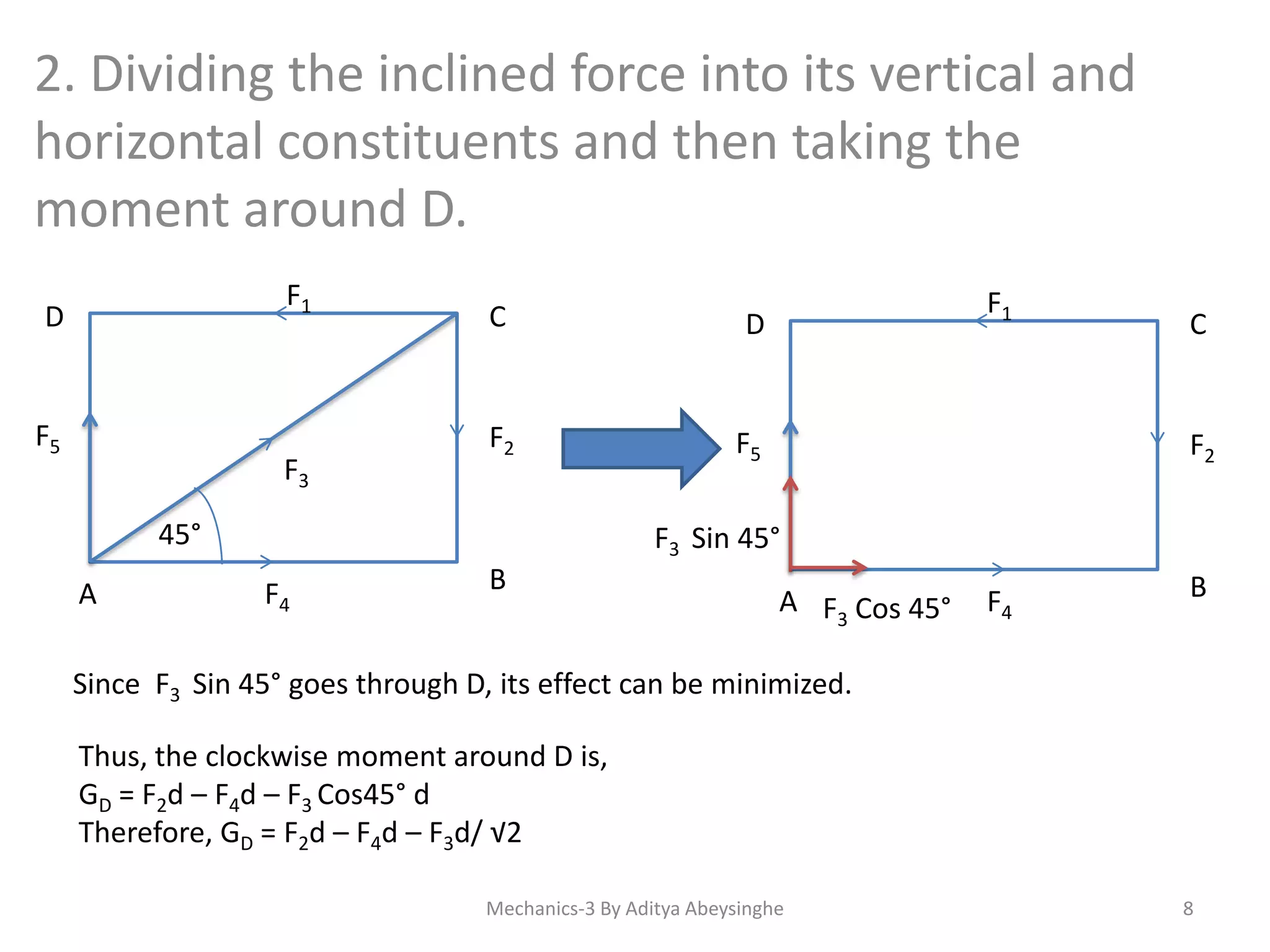
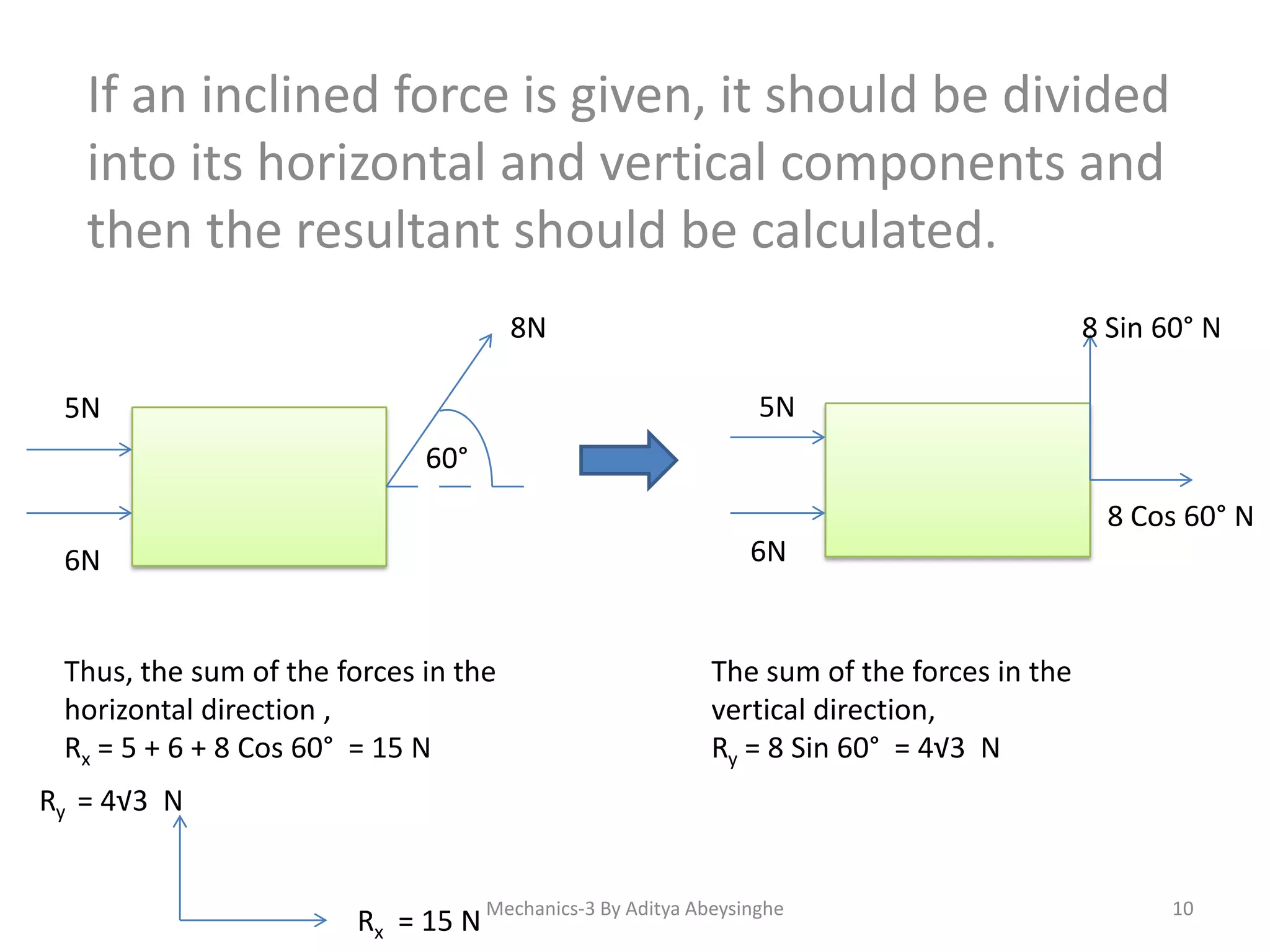
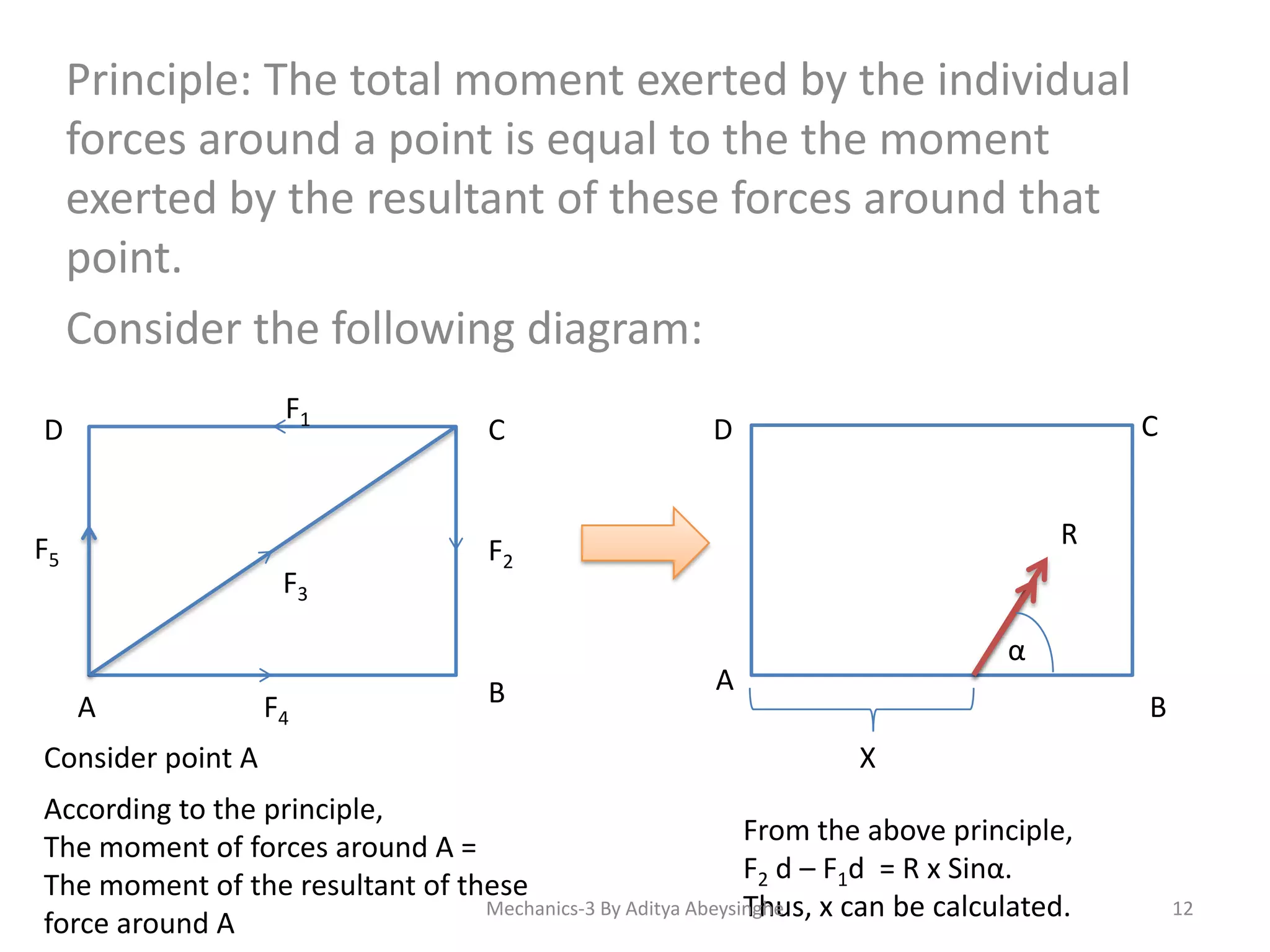
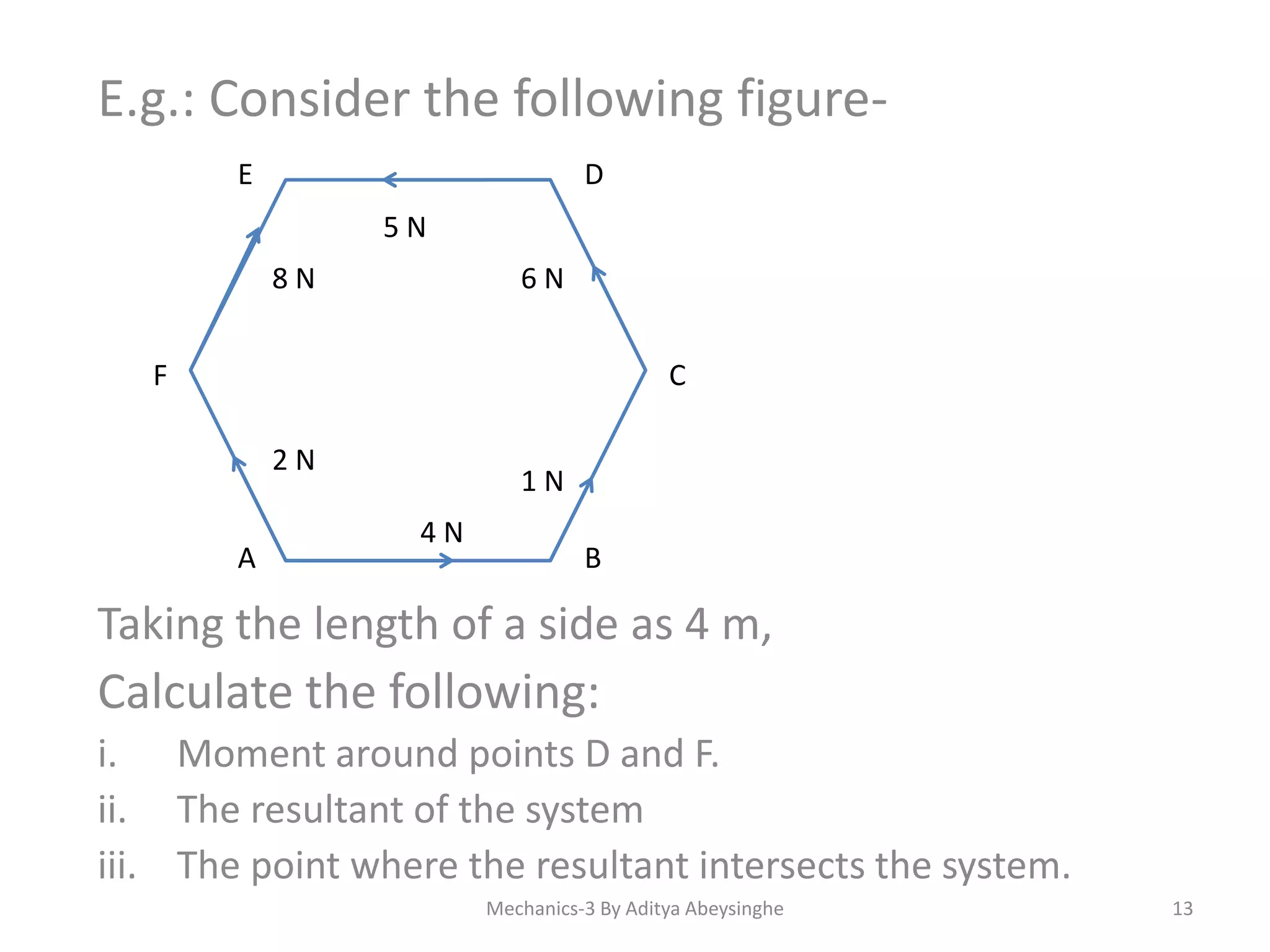
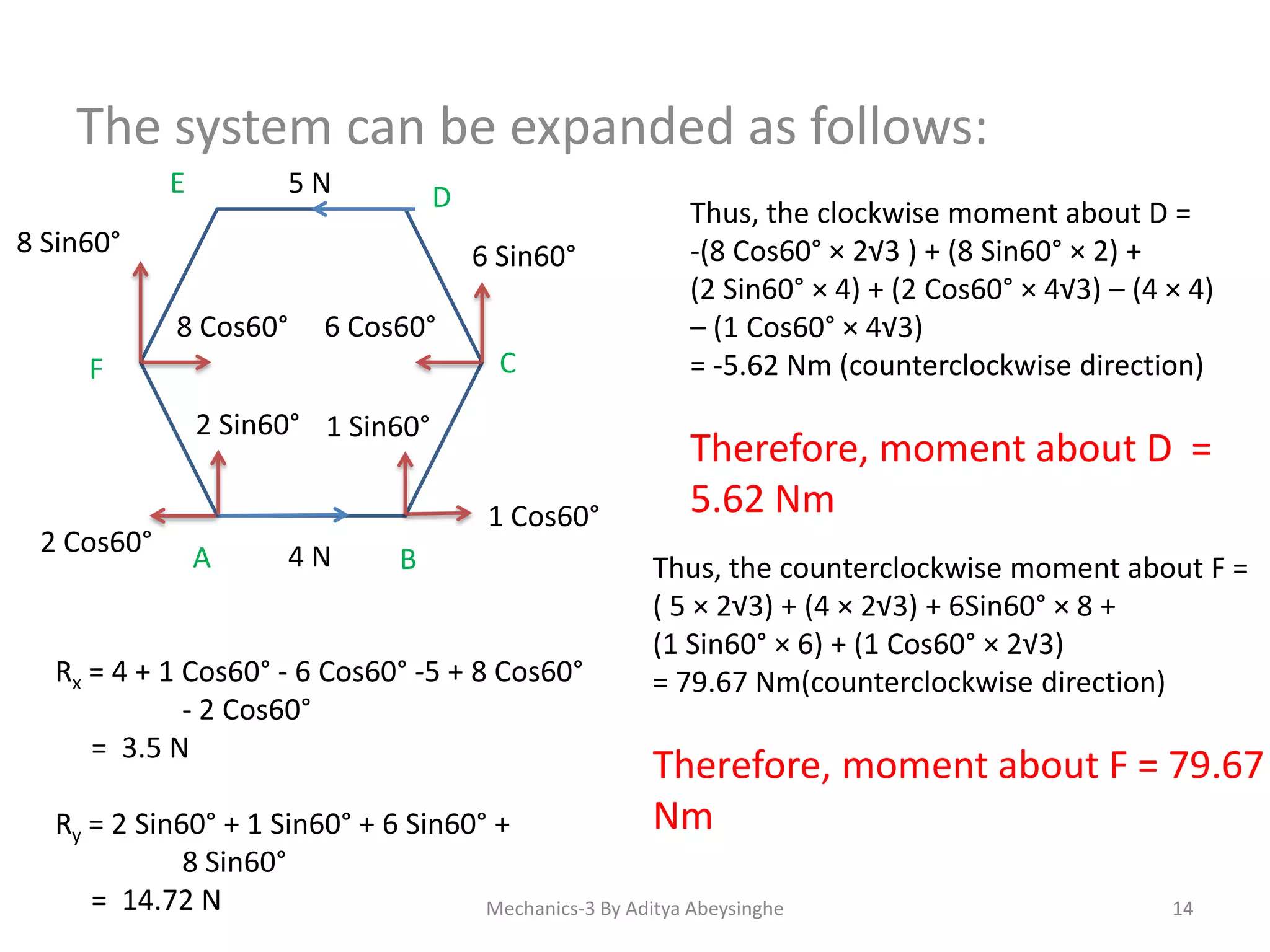
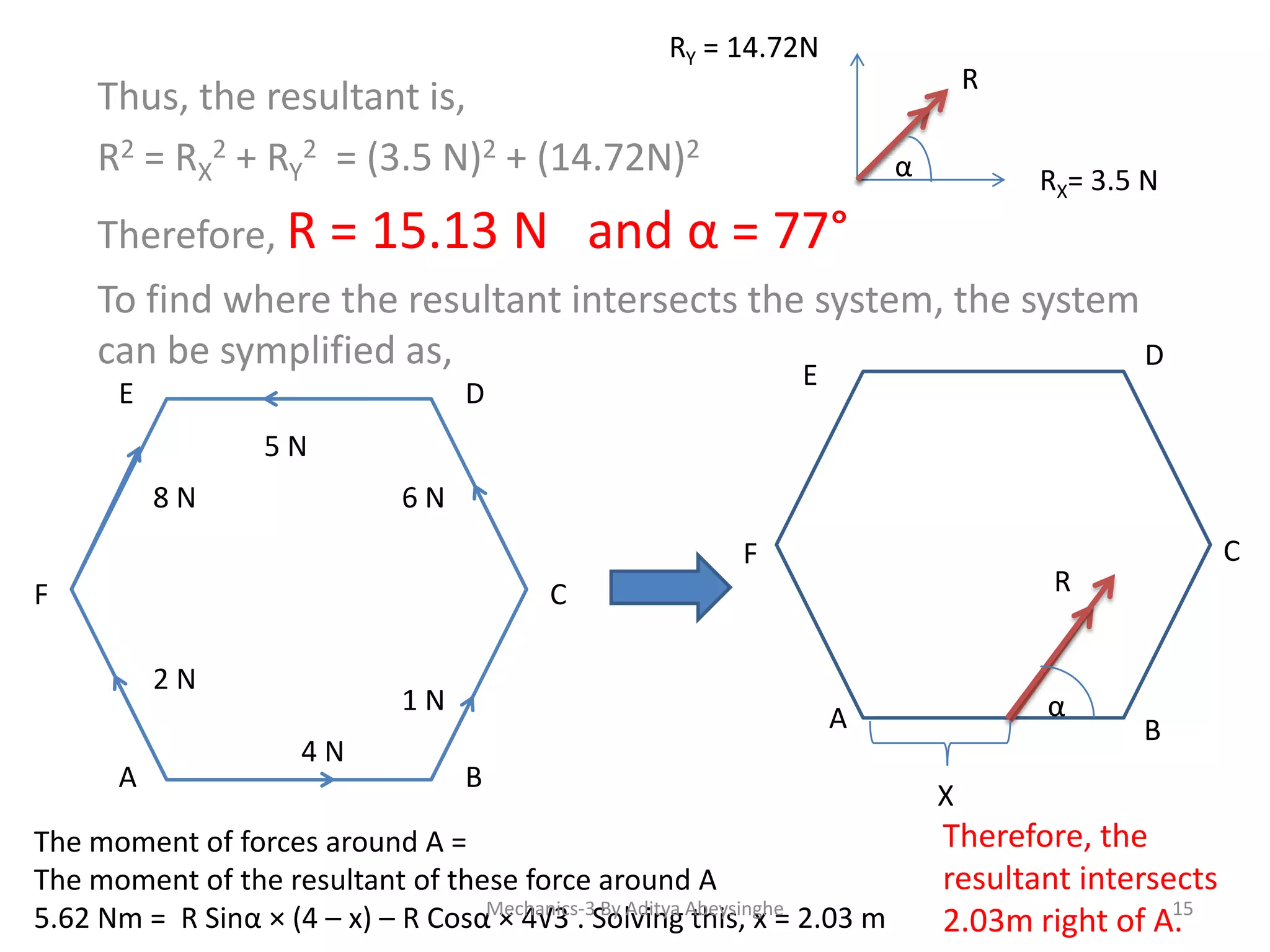
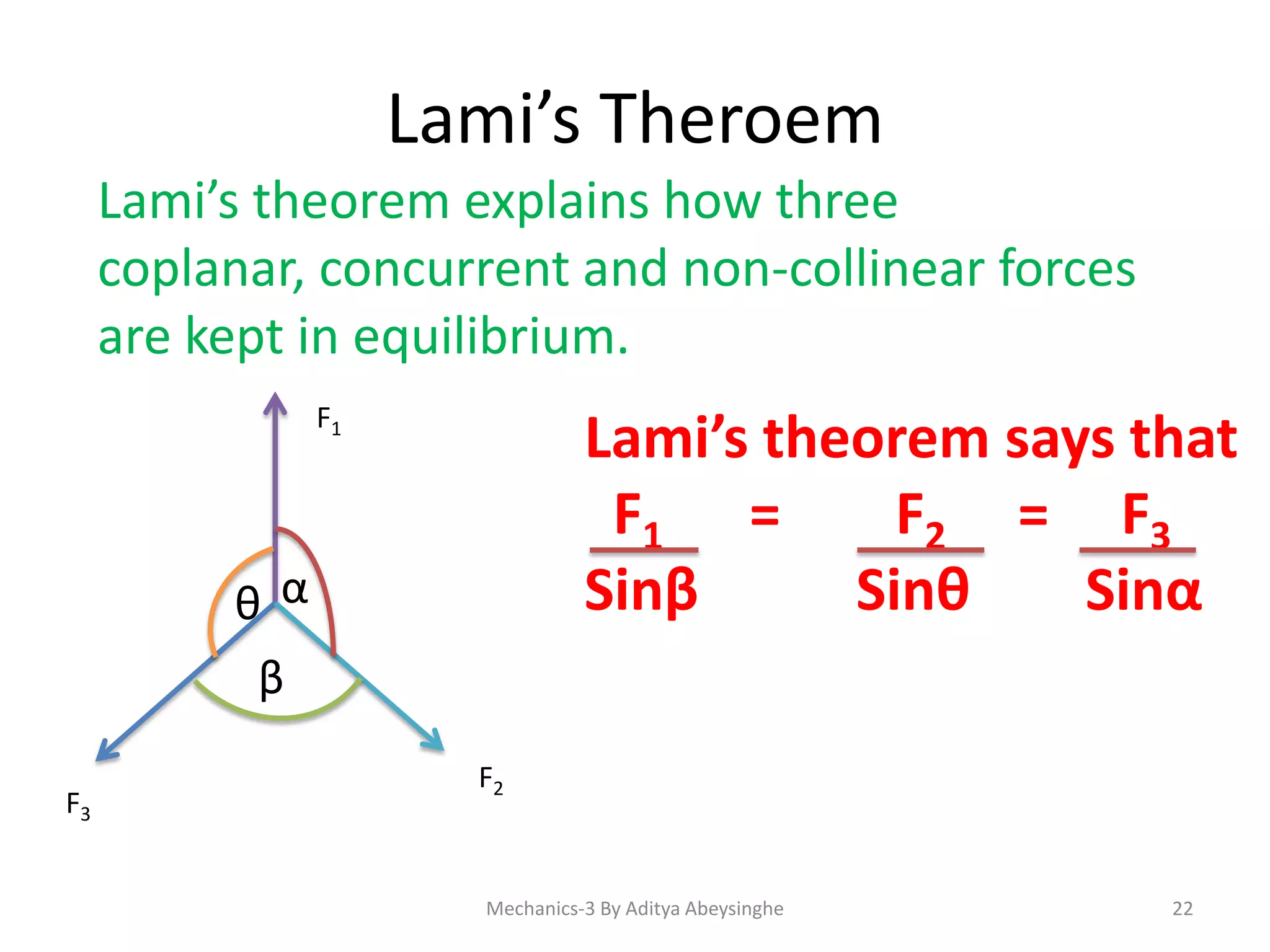
The document discusses concepts in mechanics including: - The requirements for two forces to be equal (equal in magnitude, direction, parallelism, and line of action). - The definition of moment of a force as the product of the force and its perpendicular distance from a fixed point. - Methods for calculating total moment around a point including considering direction and dividing inclined forces. 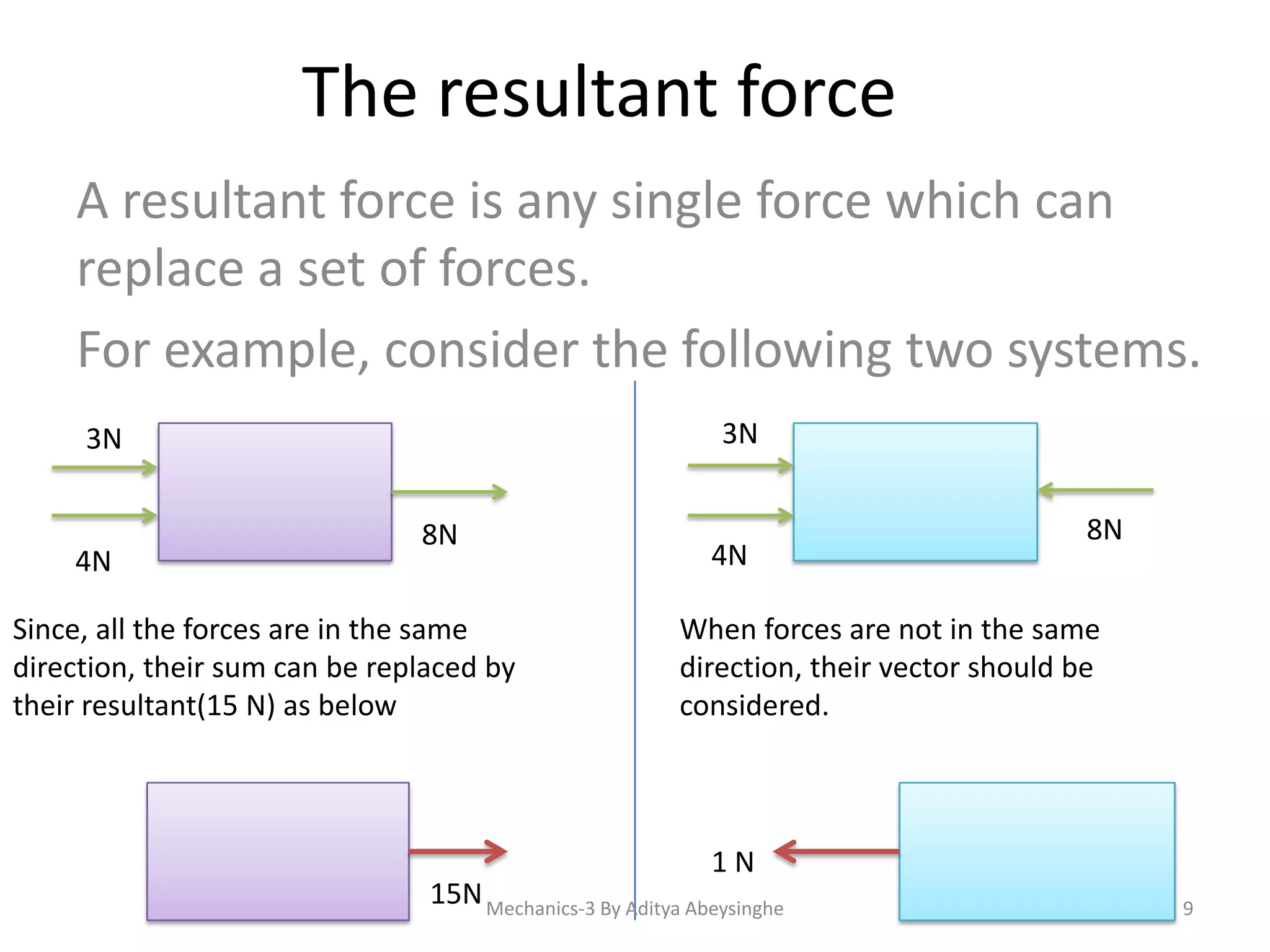- The definition of a resultant force as a single force that replaces a set of forces. 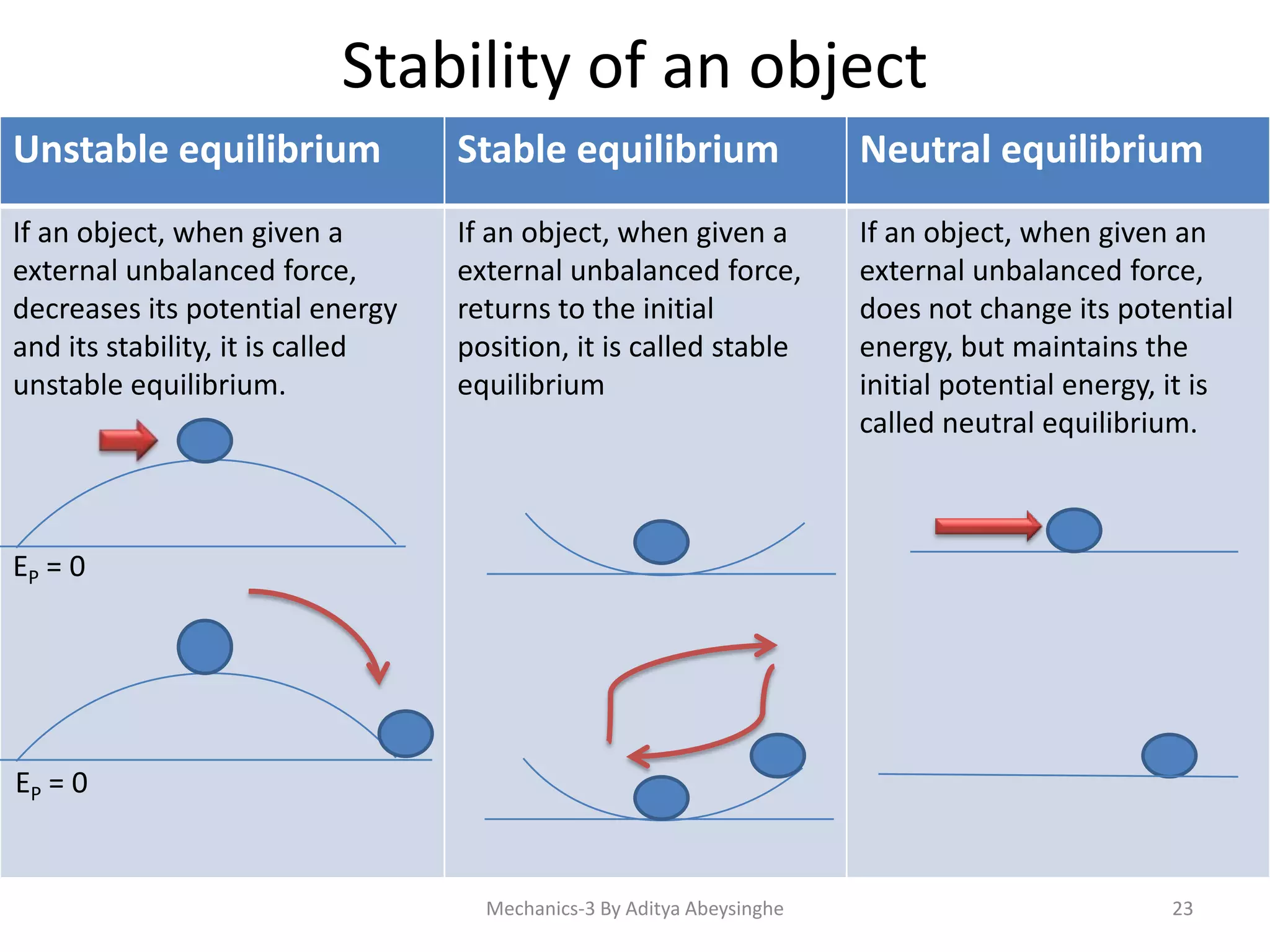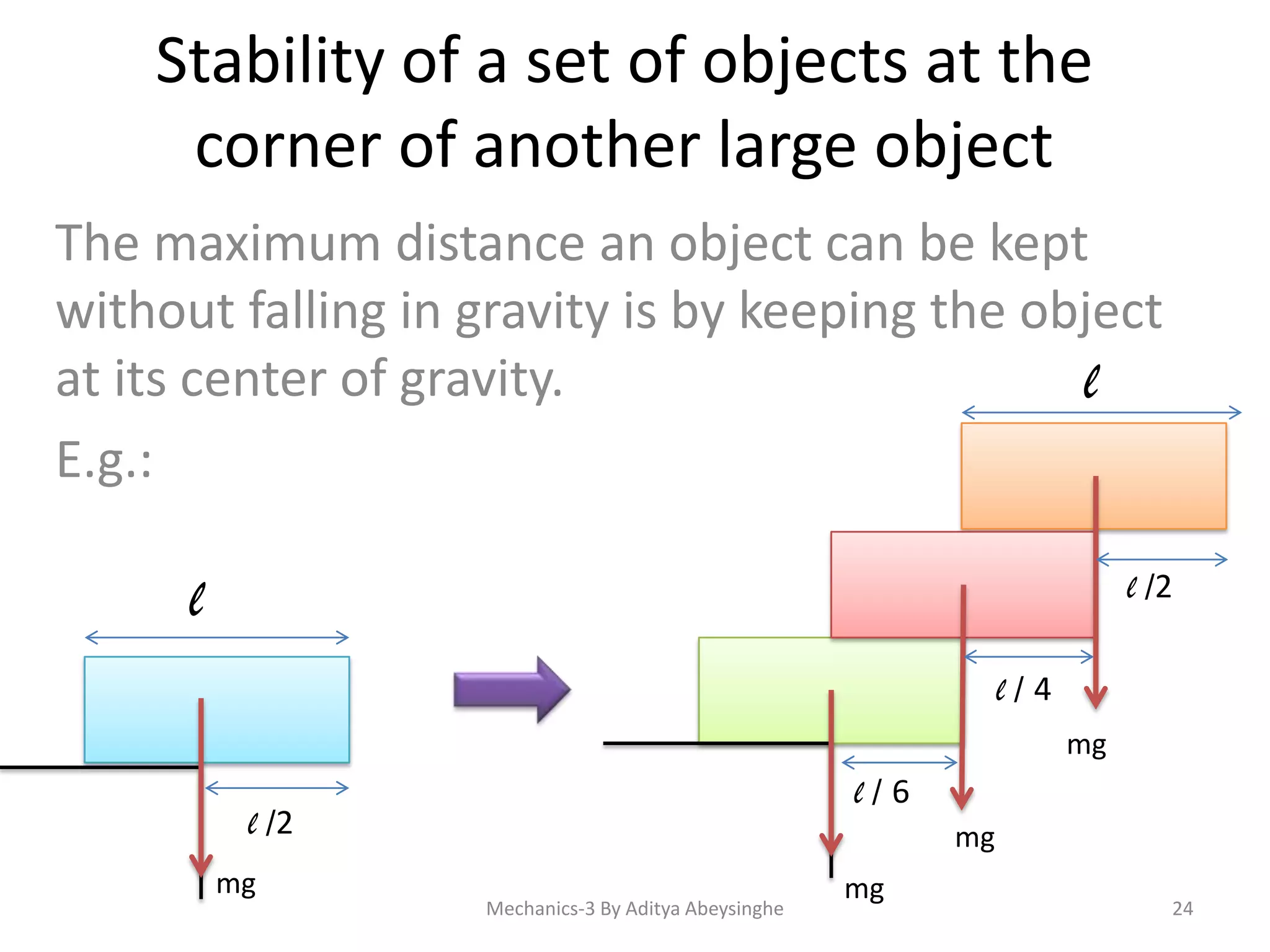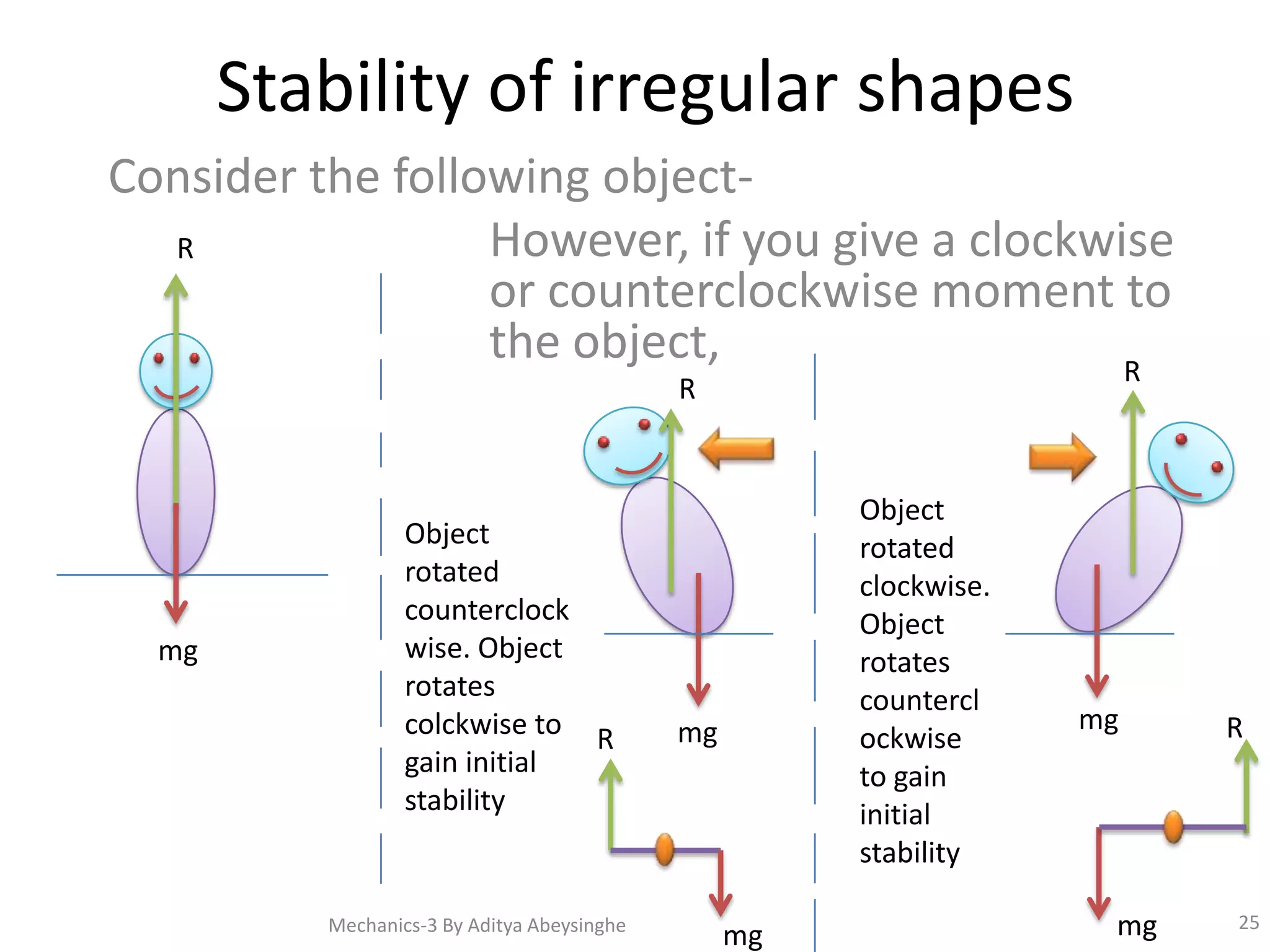- Concepts related to equilibrium including stable, unstable, and neutral equilibrium.
More Related Content
More from Aditya Abeysinghe Presentations
Mechanics 3
- 1. Mechanics - 3 Formore information about Newton’s laws and applications search the presentation- Mechanics-1 and Mechanics-2 By Aditya Abeysinghe Mechanics-3 By Aditya Abeysinghe 1
- 2. Characteristics of forces Mechanics-3By Aditya Abeysinghe 2
- 3. Requirements for twoforces to be equal F F For two forces to be equal, they should be: 1. Equal in magnitude 2. Of the same direction 3. Parallel (should display the same inclination) 4. In the same line of action Mechanics-3 By Aditya Abeysinghe 3
- 4. Moment of aforce Moment of a force around a fixed distance is the product of the force and the perpendicular distance between the force and the fixed point. That is if the force is F , the perpendicular distance between the force and the fixed point is d, Then, the moment = F × d (Note:Moment is a vector quantity – should also consider direction in calculations) Moment around O, F M=F×d d Direction- Anticlockwise O or Mechanics-3 By Aditya Abeysinghe Counterclockwise 4
- 5. E.g.: Find the totalmoment around A in the following figure. F1 D F5 C F2 F3 A F4 B Thus, the moment around point A is, GA = F2 d – F1d = (F2 - F1) d First, since forces F3 , F4 and F5 go through A, the distance between these forces and A is zero. Thus, the moment of forces around A is also zero.So, these can be ignored when calculating the moment around A. Second, we should categorize which forces create a clockwise moment around A and which forces create a counterclockwise or anticlockwise moment around A. Then, one type of moment should be taken as positive and the other type as negative when adding the moments. In this example, I have taken the clockwise direction as positive. Consider ABCD to be a square with a side’s length d. Mechanics-3 By Aditya Abeysinghe 5
- 6. If you arehaving trouble with the direction, consider ABCD as follows: F1 D F5 F3 C Counterclockwise or anticlockwise direction F1 F2 d A F4 F2 B Thus, the moment around A, A d GA = F2 d (Clockwise) + F1d (anticlockwise or counterclockwise) Clockwise direction Taking clockwise direction as positive, GA = F2 d (Clockwise) - F1d (Clockwise) Thus, the moment around A is, GA = F2 d – F1d = (F2 - F1) d. Mechanics-3 By Aditya Abeysinghe 6
- 7. However, if youtake the moment around D in either direction, you will also have to consider the inclined force, F3. In such a scenario, the moment can be calculated using two ways. 1. By taking the perpendicular distance into account and then calculating the moment. F1 D F5 F3 A F4 C F2 The perpendicular distance between F3 and D can be found to be d/√2. Thus, the clockwise moment around D is, GD = F2d – F4d – F3d/ √2 B Mechanics-3 By Aditya Abeysinghe 7
- 8. 2. Dividing theinclined force into its vertical and horizontal constituents and then taking the moment around D. F1 D F5 F3 C F2 F5 45° A F1 D C F2 F3 Sin 45° F4 B A F3 Cos 45° F4 B Since F3 Sin 45° goes through D, its effect can be minimized. Thus, the clockwise moment around D is, GD = F2d – F4d – F3 Cos45° d Therefore, GD = F2d – F4d – F3d/ √2 Mechanics-3 By Aditya Abeysinghe 8
- 9. The resultant force Aresultant force is any single force which can replace a set of forces. For example, consider the following two systems. 3N 3N 4N 8N Since, all the forces are in the same direction, their sum can be replaced by their resultant(15 N) as below 4N 8N When forces are not in the same direction, their vector should be considered. 1N 15N Mechanics-3 By Aditya Abeysinghe 9
- 10. If an inclinedforce is given, it should be divided into its horizontal and vertical components and then the resultant should be calculated. 8N 8 Sin 60° N 5N 5N 60° 8 Cos 60° N 6N 6N Thus, the sum of the forces in the horizontal direction , Rx = 5 + 6 + 8 Cos 60° = 15 N The sum of the forces in the vertical direction, Ry = 8 Sin 60° = 4√3 N Ry = 4√3 N Rx = 15 N Mechanics-3 By Aditya Abeysinghe 10
- 11. Now we wantto find the single force (resultant force) which can stand along from the effect of these two forces. It is clear that, if an inclined force is given, it should be divided into its horizontal and vertical components and then the resultant should be calculated. Conversely, horizontal and vertical forces can be reduced to another inclined force, which can stand out with the same effect produced by the two individual and perpendicular forces. Thus, the above problem can be simplified to, Ry = 4√3 N R Ry = 4√3 N α Rx = 15 N R2 = Rx2 + Ry2 R2 = 152 + (4√3)2 Therefore, R = 16.52 N And, Tanα = Ry / Rx = 0.4619 Mechanics-3 By Aditya Abeysinghe Therefore, α = 24.79° R Rx = 15 N Ry = 4√3 N α Rx = 15 N 11
- 12. Principle: The totalmoment exerted by the individual forces around a point is equal to the the moment exerted by the resultant of these forces around that point. Consider the following diagram: F1 D F5 F3 A Consider point A F4 C C D R F2 B α A B X According to the principle, From the above principle, The moment of forces around A = F2 d – F1d = R x Sinα. The moment of the resultant of these Mechanics-3 By Aditya Abeysinghe Thus, x can be calculated. force around A 12
- 13. E.g.: Consider thefollowing figureE D 5N 8N 6N F C 2N A 1N 4N B Taking the length of a side as 4 m, Calculate the following: i. Moment around points D and F. ii. The resultant of the system iii. The point where the resultant intersects the system. Mechanics-3 By Aditya Abeysinghe 13
- 14. The system canbe expanded as follows: E 5N D 8 Sin60° 6 Sin60° 8 Cos60° 6 Cos60° C F 2 Sin60° 1 Sin60° 2 Cos60° 1 Cos60° A 4N B Rx = 4 + 1 Cos60° - 6 Cos60° -5 + 8 Cos60° - 2 Cos60° = 3.5 N Thus, the clockwise moment about D = -(8 Cos60° × 2√3 ) + (8 Sin60° × 2) + (2 Sin60° × 4) + (2 Cos60° × 4√3) – (4 × 4) – (1 Cos60° × 4√3) = -5.62 Nm (counterclockwise direction) Therefore, moment about D = 5.62 Nm Thus, the counterclockwise moment about F = ( 5 × 2√3) + (4 × 2√3) + 6Sin60° × 8 + (1 Sin60° × 6) + (1 Cos60° × 2√3) = 79.67 Nm(counterclockwise direction) Therefore, moment about F = 79.67 Nm Ry = 2 Sin60° + 1 Sin60° + 6 Sin60° + 8 Sin60° = 14.72 N Mechanics-3 By Aditya Abeysinghe 14
- 15. RY = 14.72N R Thus,the resultant is, R2 = RX2 + RY2 = (3.5 N)2 + (14.72N)2 Therefore, R α RX= 3.5 N = 15.13 N and α = 77° To find where the resultant intersects the system, the system can be symplified as, D E E D 5N 8N 6N F F R C 2N A 1N 4N C α A B The moment of forces around A = The moment of the resultant of these force around A 5.62 Nm = R Sinα × (4 – x) – R CosαMechanics-3Solving Abeysinghe 2.03 m × 4√3 . By Aditya this, x = B X Therefore, the resultant intersects 15 2.03m right of A.
- 16. Center of mass Thecenter of mass on any object is any point where the total mass of the object is concentrated. The center of mass of a simple laminar body can be calculated as follows: Step 1: Tie the body to a fixed point so that the tesion of the string is equal to the weight of the body. Step 2: Rotate the object by some degrees either in the clockwise direction or in the counterclockwise/anticlockwise direction and follow step 1. Mechanics-3 By Aditya Abeysinghe 16
- 17. Weight line fromstep 1 Weight line from step 2 The intersection point of these two lines indicates the center of mass Thus, center of mass can also be described as the equilibrium point in which a particular object can be balanced in one or more ways. Mechanics-3 By Aditya Abeysinghe 17
- 18. Centers of gravityof some basic shapes G G G x G G 2x Unlike in other shapes, in a triangle the center of gravity lies in a 2:1 ratio from its Mechanics-3 By Aditya Abeysinghe weight/median line. 18
- 19. Finding the centerof gravity of a combined object E.g.: What is the center of gravity of the following object. 0.1 m G1 0.05 m If O is the center of gravity G2 x2 x1 G1 And R the resultant of masses O G2 Taking clockwise moment about O, m2g x2 - m1g x1 = 0 m1x1 = m2x2 x1 / x2 = m2/ m1 Therefore, x1 / x2 = ¼. But, x1 + x2 = 15 cm. Therefore, x1 = 3cm and x2 = 12 cm. Thus, the center of gravity lies 3cm right of Mechanics-3 By Aditya Abeysinghe G m1 g R m2 g If the mass of 1cm2 is m, Then, m1 = m × π × 102 And, m2 = m × π × 52 Therefore, m2 / m1 = 1/4 19
- 20. Equilibrium of anobject By two forces By three forces By four or more forces The two forces should be1. Equal in magnitude 2. Opposite in direction 3. Linear or in the same line of action F The resultant of any two forces should be – 1. Equal in magnitude To the 2. Opposite in direction third 3. Linear force Resultant of the all of the forces should be zero. (∑ R = 0) F1 R F2 F1 R The moment around any point should be zero. F2 (∑ (F× d) = 0 ) F F3 F3 Mechanics-3 By Aditya Abeysinghe 20
- 21. Some special definitions 1.Coplanar forces Coplanar forces are forces that lie in the same plane. 2. Concurrent forces Are three or more forces which meet at a common point or insect each other at the same point. 3. Collinear forces Are forces that occupy the same line, either parallel or not parallel to each other.(line of action is same) Mechanics-3 By Aditya Abeysinghe 21
- 22. Lami’s Theroem Lami’s theoremexplains how three coplanar, concurrent and non-collinear forces are kept in equilibrium. F1 Lami’s theorem says that F1 = F2 = F3 Sinβ Sinθ Sinα θα β F3 F2 Mechanics-3 By Aditya Abeysinghe 22
- 23. Stability of anobject Unstable equilibrium Stable equilibrium Neutral equilibrium If an object, when given a external unbalanced force, decreases its potential energy and its stability, it is called unstable equilibrium. If an object, when given a external unbalanced force, returns to the initial position, it is called stable equilibrium If an object, when given an external unbalanced force, does not change its potential energy, but maintains the initial potential energy, it is called neutral equilibrium. EP = 0 EP = 0 Mechanics-3 By Aditya Abeysinghe 23
- 24. Stability of aset of objects at the corner of another large object The maximum distance an object can be kept without falling in gravity is by keeping the object at its center of gravity. l E.g.: l l /2 l/4 mg l/6 l /2 mg mg Mechanics-3 By Aditya Abeysinghe mg 24
- 25. Stability of irregularshapes Consider the following objectHowever, if you give a clockwise R or counterclockwise moment to the object, R R mg Object rotated counterclock wise. Object rotates colckwise to R gain initial stability Mechanics-3 By Aditya Abeysinghe Object rotated clockwise. Object rotates countercl ockwise to gain initial stability mg mg mg mg R 25