AT
Uploaded byAS.A2 Physics Tutor
PPTX, PDF4,376 views

A Level Physics

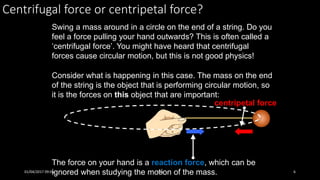
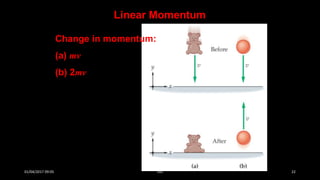
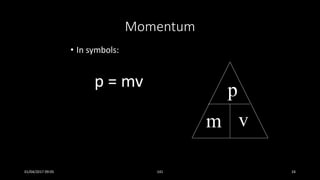
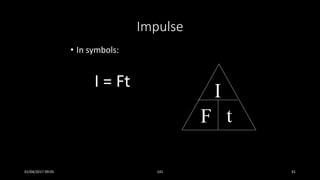
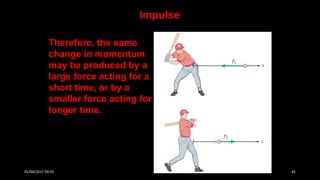
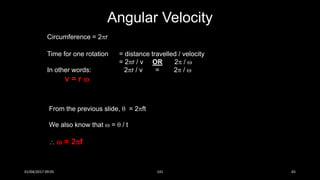
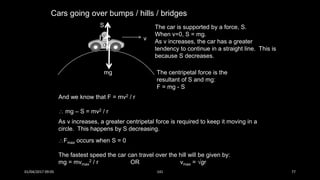
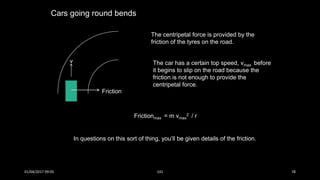
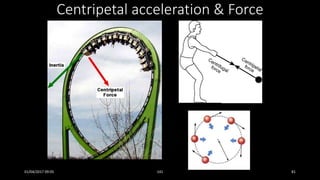
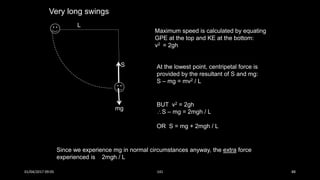
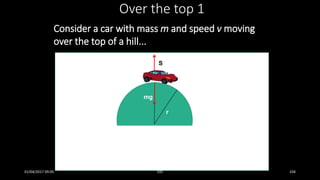
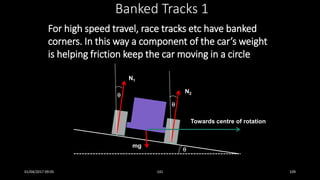
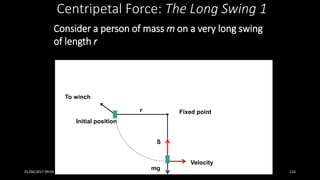
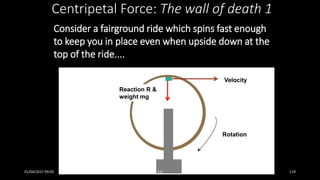
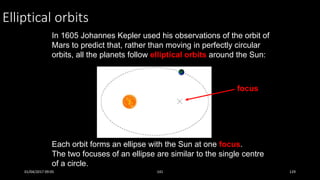
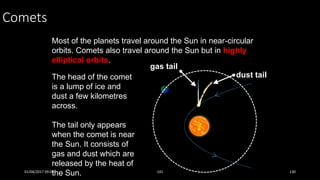
This document discusses the concepts of periodic and circular motion, focusing on momentum and its conservation. It explains how forces and acceleration influence motion, particularly in circular dynamics where centripetal force is essential. Additionally, it outlines the principles of impulse, momentum changes, and the implications of collisions and external forces on momentum conservation.

Embed presentation

Downloaded 160 times
1 / 141
2 / 141
3 / 141
4 / 141
5 / 141
6 / 141
7 / 141
8 / 141
9 / 141
10 / 141
11 / 141
12 / 141
13 / 141
14 / 141
Most read
15 / 141
16 / 141
17 / 141
18 / 141
19 / 141
20 / 141
21 / 141
22 / 141
23 / 141
24 / 141
25 / 141
26 / 141
27 / 141
28 / 141
29 / 141
30 / 141
31 / 141
32 / 141
33 / 141
34 / 141
35 / 141
36 / 141
37 / 141
38 / 141
39 / 141
40 / 141
41 / 141
42 / 141
43 / 141
44 / 141
45 / 141
46 / 141
47 / 141
48 / 141
49 / 141
50 / 141
51 / 141
52 / 141
53 / 141
54 / 141
55 / 141
56 / 141
57 / 141
58 / 141
59 / 141
60 / 141
61 / 141
62 / 141
63 / 141
64 / 141
65 / 141
66 / 141
Most read
67 / 141
Most read
68 / 141
69 / 141
70 / 141
71 / 141
72 / 141
73 / 141
74 / 141
75 / 141
76 / 141
77 / 141
78 / 141
79 / 141
80 / 141
81 / 141
82 / 141
83 / 141
84 / 141
85 / 141
86 / 141
87 / 141
88 / 141
89 / 141
90 / 141
91 / 141
92 / 141
93 / 141
94 / 141
95 / 141
96 / 141
97 / 141
98 / 141
99 / 141
100 / 141
101 / 141
102 / 141
103 / 141
104 / 141
105 / 141
106 / 141
107 / 141
108 / 141
109 / 141
110 / 141
111 / 141
112 / 141
113 / 141
114 / 141
115 / 141
116 / 141
117 / 141
118 / 141
119 / 141
120 / 141
121 / 141
122 / 141
123 / 141
124 / 141
125 / 141
126 / 141
127 / 141
128 / 141
129 / 141
130 / 141
131 / 141
132 / 141
133 / 141
134 / 141
135 / 141
136 / 141
137 / 141
138 / 141
139 / 141
140 / 141
141 / 141
3.6.1 Periodic motion 3.6.1.1 Circular motion Review of Momentum 01/04/2017 09:05 141 1
Momentum and its conservation A review from AS work 01/04/2017 09:05 141 2
Forces and acceleration This will cause an acceleration in the direction of the stronger force. This can make an object slow down or speed up, or it can cause it to change direction. An object will remain stationary or will move in the same direction at a constant speed, unless the forces acting on it are not balanced. 01/04/2017 09:05 141 3
Acceleration in a circle A motorbike drives round a corner at a constant speed. Its direction changes as it goes round the corner, so even though its speed is constant, it must be accelerating. This acceleration must be at right angles (perpendicular) to the direction of movement as it turns the corner, otherwise its speed could not be constant. Which way do you think the motorbike is accelerating, towards the inside of the bend, or away from it? 01/04/2017 09:05 141 4
Force and acceleration are both vector quantities, unlike mass, so according to this equation, their directions must be equal. Forces causing circular motion m × aF = Any object that moves in a circle must be accelerating towards the centre of that circle. What causes this? What equation do you know that links force and acceleration? All circular motion must therefore be caused by a force acting towards the centre of the circle. This type of force is known as a centripetal force.01/04/2017 09:05 141 5
Centrifugal force or centripetal force? Swing a mass around in a circle on the end of a string. Do you feel a force pulling your hand outwards? This is often called a ‘centrifugal force’. You might have heard that centrifugal forces cause circular motion, but this is not good physics! The force on your hand is a reaction force, which can be ignored when studying the motion of the mass. Consider what is happening in this case. The mass on the end of the string is the object that is performing circular motion, so it is the forces on this object that are important: centripetal force 01/04/2017 09:05 141 6
Thinking about circular motion A washing machine dries clothes by spinning them round very fast: It is important to think of circular motion as an object being continuously prevented from moving in a straight line, rather than as if the object is being flung outwards from the centre. The sides of the drum provide the centripetal force that keeps the clothes moving in a circle, but water is free to escape in straight trajectories through the holes in the sides. 01/04/2017 09:05 141 7
Momentum and its conservation 01/04/2017 09:05 141 8
Momentum and its conservation 01/04/2017 09:05 141 9
Symbol for momentum is p Unit: kg m s-1 Vector Momentum (p) is what ? Momentum (p) is the mass of an object multiplied by its velocity. momentum (p) = mass × velocity momentum (p) = mv When direction is not an important factor, how can we represent momentum? momentum = mass × speed Momentum 01/04/2017 09:05 141 10
It is harder to stop a large truck than a small car when both are moving at the same speed. The truck has more momentum than the car. By momentum, we mean inertia in motion. Momentum 01/04/2017 09:05 141 11
Momentum 01/04/2017 09:05 141 12
• A moving truck has more momentum than a car moving at the same speed because the truck has more mass. • A fast car can have more momentum than a slow truck. • A truck at rest has no momentum at all. • Next: A truck rolling down a hill Momentum 01/04/2017 09:05 141 13
A truck rolling down a hill has more momentum than a roller skate with the same speed. But if the truck is at rest and the roller skate moves, then the skate has more momentum. Momentum 01/04/2017 09:05 141 14
Can you think of a case where a roller skate and a truck would have the same momentum? Momentum Answer: The roller skate and truck can have the same momentum if the speed of the roller skate is much greater than the speed of the truck. For example, a 1000-kg truck backing out of a driveway at 0.01 ms-1 has the same momentum as a 1-kg skate going 10 ms-1. Both have momentum = 10 kg ms-1. 01/04/2017 09:05 141 15
When objects collide, assuming that there are no external forces, then momentum is always conserved.... Definition : When two or more objects interact, the total momentum remains constant provided that there is no external resultant force Conservation of Momentum 1 Mass 75 kg Velocity 4 ms-1 Mass 50 kg Velocity 0 ms-1 Mass 125 kg Velocity ??? ms-1 Mass 125 kg Velocity 2.4 ms-1 01/04/2017 09:05 141 16
Conservation of Momentum 1 01/04/2017 09:05 141 17
The force or impulse that changes momentum must be exerted on the object by something outside the object. • Molecular forces within a football have no effect on the momentum of the football. • A push against the dashboard from inside does not affect the momentum of a car. These are internal forces. They come in balanced pairs that cancel within the object. Conservation of Momentum 01/04/2017 09:05 141 18
Which is more effective at demolishing a wall? A 1kg metal ball moving at 50ms-1 Or a 1000kg ball moving at 1ms-1 Momentum 01/04/2017 09:05 141 19
Which is more effective at demolishing a wall? 1kg x 50ms-1 = 50 kg.ms-1 1000kg x 1ms-1= 1000 kg.ms-1 Momentum  01/04/2017 09:05 141 20
Momentum 01/04/2017 09:05 141 21
Linear Momentum Change in momentum: (a) mv (b) 2mv 01/04/2017 09:05 141 22
Momentum The momentum of an object: depends on what? Depends on the object’s mass. Momentum is directly proportional to what ? Momentum is directly proportional to mass. What does the object’s movement depend on ? Depends on the object’s velocity. Momentum is directly proportional to what ? Momentum is directly proportional to velocity. 01/04/2017 09:05 141 23
Momentum • In symbols: p = mv p m v 01/04/2017 09:05 141 24
Example 1 A cow of mass 640kg charges after a man at 7m s-1 to steal his crisps. What is the momentum of the cow? Write down the physics P = mv Using standard notation: m = 640kg v = 7m s-1 p = mv = 640 x 7 = 4 480 kg m s-1 01/04/2017 09:05 141 25
Example 2 Highly-trained assassin hamsters in the Amazon rainforest can run at a top speed of 62.22 m s-1 (140 mph). One such hamster has a momentum of 156 kg m s-1. What is the mass of the hamster? Using standard notation: v = 62.22 m s-1 p = 156 kg m s-1 p = mv m = p / v = 156 / 62.22 = 2.5 kg One hefty hamster! Write down the physics P = mv 01/04/2017 09:05 141 26
How do we end up with F = ma ? N2 says that the rate of change of momentum is proportional to the force OR force is proportional to the change of momentum per second. So, consider an object of mass, m, with a force, F, on it. It will accelerate from velocity u to velocity v. Initial momentum = mu. Final momentum = mv. Δp = mv – mu According to N2, F is proportional to Δp per second.  F    BUT a = (v-u) / t  F  ma OR F = kma If we define the newton as the force required to accelerate 1 kg by 1 m s-2, we get: F = ma Δp time taken mv - mu t m (v – u) t 01/04/2017 09:05 141 27
Using Newton’s Second Law You would generally give Newton’s second law as: F = If mass remains constant: F = OR F = ma If mass is changing: F = where Δm / Δt is the mass change per second Δ (mv) Δt m Δv Δt v Δm Δt 01/04/2017 09:05 141 28
Worked example Our 2.5kg psychopathic hamster Amazonian assassin. He is cruising along at 60 m s-1 when he approaches his victim. He uses his super fur-brakes to apply a braking force of 12N. How long does it take until the hamster has stopped? Using standard notation: m = 2.5kg Δv = 60 m s-1 F = 12N Newton 2: F = m Δv / Δt Δt = m Δv / F = 2.5 x 60 / 12 = 12.5s 01/04/2017 09:05 141 29
The hamster attacks its prey by firing 3kg of acid in 2s at the poor animal. It doesn’t stand a chance. But the hamster has to hang on tightly to a tree because it is pushed backwards by the force needed to fire its deadly liquid. If the hamster is able to hold on with a maximum grip of 30N, how fast can he fire his acid? Using standard notation: F = 30N Δm = 3kg Δt = 2s Newton 2: F = v Δm / Δt v = F Δt / Δm = 30 x 2 / 3 = 20 ms-1 01/04/2017 09:05 141 30
Impulse and Impact Forces 01/04/2017 09:05 141 31
The longer a force acts on an object, the greater its effect. Air rifles can fire much further than air pistols (partly) because the barrels are longer. Pistol Rifle 01/04/2017 09:05 141 32
Impulse = F Δt = Δ (mv) impulse = what changes ? impulse = change of momentum Unit usually given as ? Unit usually given as N s - but could be given as ? Unit usually given as N s - but could be given as kg m s-1 01/04/2017 09:05 141 33
Worked example A tennis ball of mass 0.20kg moving at a speed of 18ms-1 was hit by a bat, causing the ball to go back in the direction it came from at a speed of 15ms-1. The contact time was 0.12s. Calculate: a the change of momentum of the ball; b the impact force on the ball. Using standard notation: m = 0.20kg u = 18ms-1 v = -15ms-1 a change of momentum = m(v-u) = 0.20 (-15-18) = -6.6kgms-1 b F = change of momentum / time taken = -6.6 / 0.12 = -55N 01/04/2017 09:05 141 34
Force-time graphs (see notes) If a force acts on an object for a certain time, the object’s momentum will change. We can draw a force-time graph for the object. E.g. During take-off, an aeroplane’s engines exert a force of 5kN for 20s. Force Time What can you tell from the graph? The area under a force-time graph tells you the impulse (or change in momentum). 01/04/2017 09:05 141 35
Impact Forces (see notes) An impact force changes the momentum of an object. The force is given by: F = mv - mu t 01/04/2017 09:05 141 36
Worked example A ball of mass 0.63kg, initially at rest, was struck by a bat which gave it a velocity of 35ms-1. The contact time between the bat and the ball was 25ms. Calculate: a the momentum gained by the ball; b the average force of impact on the ball. Using standard notation: m = 0.63kg v = 35ms-1 t = 0.025s a p = mv = 0.63 x 35 = 22kgms-1 b Using impulse: Ft = Δmv F = Δmv / t = 22 / 0.025 = 880N 01/04/2017 09:05 141 37
If an object hits a wall at an angle, you only need to consider the components of velocity in the direction of the force.   u cos  v cos  When an object rebounds after impact, be very careful with directions of F, m and v. A couple of points to bear in mind 01/04/2017 09:05 141 38
Impulse • The impulse exerted on an object depends on: • The force acting on the object. • Impulse is directly proportional to force. • The time that the force acts. • Impulse is directly proportional to time. 01/04/2017 09:05 141 39
Definition : The impulse of a force is defined as the product of the force and the time which the force acts for The impulse = Ft = mv The impulse of the force acting upon an object is equal to the change of momentum for the force Impulse of a Force 01/04/2017 09:05 141 40
Impulse • In symbols: I = Ft I F t 01/04/2017 09:05 141 41
Impulse 01/04/2017 09:05 141 42
Collisions – Example 1 •Collisions may be the result of direct contact. •The impulsive forces may vary in time in complicated ways. • This force is internal to the system. • Observe the variations in the active figure. •Momentum is conserved. 01/04/2017 09:05 141 43
Collisions – Example 2 •The collision need not include physical contact between the objects. •There are still forces between the particles. •This type of collision can be analysed in the same way as those that include physical contact. 01/04/2017 09:05 141 44
Impulse Therefore, the same change in momentum may be produced by a large force acting for a short time, or by a smaller force acting for a longer time. 01/04/2017 09:05 141 45
Impulse Impulse is a what type of quantity? Impulse is a vector quantity. Common units of impulse are ? Common units of impulse: N s 01/04/2017 09:05 141 46
When a dish falls, will the impulse be less if it lands on a carpet than if it lands on a hard floor? True or false ? Impulse Changes Momentum Answer: False. The impulse would be the same for either surface because the same momentum change occurs for each. It is the force that is less for the impulse on the carpet because of the greater time of momentum change. 01/04/2017 09:05 141 47
Impulse & Momentum The impulse exerted on an object equals the object’s what? (in terms of momentum) ? The impulse exerted on an object equals the object’s change in momentum 01/04/2017 09:05 141 48
Impulse & Momentum 01/04/2017 09:05 141 49
Impulse & Momentum • In symbols: I = p 01/04/2017 09:05 141 50
Impulse-Momentum: Crash Test Example •Conceptualize • The collision time is short. • We can image the car being brought to rest very rapidly and then moving back in the opposite direction with a reduced speed. •Categorise • Assume net force exerted on the car by wall and friction with the ground is large compared with other forces. • Gravitational and normal forces are perpendicular and so do not effect the horizontal momentum. 01/04/2017 09:05 141 51
Impulse physics problem solved 01/04/2017 09:05 141 52
Collisions and Explosions Objective • Be able to apply the principle of conservation of momentum to explosions and collisions. 01/04/2017 09:05 141 53
Conservation of Momentum Consider several objects which interact with each other. If there is no external force, tells us that there will be no change in momentum. BUT momentum can be transferred between the objects. When doing problems involving collisions or explosions, just work out the momentum at the start and equate it with the momentum at the end. Principle of conservation of momentum: for a system of interacting objects, the total momentum remains constant, provided no external resultant force acts on the system. In English, this means: total momentum before = total momentum after 01/04/2017 09:05 141 54
Worked example A sheep of mass 100kg is out for a run one day. He picks up speed until he reaches 8ms-1, when he runs into a stationary shopping trolley of mass 20kg. The force of the impact slows our sheep to 6ms-1, and causes the trolley to start moving. What is the velocity of the trolley immediately after impact? Using standard notation: Sheep: ms = 100kg us = 8ms-1 vs = 6ms-1 Trolley: mt = 20kg ut = 0ms-1 Total initial momentum = initial momentum of sheep + initial momentum of trolley = (100 x 8) + (20 x 0) = 800kgms-1 Total final momentum = final momentum of sheep + final momentum of trolley = (100 x 6) + (20 x vt) = 600 + 20vt Using principle of conservation of momentum: 800 = 600 + 20vt vt = 10ms-1 01/04/2017 09:05 141 55
Energy in Collisions 01/04/2017 09:05 141 56
Three types of collision: Elastic No kinetic energy is lost in the collision (dropped ball rebounds to original height) Totally inelastic The objects stick together (railway wagons) Partially elastic The objects move apart but have less kinetic energy than before (cars colliding) Reminder: KE = ½ mv2 Remember: Momentum is ALWAYS conserved in a collision. KE may be converted to other forms of energy. Where does all the KE disappear to? 01/04/2017 09:05 141 57
Worked example Buzz Lightyear has a mass of 160kg in his space suit. He flies straight at Zurg at 40ms-1. Zurg is a baddie so, although he has 20kg more mass that Buzz, he can only fly at 30ms-1, and he is doing this – straight towards Buzz! Assuming they stick together in one tousling lump, calculate: a the speed and direction of Buzz and Zurg immediately after impact; b the loss of kinetic energy due to the impact. Using standard notation: mB = 160kg uB = 40ms-1 mZ = 180kg uZ = - 30ms-1 a Initial momentum = (160 x 40) - (180 x 30) = 1000kgms-1 Final momentum = (160 + 180) v Using principle of conservation of momentum: 1000 = 340v v = 2.94ms-1 in the direction in which Buzz was initially travelling. b KE before impact = (0.5 x 160 x 40 x 40) + (0.5 x 180 x -30 x -30) = 209kJ KE after impact = (0.5 x 340 x 2.94 x 2.94) = 1.5kJ Loss of KE = 207.5kJ 01/04/2017 09:05 141 58
Circular motion 01/04/2017 09:05 141 59
Circular motion 01/04/2017 09:05 141 60
Angles can be measured in both degrees & radians : Radians & Degrees The angle  in radians is defined as the arc length / the radius For a whole circle, (360°) the arc length is the circumference, (2r)  360° is 2 radians  Arc length r Common values : 45° = /4 radians 90° = /2 radians 180° =  radians Note. In S.I. Units we use “rad” 01/04/2017 09:05 141 61
Angular velocity, for circular motion, has counterparts which can be compared with linear speed s=d/t. Time (t) remains unchanged, but linear distance (d) is replaced with angular displacement  measured in radians. Angular Displacement  Angular displacement  r r Angular displacement is the number of radians moved 01/04/2017 09:05 141 62
Consider a bike wheel which is rotating. In order to do useful calculations, we need to talk about angular displacement and angular velocity.  = angular displacement (rad) = angular velocity (rad s-1) If the wheel takes T seconds to rotate once, it will turn through an angle of 2 / T radians each second. The frequency of rotation will be given by f = 1/T The angular displacement in a certain amount of time, t, is given by:  = 2t / T OR  = 2ft Angular Displacement 01/04/2017 09:05 141 63
Consider an object moving along the arc of a circle from A to P at a constant speed for time t: Angular Velocity : Definition Definition : The rate of change of angular displacement with time “The angle, (in radians) an object rotates through per second”  =  / t  Arc length r r P A This is all very comparable with normal linear speed, (or velocity) where we talk about distance/time Where  is the angle turned through in radians, (rad), yields units for  of rads-1 01/04/2017 09:05 141 64
Circumference = 2r Time for one rotation = distance travelled / velocity = 2r / v OR 2 /  In other words: 2r / v = 2 /  v = r  Angular Velocity From the previous slide,  = 2ft We also know that  =  / t   = 2f 01/04/2017 09:05 141 65
Worked example A cyclist travels at a speed of 12 ms-1 on a bike which has wheels of radius 40cm. Calculate: a the frequency of rotation of each wheel; b the angular speed of each wheel; c the angle the wheel turn through in 0.10s in: i radians ii degrees Using standard notation: v = 12ms-1 r = 0.4m a circumference = 2 x  x 0.4 = 2.5m T = circumference / speed = 2.5 / 12 = 0.21s f = 1 / T = 1 / 0.21 = 4.8Hz b  = 2f = 30rads-1 c i  = t = 30 x 0.1 3.0rad ii  = 3.0 x 360 / 2 = 1720 01/04/2017 09:05 141 66
The period T of the rotational motion is the time taken for one complete revolution (2 radians). Angular Velocity : Period & Frequency Substituting into :  =  / t (angular speed) f = 1/T and  = 2f (see notes) Substituting for f :  = 2 / T T = 2 /  From our earlier work on waves we know that the period (T) & frequency (f) are related T = 1/f f =  / 2 01/04/2017 09:05 141 67
Considering the diagram below, we can see that the linear distance travelled is the arc length Angular Velocity : linear speed Linear speed (v) = arc length (AP) / t v = r / t Substituting... ( =  / t) v = r  Arc length r r P A 01/04/2017 09:05 141 68
A cyclist travels at a speed of 12ms-1 on a bike with wheels which have a radius of 40cm. Calculate: a. The frequency of rotation for the wheels b. The angular velocity for the wheels c. The angle the wheel turns through in 0.1s in i radians ii degrees Angular Velocity : Worked example 01/04/2017 09:05 141 69
The frequency of rotation for the wheels Circumference of the wheel is = = 2r (subs for r) = = 2 x 0.4m = 2.5m Time for one rotation, (the period s) is found using: ? s =d / t …. rearranged for t t = d / s = T = circumference / linear speed or T= T = 2.5 / 12 = 0.21s  f = f = 1 / T = 1 / 0.21 = 4.8Hz Angular Velocity : Worked example 01/04/2017 09:05 141 70
The angular velocity for the wheels Using T = 2 / , rearranged for   = 2 / T … subs for T  = 2 / 0.21 = ?  = 30 rads-1 Angular Velocity : Worked example 01/04/2017 09:05 141 71
The angle the wheel turns through in 0.1s in i radians ii degrees Using  =  / t re-arranged for   = t … subs for  and t  = 30 x 0.1 = ?  = 3 rad …. In degrees? = 3 x (360°/ 2) = 172° Angular Velocity : Worked example 01/04/2017 09:05 141 72
Circular motion Centripetal Force 01/04/2017 09:05 141 73
Centripetal Force If you pick any point on this bike wheel, it will rotate with a constant speed, but its direction will be constantly changing. This means its velocity is changing. It is always accelerating. This is called centripetal acceleration. Centripetal acceleration is given by: a = v2 / r = 2 r And, since it’s accelerating, there must be a force. This is called centripetal force. By applying N2, we get: F = mv2 / r = mr2 01/04/2017 09:05 141 74
Worked example A stone of mass 0.5kg is swung round in a horizontal circle (on a frictionless surface) of radius 0.75m with a steady speed of. Calculate: a the centripetal acceleration of the stone; b the centripetal force acting on the stone. Using standard notation: m= 0.5kg r= 0.75m v= 4ms-1 a) a = v2/r = 42 / 0.75 = 21.4 m s-2 b) F = ma = 0.5 x 21.4 = 10.7 N Notice that this is a linear acceleration and not an angular acceleration. The angular velocity of the stone is constant and so there is no angular acceleration.01/04/2017 09:05 141 75
Applications of Circular Motion - Cars Objective • Explain what forces are experienced when cars travel over hills and round bends. 01/04/2017 09:05 141 76
Cars going over bumps / hills / bridges S mg v The car is supported by a force, S. When v=0, S = mg. As v increases, the car has a greater tendency to continue in a straight line. This is because S decreases. The centripetal force is the resultant of S and mg: F = mg - S And we know that F = mv2 / r  mg – S = mv2 / r As v increases, a greater centripetal force is required to keep it moving in a circle. This happens by S decreasing. Fmax occurs when S = 0 The fastest speed the car can travel over the hill will be given by: mg = mvmax 2 / r OR vmax = gr 01/04/2017 09:05 141 77
Cars going round bends v Friction The centripetal force is provided by the friction of the tyres on the road. The car has a certain top speed, vmax before it begins to slip on the road because the friction is not enough to provide the centripetal force. Frictionmax = m vmax 2 / r In questions on this sort of thing, you’ll be given details of the friction. 01/04/2017 09:05 141 78
Banked tracks This is supposed to be a car coming towards us. It’s travelling round a bend and the track is banked at an angle, . mg  R Centripetal force IF there’s no friction on the tyres, the centripetal force is provided by the horizontal component of R. F = R sin (which is also equal to mv2 / r) mg is balanced by the vertical component of R, so: mg = R cos R sin R cos = mv2 rmg OR tan = v2 / gr 01/04/2017 09:05 141 79
My hamster has a mass of 2kg (he’s a big lad). He has a top speed of 15ms-1. Is he able to run over a hill of radius 20m at top speed without taking off? (g = 9.8ms-2). Worked example Say the hamster is supported by a force, S. The centripetal force is the resultant of S and mg: F = mg – S Fmax will occur when S = 0 Fmax = mg BUT centripetal force is also given by F = mv2 / r The fastest the animal can travel over the hill will be given by: mg = mvmax 2 / r vmax = gr = 14ms-1 No, he can’t run over the hill at top speed. 01/04/2017 09:05 141 80
Centripetal acceleration & Force 01/04/2017 09:05 141 81
Centripetal acceleration & Force 01/04/2017 09:05 141 82
If an object is moving in a circle with a constant speed, it’s velocity is constantly changing.... Because? Because the direction is constantly changing.... If the velocity is constantly changing then by definition the object is accelerating – what about force? If the object is accelerating, then an unbalanced force must exist Centripetal Acceleration : Introduction Velocity v 01/04/2017 09:05 141 83
Centripetal Acceleration : Proof 1 Velocity vB  Velocity vA Consider an object moving in circular motion with a speed v which moves from point A to point B in t seconds (From speed=distance / time), the distance moved along the arc AB, s is? vt Velocity vB Velocity vA v C A B  The vector diagram shows the change in velocity v : (vB – vA)01/04/2017 09:05 141 84
Centripetal Acceleration : Proof 2 Velocity vB  Velocity vA The triangles ABC & the vector diagram are similar If  is small, then v / v = s / r Velocity vB Velocity vA v C A B  Substituting for s = vt v / v = vt / r (a = change in velocity / time) a = v / t = v2 / r 01/04/2017 09:05 141 85
Applications of Circular Motion – Fairground Rides 01/04/2017 09:05 141 86
Big dippers When you go down a dip, you’re forced down into your seat. The centripetal force is the resultant of S and mg, and is also equal to mv2 / r: F = S – mg = mv2 / r  S = mg + mv2 / r S represents the support force of the track on the car. Since we experience mg in normal circumstances anyway, the extra force pushing downwards is mv2 / r 01/04/2017 09:05 141 87
L mg S Very long swings Maximum speed is calculated by equating GPE at the top and KE at the bottom: v2 = 2gh At the lowest point, centripetal force is provided by the resultant of S and mg: S – mg = mv2 / L BUT v2 = 2gh S – mg = 2mgh / L OR S = mg + 2mgh / L Since we experience mg in normal circumstances anyway, the extra force experienced is 2mgh / L 01/04/2017 09:05 141 88
Person at top R + mg Big wheel thingy On this big wheel thingy, the riders are being squished against the inside of the circumference. At the maximum height, the centripetal Force is provided by R + mg and is equal to mv2 / r R = mv2 / r - mg R is the reaction force from the wheel. At a certain speed, v0 (so that v0 2 = gr), R = 0.  There is no reaction force on the person. You must have a minimum speed of v0 to stop people falling out. 01/04/2017 09:05 141 89
Examples of centripetal forces More examples of circular motion caused by centripetal forces: Can you work out the direction of the force in each case, and describe the type of force involved? 01/04/2017 09:05 141 90
How does the centripetal force depend on mass? F = ma, so force is proportional to acceleration. If the truck is going faster, or if its radius is smaller, then it is changing direction more quickly, so its acceleration is greater. How does the centripetal force depend on speed and radius? F = ma, so force is proportional to mass. The greater the mass, the larger the centripetal force needed to maintain circular motion. The greater the speed, and the smaller the radius, the larger the centripetal force needed to maintain circular motion. Factors affecting centripetal forces 01/04/2017 09:05 141 91
Understanding centripetal forces 01/04/2017 09:05 141 92
Circular motion 01/04/2017 09:05 141 93
Centripetal Acceleration : angular We can substitute for angular velocity.... a = v2 / r We have already seen that: v = r (substituting for v into above) a = (r)2 / r or a = a = r2 01/04/2017 09:05 141 94
Centripetal Force In exactly the same way as we can connect force f and acceleration a using Newton’s 2nd law of motion, we can arrive at the centripetal force which is keeping the object moving in a circle f = mv2 / r or f = mr2 Any object moving in a circle is acted upon by a single resultant force towards the centre of the circle. We call this the centripetal force01/04/2017 09:05 141 95
Centripetal Force :Centripetal Force : Using this stuff!Centripetal Force : Gravity & Orbits 01/04/2017 09:05 141 96
Centripetal Force : Gravity & Orbits Gravity which keeps satellites in orbit around Earth and the Earth in orbit around the sun is a classic example of a centripetal force. Planet satellite Gravity 01/04/2017 09:05 141 97
The wheel of the London Eye has a diameter of 130m and takes 30mins for 1 revolution. Calculate: a. The speed of the capsule b. The centripetal acceleration c. The centripetal force on a person with a mass of 65kg Worked example 1 01/04/2017 09:05 141 98
The speed of the capsule : Using v = r we know that we do a full revolution (2 rad) in ? 30mins (1800s) v = = (130/2) x (2 / 1800) … v = v = 0.23 ms-1 Worked example 1 01/04/2017 09:05 141 99
The centripetal acceleration: Using a = v2 / r a = (0.23)2 / (130/2) a = 7.92 x 10-4 ms-2 The centripetal force: (equation?) Using f = ma F = 65 x 7.92 x 10-4 F = 0.051 N Worked example 1 01/04/2017 09:05 141 100
Centripetal Force & the Road 01/04/2017 09:05 141 101
Centripetal Force & the Road 01/04/2017 09:05 141 102
An object moving in a circle has a constantly changing velocity, it is therefore experiencing acceleration and hence a force towards the centre of rotation. What do we call this force? We called this the centripetal force: The force required to keep the object moving in a circle. In reality this force is provided by another force, e.g. The tension in a string, friction or the force of gravity. Centripetal Acceleration : Recap 01/04/2017 09:05 141 103
Consider a car with mass m and speed v moving over the top of a hill... Over the top 1 mg r S 01/04/2017 09:05 141 104
At the top of the hill, the support force S, is in the opposite direction to the weight (mg). It is the resultant between these two forces which keep the car moving in a circle mg – S = mv2 / r If the speed of the car increases, there will eventually be a speed v0 where the car will leave the ground (the support force S is 0) mg = mv0 2 / r v0 = (gr)½ Any faster and the car will leave the ground Over the top 2 01/04/2017 09:05 141 105
On a level road, when a car travels around a roundabout the centripetal force required to keep the car moving in a circle is provided by the friction between the road surface and tyres Around a Roundabout 1 velocity friction Force of Friction F F = mv2 / r 01/04/2017 09:05 141 106
Factors affecting centripetal forces 01/04/2017 09:05 141 107
To avoid skidding or slipping, the force of friction F0 must be less than the point where friction is overcome which occurs at speed v0 Friction is proportional to weight and can be given by the coefficient of friction (): F  mg F = mg At the point of slipping: F0 = mv0 2 / r  mg = mv0 2 / r  v0 = (gr)½ Around a Roundabout 2 01/04/2017 09:05 141 108
For high speed travel, race tracks etc have banked corners. In this way a component of the car’s weight is helping friction keep the car moving in a circle Banked Tracks 1 mg N1 N2    Towards centre of rotation 01/04/2017 09:05 141 109
Without any banking the centripetal force is provided by friction alone. Banked corners allows greater speeds before friction is overcome The centripetal force is provided by the horizontal components of the support forces (N1 + N2) sin  = mv2 / r and the vertical components balance the weight (N1 + N2) cos  = mg Banked Tracks 2 01/04/2017 09:05 141 110
Rearranging sin  = mv2 / (N1 + N2) r cos  = mg / (N1 + N2) and since tan  = sin  / cos  tan  = mv2 / (N1 + N2) r x (N1 + N2) / mg tan  = mv2 / mgr v2 = gr tan  Thus there is no sideways frictional force if the speed v is such that v2 = gr tan  Banked Tracks 3 01/04/2017 09:05 141 111
Centripetal Force & the Fairground 01/04/2017 09:05 141 112
Centripetal Force & the Fairground 01/04/2017 09:05 141 113
At the bottom of a big dipper you are pushed into your seat and feel “heavier”... Centripetal Force: Big Dippers 1 Centre of curvature mg velocity 01/04/2017 09:05 141 114
At the bottom of the dip at speed v with radius r, Resolving the vertical forces: S – mg = mv2 / r S = mg + mv2 / r The “extra” weight you experience when feeling “heavy” is given by the centripetal force Centripetal Force: Big Dippers 2 01/04/2017 09:05 141 115
Consider a person of mass m on a very long swing of length r Centripetal Force: The Long Swing 1 Fixed point To winch Initial position r S mg Velocity 01/04/2017 09:05 141 116
As the swing is released we can consider the conservation of energy, loss in potential energy is the gain in the kinetic energy mgh = ½mv2  v2 = 2gh The passenger is on a circular path with radius r. At the bottom of the swing the support force S acts against the person’s weight mg. This provides the centripetal force: S – mg = mv2/r Centripetal Force: The Long Swing 2 01/04/2017 09:05 141 117
Substituting for v2: S – mg = mv2/r S – mg = 2mgh/r S = mg + 2mgh/r The person “feels heavier” by 2mgh/r, if the swing drops through 90°, then the extra support force is twice the persons weight (mg) Centripetal Force: The Long Swing 3 01/04/2017 09:05 141 118
Consider a fairground ride which spins fast enough to keep you in place even when upside down at the top of the ride.... Centripetal Force: The wall of death 1 Velocity Rotation Reaction R & weight mg 01/04/2017 09:05 141 119
The wheel turns fast enough to keep the passenger in position as they pass over the top. At the top, the reaction R acts downwards and together with the weight provides the centripetal force: mg + R = mv2/ r R = mv2/ r – mg At a certain speed v0 such that v0 2 = gr, then the reaction from the wall will be zero Centripetal Force: The wall of death 2 01/04/2017 09:05 141 120
What is gravity? If a skydiver steps out of a plane, which way does he move? What causes this effect? Gravity is a universal force which attracts any mass to every other mass in the Universe. Every mass has its own gravitational field, like the one surrounding Earth, but it takes two objects to make a gravitational force. Gravity is a very weak force, so small objects don’t stick together, but if at least one mass is very large, the effect of gravity is easy to see. Skydivers always fall back to Earth!01/04/2017 09:05 141 121
Factors affecting gravity The bigger the mass, the stronger its gravitational field, so the Sun has a much stronger gravitational field than Earth. Gravitational fields are stronger:  around larger masses  at shorter distances. The gravitational force between two objects can be increased:  by increasing the size of either or both of the masses  by decreasing the distance between them. But the further apart two objects are, the weaker the gravitational forces between them. So when a skydiver jumps out of a plane, he falls to Earth, not towards the Sun! 01/04/2017 09:05 141 122
Gravitational chaos! Every mass in the universe attracts every other. That’s a lot of forces to keep track of! But gravity is a very weak force, so most gravitational forces at the Earth’s surface can be ignored. The gravitational field of a pen, a person or even a large mountain is too weak to have a noticeable effect, so the only gravitational field you need to consider is Earth’s. 01/04/2017 09:05 141 123
Gravity at the Earth’s surface Gravitational fields get weaker with increasing distance. Do you feel any lighter on the top floor of your house than on the ground floor? The Earth is so large that small changes in height don’t affect weight, so gravitational field strength is effectively constant: weight = mass × gravitational field strength This applies to objects at the Earth’s surface, at the top of a mountain, or even in an aeroplane at 30000 feet… …but be careful! This does not apply to satellites in orbit, or to the forces between planets and stars. = mass × 10 N/kg 01/04/2017 09:05 141 124
Understanding gravity 01/04/2017 09:05 141 125
Gravity as a centripetal force Examples of centripetal forces can be found in many everyday contexts, but what about circular motion on a large scale? What is the centripetal force that makes orbits possible? Unlike a mass on a string, stars and planets are not physically connected to each other, but they are attracted to each other by gravity. How does circular motion under gravity compare to the types of circular motion we are used to? 01/04/2017 09:05 141 126
Circular motion under gravity The centripetal force required to keep a planet in circular motion depends on mass, radius and speed. But the gravitational force that a star actually provides only depends on mass and radius. This means that for any specific radius, a planet must move at one specific speed to stay in orbit.  When a mass on a string is swung at an increasing speed, the tension increases, while the radius remains constant:  If a planet orbits a star at an increasing speed, the force between them does not increase, so it moves out of that orbit: 01/04/2017 09:05 141 127
Circular motion under gravity 01/04/2017 09:05 141 128
Elliptical orbits In 1605 Johannes Kepler used his observations of the orbit of Mars to predict that, rather than moving in perfectly circular orbits, all the planets follow elliptical orbits around the Sun: Each orbit forms an ellipse with the Sun at one focus. The two focuses of an ellipse are similar to the single centre of a circle. focus 01/04/2017 09:05 141 129
The head of the comet is a lump of ice and dust a few kilometres across. The tail only appears when the comet is near the Sun. It consists of gas and dust which are released by the heat of the Sun. Comets Most of the planets travel around the Sun in near-circular orbits. Comets also travel around the Sun but in highly elliptical orbits. gas tail dust tail 01/04/2017 09:05 141 130
Data analysis 01/04/2017 09:05 141 131
What is a satellite? A satellite is an object that orbits a planet. Satellites can be natural or they can be artificial. The same physics applies to satellites orbiting the Earth as to planets orbiting the Sun. The largest satellite orbiting Earth is the Moon. This is Earth’s only natural satellite. Artificial satellites are put into orbit for a range of purposes, such as mapping and surveillance. 01/04/2017 09:05 141 132
Types of orbit 01/04/2017 09:05 141 133
Uses for geostationary satellites Geostationary satellites are particularly useful because they stay fixed above a single point on Earth. This makes them useful for communications and satellite TV broadcasting, because the satellite never goes out of range. Geostationary satellites are also used for weather forecasting. Satellite dishes can be fixed to face in the correct direction, without the need to track the movement of the satellite. 01/04/2017 09:05 141 134
Problems with geostationary satellites There are some disadvantages to geostationary satellites.  All geostationary satellites must orbit over the equator at a specific altitude of 36000km. There are limited slots in this orbit, which can lead to disputes when different countries want a certain slot.  A geostationary satellite can only ‘see’ a certain area of the Earth’s surface – the rest is hidden from view.  All geostationary satellites are a long way from Earth, which causes delays in signals. This can be a disadvantage during commercial or military communications.01/04/2017 09:05 141 135
Uses for polar orbit satellites Polar satellites are particularly useful because they orbit at a low altitude and high speed. This makes them useful for mapping, as they can image the Earth’s surface in higher resolution than more distant satellites. It also makes them useful for observation purposes, such as military surveillance, or weather monitoring, as they can view the whole of the Earth’s surface in one day. However, polar satellites must be tracked from the ground, and will be out of range for much of the time, causing delays in data retrieval.01/04/2017 09:05 141 136
Which type of satellite? 01/04/2017 09:05 141 137
Glossary 01/04/2017 09:05 141 138
Anagrams 01/04/2017 09:05 141 139
Multiple-choice quiz 01/04/2017 09:05 141 140
Circular motion Questions? 01/04/2017 09:05 141 141

More Related Content

PPTX
Electricity as level
byIB School
 
PPT
forces ppt.ppt
byMashhoodAhmed9
 
PPT
2-kinematics.ppt
byRahulGupta257719
 
PDF
Physics-Unit-1.pdf
bySadmanDibbo
 
PPSX
Physical quantities and units pps
byTeacher Tanoto
 
PPTX
Topic 2 - Motion and Forces.GCSE combine science ppt
byNisbaRani2
 
PPT
211461260-Igcse-14-Momentum_2.ppt
byssuser5087b61
 
PPTX
Physics 33 electromagnetic effects 2
byNurul Fadhilah
 
Electricity as level
byIB School
 
forces ppt.ppt
byMashhoodAhmed9
 
2-kinematics.ppt
byRahulGupta257719
 
Physics-Unit-1.pdf
bySadmanDibbo
 
Physical quantities and units pps
byTeacher Tanoto
 
Topic 2 - Motion and Forces.GCSE combine science ppt
byNisbaRani2
 
211461260-Igcse-14-Momentum_2.ppt
byssuser5087b61
 
Physics 33 electromagnetic effects 2
byNurul Fadhilah
 

What's hot

PPT
Ch 9 Rotational Dynamics
byScott Thomas
 
PPT
Center Of Mass
byGillianWinters
 
PPTX
Linear motion of a particle
byKhanSaif2
 
PPTX
Displacement and Velocity
bymlong24
 
PPTX
Electrostatics
bySeyid Kadher
 
PPT
Coulombs Law
bywilsonphysics
 
PPTX
Electric Field & Electric Potential
byKC College
 
PPT
Momentum
bySells Middle School
 
PPT
Oscillations
byJulieber Bersabe
 
PPTX
Conservation Laws
bySepti Pramuliawati
 
PPTX
Magnetism and Electromagnetism
byShafie Sofian
 
PPT
Electric Fields
byChris Staines
 
PPT
1.1.1 gravitational fields
byJohnPaul Kennedy
 
PPTX
Dynamics
byShafie Sofian
 
PPTX
Introduction to Electrostatics
byNatasia Gouws
 
PPTX
Impulse
byRG Luis Vincent Gonzaga
 
PPTX
Terminal velocity pptx by Md Riad Badhon
byRiad Badhon
 
PPT
9 l pressure and moments
bycartlidge
 
PPTX
Physics: Waves
byJasmine Nikki Versoza
 
PPTX
IGCSE PHYSICS CORE: ATOMIC PHYSICS
byRozzie Jhana CamQue
 
Ch 9 Rotational Dynamics
byScott Thomas
 
Center Of Mass
byGillianWinters
 
Linear motion of a particle
byKhanSaif2
 
Displacement and Velocity
bymlong24
 
Electrostatics
bySeyid Kadher
 
Coulombs Law
bywilsonphysics
 
Electric Field & Electric Potential
byKC College
 
Momentum
bySells Middle School
 
Oscillations
byJulieber Bersabe
 
Conservation Laws
bySepti Pramuliawati
 
Magnetism and Electromagnetism
byShafie Sofian
 
Electric Fields
byChris Staines
 
1.1.1 gravitational fields
byJohnPaul Kennedy
 
Dynamics
byShafie Sofian
 
Introduction to Electrostatics
byNatasia Gouws
 
Impulse
byRG Luis Vincent Gonzaga
 
Terminal velocity pptx by Md Riad Badhon
byRiad Badhon
 
9 l pressure and moments
bycartlidge
 
Physics: Waves
byJasmine Nikki Versoza
 
IGCSE PHYSICS CORE: ATOMIC PHYSICS
byRozzie Jhana CamQue
 

Viewers also liked

PDF
Tahitian Noni International Spokespeople
byMorinda IPC
 
PPTX
Taking away the pain of leadership
byAlan Casey
 
PDF
Comparing Costs of an Electric Forklift versus Other Fuels
byForklift Trucks in Minnesota
 
PDF
How to express what you like in Spanish
bySpanishviaSkype
 
KEY
Da vinci style
bygrade5a
 
PPTX
The power of learning - for the real estate industry
byBetter Homes and Gardens Real Estate
 
PPTX
Pure Team Global - PURE Rank Advancements 2017 week 13
byCatherine Alicea
 
PDF
Taller de Innovación en valor - Metodo Blue Oean
byLetsmake Innovation & Fly!
 
PPT
#givingnames : asignación de DOI a tesis doctorales de @la_UPM / @biblioUPM
byBiblioteca UPM
 
PPSX
NETWORKING RELACIONAL: Nueva Dimensión y Perspectiva del Emprendimiento y los...
byNohelis RUIZ ARVELO Networking Strategist
 
PDF
Spanish Subjunctive - Practical Uses (B2)
bySpanishviaSkype
 
DOC
EL AYUNTAMIENTO DE MÁLAGA, REALIZÓ PAGOS POR VALOR DE 567 MILLONES DE EUROS E...
byAyuntamiento de Málaga
 
PPTX
The Saboteur in Your Retrospectives: How Your Brain Works Against You @ Indy....
byArthur Doler
 
PDF
Hot Potatoes TESL Ontario webinar March 2017
byJohn Allan
 
DOC
INFORMACIÓN DE MOVILIDAD PARA LOS PRÓXIMOS DÍAS
byAyuntamiento de Málaga
 
PDF
Boletín Informativo de abril 2017 da Biblioteca Sagrada Familia da Coruña
byBibliotecas Municipais de A Coruña
 
Tahitian Noni International Spokespeople
byMorinda IPC
 
Taking away the pain of leadership
byAlan Casey
 
Comparing Costs of an Electric Forklift versus Other Fuels
byForklift Trucks in Minnesota
 
How to express what you like in Spanish
bySpanishviaSkype
 
Da vinci style
bygrade5a
 
The power of learning - for the real estate industry
byBetter Homes and Gardens Real Estate
 
Pure Team Global - PURE Rank Advancements 2017 week 13
byCatherine Alicea
 
Taller de Innovación en valor - Metodo Blue Oean
byLetsmake Innovation & Fly!
 
#givingnames : asignación de DOI a tesis doctorales de @la_UPM / @biblioUPM
byBiblioteca UPM
 
NETWORKING RELACIONAL: Nueva Dimensión y Perspectiva del Emprendimiento y los...
byNohelis RUIZ ARVELO Networking Strategist
 
Spanish Subjunctive - Practical Uses (B2)
bySpanishviaSkype
 
EL AYUNTAMIENTO DE MÁLAGA, REALIZÓ PAGOS POR VALOR DE 567 MILLONES DE EUROS E...
byAyuntamiento de Málaga
 
The Saboteur in Your Retrospectives: How Your Brain Works Against You @ Indy....
byArthur Doler
 
Hot Potatoes TESL Ontario webinar March 2017
byJohn Allan
 
INFORMACIÓN DE MOVILIDAD PARA LOS PRÓXIMOS DÍAS
byAyuntamiento de Málaga
 
Boletín Informativo de abril 2017 da Biblioteca Sagrada Familia da Coruña
byBibliotecas Municipais de A Coruña
 

Similar to A Level Physics

PPT
Website impulse momentum
bystephm32
 
PPT
04-14-08 - Momentum And Impulse
bywjerlinger
 
PPTX
biomachanicsSports Sciences PPT.pptx
byVinodBaithaVinodSir
 
PPT
Power point slides for momentum, Impullse conservation of memntum
byKarthik537368
 
PPT
Chap9
byUniversity Malaysia Sabah
 
PPTX
Unit 5 A and B
byRachel Peak
 
PPT
7-ttmomentummmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm.ppt
bynivyasasheendran2
 
PPT
system of particles class 11 ncert book 1
byTJSingh28
 
PPTX
Momentum_and_Impulse SPP.pptx
byDharmsinh Desai of University
 
PPT
Conservation_of_Momentum_of class XII CBSE
byAtanuGhosh62
 
PPTX
grade 12 momentum.pptx
byElizerCuatonHimisola
 
PPT
P4 lesson part two
bysamuelaylward
 
PPTX
Newton's 2nd Law Of Motion explained in detail with relevant examples
byaarudhges
 
PPTX
Newton’s second law of motion
byDHRUVIL A ROCKSTAR
 
PPT
Momentum Intro
byJan Parker
 
PPTX
Science-9-Quarter-4-Week-3-tnygvj (1).pptx
byLourdesPalermo2
 
PDF
Momentum-and-Impulse-Powerpoint.pdf
byJoeMarieVelasquez1
 
PPT
Momentum.ppt
bykaren2747
 
PPTX
science9-momentumimpulseeeeeeeeeeeeeeeee
byryfreelance10
 
PDF
A2 PHYSICS - Notes.pdf
byLuisa Polanco
 
Website impulse momentum
bystephm32
 
04-14-08 - Momentum And Impulse
bywjerlinger
 
biomachanicsSports Sciences PPT.pptx
byVinodBaithaVinodSir
 
Power point slides for momentum, Impullse conservation of memntum
byKarthik537368
 
Chap9
byUniversity Malaysia Sabah
 
Unit 5 A and B
byRachel Peak
 
7-ttmomentummmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm.ppt
bynivyasasheendran2
 
system of particles class 11 ncert book 1
byTJSingh28
 
Momentum_and_Impulse SPP.pptx
byDharmsinh Desai of University
 
Conservation_of_Momentum_of class XII CBSE
byAtanuGhosh62
 
grade 12 momentum.pptx
byElizerCuatonHimisola
 
P4 lesson part two
bysamuelaylward
 
Newton's 2nd Law Of Motion explained in detail with relevant examples
byaarudhges
 
Newton’s second law of motion
byDHRUVIL A ROCKSTAR
 
Momentum Intro
byJan Parker
 
Science-9-Quarter-4-Week-3-tnygvj (1).pptx
byLourdesPalermo2
 
Momentum-and-Impulse-Powerpoint.pdf
byJoeMarieVelasquez1
 
Momentum.ppt
bykaren2747
 
science9-momentumimpulseeeeeeeeeeeeeeeee
byryfreelance10
 
A2 PHYSICS - Notes.pdf
byLuisa Polanco
 

Recently uploaded

PPTX
How to use search_read method in Odoo 18
byCeline George
 
PDF
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
PDF
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
PPTX
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 
PPTX
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
PPTX
Rectal Surgery in Senior Citiizens .pptx
byJohn Thanakumar
 
PDF
NAVIGATE PHARMACY CAREER OPPORTUNITIES.pdf
byMd. Zakaria Faruki
 
PDF
UKSG Forum 2025 - They asked for everything - The Case of the Systematic Revi...
byUKSG: connecting the knowledge community
 
PDF
Unit-III pdf (Basic listening Skill, Effective Writing Communication & Writin...
bySayyadTarannum
 
PDF
APM Wessex Network: DEIB Policy into Practice
byAssociation for Project Management
 
PDF
Projecte de la porta de primer B: L'antic Egipte
byeduardrubio1
 
PPTX
How to Manage Reception Report in Odoo 18 Inventory
byCeline George
 
PPTX
Semester 6 unit 2 Atopic dermatitis.pptx
bysachin7989
 
PDF
Digital Wellness in University Communities: Libraries as Guardians of Healthy...
bySylvester Ebhonu
 
PPTX
CHAPTER NO.08 HCP BY GG CLINICAL PHARMACY
byGanu Gavade
 
PDF
Projecte de la porta de la classe de primer A: Mar i cel.
byeduardrubio1
 
PPTX
Searching in PubMed andCochrane_Practical Presentation.pptx
bySystematic Reviews Network (SRN)
 
PPTX
The Art Pastor's Guide to the Liturgical Calendar
bySteve Thomason
 
DOCX
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 
PDF
Models of Teaching - TNTEU - B.Ed I Semester - Teaching and Learning - BD1TL ...
byDr Raja Mohammed T
 
How to use search_read method in Odoo 18
byCeline George
 
The Tale of Melon City poem ppt by Sahasra
bybitrasahasra
 
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
Rectal Surgery in Senior Citiizens .pptx
byJohn Thanakumar
 
NAVIGATE PHARMACY CAREER OPPORTUNITIES.pdf
byMd. Zakaria Faruki
 
UKSG Forum 2025 - They asked for everything - The Case of the Systematic Revi...
byUKSG: connecting the knowledge community
 
Unit-III pdf (Basic listening Skill, Effective Writing Communication & Writin...
bySayyadTarannum
 
APM Wessex Network: DEIB Policy into Practice
byAssociation for Project Management
 
Projecte de la porta de primer B: L'antic Egipte
byeduardrubio1
 
How to Manage Reception Report in Odoo 18 Inventory
byCeline George
 
Semester 6 unit 2 Atopic dermatitis.pptx
bysachin7989
 
Digital Wellness in University Communities: Libraries as Guardians of Healthy...
bySylvester Ebhonu
 
CHAPTER NO.08 HCP BY GG CLINICAL PHARMACY
byGanu Gavade
 
Projecte de la porta de la classe de primer A: Mar i cel.
byeduardrubio1
 
Searching in PubMed andCochrane_Practical Presentation.pptx
bySystematic Reviews Network (SRN)
 
The Art Pastor's Guide to the Liturgical Calendar
bySteve Thomason
 
Mobile applications Devlopment ReTest year 2025-2026
byDr. Mazin Mohamed alkathiri
 
Models of Teaching - TNTEU - B.Ed I Semester - Teaching and Learning - BD1TL ...
byDr Raja Mohammed T
 

A Level Physics

  • 1.
    3.6.1 Periodic motion 3.6.1.1Circular motion Review of Momentum 01/04/2017 09:05 141 1
  • 2.
    Momentum and itsconservation A review from AS work 01/04/2017 09:05 141 2
  • 3.
    Forces and acceleration Thiswill cause an acceleration in the direction of the stronger force. This can make an object slow down or speed up, or it can cause it to change direction. An object will remain stationary or will move in the same direction at a constant speed, unless the forces acting on it are not balanced. 01/04/2017 09:05 141 3
  • 4.
    Acceleration in acircle A motorbike drives round a corner at a constant speed. Its direction changes as it goes round the corner, so even though its speed is constant, it must be accelerating. This acceleration must be at right angles (perpendicular) to the direction of movement as it turns the corner, otherwise its speed could not be constant. Which way do you think the motorbike is accelerating, towards the inside of the bend, or away from it? 01/04/2017 09:05 141 4
  • 5.
    Force and accelerationare both vector quantities, unlike mass, so according to this equation, their directions must be equal. Forces causing circular motion m × aF = Any object that moves in a circle must be accelerating towards the centre of that circle. What causes this? What equation do you know that links force and acceleration? All circular motion must therefore be caused by a force acting towards the centre of the circle. This type of force is known as a centripetal force.01/04/2017 09:05 141 5
  • 6.
    Centrifugal force orcentripetal force? Swing a mass around in a circle on the end of a string. Do you feel a force pulling your hand outwards? This is often called a ‘centrifugal force’. You might have heard that centrifugal forces cause circular motion, but this is not good physics! The force on your hand is a reaction force, which can be ignored when studying the motion of the mass. Consider what is happening in this case. The mass on the end of the string is the object that is performing circular motion, so it is the forces on this object that are important: centripetal force 01/04/2017 09:05 141 6
  • 7.
    Thinking about circularmotion A washing machine dries clothes by spinning them round very fast: It is important to think of circular motion as an object being continuously prevented from moving in a straight line, rather than as if the object is being flung outwards from the centre. The sides of the drum provide the centripetal force that keeps the clothes moving in a circle, but water is free to escape in straight trajectories through the holes in the sides. 01/04/2017 09:05 141 7
  • 8.
    Momentum and itsconservation 01/04/2017 09:05 141 8
  • 9.
    Momentum and itsconservation 01/04/2017 09:05 141 9
  • 10.
    Symbol for momentumis p Unit: kg m s-1 Vector Momentum (p) is what ? Momentum (p) is the mass of an object multiplied by its velocity. momentum (p) = mass × velocity momentum (p) = mv When direction is not an important factor, how can we represent momentum? momentum = mass × speed Momentum 01/04/2017 09:05 141 10
  • 11.
    It is harderto stop a large truck than a small car when both are moving at the same speed. The truck has more momentum than the car. By momentum, we mean inertia in motion. Momentum 01/04/2017 09:05 141 11
  • 12.
  • 13.
    • A movingtruck has more momentum than a car moving at the same speed because the truck has more mass. • A fast car can have more momentum than a slow truck. • A truck at rest has no momentum at all. • Next: A truck rolling down a hill Momentum 01/04/2017 09:05 141 13
  • 14.
    A truck rollingdown a hill has more momentum than a roller skate with the same speed. But if the truck is at rest and the roller skate moves, then the skate has more momentum. Momentum 01/04/2017 09:05 141 14
  • 15.
    Can you thinkof a case where a roller skate and a truck would have the same momentum? Momentum Answer: The roller skate and truck can have the same momentum if the speed of the roller skate is much greater than the speed of the truck. For example, a 1000-kg truck backing out of a driveway at 0.01 ms-1 has the same momentum as a 1-kg skate going 10 ms-1. Both have momentum = 10 kg ms-1. 01/04/2017 09:05 141 15
  • 16.
    When objects collide,assuming that there are no external forces, then momentum is always conserved.... Definition : When two or more objects interact, the total momentum remains constant provided that there is no external resultant force Conservation of Momentum 1 Mass 75 kg Velocity 4 ms-1 Mass 50 kg Velocity 0 ms-1 Mass 125 kg Velocity ??? ms-1 Mass 125 kg Velocity 2.4 ms-1 01/04/2017 09:05 141 16
  • 17.
    Conservation of Momentum1 01/04/2017 09:05 141 17
  • 18.
    The force orimpulse that changes momentum must be exerted on the object by something outside the object. • Molecular forces within a football have no effect on the momentum of the football. • A push against the dashboard from inside does not affect the momentum of a car. These are internal forces. They come in balanced pairs that cancel within the object. Conservation of Momentum 01/04/2017 09:05 141 18
  • 19.
    Which is moreeffective at demolishing a wall? A 1kg metal ball moving at 50ms-1 Or a 1000kg ball moving at 1ms-1 Momentum 01/04/2017 09:05 141 19
  • 20.
    Which is moreeffective at demolishing a wall? 1kg x 50ms-1 = 50 kg.ms-1 1000kg x 1ms-1= 1000 kg.ms-1 Momentum  01/04/2017 09:05 141 20
  • 21.
  • 22.
    Linear Momentum Change inmomentum: (a) mv (b) 2mv 01/04/2017 09:05 141 22
  • 23.
    Momentum The momentum ofan object: depends on what? Depends on the object’s mass. Momentum is directly proportional to what ? Momentum is directly proportional to mass. What does the object’s movement depend on ? Depends on the object’s velocity. Momentum is directly proportional to what ? Momentum is directly proportional to velocity. 01/04/2017 09:05 141 23
  • 24.
    Momentum • In symbols: p= mv p m v 01/04/2017 09:05 141 24
  • 25.
    Example 1 A cowof mass 640kg charges after a man at 7m s-1 to steal his crisps. What is the momentum of the cow? Write down the physics P = mv Using standard notation: m = 640kg v = 7m s-1 p = mv = 640 x 7 = 4 480 kg m s-1 01/04/2017 09:05 141 25
  • 26.
    Example 2 Highly-trained assassinhamsters in the Amazon rainforest can run at a top speed of 62.22 m s-1 (140 mph). One such hamster has a momentum of 156 kg m s-1. What is the mass of the hamster? Using standard notation: v = 62.22 m s-1 p = 156 kg m s-1 p = mv m = p / v = 156 / 62.22 = 2.5 kg One hefty hamster! Write down the physics P = mv 01/04/2017 09:05 141 26
  • 27.
    How do weend up with F = ma ? N2 says that the rate of change of momentum is proportional to the force OR force is proportional to the change of momentum per second. So, consider an object of mass, m, with a force, F, on it. It will accelerate from velocity u to velocity v. Initial momentum = mu. Final momentum = mv. Δp = mv – mu According to N2, F is proportional to Δp per second.  F    BUT a = (v-u) / t  F  ma OR F = kma If we define the newton as the force required to accelerate 1 kg by 1 m s-2, we get: F = ma Δp time taken mv - mu t m (v – u) t 01/04/2017 09:05 141 27
  • 28.
    Using Newton’s SecondLaw You would generally give Newton’s second law as: F = If mass remains constant: F = OR F = ma If mass is changing: F = where Δm / Δt is the mass change per second Δ (mv) Δt m Δv Δt v Δm Δt 01/04/2017 09:05 141 28
  • 29.
    Worked example Our 2.5kgpsychopathic hamster Amazonian assassin. He is cruising along at 60 m s-1 when he approaches his victim. He uses his super fur-brakes to apply a braking force of 12N. How long does it take until the hamster has stopped? Using standard notation: m = 2.5kg Δv = 60 m s-1 F = 12N Newton 2: F = m Δv / Δt Δt = m Δv / F = 2.5 x 60 / 12 = 12.5s 01/04/2017 09:05 141 29
  • 30.
    The hamster attacksits prey by firing 3kg of acid in 2s at the poor animal. It doesn’t stand a chance. But the hamster has to hang on tightly to a tree because it is pushed backwards by the force needed to fire its deadly liquid. If the hamster is able to hold on with a maximum grip of 30N, how fast can he fire his acid? Using standard notation: F = 30N Δm = 3kg Δt = 2s Newton 2: F = v Δm / Δt v = F Δt / Δm = 30 x 2 / 3 = 20 ms-1 01/04/2017 09:05 141 30
  • 31.
    Impulse and ImpactForces 01/04/2017 09:05 141 31
  • 32.
    The longer aforce acts on an object, the greater its effect. Air rifles can fire much further than air pistols (partly) because the barrels are longer. Pistol Rifle 01/04/2017 09:05 141 32
  • 33.
    Impulse = FΔt = Δ (mv) impulse = what changes ? impulse = change of momentum Unit usually given as ? Unit usually given as N s - but could be given as ? Unit usually given as N s - but could be given as kg m s-1 01/04/2017 09:05 141 33
  • 34.
    Worked example A tennisball of mass 0.20kg moving at a speed of 18ms-1 was hit by a bat, causing the ball to go back in the direction it came from at a speed of 15ms-1. The contact time was 0.12s. Calculate: a the change of momentum of the ball; b the impact force on the ball. Using standard notation: m = 0.20kg u = 18ms-1 v = -15ms-1 a change of momentum = m(v-u) = 0.20 (-15-18) = -6.6kgms-1 b F = change of momentum / time taken = -6.6 / 0.12 = -55N 01/04/2017 09:05 141 34
  • 35.
    Force-time graphs (seenotes) If a force acts on an object for a certain time, the object’s momentum will change. We can draw a force-time graph for the object. E.g. During take-off, an aeroplane’s engines exert a force of 5kN for 20s. Force Time What can you tell from the graph? The area under a force-time graph tells you the impulse (or change in momentum). 01/04/2017 09:05 141 35
  • 36.
    Impact Forces (seenotes) An impact force changes the momentum of an object. The force is given by: F = mv - mu t 01/04/2017 09:05 141 36
  • 37.
    Worked example A ballof mass 0.63kg, initially at rest, was struck by a bat which gave it a velocity of 35ms-1. The contact time between the bat and the ball was 25ms. Calculate: a the momentum gained by the ball; b the average force of impact on the ball. Using standard notation: m = 0.63kg v = 35ms-1 t = 0.025s a p = mv = 0.63 x 35 = 22kgms-1 b Using impulse: Ft = Δmv F = Δmv / t = 22 / 0.025 = 880N 01/04/2017 09:05 141 37
  • 38.
    If an objecthits a wall at an angle, you only need to consider the components of velocity in the direction of the force.   u cos  v cos  When an object rebounds after impact, be very careful with directions of F, m and v. A couple of points to bear in mind 01/04/2017 09:05 141 38
  • 39.
    Impulse • The impulseexerted on an object depends on: • The force acting on the object. • Impulse is directly proportional to force. • The time that the force acts. • Impulse is directly proportional to time. 01/04/2017 09:05 141 39
  • 40.
    Definition : The impulseof a force is defined as the product of the force and the time which the force acts for The impulse = Ft = mv The impulse of the force acting upon an object is equal to the change of momentum for the force Impulse of a Force 01/04/2017 09:05 141 40
  • 41.
    Impulse • In symbols: I= Ft I F t 01/04/2017 09:05 141 41
  • 42.
  • 43.
    Collisions – Example1 •Collisions may be the result of direct contact. •The impulsive forces may vary in time in complicated ways. • This force is internal to the system. • Observe the variations in the active figure. •Momentum is conserved. 01/04/2017 09:05 141 43
  • 44.
    Collisions – Example2 •The collision need not include physical contact between the objects. •There are still forces between the particles. •This type of collision can be analysed in the same way as those that include physical contact. 01/04/2017 09:05 141 44
  • 45.
    Impulse Therefore, the same changein momentum may be produced by a large force acting for a short time, or by a smaller force acting for a longer time. 01/04/2017 09:05 141 45
  • 46.
    Impulse Impulse is awhat type of quantity? Impulse is a vector quantity. Common units of impulse are ? Common units of impulse: N s 01/04/2017 09:05 141 46
  • 47.
    When a dishfalls, will the impulse be less if it lands on a carpet than if it lands on a hard floor? True or false ? Impulse Changes Momentum Answer: False. The impulse would be the same for either surface because the same momentum change occurs for each. It is the force that is less for the impulse on the carpet because of the greater time of momentum change. 01/04/2017 09:05 141 47
  • 48.
    Impulse & Momentum Theimpulse exerted on an object equals the object’s what? (in terms of momentum) ? The impulse exerted on an object equals the object’s change in momentum 01/04/2017 09:05 141 48
  • 49.
  • 50.
    Impulse & Momentum •In symbols: I = p 01/04/2017 09:05 141 50
  • 51.
    Impulse-Momentum: Crash TestExample •Conceptualize • The collision time is short. • We can image the car being brought to rest very rapidly and then moving back in the opposite direction with a reduced speed. •Categorise • Assume net force exerted on the car by wall and friction with the ground is large compared with other forces. • Gravitational and normal forces are perpendicular and so do not effect the horizontal momentum. 01/04/2017 09:05 141 51
  • 52.
    Impulse physics problemsolved 01/04/2017 09:05 141 52
  • 53.
    Collisions and Explosions Objective •Be able to apply the principle of conservation of momentum to explosions and collisions. 01/04/2017 09:05 141 53
  • 54.
    Conservation of Momentum Considerseveral objects which interact with each other. If there is no external force, tells us that there will be no change in momentum. BUT momentum can be transferred between the objects. When doing problems involving collisions or explosions, just work out the momentum at the start and equate it with the momentum at the end. Principle of conservation of momentum: for a system of interacting objects, the total momentum remains constant, provided no external resultant force acts on the system. In English, this means: total momentum before = total momentum after 01/04/2017 09:05 141 54
  • 55.
    Worked example A sheepof mass 100kg is out for a run one day. He picks up speed until he reaches 8ms-1, when he runs into a stationary shopping trolley of mass 20kg. The force of the impact slows our sheep to 6ms-1, and causes the trolley to start moving. What is the velocity of the trolley immediately after impact? Using standard notation: Sheep: ms = 100kg us = 8ms-1 vs = 6ms-1 Trolley: mt = 20kg ut = 0ms-1 Total initial momentum = initial momentum of sheep + initial momentum of trolley = (100 x 8) + (20 x 0) = 800kgms-1 Total final momentum = final momentum of sheep + final momentum of trolley = (100 x 6) + (20 x vt) = 600 + 20vt Using principle of conservation of momentum: 800 = 600 + 20vt vt = 10ms-1 01/04/2017 09:05 141 55
  • 56.
  • 57.
    Three types ofcollision: Elastic No kinetic energy is lost in the collision (dropped ball rebounds to original height) Totally inelastic The objects stick together (railway wagons) Partially elastic The objects move apart but have less kinetic energy than before (cars colliding) Reminder: KE = ½ mv2 Remember: Momentum is ALWAYS conserved in a collision. KE may be converted to other forms of energy. Where does all the KE disappear to? 01/04/2017 09:05 141 57
  • 58.
    Worked example Buzz Lightyearhas a mass of 160kg in his space suit. He flies straight at Zurg at 40ms-1. Zurg is a baddie so, although he has 20kg more mass that Buzz, he can only fly at 30ms-1, and he is doing this – straight towards Buzz! Assuming they stick together in one tousling lump, calculate: a the speed and direction of Buzz and Zurg immediately after impact; b the loss of kinetic energy due to the impact. Using standard notation: mB = 160kg uB = 40ms-1 mZ = 180kg uZ = - 30ms-1 a Initial momentum = (160 x 40) - (180 x 30) = 1000kgms-1 Final momentum = (160 + 180) v Using principle of conservation of momentum: 1000 = 340v v = 2.94ms-1 in the direction in which Buzz was initially travelling. b KE before impact = (0.5 x 160 x 40 x 40) + (0.5 x 180 x -30 x -30) = 209kJ KE after impact = (0.5 x 340 x 2.94 x 2.94) = 1.5kJ Loss of KE = 207.5kJ 01/04/2017 09:05 141 58
  • 59.
  • 60.
  • 61.
    Angles can bemeasured in both degrees & radians : Radians & Degrees The angle  in radians is defined as the arc length / the radius For a whole circle, (360°) the arc length is the circumference, (2r)  360° is 2 radians  Arc length r Common values : 45° = /4 radians 90° = /2 radians 180° =  radians Note. In S.I. Units we use “rad” 01/04/2017 09:05 141 61
  • 62.
    Angular velocity, forcircular motion, has counterparts which can be compared with linear speed s=d/t. Time (t) remains unchanged, but linear distance (d) is replaced with angular displacement  measured in radians. Angular Displacement  Angular displacement  r r Angular displacement is the number of radians moved 01/04/2017 09:05 141 62
  • 63.
    Consider a bikewheel which is rotating. In order to do useful calculations, we need to talk about angular displacement and angular velocity.  = angular displacement (rad) = angular velocity (rad s-1) If the wheel takes T seconds to rotate once, it will turn through an angle of 2 / T radians each second. The frequency of rotation will be given by f = 1/T The angular displacement in a certain amount of time, t, is given by:  = 2t / T OR  = 2ft Angular Displacement 01/04/2017 09:05 141 63
  • 64.
    Consider an objectmoving along the arc of a circle from A to P at a constant speed for time t: Angular Velocity : Definition Definition : The rate of change of angular displacement with time “The angle, (in radians) an object rotates through per second”  =  / t  Arc length r r P A This is all very comparable with normal linear speed, (or velocity) where we talk about distance/time Where  is the angle turned through in radians, (rad), yields units for  of rads-1 01/04/2017 09:05 141 64
  • 65.
    Circumference = 2r Timefor one rotation = distance travelled / velocity = 2r / v OR 2 /  In other words: 2r / v = 2 /  v = r  Angular Velocity From the previous slide,  = 2ft We also know that  =  / t   = 2f 01/04/2017 09:05 141 65
  • 66.
    Worked example A cyclisttravels at a speed of 12 ms-1 on a bike which has wheels of radius 40cm. Calculate: a the frequency of rotation of each wheel; b the angular speed of each wheel; c the angle the wheel turn through in 0.10s in: i radians ii degrees Using standard notation: v = 12ms-1 r = 0.4m a circumference = 2 x  x 0.4 = 2.5m T = circumference / speed = 2.5 / 12 = 0.21s f = 1 / T = 1 / 0.21 = 4.8Hz b  = 2f = 30rads-1 c i  = t = 30 x 0.1 3.0rad ii  = 3.0 x 360 / 2 = 1720 01/04/2017 09:05 141 66
  • 67.
    The period Tof the rotational motion is the time taken for one complete revolution (2 radians). Angular Velocity : Period & Frequency Substituting into :  =  / t (angular speed) f = 1/T and  = 2f (see notes) Substituting for f :  = 2 / T T = 2 /  From our earlier work on waves we know that the period (T) & frequency (f) are related T = 1/f f =  / 2 01/04/2017 09:05 141 67
  • 68.
    Considering the diagrambelow, we can see that the linear distance travelled is the arc length Angular Velocity : linear speed Linear speed (v) = arc length (AP) / t v = r / t Substituting... ( =  / t) v = r  Arc length r r P A 01/04/2017 09:05 141 68
  • 69.
    A cyclist travelsat a speed of 12ms-1 on a bike with wheels which have a radius of 40cm. Calculate: a. The frequency of rotation for the wheels b. The angular velocity for the wheels c. The angle the wheel turns through in 0.1s in i radians ii degrees Angular Velocity : Worked example 01/04/2017 09:05 141 69
  • 70.
    The frequency ofrotation for the wheels Circumference of the wheel is = = 2r (subs for r) = = 2 x 0.4m = 2.5m Time for one rotation, (the period s) is found using: ? s =d / t …. rearranged for t t = d / s = T = circumference / linear speed or T= T = 2.5 / 12 = 0.21s  f = f = 1 / T = 1 / 0.21 = 4.8Hz Angular Velocity : Worked example 01/04/2017 09:05 141 70
  • 71.
    The angular velocityfor the wheels Using T = 2 / , rearranged for   = 2 / T … subs for T  = 2 / 0.21 = ?  = 30 rads-1 Angular Velocity : Worked example 01/04/2017 09:05 141 71
  • 72.
    The angle thewheel turns through in 0.1s in i radians ii degrees Using  =  / t re-arranged for   = t … subs for  and t  = 30 x 0.1 = ?  = 3 rad …. In degrees? = 3 x (360°/ 2) = 172° Angular Velocity : Worked example 01/04/2017 09:05 141 72
  • 73.
  • 74.
    Centripetal Force If youpick any point on this bike wheel, it will rotate with a constant speed, but its direction will be constantly changing. This means its velocity is changing. It is always accelerating. This is called centripetal acceleration. Centripetal acceleration is given by: a = v2 / r = 2 r And, since it’s accelerating, there must be a force. This is called centripetal force. By applying N2, we get: F = mv2 / r = mr2 01/04/2017 09:05 141 74
  • 75.
    Worked example A stoneof mass 0.5kg is swung round in a horizontal circle (on a frictionless surface) of radius 0.75m with a steady speed of. Calculate: a the centripetal acceleration of the stone; b the centripetal force acting on the stone. Using standard notation: m= 0.5kg r= 0.75m v= 4ms-1 a) a = v2/r = 42 / 0.75 = 21.4 m s-2 b) F = ma = 0.5 x 21.4 = 10.7 N Notice that this is a linear acceleration and not an angular acceleration. The angular velocity of the stone is constant and so there is no angular acceleration.01/04/2017 09:05 141 75
  • 76.
    Applications of CircularMotion - Cars Objective • Explain what forces are experienced when cars travel over hills and round bends. 01/04/2017 09:05 141 76
  • 77.
    Cars going overbumps / hills / bridges S mg v The car is supported by a force, S. When v=0, S = mg. As v increases, the car has a greater tendency to continue in a straight line. This is because S decreases. The centripetal force is the resultant of S and mg: F = mg - S And we know that F = mv2 / r  mg – S = mv2 / r As v increases, a greater centripetal force is required to keep it moving in a circle. This happens by S decreasing. Fmax occurs when S = 0 The fastest speed the car can travel over the hill will be given by: mg = mvmax 2 / r OR vmax = gr 01/04/2017 09:05 141 77
  • 78.
    Cars going roundbends v Friction The centripetal force is provided by the friction of the tyres on the road. The car has a certain top speed, vmax before it begins to slip on the road because the friction is not enough to provide the centripetal force. Frictionmax = m vmax 2 / r In questions on this sort of thing, you’ll be given details of the friction. 01/04/2017 09:05 141 78
  • 79.
    Banked tracks This issupposed to be a car coming towards us. It’s travelling round a bend and the track is banked at an angle, . mg  R Centripetal force IF there’s no friction on the tyres, the centripetal force is provided by the horizontal component of R. F = R sin (which is also equal to mv2 / r) mg is balanced by the vertical component of R, so: mg = R cos R sin R cos = mv2 rmg OR tan = v2 / gr 01/04/2017 09:05 141 79
  • 80.
    My hamster hasa mass of 2kg (he’s a big lad). He has a top speed of 15ms-1. Is he able to run over a hill of radius 20m at top speed without taking off? (g = 9.8ms-2). Worked example Say the hamster is supported by a force, S. The centripetal force is the resultant of S and mg: F = mg – S Fmax will occur when S = 0 Fmax = mg BUT centripetal force is also given by F = mv2 / r The fastest the animal can travel over the hill will be given by: mg = mvmax 2 / r vmax = gr = 14ms-1 No, he can’t run over the hill at top speed. 01/04/2017 09:05 141 80
  • 81.
    Centripetal acceleration &Force 01/04/2017 09:05 141 81
  • 82.
    Centripetal acceleration &Force 01/04/2017 09:05 141 82
  • 83.
    If an objectis moving in a circle with a constant speed, it’s velocity is constantly changing.... Because? Because the direction is constantly changing.... If the velocity is constantly changing then by definition the object is accelerating – what about force? If the object is accelerating, then an unbalanced force must exist Centripetal Acceleration : Introduction Velocity v 01/04/2017 09:05 141 83
  • 84.
    Centripetal Acceleration :Proof 1 Velocity vB  Velocity vA Consider an object moving in circular motion with a speed v which moves from point A to point B in t seconds (From speed=distance / time), the distance moved along the arc AB, s is? vt Velocity vB Velocity vA v C A B  The vector diagram shows the change in velocity v : (vB – vA)01/04/2017 09:05 141 84
  • 85.
    Centripetal Acceleration :Proof 2 Velocity vB  Velocity vA The triangles ABC & the vector diagram are similar If  is small, then v / v = s / r Velocity vB Velocity vA v C A B  Substituting for s = vt v / v = vt / r (a = change in velocity / time) a = v / t = v2 / r 01/04/2017 09:05 141 85
  • 86.
    Applications of CircularMotion – Fairground Rides 01/04/2017 09:05 141 86
  • 87.
    Big dippers When yougo down a dip, you’re forced down into your seat. The centripetal force is the resultant of S and mg, and is also equal to mv2 / r: F = S – mg = mv2 / r  S = mg + mv2 / r S represents the support force of the track on the car. Since we experience mg in normal circumstances anyway, the extra force pushing downwards is mv2 / r 01/04/2017 09:05 141 87
  • 88.
    L mg S Very long swings Maximumspeed is calculated by equating GPE at the top and KE at the bottom: v2 = 2gh At the lowest point, centripetal force is provided by the resultant of S and mg: S – mg = mv2 / L BUT v2 = 2gh S – mg = 2mgh / L OR S = mg + 2mgh / L Since we experience mg in normal circumstances anyway, the extra force experienced is 2mgh / L 01/04/2017 09:05 141 88
  • 89.
    Person at top R +mg Big wheel thingy On this big wheel thingy, the riders are being squished against the inside of the circumference. At the maximum height, the centripetal Force is provided by R + mg and is equal to mv2 / r R = mv2 / r - mg R is the reaction force from the wheel. At a certain speed, v0 (so that v0 2 = gr), R = 0.  There is no reaction force on the person. You must have a minimum speed of v0 to stop people falling out. 01/04/2017 09:05 141 89
  • 90.
    Examples of centripetalforces More examples of circular motion caused by centripetal forces: Can you work out the direction of the force in each case, and describe the type of force involved? 01/04/2017 09:05 141 90
  • 91.
    How does thecentripetal force depend on mass? F = ma, so force is proportional to acceleration. If the truck is going faster, or if its radius is smaller, then it is changing direction more quickly, so its acceleration is greater. How does the centripetal force depend on speed and radius? F = ma, so force is proportional to mass. The greater the mass, the larger the centripetal force needed to maintain circular motion. The greater the speed, and the smaller the radius, the larger the centripetal force needed to maintain circular motion. Factors affecting centripetal forces 01/04/2017 09:05 141 91
  • 92.
  • 93.
  • 94.
    Centripetal Acceleration :angular We can substitute for angular velocity.... a = v2 / r We have already seen that: v = r (substituting for v into above) a = (r)2 / r or a = a = r2 01/04/2017 09:05 141 94
  • 95.
    Centripetal Force In exactlythe same way as we can connect force f and acceleration a using Newton’s 2nd law of motion, we can arrive at the centripetal force which is keeping the object moving in a circle f = mv2 / r or f = mr2 Any object moving in a circle is acted upon by a single resultant force towards the centre of the circle. We call this the centripetal force01/04/2017 09:05 141 95
  • 96.
    Centripetal Force :CentripetalForce : Using this stuff!Centripetal Force : Gravity & Orbits 01/04/2017 09:05 141 96
  • 97.
    Centripetal Force :Gravity & Orbits Gravity which keeps satellites in orbit around Earth and the Earth in orbit around the sun is a classic example of a centripetal force. Planet satellite Gravity 01/04/2017 09:05 141 97
  • 98.
    The wheel ofthe London Eye has a diameter of 130m and takes 30mins for 1 revolution. Calculate: a. The speed of the capsule b. The centripetal acceleration c. The centripetal force on a person with a mass of 65kg Worked example 1 01/04/2017 09:05 141 98
  • 99.
    The speed ofthe capsule : Using v = r we know that we do a full revolution (2 rad) in ? 30mins (1800s) v = = (130/2) x (2 / 1800) … v = v = 0.23 ms-1 Worked example 1 01/04/2017 09:05 141 99
  • 100.
    The centripetal acceleration: Usinga = v2 / r a = (0.23)2 / (130/2) a = 7.92 x 10-4 ms-2 The centripetal force: (equation?) Using f = ma F = 65 x 7.92 x 10-4 F = 0.051 N Worked example 1 01/04/2017 09:05 141 100
  • 101.
    Centripetal Force &the Road 01/04/2017 09:05 141 101
  • 102.
    Centripetal Force &the Road 01/04/2017 09:05 141 102
  • 103.
    An object movingin a circle has a constantly changing velocity, it is therefore experiencing acceleration and hence a force towards the centre of rotation. What do we call this force? We called this the centripetal force: The force required to keep the object moving in a circle. In reality this force is provided by another force, e.g. The tension in a string, friction or the force of gravity. Centripetal Acceleration : Recap 01/04/2017 09:05 141 103
  • 104.
    Consider a carwith mass m and speed v moving over the top of a hill... Over the top 1 mg r S 01/04/2017 09:05 141 104
  • 105.
    At the topof the hill, the support force S, is in the opposite direction to the weight (mg). It is the resultant between these two forces which keep the car moving in a circle mg – S = mv2 / r If the speed of the car increases, there will eventually be a speed v0 where the car will leave the ground (the support force S is 0) mg = mv0 2 / r v0 = (gr)½ Any faster and the car will leave the ground Over the top 2 01/04/2017 09:05 141 105
  • 106.
    On a levelroad, when a car travels around a roundabout the centripetal force required to keep the car moving in a circle is provided by the friction between the road surface and tyres Around a Roundabout 1 velocity friction Force of Friction F F = mv2 / r 01/04/2017 09:05 141 106
  • 107.
    Factors affecting centripetalforces 01/04/2017 09:05 141 107
  • 108.
    To avoid skiddingor slipping, the force of friction F0 must be less than the point where friction is overcome which occurs at speed v0 Friction is proportional to weight and can be given by the coefficient of friction (): F  mg F = mg At the point of slipping: F0 = mv0 2 / r  mg = mv0 2 / r  v0 = (gr)½ Around a Roundabout 2 01/04/2017 09:05 141 108
  • 109.
    For high speedtravel, race tracks etc have banked corners. In this way a component of the car’s weight is helping friction keep the car moving in a circle Banked Tracks 1 mg N1 N2    Towards centre of rotation 01/04/2017 09:05 141 109
  • 110.
    Without any bankingthe centripetal force is provided by friction alone. Banked corners allows greater speeds before friction is overcome The centripetal force is provided by the horizontal components of the support forces (N1 + N2) sin  = mv2 / r and the vertical components balance the weight (N1 + N2) cos  = mg Banked Tracks 2 01/04/2017 09:05 141 110
  • 111.
    Rearranging sin  =mv2 / (N1 + N2) r cos  = mg / (N1 + N2) and since tan  = sin  / cos  tan  = mv2 / (N1 + N2) r x (N1 + N2) / mg tan  = mv2 / mgr v2 = gr tan  Thus there is no sideways frictional force if the speed v is such that v2 = gr tan  Banked Tracks 3 01/04/2017 09:05 141 111
  • 112.
    Centripetal Force &the Fairground 01/04/2017 09:05 141 112
  • 113.
    Centripetal Force &the Fairground 01/04/2017 09:05 141 113
  • 114.
    At the bottomof a big dipper you are pushed into your seat and feel “heavier”... Centripetal Force: Big Dippers 1 Centre of curvature mg velocity 01/04/2017 09:05 141 114
  • 115.
    At the bottomof the dip at speed v with radius r, Resolving the vertical forces: S – mg = mv2 / r S = mg + mv2 / r The “extra” weight you experience when feeling “heavy” is given by the centripetal force Centripetal Force: Big Dippers 2 01/04/2017 09:05 141 115
  • 116.
    Consider a personof mass m on a very long swing of length r Centripetal Force: The Long Swing 1 Fixed point To winch Initial position r S mg Velocity 01/04/2017 09:05 141 116
  • 117.
    As the swingis released we can consider the conservation of energy, loss in potential energy is the gain in the kinetic energy mgh = ½mv2  v2 = 2gh The passenger is on a circular path with radius r. At the bottom of the swing the support force S acts against the person’s weight mg. This provides the centripetal force: S – mg = mv2/r Centripetal Force: The Long Swing 2 01/04/2017 09:05 141 117
  • 118.
    Substituting for v2: S– mg = mv2/r S – mg = 2mgh/r S = mg + 2mgh/r The person “feels heavier” by 2mgh/r, if the swing drops through 90°, then the extra support force is twice the persons weight (mg) Centripetal Force: The Long Swing 3 01/04/2017 09:05 141 118
  • 119.
    Consider a fairgroundride which spins fast enough to keep you in place even when upside down at the top of the ride.... Centripetal Force: The wall of death 1 Velocity Rotation Reaction R & weight mg 01/04/2017 09:05 141 119
  • 120.
    The wheel turnsfast enough to keep the passenger in position as they pass over the top. At the top, the reaction R acts downwards and together with the weight provides the centripetal force: mg + R = mv2/ r R = mv2/ r – mg At a certain speed v0 such that v0 2 = gr, then the reaction from the wall will be zero Centripetal Force: The wall of death 2 01/04/2017 09:05 141 120
  • 121.
    What is gravity? Ifa skydiver steps out of a plane, which way does he move? What causes this effect? Gravity is a universal force which attracts any mass to every other mass in the Universe. Every mass has its own gravitational field, like the one surrounding Earth, but it takes two objects to make a gravitational force. Gravity is a very weak force, so small objects don’t stick together, but if at least one mass is very large, the effect of gravity is easy to see. Skydivers always fall back to Earth!01/04/2017 09:05 141 121
  • 122.
    Factors affecting gravity Thebigger the mass, the stronger its gravitational field, so the Sun has a much stronger gravitational field than Earth. Gravitational fields are stronger:  around larger masses  at shorter distances. The gravitational force between two objects can be increased:  by increasing the size of either or both of the masses  by decreasing the distance between them. But the further apart two objects are, the weaker the gravitational forces between them. So when a skydiver jumps out of a plane, he falls to Earth, not towards the Sun! 01/04/2017 09:05 141 122
  • 123.
    Gravitational chaos! Every massin the universe attracts every other. That’s a lot of forces to keep track of! But gravity is a very weak force, so most gravitational forces at the Earth’s surface can be ignored. The gravitational field of a pen, a person or even a large mountain is too weak to have a noticeable effect, so the only gravitational field you need to consider is Earth’s. 01/04/2017 09:05 141 123
  • 124.
    Gravity at theEarth’s surface Gravitational fields get weaker with increasing distance. Do you feel any lighter on the top floor of your house than on the ground floor? The Earth is so large that small changes in height don’t affect weight, so gravitational field strength is effectively constant: weight = mass × gravitational field strength This applies to objects at the Earth’s surface, at the top of a mountain, or even in an aeroplane at 30000 feet… …but be careful! This does not apply to satellites in orbit, or to the forces between planets and stars. = mass × 10 N/kg 01/04/2017 09:05 141 124
  • 125.
  • 126.
    Gravity as acentripetal force Examples of centripetal forces can be found in many everyday contexts, but what about circular motion on a large scale? What is the centripetal force that makes orbits possible? Unlike a mass on a string, stars and planets are not physically connected to each other, but they are attracted to each other by gravity. How does circular motion under gravity compare to the types of circular motion we are used to? 01/04/2017 09:05 141 126
  • 127.
    Circular motion undergravity The centripetal force required to keep a planet in circular motion depends on mass, radius and speed. But the gravitational force that a star actually provides only depends on mass and radius. This means that for any specific radius, a planet must move at one specific speed to stay in orbit.  When a mass on a string is swung at an increasing speed, the tension increases, while the radius remains constant:  If a planet orbits a star at an increasing speed, the force between them does not increase, so it moves out of that orbit: 01/04/2017 09:05 141 127
  • 128.
    Circular motion undergravity 01/04/2017 09:05 141 128
  • 129.
    Elliptical orbits In 1605Johannes Kepler used his observations of the orbit of Mars to predict that, rather than moving in perfectly circular orbits, all the planets follow elliptical orbits around the Sun: Each orbit forms an ellipse with the Sun at one focus. The two focuses of an ellipse are similar to the single centre of a circle. focus 01/04/2017 09:05 141 129
  • 130.
    The head ofthe comet is a lump of ice and dust a few kilometres across. The tail only appears when the comet is near the Sun. It consists of gas and dust which are released by the heat of the Sun. Comets Most of the planets travel around the Sun in near-circular orbits. Comets also travel around the Sun but in highly elliptical orbits. gas tail dust tail 01/04/2017 09:05 141 130
  • 131.
  • 132.
    What is asatellite? A satellite is an object that orbits a planet. Satellites can be natural or they can be artificial. The same physics applies to satellites orbiting the Earth as to planets orbiting the Sun. The largest satellite orbiting Earth is the Moon. This is Earth’s only natural satellite. Artificial satellites are put into orbit for a range of purposes, such as mapping and surveillance. 01/04/2017 09:05 141 132
  • 133.
  • 134.
    Uses for geostationarysatellites Geostationary satellites are particularly useful because they stay fixed above a single point on Earth. This makes them useful for communications and satellite TV broadcasting, because the satellite never goes out of range. Geostationary satellites are also used for weather forecasting. Satellite dishes can be fixed to face in the correct direction, without the need to track the movement of the satellite. 01/04/2017 09:05 141 134
  • 135.
    Problems with geostationarysatellites There are some disadvantages to geostationary satellites.  All geostationary satellites must orbit over the equator at a specific altitude of 36000km. There are limited slots in this orbit, which can lead to disputes when different countries want a certain slot.  A geostationary satellite can only ‘see’ a certain area of the Earth’s surface – the rest is hidden from view.  All geostationary satellites are a long way from Earth, which causes delays in signals. This can be a disadvantage during commercial or military communications.01/04/2017 09:05 141 135
  • 136.
    Uses for polarorbit satellites Polar satellites are particularly useful because they orbit at a low altitude and high speed. This makes them useful for mapping, as they can image the Earth’s surface in higher resolution than more distant satellites. It also makes them useful for observation purposes, such as military surveillance, or weather monitoring, as they can view the whole of the Earth’s surface in one day. However, polar satellites must be tracked from the ground, and will be out of range for much of the time, causing delays in data retrieval.01/04/2017 09:05 141 136
  • 137.
    Which type ofsatellite? 01/04/2017 09:05 141 137
  • 138.
  • 139.
  • 140.
  • 141.