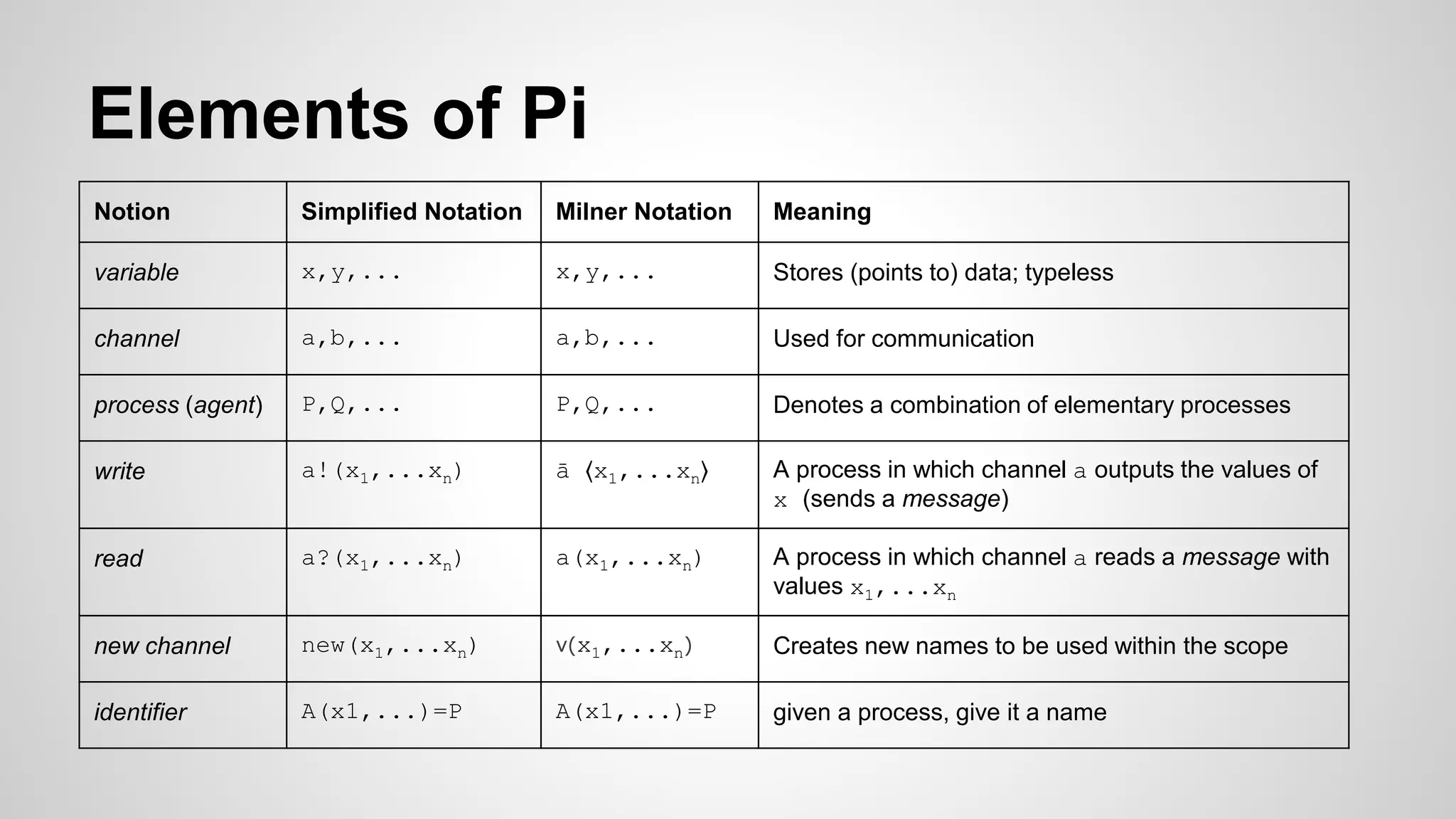
The document discusses the Pi-calculus, a formal system for describing processes that communicate via channels. It provides an overview of the history and motivation for Pi-calculus, its basic elements like variables, channels, and processes, examples of how it can model processes and lambda calculus, and rules for reducing Pi-calculus expressions. Pi-calculus is used to describe concurrent and distributed systems formally and can describe processes that change over time through communication.

1. Formal Methods in
Software
Lecture 5. Pi-Calculus
Vlad Patryshev
SCU
2014 Prerequisites
λ-1, λ-2

2. This is Tier 2 of Modern Comp Sci

3. History: Hoare, CSP, 1978
The trouble is: it’s static in structure - no process creation allowed

4. What is π-calculus
• Describes processes developing in time
• Is conceptually similar to λ-calculus
• Is used to describe
o games
o security protocols (spi-calculus)
o biological and chemical processes
o business processes
• Is the base of modern concurrency libraries, like Scala Actors

5. Scala Actors, an implementation of π
class CustomerSupport extends Actor {
def act() {
while (true) {
receive {
case Stop =>
println("End of my sufferings")
exit()
case question:String => sender ! s"What do you mean, $question?!"
}
}
}
}

6. Elements of Pi
Notion Simplified Notation Milner Notation Meaning
variable x,y,... x,y,... Stores (points to) data; typeless
channel a,b,... a,b,... Used for communication
process (agent) P,Q,... P,Q,... Denotes a combination of elementary processes
write a!(x1,...xn) ā ⟨x1,...xn⟩ A process in which channel a outputs the values of
x (sends a message)
read a?(x1,...xn) a(x1,...xn) A process in which channel a reads a message with
values x1,...xn
new channel new(x1,...xn) ν(x1,...xn) Creates new names to be used within the scope
identifier A(x1,...)=P A(x1,...)=P given a process, give it a name

7. Operations on Processes
Operation Simplified Notation Milner Notation Meaning
sequence P.Q P.Q run process P, then process Q
parallel P|Q P|Q run processes P and Q in parallel
choice P+Q P+Q nondeterministically run either P or Q
match if x=y then P if x=y then P obvious (this op is optional)
mismatch if x≠y then P if x≠y then P obvious (this op is optional)
null process 0 0 does nothing, and ends
replication *(P)=P|*(P) !P unlimited replication of process P
reduction P → Q P → Q evaluation: P performs a step and becomes Q

8. Example
Printer = b?doc . Println(doc) . Printer
Server = a!b . Server
Client = a?p . p!doc
Life = Client | Server | Printer

9. Laws and Rules
First, a free variable is something that’s exposed to external world, while a
bound variable is hidden in a scope - so we are free to rename bound
variables, but we better not touch free variables.
Defining Free and Bound Names
• 0 has no bound or free names
• a?x - a is free, x is bound (it’s a new name to be used further down)
• new(x) - x is bound
• a!x - a and x are free
• A(x1,...xn)=P - x1,...xn are bound
• P.Q, P|Q, P+Q - free(P)∪free(Q), bound(P)∪bound(Q) (where’s the
rest?!)

10. Laws and Rules for Reduction
• fundamental rule (channels communication)
• alpha-conversion (like in lambda), and unfolding law
• monoid laws
• choice rule
• parallelization rule
• replication rule
• name binding rule
• scope extension laws

11. Laws and Rules for Reduction
• fundamental rule (channels communication, beta-reduction)
(x!z . P) | (x?y . Q) → P|(Q[y/z])
• alpha-conversion (like in lambda), and unfolding law
o P[x/y] ≡ P
o if A(x) = P, then A(y) = P[x/y]
• monoid laws
• choice rule
• parallelization rule
• replication rule
• name binding rule
• scope extension laws

12. Laws and Rules for Reduction
• fundamental rule (channels communication)
• alpha-conversion (like in lambda), and unfolding law
• monoid laws
| is a commutative monoid, 0 is a neutral element
+ is commutative and associative
• choice rule
o If P→Q, then (P+R) → (Q+R) (?)
• parallelism rule
o If P→Q, then (P|R) → (Q|R)
• replication rule
o If P→Q, then *(P) → Q|*(P) (this follows from definition)
• name binding rule

13. Laws and Rules for Reduction
• fundamental rule (channels communication)
• alpha-conversion (like in lambda), and unfolding law
• monoid laws
• choice rule
• parallelism rule
• replication rule
• name binding rule
If P→Q, then new(x).P → new(x).Q (new names don’t break it)
• scope extension laws
o new(x).0 = 0
o new(x).(P|Q)=P|(new(x).Q) if x∉fn(P)
o new(x).(P+Q)=P+(new(x).Q) if x∉fn(P)
o new(x).new(y).P = new(y).new(x).P

14. Can Model Lambda-Calculus
λ-expression π-agent on port p Meaning
M [M](p) Build an agent with a communication channel p
λx M p?x.p?q.[M](q) Given a channel p, obtain the value of x and the communication
channel q; call agent [M] on channel q
x x!p A variable, when used, just publishes its channel
M N new(a,b).(
([M](a))|
(a!b.a!f)|
*((b?c).[N](c))
Applying M to N means: create control channels a and b, and
launch in parallel:
● [M] on a (it will wait)
● pass b and f to M via channel a
● read channel b on y, start [N] which will work with channel c;
run it forever, we may need result more than once.

15. Modeling Lambda: Example
For M=λx x how will [M N] look? Can we reduce it to just [N]?
[(λx x) N](f) = new(a).new(b) . ([M](a) | (a!b.a!f) | *(b?c.[N](c)) ) =
new(a).new(b) . (a?x.a?y.x!y | (a!b.a!f) | *(b?c.[N](c)) ) →
new(a).new(b) . (a?y.b!y | (a!f) | *(b?c.[N](c)) ) →
new(a).new(b) . (b!f | 0 | *(b?c.[N](c)) ) →
new(a).new(b) . (b!f | *(b?c.[N](c)) ) →
new(a).new(b) . (b!f | b?c.[N](c)| *(b?c.[N](c)) ) →
new(a).new(b) . (0 | [N](f) | *(b?c.[N](c)) ) →
new(a).new(b) . ([N](f) | *(b?c.[N](c)) ) →
new(b) . ([N](f) | *(b?c.[N](c)) ) →
([N](f) | new(b). *(b@c.[N](c)) ) →
[N](f)

16. Modeling Lambda: Example
M=λa a, N=b // using (x!z).P | (x?y).Q ) → P|(Q[z/y])
[(λa a) b](p) = (new(q) . [M](q)) |
(new(y) . q!(y,p)) |
*((y?r) . [N](r)) =
(new(q) . q?(x,q’) . x!q’ |
(new(y) . q!(y,p)) |
*(y?r . z!r))) → /* reduces to */
(new(q) . (new(y) . y!p) |
*(y?r . z!r)) =
(new(q) . (new(y) . y!p) |
(y?r . z!r)) |
*(y?r . !z(r))) → /* reduces to */
(new(q) . (new(y) . z!p) |
*(?y(r) . z!r)) “=” /* nobody’s calling local channel y*/
(new(q) . (new(y) . z!p) “=” /* nobody uses q and y */
z!p =
[z](p)

17. References
http://scienceblogs.com/goodmath/2007/04/16/back-to-calculus-a-better-intr-1/
http://users.soe.ucsc.edu/~abadi/Papers/isss02.pdf
https://www.doc.ic.ac.uk/~pg/Concurrency/4pi.pdf
drona.csa.iisc.ernet.in/~deepakd/pav/crchandbook.ps
https://github.com/leithaus/SpecialK/blob/master/docs/presentations/Agents%20and%20agency%2
0in%20the%20Internet.pdf?raw=true
http://www.scala-lang.org/old/node/242
http://basics.sjtu.edu.cn/~yuxi/papers/lambda_in_pi.pdf
http://scala-programming-language.1934581.n4.nabble.com/scala-Actors-versus-processes-
td1993744.html - Greg Meredith discussing Pi and Scala Actors with Martin Odersky. Not much.
Wikipedia